Stratgie dencerclement connexe dans les graphes Pierre Fraigniaud



![Encerclement dans un graphe Stratégie d’encerclement (Parson. [GTC, 1976]). Suite de 3 opérations élémentaires Encerclement dans un graphe Stratégie d’encerclement (Parson. [GTC, 1976]). Suite de 3 opérations élémentaires](https://slidetodoc.com/presentation_image/ca59529c36b54d58f3d289352a513de2/image-4.jpg)













![Définitions : § Arête connexe e est dite connexe si G[T 1(e)] et G[T Définitions : § Arête connexe e est dite connexe si G[T 1(e)] et G[T](https://slidetodoc.com/presentation_image/ca59529c36b54d58f3d289352a513de2/image-30.jpg)











- Slides: 49

Stratégie d’encerclement connexe dans les graphes Pierre Fraigniaud, Nicolas Nisse LRI Orsay Séminaire du 12 novembre 2004

Encerclement dans les graphes n But Un groupe d’agents mobiles doit : - capturer un intrus dans un réseau ; - nettoyer un réseau contaminé ; Ø Utiliser le moins de ressources possibles. § Motivations Sécurité dans les réseaux informatiques ; Maintenance de réseaux de pipelines ; Opération de secours dans des souterrains. Réunion FRAGILE, Aussois, 23 mars 2005 2

Plan Stratégie d’encerclement Connexité Décomposition arborescente connexe Rapport cs(G)/s(G) Réunion FRAGILE, Aussois, 23 mars 2005 3
![Encerclement dans un graphe Stratégie dencerclement Parson GTC 1976 Suite de 3 opérations élémentaires Encerclement dans un graphe Stratégie d’encerclement (Parson. [GTC, 1976]). Suite de 3 opérations élémentaires](https://slidetodoc.com/presentation_image/ca59529c36b54d58f3d289352a513de2/image-4.jpg)
Encerclement dans un graphe Stratégie d’encerclement (Parson. [GTC, 1976]). Suite de 3 opérations élémentaires n n 1. 2. 3. n Placer un agent sur un sommet du graphe ; Déplacer un agent le long d’une arête ; Supprimer un agent d’un sommet du graphe. Résultant en le nettoyage du graphe Un agent nettoie une arête quand il la traverse ; Une arête reste propre si ses deux extrémités sont protégées. n On veut minimiser le nombre d’agents s(G), plus petit nombre d’agents nécessaire à une stratégie d’encerclement dans le graphe G. Réunion FRAGILE, Aussois, 23 mars 2005 4

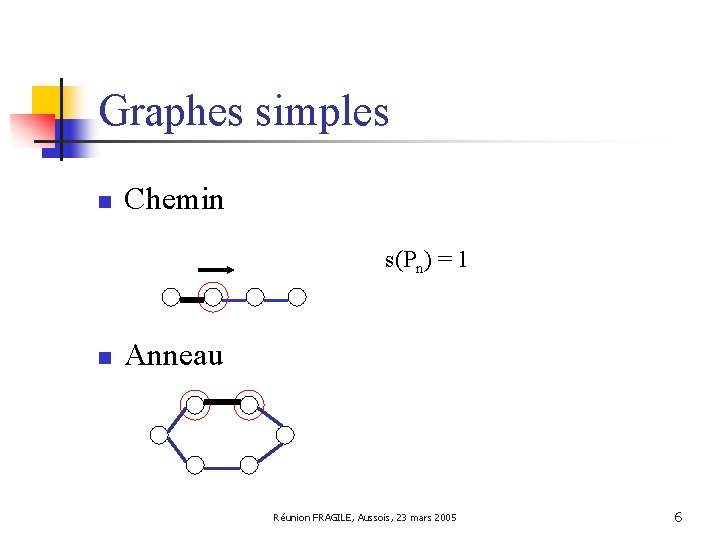
Graphes simples n Chemin Réunion FRAGILE, Aussois, 23 mars 2005 5

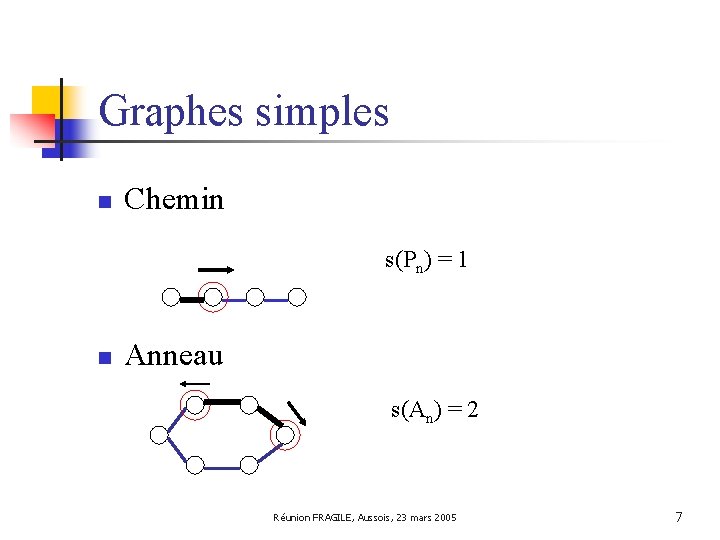
Graphes simples n Chemin s(Pn) = 1 n Anneau Réunion FRAGILE, Aussois, 23 mars 2005 6

Graphes simples n Chemin s(Pn) = 1 n Anneau s(An) = 2 Réunion FRAGILE, Aussois, 23 mars 2005 7

Stratégie d’encerclement monotone n Définition Une stratégie d’encerclement est monotone s’il n’y a pas de recontamination n Encerclement monotone ms(G), plus petit nombre d’agents nécessaire à une stratégie d’encerclement monotone dans le graphe G. Réunion FRAGILE, Aussois, 23 mars 2005 8

La recontamination n’aide pas n Pour tout graphe G, ms(G) = s(G). La. Paugh. Recontamination does not help to search a graph. [JACM, 1993] Bienstock et Seymour. Monotonicity in graph searching. [Jo. A, 1991] n s(G) ≤ k est un problème NP-complet Réunion FRAGILE, Aussois, 23 mars 2005 9

Décomposition arborescente (T, (Xv)v V(T) ) n n n un arbre et une famille de sommets de G ; 3 propriétés. Largeur de (T, X) = max{| Xv |-1 / v V(T)} Largeur d’arborescence de G, tw(G), est la largeur minimale parmi toutes les décompositions arborescentes de G. Décomposition linéaire (P, (Xv)v V(T) ), avec P un chemin n Largeur linéaire de G, pw(G). Réunion FRAGILE, Aussois, 23 mars 2005 10

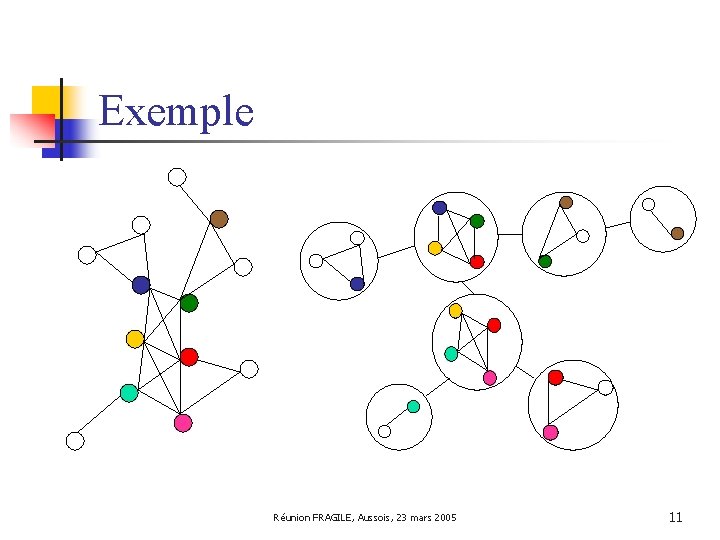
Exemple Réunion FRAGILE, Aussois, 23 mars 2005 11

Relations avec des paramètres “classiques” n Le fugitif est : Omniscient; Arbitrairement rapide. n Selon les variantes, le fugitif peut être : Visible => tw(G) ≤ s(G) ≤ tw(G)+1; Invisible => pw(G) ≤ s(G) ≤ pw(G)+1. Réunion FRAGILE, Aussois, 23 mars 2005 12

s(G) ≤ pw(G) + 2 Soit (X 1, X 2, …, Xi+1, …, Xr) une décomposition linéaire d’un graphe G de largeur pw(G). A l’étape i, le graphe induit par Uk<i Xk est nettoyé ; 1. Placer pw(G)+1 agents sur les sommets de Xi 2. Un agent supplémentaire nettoie les arêtes de Xi 3. Supprimer les agents des sommets de Xi/Xi+1 n X 1 Xi Xi+1 Réunion FRAGILE, Aussois, 23 mars 2005 Xr 13

pw(G) ≤ s(G) n Si (s 1, s 2, …, sr) est une stratégie d’encerclement monotone d’un graphe G, on construit une décomposition linéaire (X 1, X 2, …, Xi, …, Xr) telle que : Xi contient les sommets occupés, ainsi que l’arête éventuellement nettoyée lors de l’étape i. Réunion FRAGILE, Aussois, 23 mars 2005 14

Largeur linéaire ≈ encerclement n J. A. Ellis, I. H. Sudborough et J. S. Turner. The Vertex Separation and Search Number of a Graph. Inf. Comput. 1994. n N. G. Kinnersley. The Vertex Separation number of a graph equals its path-width. IPL. 1992. Pour tout graphe G de n sommets, pw(G) ≤ s(G) ≤ pw(G) + 1 Réunion FRAGILE, Aussois, 23 mars 2005 15

Plan Stratégie d’encerclement Connexité Décomposition arborescente connexe Rapport cs(G)/s(G) Réunion FRAGILE, Aussois, 23 mars 2005 16

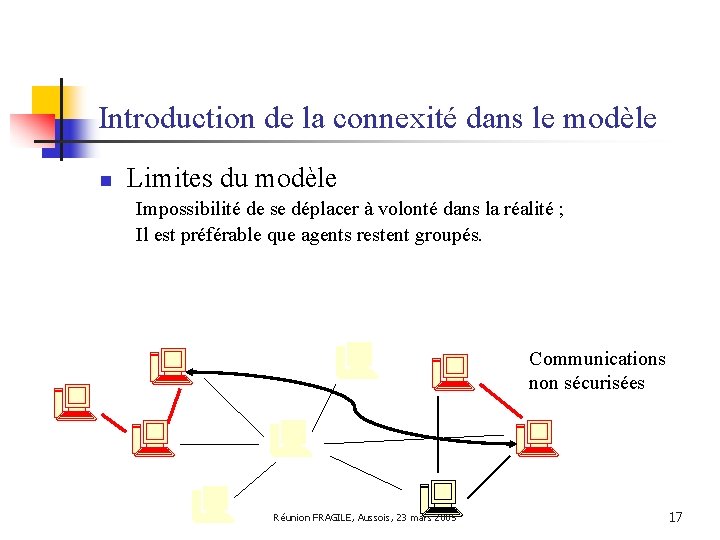
Introduction de la connexité dans le modèle n Limites du modèle Impossibilité de se déplacer à volonté dans la réalité ; Il est préférable que agents restent groupés. Communications non sécurisées Réunion FRAGILE, Aussois, 23 mars 2005 17

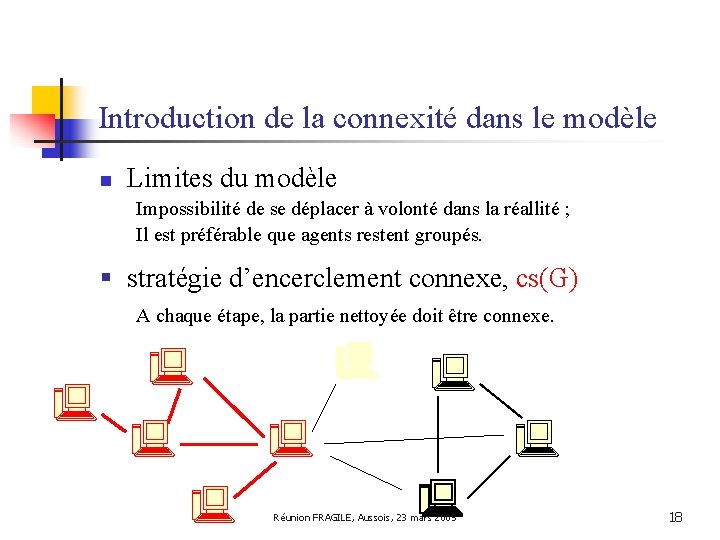
Introduction de la connexité dans le modèle n Limites du modèle Impossibilité de se déplacer à volonté dans la réallité ; Il est préférable que agents restent groupés. § stratégie d’encerclement connexe, cs(G) A chaque étape, la partie nettoyée doit être connexe. Réunion FRAGILE, Aussois, 23 mars 2005 18

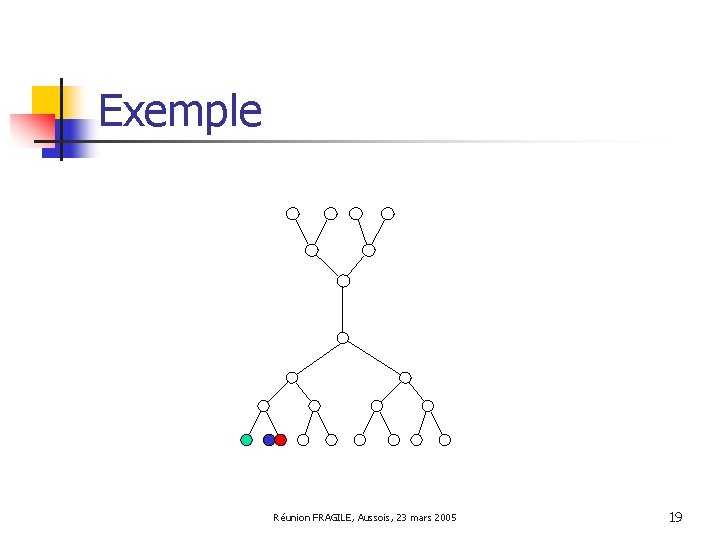
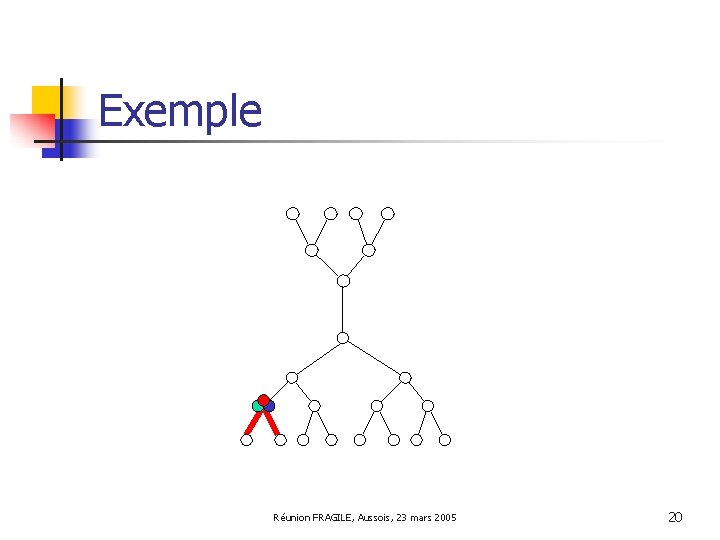
Exemple Réunion FRAGILE, Aussois, 23 mars 2005 19

Exemple Réunion FRAGILE, Aussois, 23 mars 2005 20

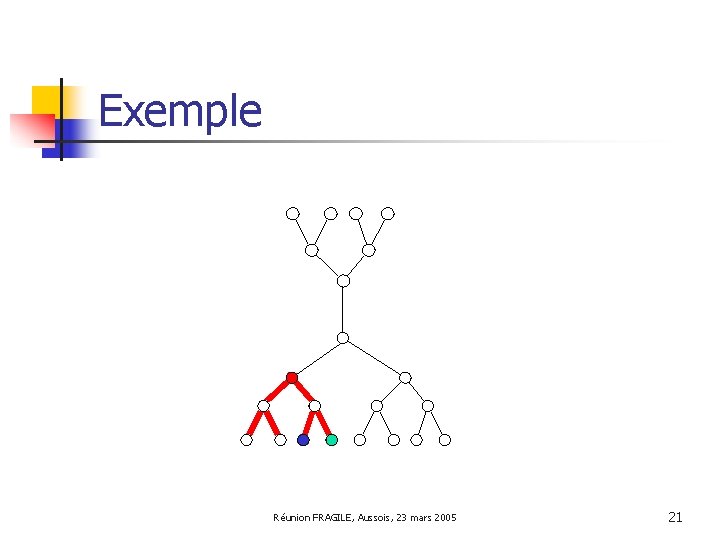
Exemple Réunion FRAGILE, Aussois, 23 mars 2005 21

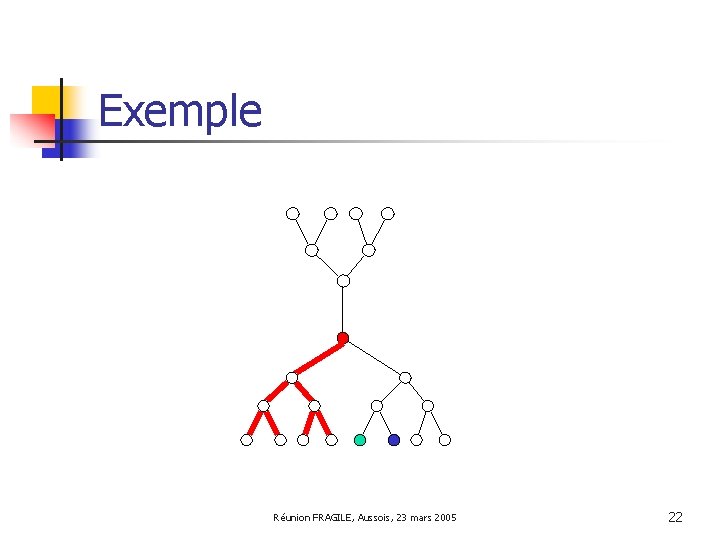
Exemple Réunion FRAGILE, Aussois, 23 mars 2005 22

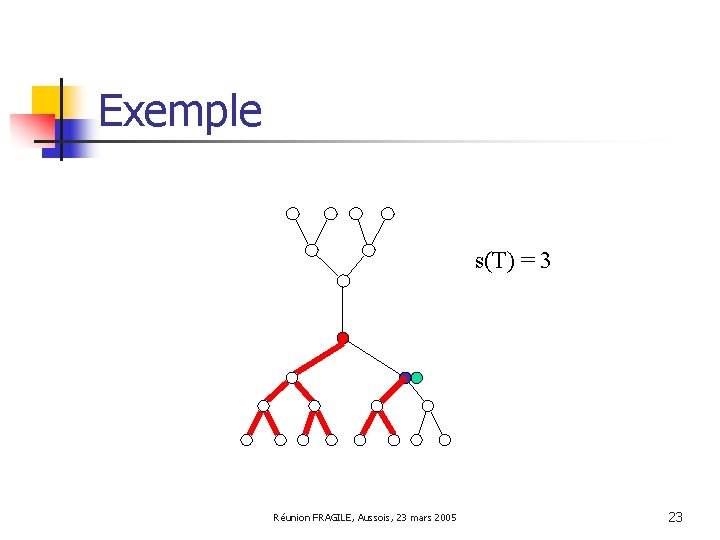
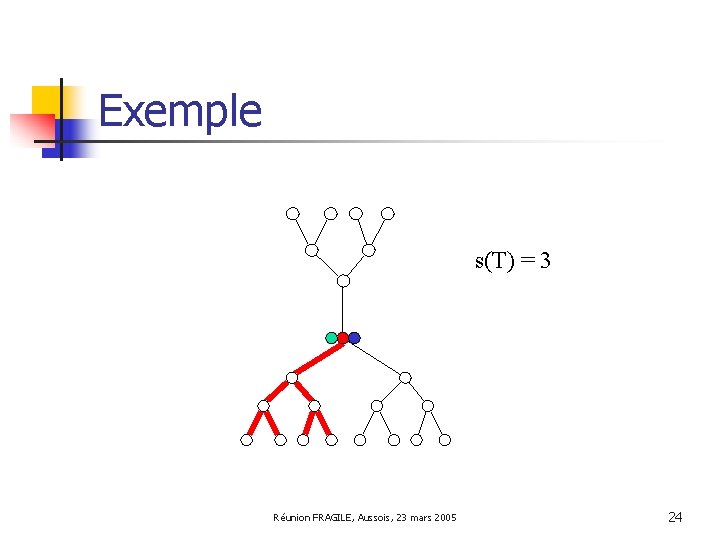
Exemple s(T) = 3 Réunion FRAGILE, Aussois, 23 mars 2005 23

Exemple s(T) = 3 Réunion FRAGILE, Aussois, 23 mars 2005 24

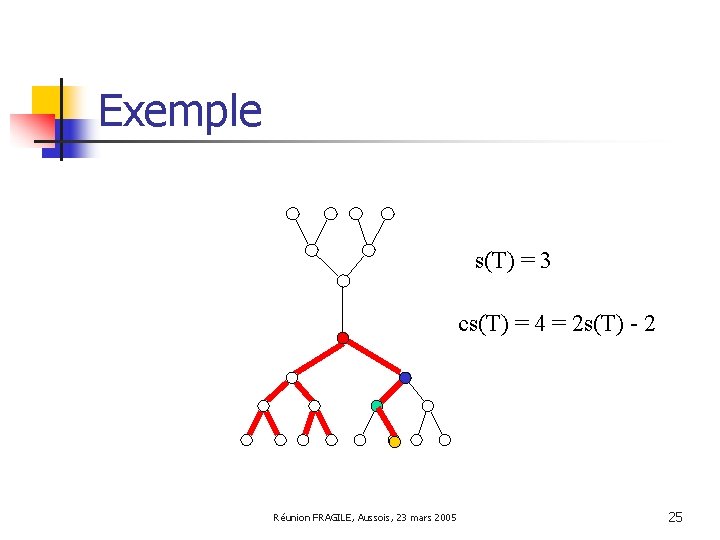
Exemple s(T) = 3 cs(T) = 4 = 2 s(T) - 2 Réunion FRAGILE, Aussois, 23 mars 2005 25

Connexe vs non connexe n L. Barriere, P. Fraigniaud, N. Santoro et D. Thilikos. Connected and Internal Graph Searching. WG, 2003. L’encerclement connexe cs(G) n’est pas invariant par mineur. n Daniel Dyer. Sweeping Graphs and Digraphs. [Thesis, 2004]. Dans le cas connexe, la recontamination aide. Réunion FRAGILE, Aussois, 23 mars 2005 26

Cas des arbres n L. Barriere, P. Flocchini, P. Fraigniaud et N. Santoro. Capture of an Intruder by Mobile Agents. SPAA, 2002. n n Algorithme linéaire calculant une stratégie d’encerclement connexe optimale et monotone dans le cas des arbres. L. Barriere, P. Fraigniaud, N. Santoro et D. Thilikos. Connected and Internal Graph Searching. WG, 2003. n Pour tout arbre T, s(T) ≤ cs(T) ≤ 2 s(T)-2 ; Réunion FRAGILE, Aussois, 23 mars 2005 27

Cas des graphes arbitraires n P. D. Seymour et R. Thomas. Call Routing and the Ratcatcher. Combinatorica, 14(2): 217 -241, 1994. n n F. Fomin, P. Fraigniaud et D. Thilikos [rapport technique, 2004] n n n Carving connexe ; Décomposition en branche connexe ; Algorithme polynomial constructif. F. Fomin, P. Fraigniaud et D. Thilikos [rapport technique, 2004] n Pour tout graphe connexe G, cs(G) ≤ s(G) (2+log 2 |E(G)|). Réunion FRAGILE, Aussois, 23 mars 2005 28

Plan Stratégie d’encerclement Connexité Décomposition arborescente connexe Rapport cs(G)/s(G) Réunion FRAGILE, Aussois, 23 mars 2005 29
![Définitions Arête connexe e est dite connexe si GT 1e et GT Définitions : § Arête connexe e est dite connexe si G[T 1(e)] et G[T](https://slidetodoc.com/presentation_image/ca59529c36b54d58f3d289352a513de2/image-30.jpg)
Définitions : § Arête connexe e est dite connexe si G[T 1(e)] et G[T 2(e)] sont des sous graphes connexes de G. e T 1(e) T 2(e) § Décomposition arborescente connexe (T, X) Toute arête de E(T) est connexe. § Largeur arborescente connexe, ctw(G). Réunion FRAGILE, Aussois, 23 mars 2005 30

Résultat (1) M. Golumbic, Algorithmic graph theory and perfect graphs. § Triangulation minimale tw(G) = min {w(H)/ H triangulation minimale de G} § Arbre de cliques A. Parra and P. Scheffler, Characterizations and algorithmic applications of chordal graphs embedding. Réunion FRAGILE, Aussois, 23 mars 2005 31

Résultat (1) Théorème : § Pour tout graphe connexe G, ctw(G) = tw(G). Preuve constructive : § Algorithme polynomial qui, étant donnée une décomposition arborescente de largeur k de G, retourne une décomposition arborescente connexe de largeur ≤ k de G. Réunion FRAGILE, Aussois, 23 mars 2005 32

Définition n n Décomposition arborescente enraciné en un sommet u. Arête sous-connexe Une arête e = (w, v) où w est le père de v, est sous-connexe si : G[T(v)] est un sous graphe connexe de G. u w v e n (T, X) sous connexe en v V(T) - G[T(v)] est un sous graphe connexe de G ; toute arête de T(v) est sous connexe. T(v) Réunion FRAGILE, Aussois, 23 mars 2005 33

Algorithme (1) n Entrée : n n (Tu, X) une décomposition arborescente de largeur k de G. 2 phases n n Montée : rend la décomposition sous-connexe Descente : rend la décomposition connexe Réunion FRAGILE, Aussois, 23 mars 2005 34

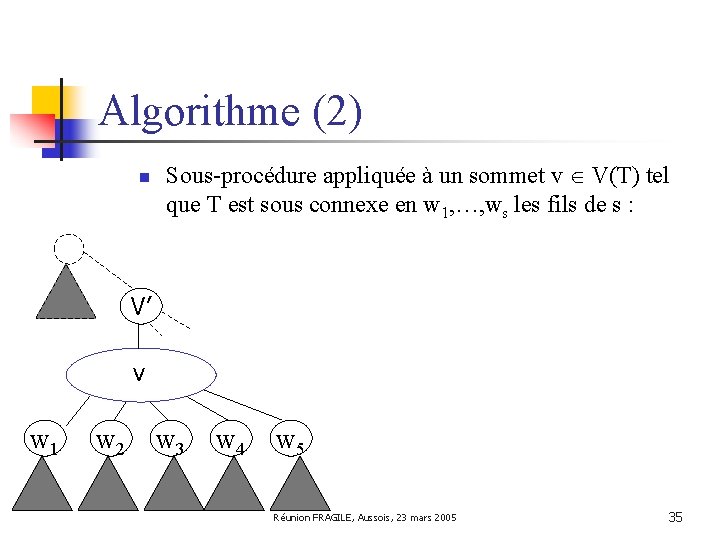
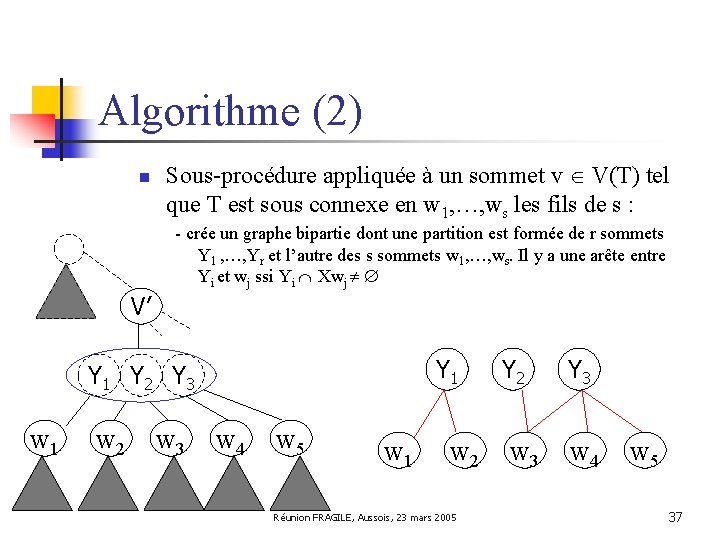
Algorithme (2) n Sous-procédure appliquée à un sommet v V(T) tel que T est sous connexe en w 1, …, ws les fils de s : V’ v w 1 w 2 w 3 w 4 w 5 Réunion FRAGILE, Aussois, 23 mars 2005 35

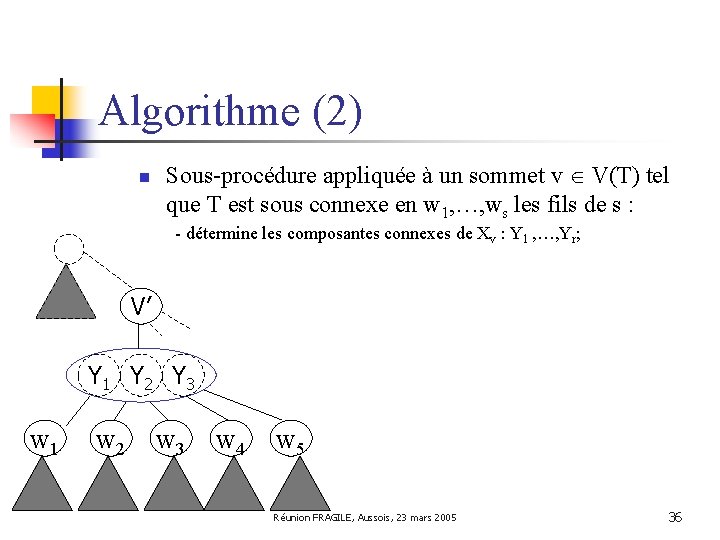
Algorithme (2) n Sous-procédure appliquée à un sommet v V(T) tel que T est sous connexe en w 1, …, ws les fils de s : - détermine les composantes connexes de Xv : Y 1 , …, Yr; V’ Y 1 Y 2 Y 3 w 1 w 2 w 3 w 4 w 5 Réunion FRAGILE, Aussois, 23 mars 2005 36

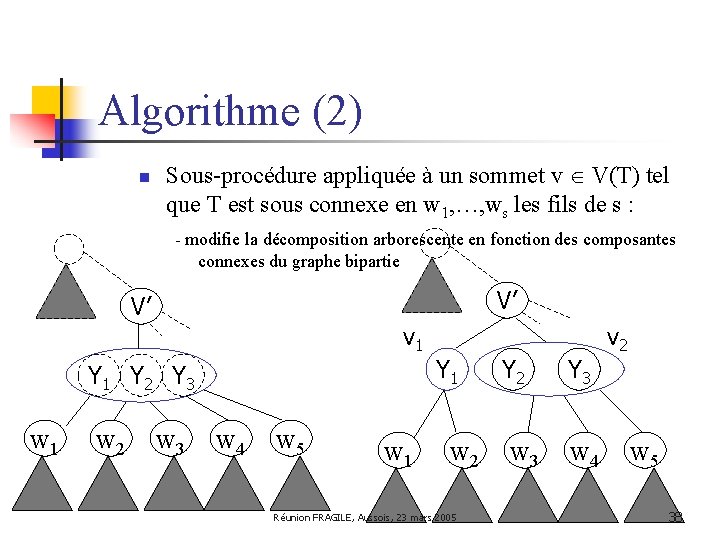
Algorithme (2) n Sous-procédure appliquée à un sommet v V(T) tel que T est sous connexe en w 1, …, ws les fils de s : - crée un graphe bipartie dont une partition est formée de r sommets Y 1 , …, Yr et l’autre des s sommets w 1, …, ws. Il y a une arête entre Yi et wj ssi Yi Xwj V’ Y 1 Y 2 Y 3 w 1 w 2 w 3 w 4 w 5 w 1 w 2 Réunion FRAGILE, Aussois, 23 mars 2005 Y 2 w 3 Y 3 w 4 w 5 37

Algorithme (2) n Sous-procédure appliquée à un sommet v V(T) tel que T est sous connexe en w 1, …, ws les fils de s : - modifie la décomposition arborescente en fonction des composantes connexes du graphe bipartie V’ V’ v 1 Y 2 Y 3 w 1 w 2 w 3 w 4 w 5 w 1 Y 1 w 2 Réunion FRAGILE, Aussois, 23 mars 2005 Y 2 w 3 Y 3 w 4 v 2 w 5 38

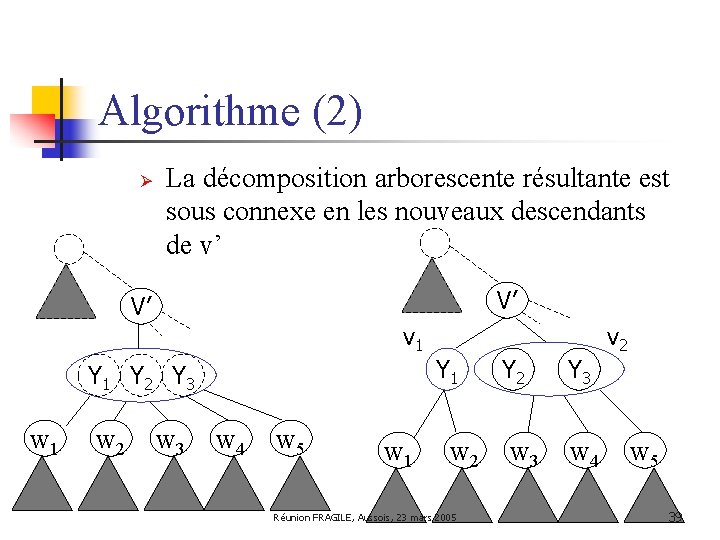
Algorithme (2) Ø La décomposition arborescente résultante est sous connexe en les nouveaux descendants de v’ V’ V’ v 1 Y 2 Y 3 w 1 w 2 w 3 w 4 w 5 w 1 Y 1 w 2 Réunion FRAGILE, Aussois, 23 mars 2005 Y 2 w 3 Y 3 w 4 v 2 w 5 39

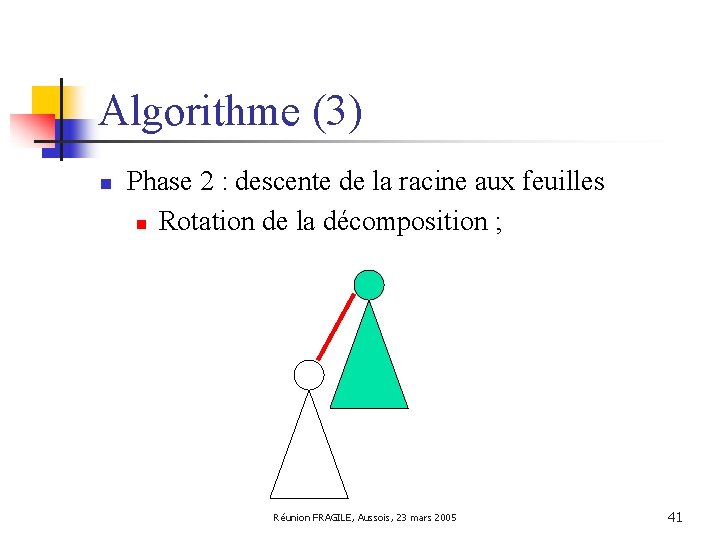
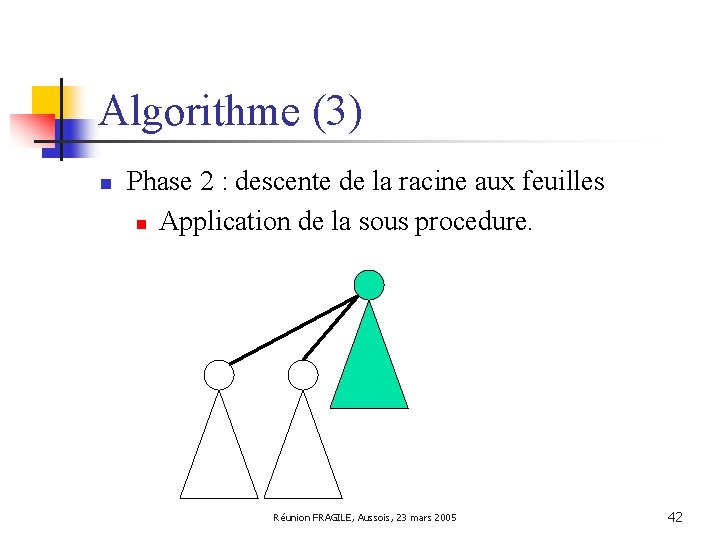
Algorithme (3) n Phase 2 : descente de la racine aux feuilles n n Entrée : décomposition arborescente sous-connexe ; Il reste des arêtes qui font défaut à la connexité ; Réunion FRAGILE, Aussois, 23 mars 2005 40

Algorithme (3) n Phase 2 : descente de la racine aux feuilles n Rotation de la décomposition ; Réunion FRAGILE, Aussois, 23 mars 2005 41

Algorithme (3) n Phase 2 : descente de la racine aux feuilles n Application de la sous procedure. Réunion FRAGILE, Aussois, 23 mars 2005 42

Complexité n Algorithme en O(N. k 3) avec N=|V(G)| et k la largeur de la décomposition arborescente en entrée n V. Bouchitté, D. Kratsch, H. Muller and I. Todinca. On treewidth approximations. Il existe un algorithme polynomial qui calcule une décomposition arborescente de largeur au plus tw(G). log tw(G). Réunion FRAGILE, Aussois, 23 mars 2005 43

Plan Stratégie d’encerclement Connexité Décomposition arborescente connexe Rapport cs(G)/s(G) Réunion FRAGILE, Aussois, 23 mars 2005 44

Résultat (2) Théorème : § Pour tout graphe connexe G, cs(G) ≤ s(G) (2+log 2 |V(G)|). Preuve constructive : § Algorithme construisant une stratégie d’encerclement connexe de G utilisant au plus tw(G). log |V(G)| agents. Réunion FRAGILE, Aussois, 23 mars 2005 45

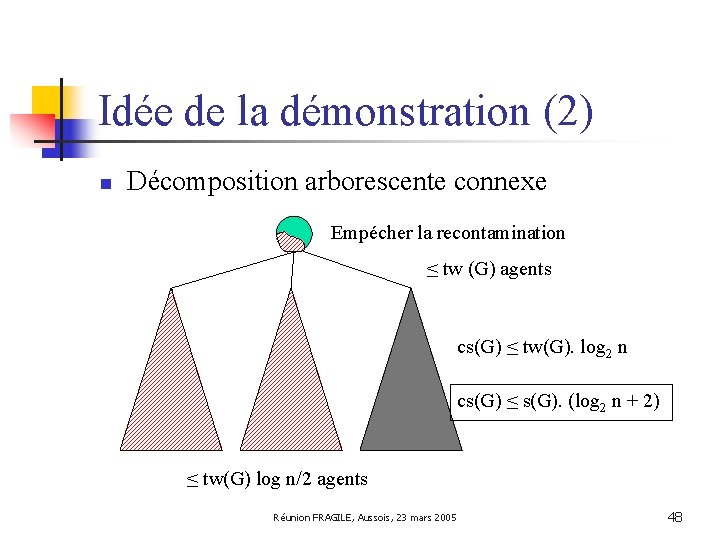
Idée de la démonstration (1) n n n T 1 Démonstration par induction sur |V(G)|. N. Robertson et P. D. Seymour. Graph Minors II. Algorithmic Aspects of Tree-Width. J. of Alg 7, 1986. 2 cas : pour toute décomposition arborescente d’un graphe G de n sommets, il existe 1 ou 2 sommets tels que : Ø Pour tout 1 ≤ j ≤ r, |G[Tj]| ≤ n/2 Ti Tr T T T 1 Réunion FRAGILE, Aussois, i 23 mars 2005 i+1 Tr 46

Idée de la démonstration (2) n Décomposition arborescente connexe Empécher la recontamination ≤ tw (G) agents ≤ tw(G) log n/2 agents Réunion FRAGILE, Aussois, 23 mars 2005 47

Idée de la démonstration (2) n Décomposition arborescente connexe Empécher la recontamination ≤ tw (G) agents cs(G) ≤ tw(G). log 2 n cs(G) ≤ s(G). (log 2 n + 2) ≤ tw(G) log n/2 agents Réunion FRAGILE, Aussois, 23 mars 2005 48

Conclusions n Résultats n n n connexité inhérente à la décomposition arborescente ; nouvelle borne supérieure pour cs(G)/s(G) ; Perspectives n n Amélioration de la borne cs/s ; généralisation aux graphes q-connexes ; algorithmes répartis ; algorithmes paramétrés. Réunion FRAGILE, Aussois, 23 mars 2005 49
 Pierre fraigniaud
Pierre fraigniaud L'auteur de la ficelle
L'auteur de la ficelle Sommes nous surs
Sommes nous surs Observe les membres de la famille de pierre
Observe les membres de la famille de pierre Les instructions de la classe
Les instructions de la classe Les caractéristiques du début d'un conte
Les caractéristiques du début d'un conte Nous sommes les étoiles dans le ciel d'abraham paroles
Nous sommes les étoiles dans le ciel d'abraham paroles Mécanisme intervenant dans les échanges cellulaires
Mécanisme intervenant dans les échanges cellulaires Transmission ciblées
Transmission ciblées Les professeurs 1 of 1 dans la salle de classe.
Les professeurs 1 of 1 dans la salle de classe. Zone chaude zone froide magasin
Zone chaude zone froide magasin Groupe verbal
Groupe verbal Axes de lecture le dernier jour d'un condamné
Axes de lecture le dernier jour d'un condamné Fleuve des enfers
Fleuve des enfers Remerciement rapport de stage enseignement
Remerciement rapport de stage enseignement Exemple texte d'opinion
Exemple texte d'opinion Le guide de la parfaite femme au foyer dans les années 50
Le guide de la parfaite femme au foyer dans les années 50 Haribo marque allemande
Haribo marque allemande Quel beau nom que celui d'emmanuel
Quel beau nom que celui d'emmanuel Organisateurs textuels conclusion
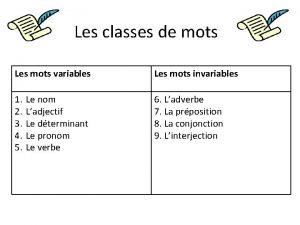
Organisateurs textuels conclusion Classes de mots variables
Classes de mots variables Parts d'una flor
Parts d'una flor Les voitures les plus rapides du monde
Les voitures les plus rapides du monde Les avantages et les inconvénients de la matrice adl
Les avantages et les inconvénients de la matrice adl Je moi tu toi
Je moi tu toi Cestbeaulavie
Cestbeaulavie Preactionneurs
Preactionneurs Trouvez les réponses. écrivez-les en chiffres (numbers).
Trouvez les réponses. écrivez-les en chiffres (numbers). Les lettres et les sons
Les lettres et les sons Tu aimes manger
Tu aimes manger Part de la planta en la fulla s'uneix a la tija
Part de la planta en la fulla s'uneix a la tija Les arguments pour tous les sujets
Les arguments pour tous les sujets Grand corps malade histoire d'amour
Grand corps malade histoire d'amour Les trois obstacles et les quatre démons
Les trois obstacles et les quatre démons Les 10 volcans les plus dangereux du monde
Les 10 volcans les plus dangereux du monde Les mots qu'on ne dit pas sont les fleurs du silence
Les mots qu'on ne dit pas sont les fleurs du silence Les mots variable
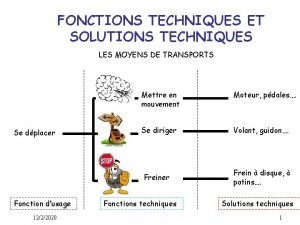
Les mots variable Les fonctions techniques et les solutions techniques
Les fonctions techniques et les solutions techniques En quittant cette terre
En quittant cette terre Se yon bel pale kristal chant d'esperance
Se yon bel pale kristal chant d'esperance Les constellations les plus connues
Les constellations les plus connues La pierre du tombeau a été roulée alléluia
La pierre du tombeau a été roulée alléluia International pierre de coubertin committee
International pierre de coubertin committee Cest pourquoi
Cest pourquoi Rsultat
Rsultat Bourdieu, habitus nedir
Bourdieu, habitus nedir Pierre desproges
Pierre desproges Pierre robin
Pierre robin Lycée marie curie versailles bts
Lycée marie curie versailles bts Jean pierre landau
Jean pierre landau