Quapprendon dans ce chapitre Questce quune composante connexe

Qu’apprend-on dans ce chapitre • Qu’est-ce qu’une composante connexe et comment calcule-t-on une distance discrère ; • les opérateurs de Morphologie Mathématique : • de base: érosion, dilatation, ouverture, fermeture ; • les transformées en tout ou rien ; • Qu’est ce que la reconstruction géodésique binaire et à quoi sert-elle ; • Qu’est qu’un squelette et comment on le calcule ;

Notions préliminaires de géométrie discrète • Topologie 2 D discrète : nombre de composantes connexes, de trous, représentation hiérarchique des objets. • Distances discrètes : Relations ensemblistes entre les parties d’un objet dimension (e. g. rayon) des composantes connexes, distance entre les objets.

Voisinage élémentaire et entourage • Image discrète = graphe • Connexité trame carrée trame hexagonale • Chemin sur le graphe = succession de nœuds du graphe joints par des arcs chemin 4 -connexe : chemin 8 -connexe : • Théorème de Jordan : toute courbe simple fermée sépare l’espace en 2 composantes : l’intérieur et l’extérieur de la courbe. Cas de la trame carrée : tout chemin 4 -connexe (resp. 8 -connexe) simple fermé (Ai=Aj i=j et Ai voisin de Aj |i-j|=1[n]) sépare l’espace en 2 composantes 8 -connexes (resp. 4 -connexes)

Exemple : nombre d’Euler • Nombre d’Euler = différence entre le nombre composantes connexes et le nombre de trous (attention à la dualité des connexités). Soit : s=nb singletons, a=nb couples ligne ou colonne, d=nb couples diagonaux, t=nb trinômes, q=nb quadrinômes, alors en 4 -connexité E=s-a+q en 8 -connexité E=s-a-d+t-q Ex: • Cas 4 -connexe : nombre composantes 4 -connexes = 3 nombre de trous (8 -connexes) = 1 E 4=2 • Cas 8 -connexe : nombre composantes 8 -connexes = 1 nombre de trous (4 -connexes) = 2 E 8=-1 s=16, a=14, d=13, t=10, q=0 En 4 -connexité E 4=s-a+q=2 En 8 -connexité E 8=s-a-d+t-q=-1

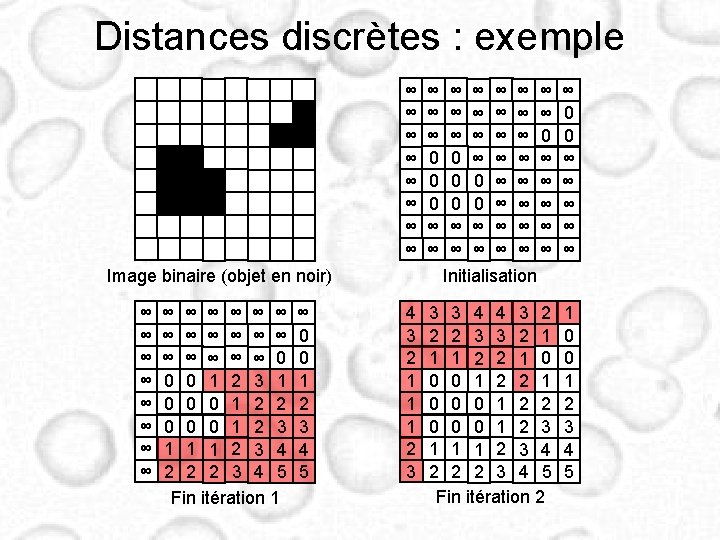
Distances discrètes (I) • Distance à 1 objet minimum des distances euclidiennes (approximées) aux points de l’objet • Propagation de distances locales • Distances définies à partir d’un ensemble de vecteurs de déplacement • Utilisation de masques 1 1 0 1 • Exemple : 1 11 1 4 3 4 1 0 1 3 0 3 1 1 1 4 3 4 11 11 11 7 5 0 5 7 11 11

Distances discrètes (II) • Partition du masque en 2 sous-masques g 1 et g 2 causaux UL LR et LR UL • Algorithme de calcul séquentiel 1) Poser 2) f 0 image / points de l’objet 0 et les autres + 3) pour k=1, 2 si k=1, balayer l’image dans le sens UL LR si k=2, balayer l’image dans le sens LR UL 4) image des distances f 2 4 3 0 3 4

Distances discrètes : exemple ∞ ∞ ∞ 0 0 0 ∞ ∞ ∞ ∞ 0 0 ∞ ∞ ∞ ∞ ∞ Initialisation ∞ 0 0 ∞ ∞ ∞ 4 3 2 1 1 1 2 3 3 3 4 4 3 2 2 2 3 3 2 1 1 1 2 2 1 0 0 0 1 2 2 0 0 0 1 2 3 1 1 1 2 3 4 2 2 2 3 4 5 Fin itération 2 1 0 0 1 2 3 4 5 Image binaire (objet en noir) ∞ ∞ ∞ ∞ ∞ ∞ ∞ 0 0 0 1 2 3 1 0 0 0 1 2 2 0 0 0 1 2 3 1 1 1 2 3 4 2 2 2 3 4 5 Fin itération 1 ∞ 0 0 1 2 3 4 5

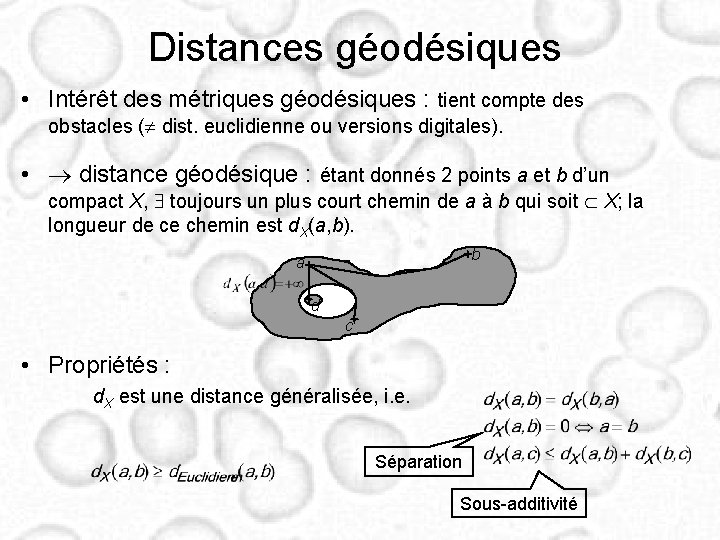
Distances géodésiques • Intérêt des métriques géodésiques : tient compte des obstacles ( dist. euclidienne ou versions digitales). • distance géodésique : étant donnés 2 points a et b d’un compact X, toujours un plus court chemin de a à b qui soit X; la longueur de ce chemin est d. X(a, b). b a d c • Propriétés : d. X est une distance généralisée, i. e. Séparation Sous-additivité

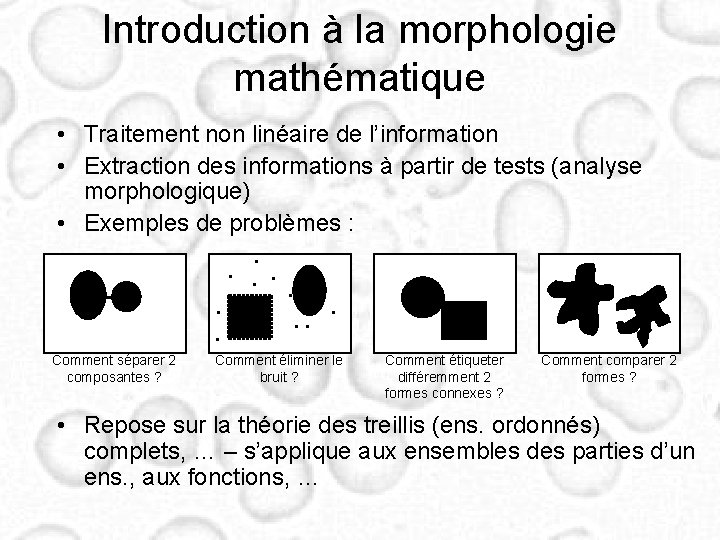
Introduction à la morphologie mathématique • Traitement non linéaire de l’information • Extraction des informations à partir de tests (analyse morphologique) • Exemples de problèmes : Comment séparer 2 composantes ? Comment éliminer le bruit ? Comment étiqueter différemment 2 formes connexes ? Comment comparer 2 formes ? • Repose sur la théorie des treillis (ens. ordonnés) complets, … – s’applique aux ensembles des parties d’un ens. , aux fonctions, …

• Définition: 1 treillis complet est 1 ensemble ordonné (E, ) tel que toute partie de E admette 1 borne supérieure et 1 borne inférieure : réflexive ( x E, x x), plus grand des minorants plus petit des majorants antisymétrique ( (x, y) E 2, x y et y x x=y), transitive ( (x, y, z) E 3, x y et y z x z ) • Treillis de l’ensemble des parties d’ 1 ensemble S : éléments parties de S relation d’ordre inclusion borne supérieure union borne inférieure intersection involution complémentaire

Opérateurs de MM : fondements mathématiques • principes fondamentaux – Compatibilité avec les translations Indépendance par rapport à l’origine de l’espace: t, y(f+t)=y(f)+t – Compatibilité avec les homothéties Indépendance par rapport au paramètre d’échelle: l, y(lf)=ly(f) – Localité E’ borné, E borné / y(f) E’=y(f E) E’ • propriétés – Croissance A, B A B y(A) y(B) – Extensivité / anti-extensivité – Idempotence – Dualité y(y(. ))=y(. ) y et f duales : Extensivité: A, A y(A)

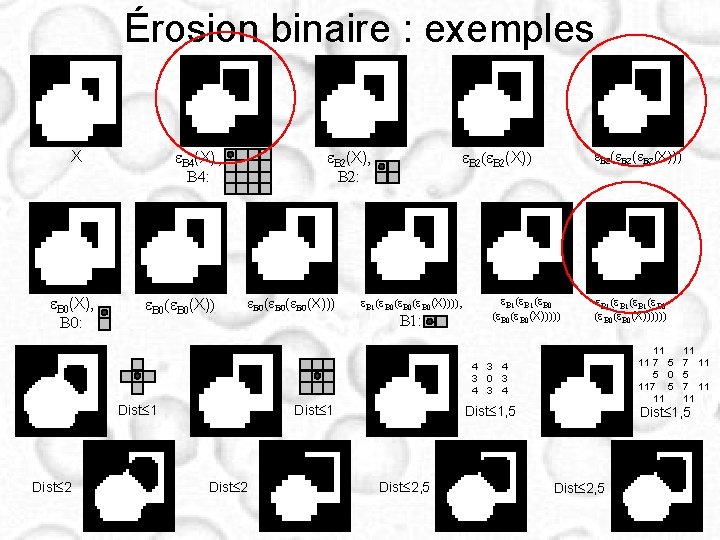
Erosion / dilatation : définitions (1) • Élément structurant B relations de l’objet X avec l’élément (taille, forme données) • Addition de Minkowski : Union des translatés de X par chaque ‘point’ de B propriétés : commutative, associative, croissante, élément neutre • Soustraction de Minkowski : Ө Intersection des translatés de X par chaque point de B propriétés : non commutative, associative, croissante, élément neutre

Erosion / dilatation : définitions (2) • Dilatation (binaire) : lieu géométrique des points x tels que Bx intersecte X • Erosion (binaire) : lieu géométrique des points x tels que Bx soit inclus dans X • dualité érosion / dilatation

Erosion / dilatation : algorithmes (1) • Cas général (binaire) : – En chaque pixel z de l’image examiner la relation entre l’élément struct. Bz et l’objet X – Dilatation: pour i [1, #lignes] // boucle sur les lignes pour j [1, #colonnes] { // boucle sur les colonnes initializer y à 0 pour i’ [i. Bmin, i. Bmax] // origine de B en 0 B inclus dans [i. Bmin, i. Bmax] [j. Bmin, j. Bmax] pour j’ [j. Bmin, j. Bmax] si (y nul et ima(i+i’, j+j’) non nul et B(i’, j’) non nul) alors y 1 ima_dilate(i, j) y } – Erosion: pour i [1, #lignes] // boucle sur les lignes pour j [1, #colonnes] { // boucle sur les colonnes initializer y à 1 pour i’ [i. Bmin, i. Bmax] // origine de B en 0 B inclus dans [i. Bmin, i. Bmax] [j. Bmin, j. Bmax] pour j’ [j. Bmin, j. Bmax] si (y non nul et ima(i+i’, j+j’) nul et B(i’, j’) non nul) alors y 0 ima_erode(i, j) y }

Erosion / dilatation : algorithmes (2) • Exploitation de l’associativité de la dilatation / érosion – Cas d’un élément B qui est le résultat de l’addition de Minkowski de et avec B 1 (B à la taille élémentaire) : • Itérer la dilatation (érosion) par B 1 – Cas d’un élément convexe : • Dilatations (érosions) successives par 2 segments • Cas d’un élément structurant ‘boule’ : – Seuillage de la transformée en distance de l’image binaire ou de son complémentaire

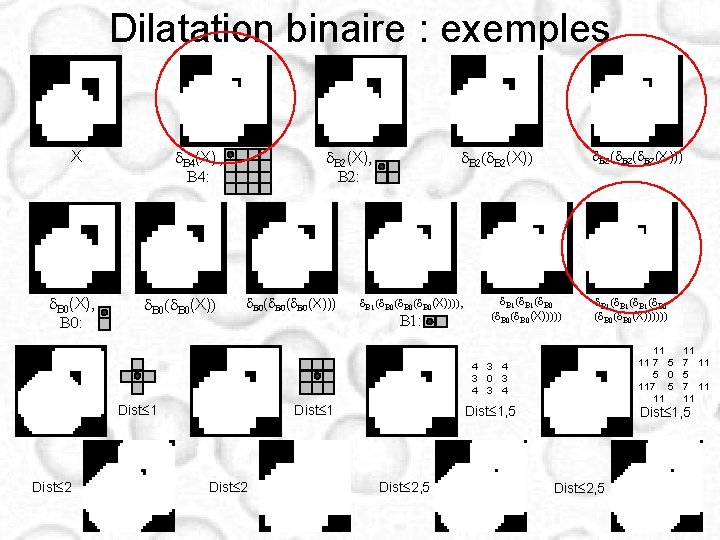
Dilatation binaire : exemples d. B 0(X), B 0: d. B 2(X), B 2: d. B 4(X) , B 4: X d. B 0(X)) d. B 0(d. B 0(X))) d. B 2(X)) d. B 1(d. B 0(d. B 0(X)))), B 1: d. B 2(d. B 2(X))) d. B 1(d. B 0 (d. B 0(X)))))) 11 11 11 7 5 7 11 5 0 5 117 5 7 11 11 11 4 3 0 3 4 Dist 1 Dist 2 Dist 1, 5 Dist 2, 5

Érosion binaire : exemples e. B 0(X), B 0: e. B 2(X), B 2: e. B 4(X) , B 4: X e. B 0(X)) e. B 0(e. B 0(X))) e. B 2(X)) e. B 1(e. B 0(e. B 0(X)))), B 1: e. B 2(e. B 2(X))) e. B 1(e. B 0 (e. B 0(X)))))) 11 11 11 7 5 7 11 5 0 5 117 5 7 11 11 11 4 3 0 3 4 Dist 1 Dist 2 Dist 1, 5 Dist 2, 5

Erosion / dilatation : propriétés (1) • Croissance par rapport à X En effet : • Extensivité / anti-extensivité (si centre de B inclus dans B) • Croissance / décroissance par rapport à B En effet :

Erosion / dilatation : propriétés (2) • Commutations en effet : • Adjonction en effet : La partie de Bz qui n’intersecte pas avec X est dans le complémentaire de Bz’ quand on se restreint à Bz Bz’ on ‘est dans’ X

Erosion / dilatation : exemples illustrant les propriétés • Soit les éléments structurants : X=d. B 1 B 2(X) X=e. B 1 B 2(X) d. B 1(X) e. B 1(X) et · B 1 d. B 2(X) e. B 2(X) B 2 · d. B 1(X) d. B 2(X) e. B 1(X) e. B 2(X)

Ouverture / fermeture binaires • Définition • Exemples e 5(X) e 15(X) binarisation X-e 5(X) X-e 15(X) g 15(X) X-g 15(X)

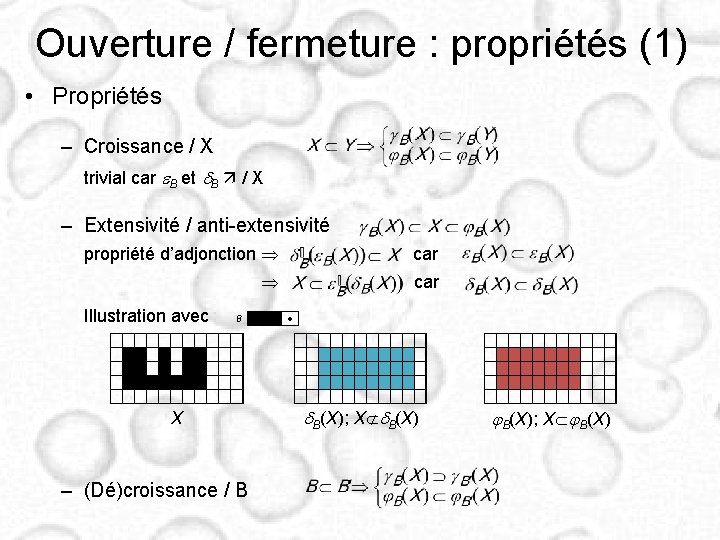
Ouverture / fermeture : propriétés (1) • Propriétés – Croissance / X trivial car e. B et d. B / X – Extensivité / anti-extensivité propriété d’adjonction car Illustration avec B X – (Dé)croissance / B · d. B(X); X d. B(X) j. B(X); X j. B(X)

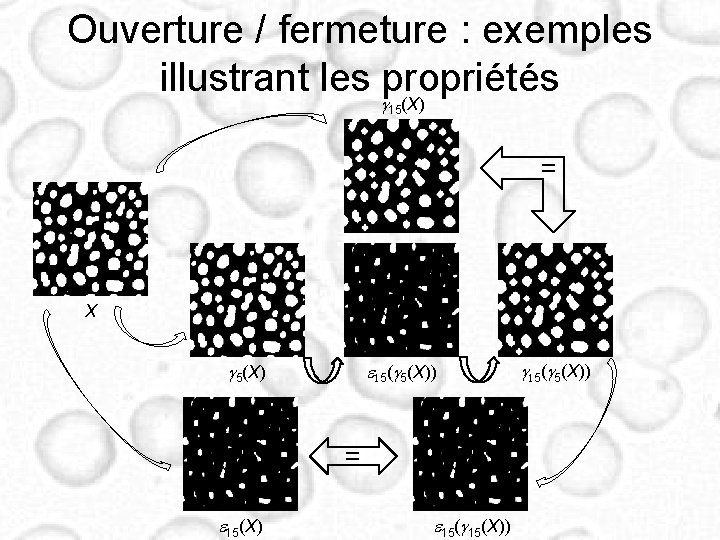
Ouverture / fermeture : propriétés – Idempotence – – Min-max : L’ouverture de X est le plus petit X’ de même érodé que X La fermeture de X est le plus grand X’ de même dilaté que X

Ouverture / fermeture : exemples illustrant les gpropriétés (X) 15 = X e 15(g 5(X)) g 5(X) = e 15(X) e 15(g 15(X)) g 15(g 5(X))

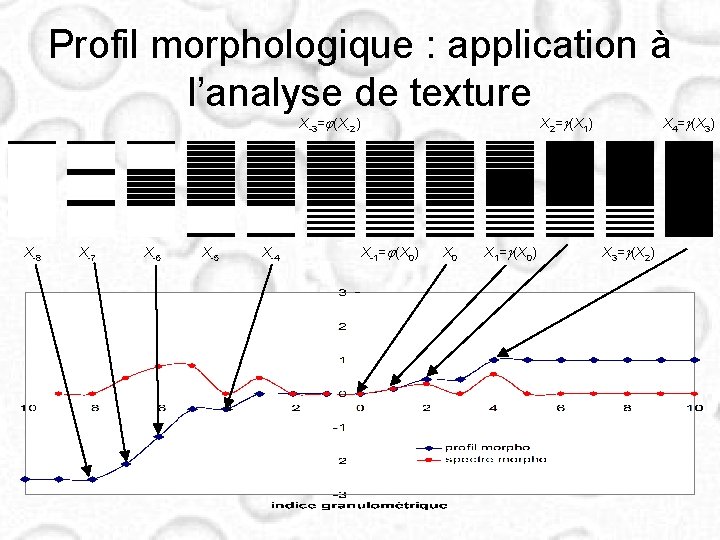
Profil morphologique : définition • (gl)l≥ 0 une ‘granulométrie’ et (jl)l≥ 0 l’antigranulométrie associée (gl)l 0 / 0 l l’ gl’gl=glgl’=gl’ • Fonction de distribution granulométrique m mesure bornée sur le treillis (e. g. aire #pixels) Xl = gl(X) et X-l = jl(X) FX(l)=1 -m(Xl)/m(X 0) • Spectre granulométrique f. X(l)= F’X(l) (dérivée de FX)

Profil morphologique : application à l’analyse de texture X-3=j(X-2) X-8 X-7 X-6 X-5 X-4 X 2=g(X 1) X-1=j(X 0) X 0 X 1=g(X 0) X 4=g(X 3) X 3=g(X 2)

Dilatation / Erosion géodésique binaire • Boules géodésiques • Quand l , les boules géodésiques progressent comme le front d’une onde émise depuis z dans milieu l X Dilatation géodésique deletaille de Y dans X (Y Bl) X • Erosion géodésique X Y 1 e. X(Y 1) Y 2 e(Y 2) X

Reconstruction géodésique binaire • Principe : à partir de marqueurs d’une composante connexe, on reconstruit toute la composante • Méthode : dilatation géodésique dans X • Algorithme – Initialisation de la pile avec les pixels de X Y – Tant qu’il reste des éléments dans la pile : • Extraire un élément (pixel) de la pile • Le traiter – Mise à 1 dans l’image résultat binaire – Calcul de ses voisins (dilatation par B) • Ajout dans la pile (si nécessaire) des voisins situés dans X

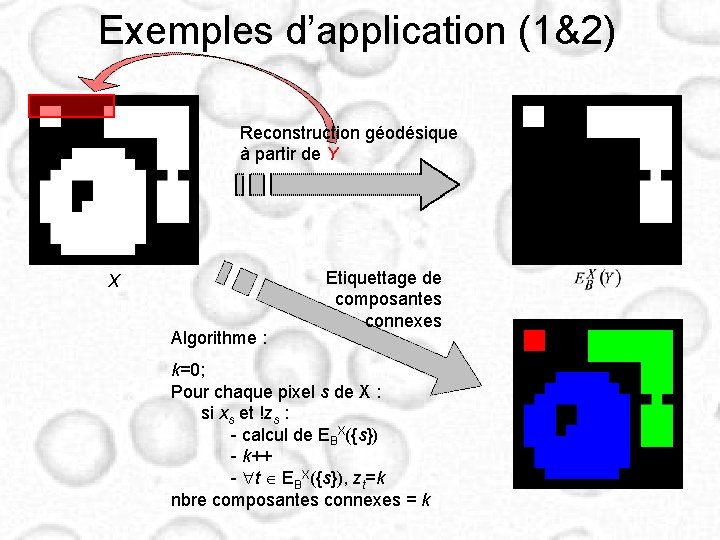
Exemples d’application (1&2) Reconstruction géodésique à partir de Y X Algorithme : Etiquettage de composantes connexes k=0; Pour chaque pixel s de X : si xs et !zs : - calcul de EBX({s}) - k++ - t EBX({s}), zt=k nbre composantes connexes = k

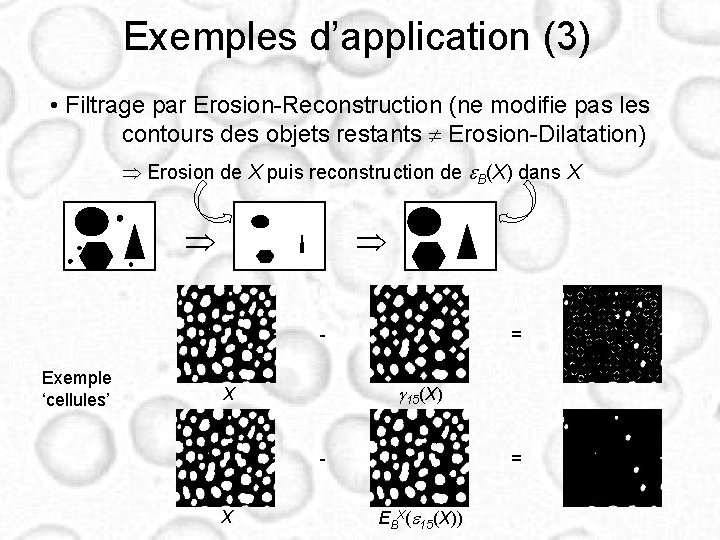
Exemples d’application (3) • Filtrage par Erosion-Reconstruction (ne modifie pas les contours des objets restants Erosion-Dilatation) Erosion de X puis reconstruction de e. B(X) dans X - Exemple ‘cellules’ = g 15(X) X X = EBX(e 15(X))

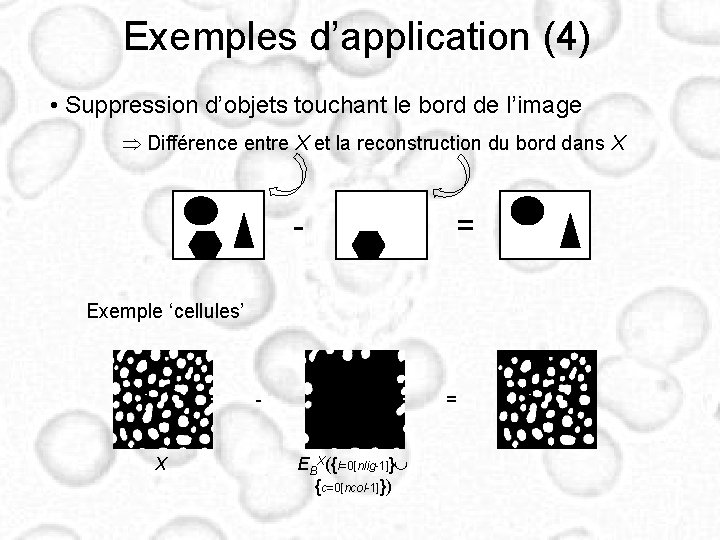
Exemples d’application (4) • Suppression d’objets touchant le bord de l’image Différence entre X et la reconstruction du bord dans X - = Exemple ‘cellules’ X = EBX({l=0[nlig-1]} {c=0[ncol-1]})

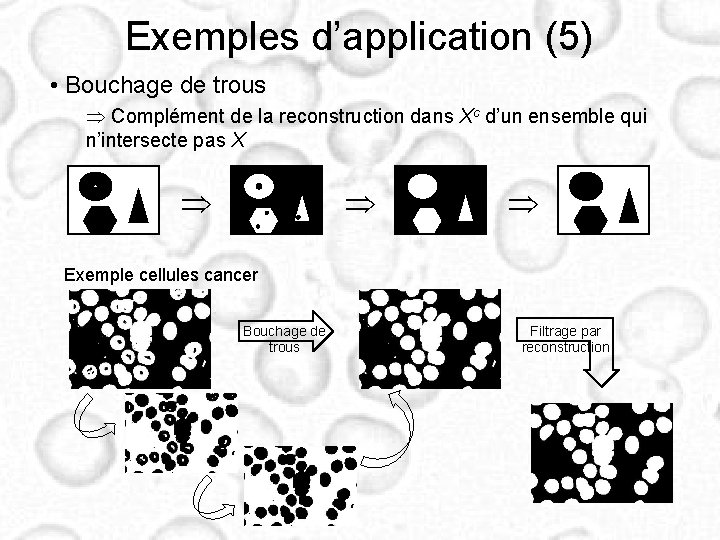
Exemples d’application (5) • Bouchage de trous Complément de la reconstruction dans Xc d’un ensemble qui n’intersecte pas X Exemple cellules cancer Bouchage de trous Filtrage par reconstruction

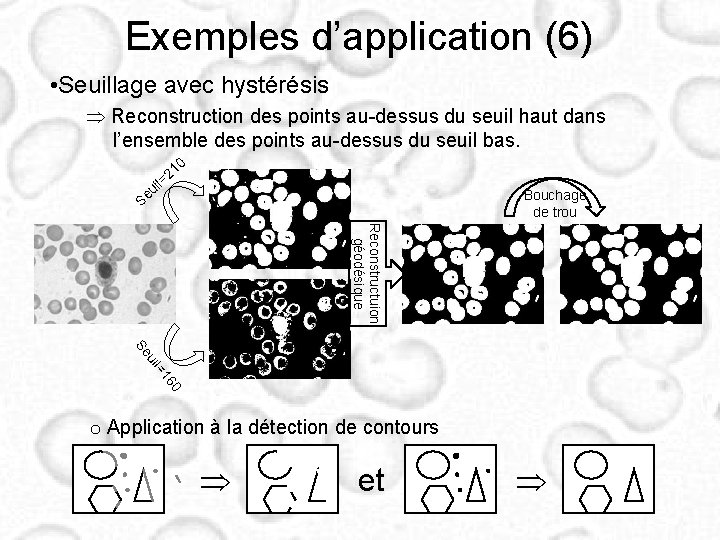
Exemples d’application (6) • Seuillage avec hystérésis Reconstruction des points au-dessus du seuil haut dans l’ensemble des points au-dessus du seuil bas. 0 ui e S 1 =2 l Bouchage de trou Reconstructuion géodésique 0 16 l= ui Se o Application à la détection de contours et

Erodé ultime : définition / algorithme • Cas général (binaire) Ensemble des composantes connexes de X disparaissant à l’itération suivante lors d’une séquence d’érosions par un élément structurant élémentaire B 1 Pour chaque pixel (non déjà dans érodé ultime) disparaissant à l’itération t, calculer la composante connexe à t-1 et tester si tous les pixels ont effectivement disparus à t. • Cas d’un élément structurant disque Ensemble des maxima régionaux de la fonction distance de X à son complémentaire Algorithme : 1. 2. 3. Calcul de l’image des distances Calculer l’ensemble des maxima locaux Pour chaque maximum local (xs xt, t Vs) non déjà traité : 1. 2. 3. Reconstitution géodésique de la composante connexe à xs conditionnellement à l’image des valeurs supérieures à xs CC(xs) Si xt CC(xs): xt>xs, alors marquer comme traités les maxima locaux qui appartiennent à CC(xs) Sinon, alors xs est un maximum régional et CC(xs) érodé ultime

Erodé ultime : exemple par B Distances 8 -connexité, respectivement masque (1, 0), (4, 3, 0) et (11, 7, 5, 0) Érosions successives Distance 4 -connexité

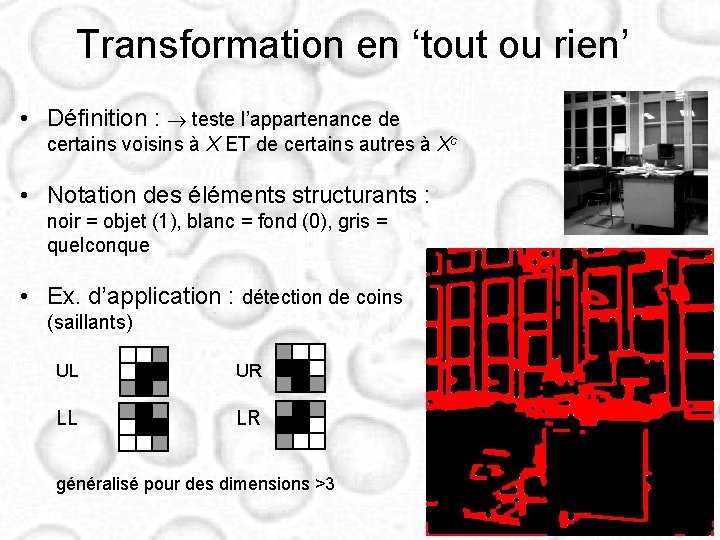
Transformation en ‘tout ou rien’ • Définition : teste l’appartenance de certains voisins à X ET de certains autres à Xc • Notation des éléments structurants : noir = objet (1), blanc = fond (0), gris = quelconque • Ex. d’application : détection de coins (saillants) UL UR LL LR généralisé pour des dimensions >3

Calcul de l’enveloppe convexe • Définition: L'enveloppe convexe d'un objet O est l’ensemble convexe (Ec / (A, B) 2 points de Ec, [A, B] est entièrement contenu dans Ec) le plus petit parmi ceux incluant O. • épaississement (ajout des points sélectionnés) par la transformation en Tout ou Rien suivante : 12 elts struct. • Exemple : avec 1 elt. struct. 3 3, il n’est pas possible de gérer des pentes autres que {0, /2, /4, 3 /4}

Squelette morphologique : définition • Exemples de propriétés souhaitées : Même forme, respect des parties allongées, etc… – Préservation de la géométrie, de la topologie – Invariance aux translations, rotations, homothéties – Réversibilité, continuité, épaisseur nulle La forme peut être retrouvée connaissant le squelette et la taille des érosions (p. e. ). Mêmes nombres de composantes connexes, de trous. 1 ‘petite’ variation de forme engendre 1 petite variation du squelette. • Squelette morphologique euclidien (cas continu) U des centres des boules maximales (contenues ds X) • Cas discret : U des résidus d’ouverture des érodés successifs : Épaisseur nulle, réversible Mais ne préserve pas la topologie, ex: non continu, ex:

Homotopie discrète et simplicité • Définition : F fct de R 2 préserve la topologie si A ouvert, A et F(A) sont homotopes • Cas discret : A’ K-homotope à A 2 bijections préservant la relation d’entourage (au sens du théorème de Jordan) entre : (i) les ensembles des K-cc (K {4, 8}) de A et de A’, (ii) les ensembles des K’-cc (K’=12 -K) de Ac et de (A’)c pour A’ A (i) toute K-cc (K {4, 8}) de A contient exactement 1 K-cc de A’ et (ii) toute K’-cc (K’=12 -K) de (A’)c contient exactement 1 K’-cc de Ac • Définition : x point K-simple dans X X-{x} homotope à X x a au moins 1 K’-voisin dans Xc et x est K-voisin d’ 1 seule K-cc de X se calcule en examinant les 8 voisins

Homotopie discrète et simplicité • Propriété : x est K-simple NKX(x)=1 • Retrait des points K-simples : x 3 x 2 x 1 x 4 x x 0, x 8 x 5 x 6 x 7 Une union de points K-simples n’est pas nécessairement 1 ens. simple, ex : y x et y sont simples mais pas {x, y} x – séquentiel perte des propriétés métriques, – parallèle risque de perte de l’homotopie – solution : ‘¼ parallèle’ : on ne retire ensemble que les points qui ont 1 voisin ‘Nord’ (resp. ‘Est’, ‘Sud’, ‘Ouest’) dans Xc • Rq : noyau homotopique ne préserve pas la forme de X utilisation de ‘points d’ancrage’

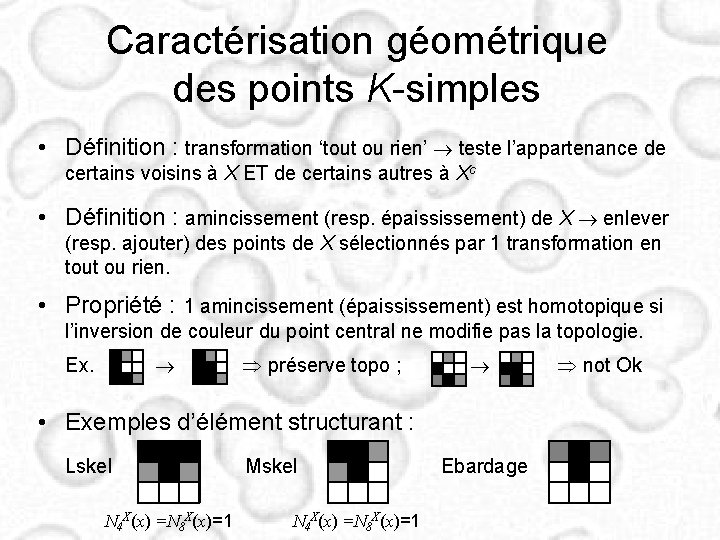
Caractérisation géométrique des points K-simples • Définition : transformation ‘tout ou rien’ teste l’appartenance de certains voisins à X ET de certains autres à Xc • Définition : amincissement (resp. épaississement) de X enlever (resp. ajouter) des points de X sélectionnés par 1 transformation en tout ou rien. • Propriété : 1 amincissement (épaississement) est homotopique si l’inversion de couleur du point central ne modifie pas la topologie. Ex. préserve topo ; • Exemples d’élément structurant : Lskel N 4 X(x) =N 8 X(x)=1 Mskel N 4 X(x) =N 8 X(x)=1 Ebardage not Ok

Squelette morphologique : algorithme • Rq : noyau homotopique ne préserve pas la forme de X utilisation de ‘points d’ancrage’ , e. g. maxima locaux de la distance • Algorithme préservant la topologie : – Initialiser S(X) à X – Répéter (jusqu’à avoir traité tous les points de X) : • Soit ESd les points de S(X) ayant un voisin immédiat dans (S(X))c dans la direction ‘Nord’ (resp. ‘Est’, ‘Sud’, ‘Ouest’) • Déterminer LK-s l’ensemble (parmi les points de ESd) des points ‘K-simples’ (en K connexité) • Retirer simultanément de S(X) tous les points de LK-s (sauf points d’ancrage) • Changer la direction considérée (N, E, S, ou O) • Informatiquement, utilisation de ‘piles’ de pixels

1 1 1 2 2 1 1 1 1 2 2 2 1 1 2 1 2 2 2 1

Exemple : X 8 -connexité 4 -connexité Itérations 0, 1, 2 Itérations 3, 4, 5 Itérations 6, 7, 8

Squelette par zones d’influence (SKIZ) • Définition : Soit X compact de R 2, la zone d’influence d’une composante connexe Xi de X est l’ens. des points plus près de Xi que de tout autre composante Le SKIZ est la frontière des zones d’influence • Calcul du SKIZ : 1. Amincissement du fond par Lskel 2. Puis ébardage du résultat de 1. • Ex :

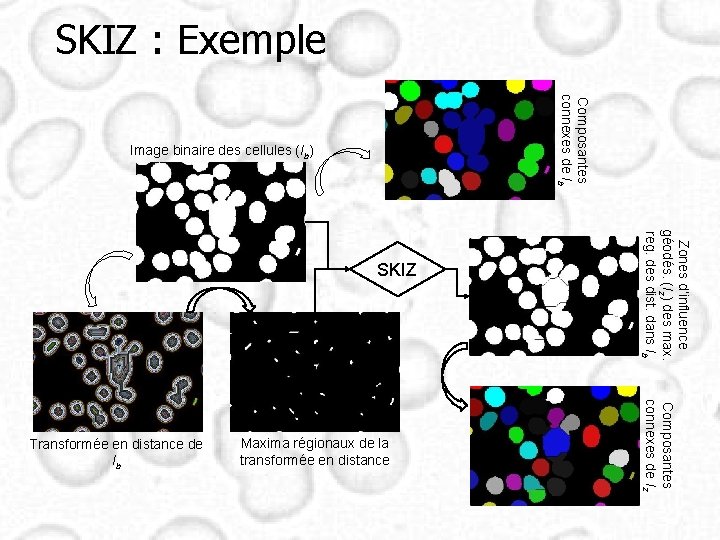
SKIZ : Exemple Composantes connexes de Ib Image binaire des cellules (Ib) Maxima régionaux de la transformée en distance Composantes connexes de Iz Transformée en distance de Ib Zones d’influence géodés. (Iz) des max. reg. des dist. dans Ib SKIZ

Exercice • Soit l’image suivante : On cherche à compter les différents types de cellules et leur proportions respectives. Proposez une solution, décrivez le synoptique de l’algorithme à mettre en œuvre et les fonctions à développer (notamment les entrées / sorties), puis pour chacune d’elles le pseudo-code.

Seuillage par valeurs inférieures Image niveaux de gris Élimination des objets touchant le bord Image binaire filtrée Image binaire Elagage Image des squelettes des particules Filtrage par érosionreconstruction Squelette Image des squelettes des particules Classification selon forme (ronde/allongée) Image binaire filtrée Etiquettage en composantes connexes Image des particules classées Image segmentée des particules Liste des objets avec étiquettes