Eclectism Shrinks Even Small Worlds Pierre Fraigniaud CNRS

Eclectism Shrinks Even Small Worlds Pierre Fraigniaud (CNRS, Univ. Paris Sud) joint work with Cyril Gavoille (Univ. Bordeaux) Christophe Paul (Univ. Montpellier)

Milgram’s Experiment • Source person s (e. g. , in Wichita) • Target person t (e. g. , in Cambridge) • Name, occupation, etc. • Letter transmitted via a chain of individuals related on a personal basis • Result: The “six degrees of separation”

Formal support to the 6 degrees Watts and Strogatz: augmented graphs H=(G, D) • Individuals as nodes of a graph G • Edges of G model relations between individuals deducible from their societal positions • D = probabilistic distribution • “Long links” = links added to G at random, according to D • Long links model relations between individuals that cannot be deduced from their societal positions

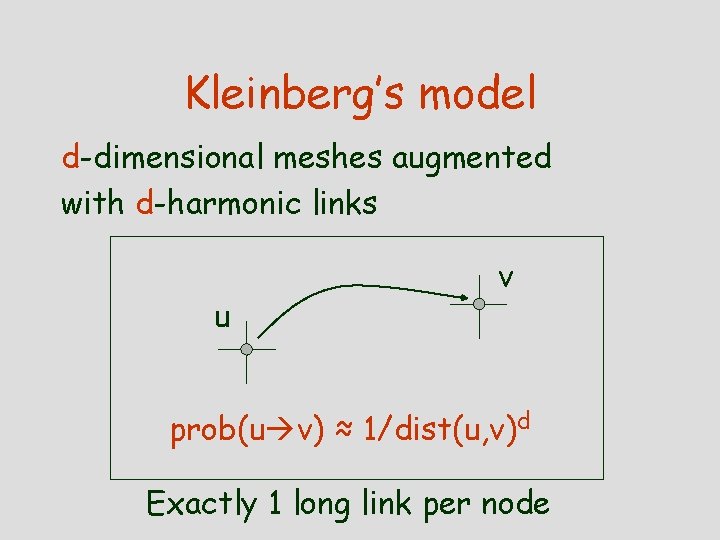
Kleinberg’s model d-dimensional meshes augmented with d-harmonic links u v prob(u v) ≈ 1/dist(u, v)d Exactly 1 long link per node

Greedy Routing • Source s = (s 1, s 2, …, sd) • Target t = (t 1, t 2, …, td) • Current node x selects, among its 2 d+1 neighbors, the closest to t in the mesh, y. Action: Node x sends to y.

Performances of Greedy Routing B=ball radius m/2 “jump” t “jump” x dist. G(x, t)=m O(log n) expect. #steps to enter B O(log 2 n) expect. #steps to reach t from s

Limit of Kleinberg’s model • d = #dimensions of the mesh ≈ #criterions for the search of t • Performances of greedy routing in d-dimensional meshes: O(log 2 n) expected #steps independent of #criterions

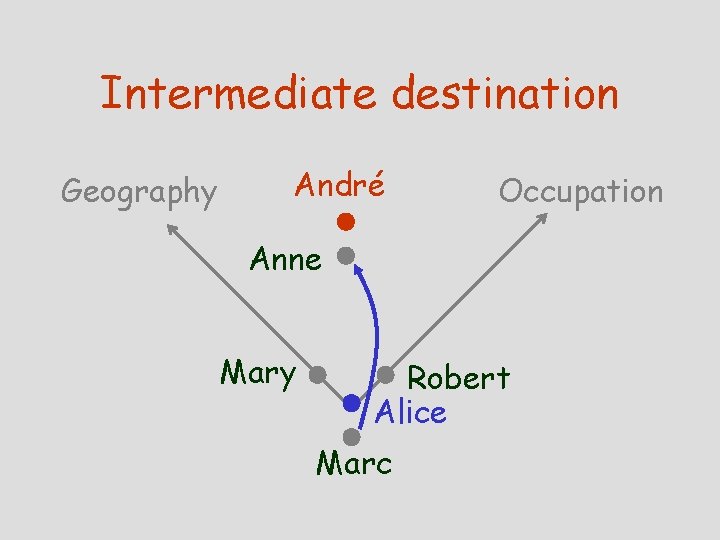
Intermediate destination Geography André Occupation Anne Mary Robert Alice Marc

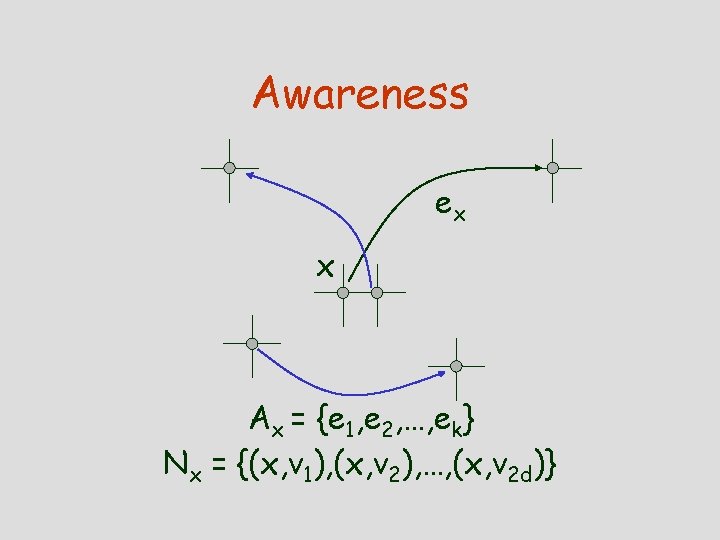
Awareness ex x Ax = {e 1, e 2, …, ek} Nx = {(x, v 1), (x, v 2), …, (x, v 2 d)}

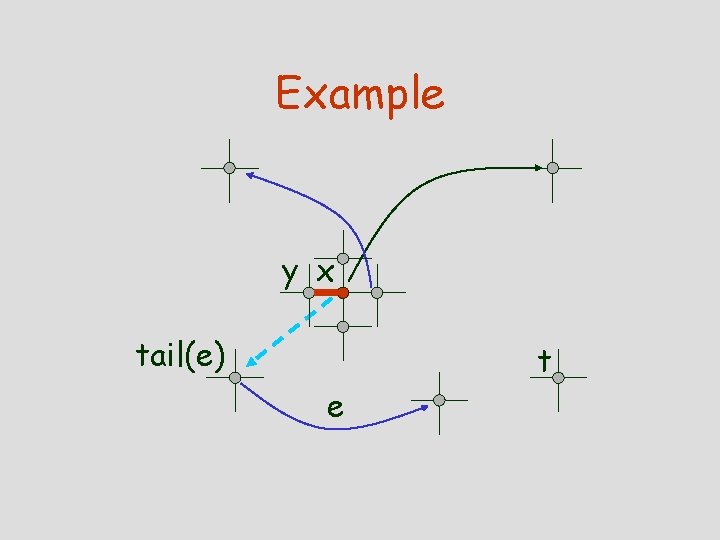
Indirect-Greedy Routing Two phases: Phase 1: Among all edges in Ax U Nx current node x picks e such that head(e) is closest to t in the mesh. Phase 2: Current node x selects, among its 2 d+1 neighbors, the closest to tail(e) in the mesh, y. Action: Node x sends to y.

Example y x tail(e) t e

Convergence of Indirect Greedy Routing Definition: A system of awareness {Au/u V} is monotone if for every u, for every e Au -{eu}, the first node v on the greedy path from u to tail(e) satisfies e Av. Theorem: IGR converges if and only if the system of awareness is monotone. Example: Au = long links of the k closest neighbors of u in the mesh

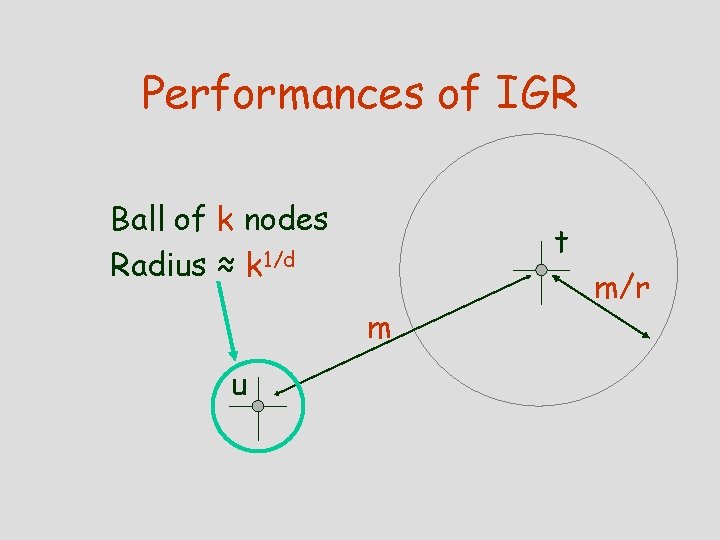
Performances of IGR Ball of k nodes Radius ≈ k 1/d t m u m/r

Tradeoff • Large awareness large expected #steps to reach ID small expected #phases “m m/r” • Small awareness small expected #steps to reach ID large expected #ID before “m m/2”

Case |Au|=O(log n) • Theorem: If every node is aware of the long links of its O(log n) closest neighbhors, then IGR performs in O(log 1+1/dn) expected #steps. • Proof: O(log 1/dn) exp. #steps to reach ID O(log n) exp. #steps m m/2

Consequences • GR does not take #criterions into account O(log 2 n) exp. #steps • IGR takes #criterions into account O(log 1+1/dn) exp. #steps Eclecticism shrinks even small worlds

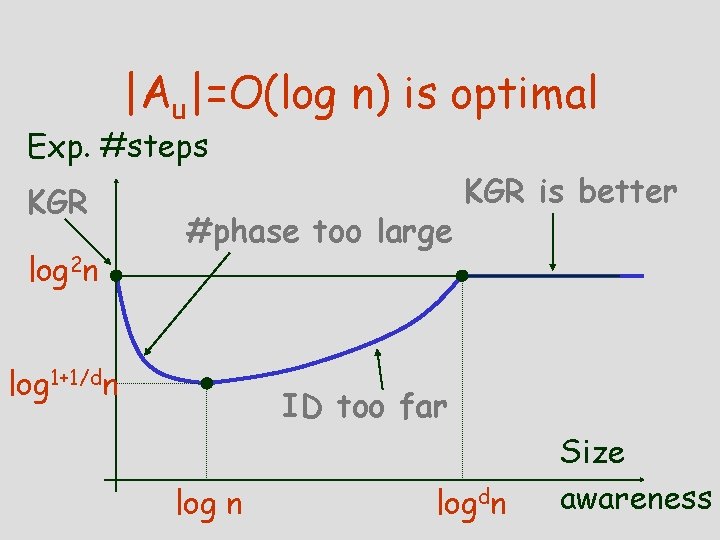
|Au|=O(log n) is optimal Exp. #steps KGR log 2 n #phase too large log 1+1/dn KGR is better ID too far log n logdn Size awareness

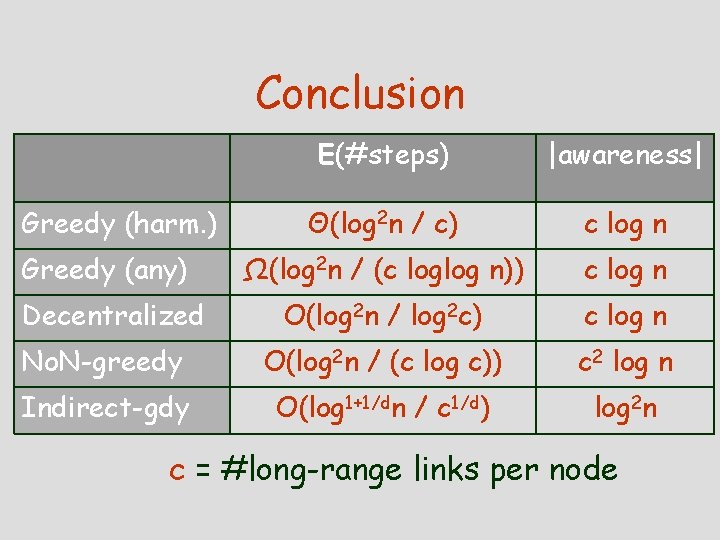
Conclusion E(#steps) |awareness| Θ(log 2 n / c) c log n Greedy (any) Ω(log 2 n / (c loglog n)) c log n Decentralized O(log 2 n / log 2 c) c log n No. N-greedy O(log 2 n / (c log c)) c 2 log n Indirect-gdy O(log 1+1/dn / c 1/d) log 2 n Greedy (harm. ) c = #long-range links per node