SLn R and Diffn R Decontraction formula and






































- Slides: 39

SL(n, R) and Diff(n, R) Decontraction formula and Unitary Irreducible Representations Djordje Sijacki and Igor Salom Institute of Physics, University of Belgrade Quantum Integrable Systems and Geometry, September 2012, Olhao, Portugal

sl(n, R) and diff(n, R) algebras in gravity and HEP • Affine models of gravity in n space-time dimensions (gauging Rn Λ GL(n, R) symmetry) • “World spinors” - infinite-component Diff(n, R) spinors in n space-time dimensions • Systems with conserved n-dimensional volume (strings, p. D-branes. . . ) • SL(3, R), SL(4, R) unirreps and Regge trajectories of hadrons (3 -quark and quark-antiquark bound states) • Chromogravity as an effective IR region QCD

Cromogravity – Effective QCD in the IR region SU(3) color gauge – B is dressed gluon field, g is SU(3) Cartan metric SU(3) variation: Expand B around a constant vacuum solution N (pure gauge) of the instanton type:

In the IR region (variation of pseudo-metric G):

Generalization to colorless n-gluon fields: d is the color SU(3) totally symmetric 8 x 8 x 8 → 1 tensor QCD variation in the IR region:

Operators of the Chromo-Diffeomorphism algebra

- Diff(n, R) linearly realized - Diff(n, R) realized nonlineary over SL(n, R)

Spinorial matter fields of SL(n, R), GL(n, R) and/or Diff(n, R) nonlinearly realized w. r. t. SL(n, R), are infinite-component fields coupled to GL(n, R) connections: Q are the SL(n, R), GL(n, R) group generators (infinite matrices!) Frame fields: Infinite pseudo-frame (alephzeroads)

Affine theory of gravity • A generic affine theory Lagrangian in n space-time dimensions : • A symmetry breaking mechanism is required.

DOUBLE COVERING of SL(n, R), GL(n, R) and Diff(n, R) Iwasawa decomposition of a semisimple Lie algebra: g=k+a+n; G=Kx. Ax. N is any connected group with Lie algebra g, K (compact), A (Abelian) and N (nilpotent) are its corresponding analytic subgroups – the groups A and N are simply connected. There exists a universal covering group where Is the universal covering of K. For SL(n, R), GL(n, R), the universal covering group of K=SO(n) is a double covering given by Spin(n)

For the group of diffeomorphisms Stewart proved: Diff(n, R) where the subgroup H is contractible to a point. As a result, as O(n) is the compact subgroup of GL(n, R), there is a double cover: For SL(4, R)

A finite dimensional covering of SL(n, R), i. e. Diff(n, R) exists provided one can embed their covering into a group of finite complex matrices that contain Spin(n) as a subgroup. The natural candidate for SL(n, R) covering, from the set of Cartan's classical Lie groups, is SL(n, C), however there is no match of the group dimensionalities, i. e. dim(SL(n, C)) = n < dim(Spin(n)) = 2^[(n-1)/2] except for n=8, but than the maximal compact subgroup of SL(8, C) is SO(8) and not Spin(8)! The universal (double) coverings of SL(n, R), GL(n, R) and Diff(n, R), for n>2, are groups of infinite complex matrices.

SL(n, R) generetors representations I is necessary to know, for various (math) physics applications, how to represent the SL(n, R) generators, i. e. to find their infinitedimensional unirreps. . . … in some simple, “easy to use” form, … in SO(n) (or SO(1, n-1)) subgroup basis, … for infinite-dimensional unitary representations, … and, in particular, for infinite-dimensional spinorial representations!

How to find SL(n, R) generators? • • • Induction from parabolic subgroups Construct generators as differential operators in the space of group parameters Analytical continuation of complexified SU(n) representations. . . By making use of the Gell-Mann decontraction formula

Now, what is the Gell-Mann decontraction formula? Loosely speaking: it is formula inverse to the Inönü-Wigner contraction.

The Gell-Mann decontraction formula Inönü-Wigner contraction Gell-Mann ? formula Gell-Mann formula (as named by R. Hermann)

Example: Poincare to de Sitter • Define function of Poincare generators: • Check: • …unfortunately, this works so nicely only for so(m, n) cases. Not for sl(n, R).

SL(n, R) group • Definition: group of unimodular n x n real matrices (with matrix multiplication) • Algebra relations: so(n) irrep. of traceless symmetric matrices

Inönü-Wigner contraction of SL(n, R) Find representations of the contracted semidirect product and apply Gell-Mann formula to get sl(n, R) representations. SL(n, R) Rn(n+1)/2 -1 Λ Spin(n) Representations of this group are rather easy to find

Space of square integrable functions over Spin(n) manifold • Space of square integrable functions is rich enough to contain representatives from all equivalence classes of irreps. of both SL(n, R) and Tn(n+1)/2 -1 Λ Spin(n) groups (Harish Chandra). • As a basis we choose Wigner D functions: k indices label SL(n, R) SО(n) multiplicity Chain of groups: Spin(n); Spin(n-1), Spin(n-2), …, Spin(2)

Contracted algebra representations • Contracted abelian operators U represent as multiplicative Wigner D functions: • Action of spin(n) subalgebra is “natural” one: Matrix elements are simply products of Spin(n) CG coefficients

Try to use Gell-Mann formula • Take and plug it in the Gell-Mann formula, i. e. : and then check commutation relations. • works only in spaces over SO(n)/(SO(p)×SO(q)), q+p=n • no spinorial representations here • no representations with multiplicity w. r. t. Spin(n) → Insufficient for most of physical applications! (“Conditions for Validity of the Gell-Mann Formula in the Case of sl(n, R) and/or su(n) Algebras”, Igor Salom and Djordje Šijački, in Lie theory and its applications in physics, American Institute of Physics Conference Proceedings, 1243 (2010) 191 -198. )

Learning from the solved cases • All irreducible representations of SL(3, R) and SL(4, R) are known (Dj. Šijački, using different approach) • Matrix elements of SL(3, R) representations with multiplicity indicate an expression of the form: ! • This is a correct, “generalized” formula! Additional label, • Similarly in SL(4, R) case. overall 2, matching the group rank!

Spin(n) left action generators

Generalized formula in SL(5, R) case 4 labels, matching the group rank. new terms Not easy even to check that this is correct (i. e. closes algebra relations). Generalization of the Gell-Mann formula for sl(5, R) and su(5) algebras, Igor Salom and Djordje Šijački, International Journal of Geometric Methods in Modern Physics, 7 (2010) 455 -470.

Can we find the generalized formula for arbitrary n? • Idea: rewrite all generalized formulas (n=3, 4, 5) in Cartesian coordinates. • All formulas fit into a general expression, now valid for arbitratry n: • Using a D-functions identity: Overall n-1 parameters, matching the group rank! They Casimir direct calculation shows that the expression satisfiesdetermine algebra relations. values. Igor Salom and Djordje Šijački, International Journal of Geometric Methods in Modern Physics, 8 (2011), 395 -410

Matrix elements for arbitrary SL(n, R) irreducible representation • Matrix elements: • All required properties met: Simple closed expression in Spin(n) basis valid for arbitrary representation (including infinite dimensional ones, and spinorial ones, and with nontrivial multiplicity)!

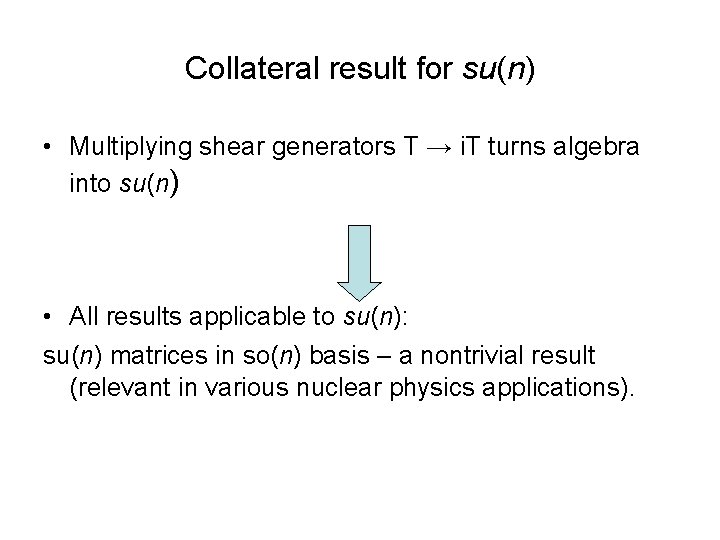
Collateral result for su(n) • Multiplying shear generators T → i. T turns algebra into su(n) • All results applicable to su(n): su(n) matrices in so(n) basis – a nontrivial result (relevant in various nuclear physics applications).

UNITARY IRREDUCIBLE REPRESENTATIONS Harish-Chandra proved that all unitary irreducible representations of a noncompact group G can be obtained in Hilbert spaces H of square-integrable functions over the maximal compact subgroup K. Unitarity means that: and the additional conditions that the bilinear form is a scalar product are hermiticity and positive definiteness:

In order to obtain ALL unitary irreducible representations we consider the most general scalar product of functions over K=Spin(n), with an invariant measure dk and an arbitrary kernel function over Kx. K

Now we combine: (1) SL(n, R) generators matrix elements expressions for an arbitrary representation, as given by the generalized decontraction formula, (2) representation unitarity requirement, (3) scalar product hermiticity and positive definiteness, (4) irreducibility requirement, as given by invariant lattices of the Spin(n) labels weight space.

Simplest case: Principal series of (infite-dimensional) unitary irreducible (spinorial and tensorial) representations of the SL(n, R) double covering group: representation labels – purely imaginary kernel function – Dirac's delta function All matrix elements of the noncompact generators for an arbitrary unirrep given by generalized decontraction formula


Application – affine theory of gravity • A generic affine theory Lagrangian in n space-time dimensions : What kind of fields are these? • A symmetry breaking mechanism is required.

sl(n, R) matrix elements appear in vertices

Example: n=5, multiplicity free • Vector component of infinite-component bosonic multifield, transforming as a multiplicity free SL(5, R) representation labelled by • Similarly for the term:

Example: n=5, nontrivial multiplicity From the form of the generalized Gell-Mann formula we deduce that all component can not belong • Duetotothe multiplicity, there are , a priori, 5 different 5 -dimensional vector same irreducible components, i. e. Lorentz subfields, of the infinite-component bosonic representation multifield – one vector field for each valid combination of left indices k.

Example: n=5, nontrivial multiplicity • Sheer connection transforms these fields one into another. Interaction terms are:

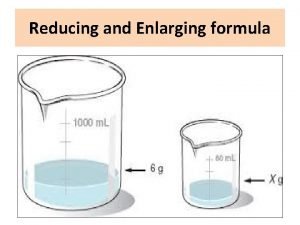
 Minizinc diffn
Minizinc diffn Sln mamma
Sln mamma Lesy mesta brezno
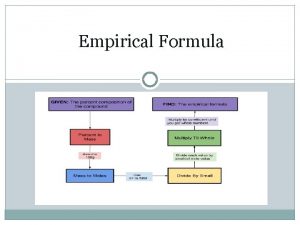
Lesy mesta brezno Which formula is an empirical formula?
Which formula is an empirical formula? Empirical formula of ibuprofen
Empirical formula of ibuprofen Empirical formula
Empirical formula Chapter 7 review chemical formulas and chemical compounds
Chapter 7 review chemical formulas and chemical compounds Define molecular formula
Define molecular formula Molecular formula
Molecular formula Recursive and explicit formulas
Recursive and explicit formulas Simple annual interest rate formula
Simple annual interest rate formula Trisilicon octaiodide chemical formula
Trisilicon octaiodide chemical formula Empirical formula of haemoglobin
Empirical formula of haemoglobin Nylon 6 empirical formula
Nylon 6 empirical formula Empirical formula of glucose
Empirical formula of glucose Change in heat formula
Change in heat formula Geometric sequences and exponential functions
Geometric sequences and exponential functions Difference between molecular and covalent
Difference between molecular and covalent Explicit vs recursive
Explicit vs recursive Explicit and recursive formulas
Explicit and recursive formulas Explicit versus recursive
Explicit versus recursive Arithmetic vs geometric
Arithmetic vs geometric Recursive formulas
Recursive formulas How to find the empirical formula from percent composition
How to find the empirical formula from percent composition Molecular formular
Molecular formular Formula of butanoic acid
Formula of butanoic acid Formula mass vs gram formula mass
Formula mass vs gram formula mass Formula mass vs gram formula mass
Formula mass vs gram formula mass Li+ and po43- formula
Li+ and po43- formula Human resource cost accounting
Human resource cost accounting Variance formula in standard deviation
Variance formula in standard deviation Permutation and combination formula
Permutation and combination formula Two nonadjacent angles formed by two intersecting lines
Two nonadjacent angles formed by two intersecting lines Naming and writing formulas
Naming and writing formulas Geometric sequence formula
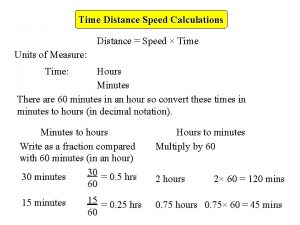
Geometric sequence formula Calculating time with distance and speed
Calculating time with distance and speed Pdf of poisson distribution formula
Pdf of poisson distribution formula Relationship between pressure, volume and temperature
Relationship between pressure, volume and temperature Lesson 5-1 distance and midpoint formulas
Lesson 5-1 distance and midpoint formulas Distance spped time
Distance spped time