ARITHMETIC SEQUENCES EXPLICIT AND RECURSIVE FORMULAS UNIT 1

ARITHMETIC SEQUENCES & EXPLICIT AND RECURSIVE FORMULAS UNIT 1

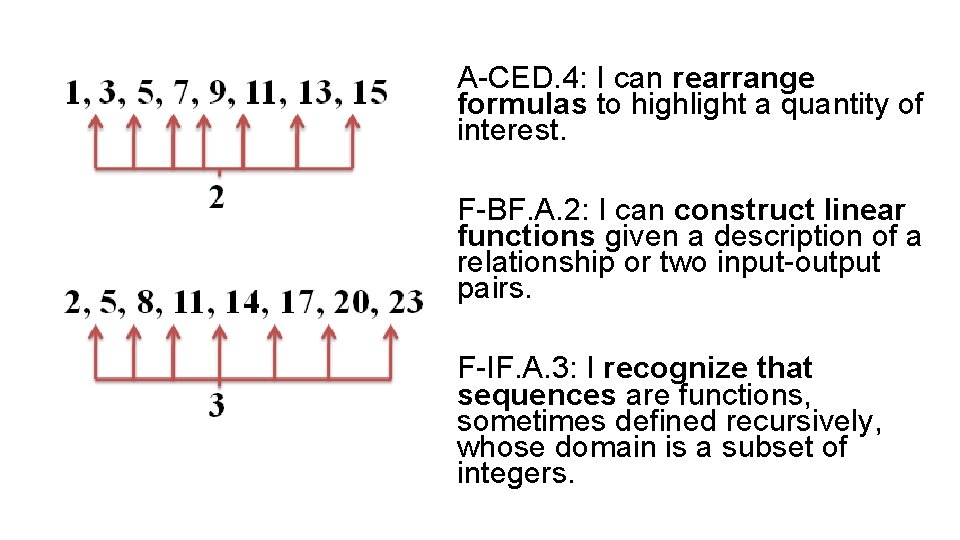
A-CED. 4: I can rearrange formulas to highlight a quantity of interest. F-BF. A. 2: I can construct linear functions given a description of a relationship or two input-output pairs. F-IF. A. 3: I recognize that sequences are functions, sometimes defined recursively, whose domain is a subset of integers.

EXPLORATION You have been offered a job paying $28, 000 in the first year. You anticipate receiving a $1500 raise each year for the next 7 years. How much will you be earning in the 8 th year? How much will you earn over the 8 -year period?

How much will you be earning in the 8 th year? $28000 +$1500+$1500+$1500+$1500 = $38, 500 How much will you earn over the 8 -year period? $28000+$29500+$31000+$32500+$34000+$35500+$37000+$38500 = $266, 000

HOW TO DEFINE AN EXPLICIT AND RECURSIVE FORMULA FOR AN ARITHMETIC SEQUENCE Take notes while watching the video. Only watch a portion of this video (0: 00 – 4: 20) https: //www. khanacademy. org/math/precalculus/seq-induction/sequencesreview/v/arithmetic-sequences

IDENTIFYING ARITHMETIC SEQUENCES Decide whether each sequence is arithmetic.

IDENTIFYING ARITHMETIC SEQUENCES Decide whether each sequence is arithmetic.

IDENTIFYING ARITHMETIC SEQUENCES Decide whether each sequence is arithmetic.

IDENTIFYING ARITHMETIC SEQUENCES Decide whether each sequence is arithmetic.

GUIDED PRACTICE EXAMPLE 1

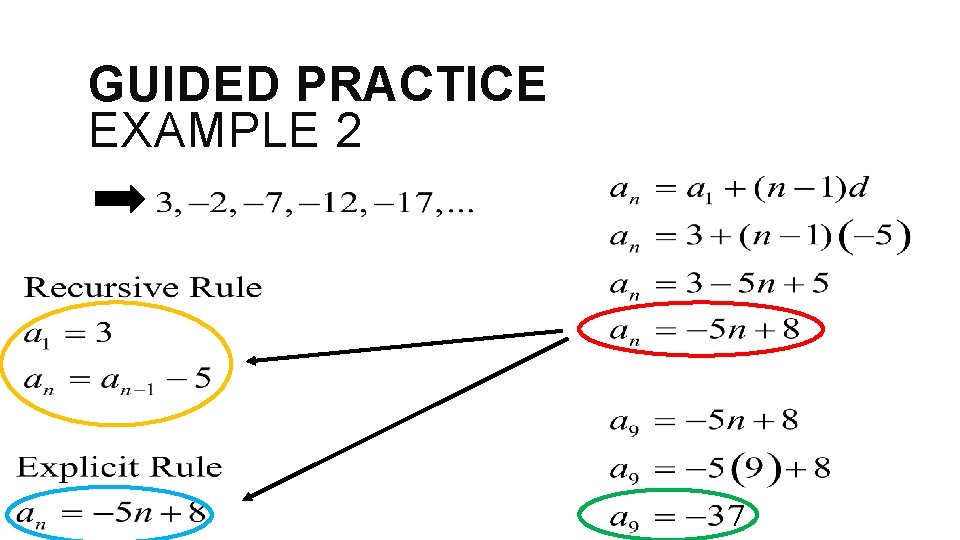
GUIDED PRACTICE EXAMPLE 2

GUIDED PRACTICE EXAMPLE 2

INDEPENDENT PRACTICE EXAMPLE 3 Determine if each pattern is an arithmetic sequence. If so, rewrite the sequence as an explicit and recursive rule. Evaluate the sequence for the given nth term.

INDEPENDENT PRACTICE EXAMPLE 3

INDEPENDENT PRACTICE EXAMPLE 3

INDEPENDENT PRACTICE EXAMPLE 3

INDEPENDENT PRACTICE EXAMPLE 3

INDEPENDENT PRACTICE EXAMPLE 3

INDEPENDENT PRACTICE EXAMPLE 3

INDEPENDENT PRACTICE EXAMPLE 3

INDEPENDENT PRACTICE EXAMPLE 3

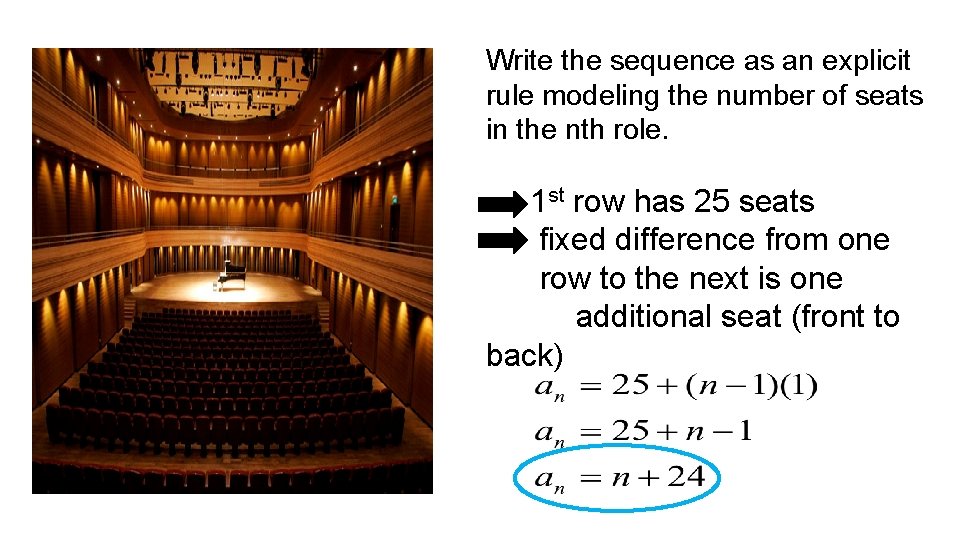
The first row of a concert hall has 25 seats, and each row after the first has one more seat than the row before it. There are 32 rows of seats. Write the sequence as an explicit rule modeling the number of seats in the nth role. Thirty-five students from a class want to sit in the same row. How close to the front can they sit?

Write the sequence as an explicit rule modeling the number of seats in the nth role. 1 st row has 25 seats fixed difference from one row to the next is one additional seat (front to back)

Thirty-five students from a class want to sit in the same row. How close to the front can they sit? The class can sit in the 11 th row.

Suppose you buy a $500 camcorder on layaway by making a down payment of $150 and then paying $25 per month. Write a recursive rule for the total amount of money paid on the camcorder at the beginning of the nth month. How much will you have left to pay on the camcorder at the beginning of the twelfth month?

Write a recursive rule for the total amount of money paid on the camcorder at the beginning of the nth month.

How much will you have left to pay on the camcorder at the beginning of the twelfth month? At the beginning of the twelfth month, you would still own