DISTANCE FORMULA MIDPOINT FORMULA CIRCLES DISTANCE FORMULA Q

DISTANCE FORMULA, MIDPOINT FORMULA, CIRCLES

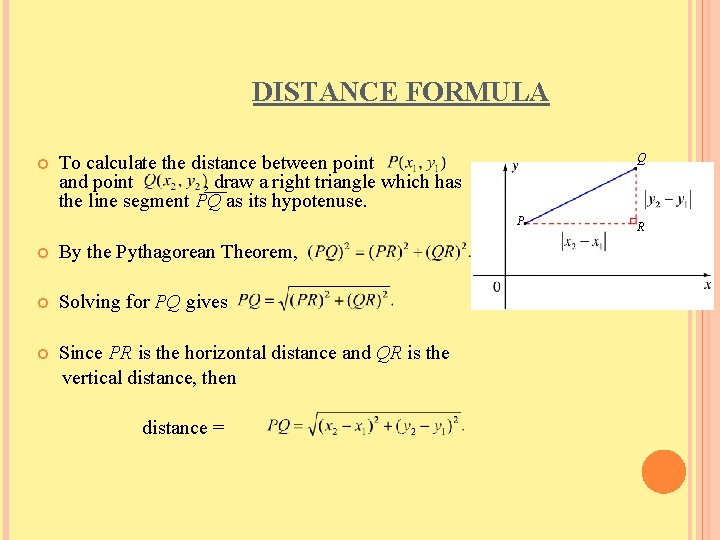
DISTANCE FORMULA Q To calculate the distance between point and point , draw a right triangle which has the line segment PQ as its hypotenuse. P By the Pythagorean Theorem, Solving for PQ gives Since PR is the horizontal distance and QR is the vertical distance, then distance = R

§ Problem: Find the distance between the following pairs of points. a) (– 3, 4) and (1, 7) b) (5, – 7) and (11, – 2) § Solution: a) b)

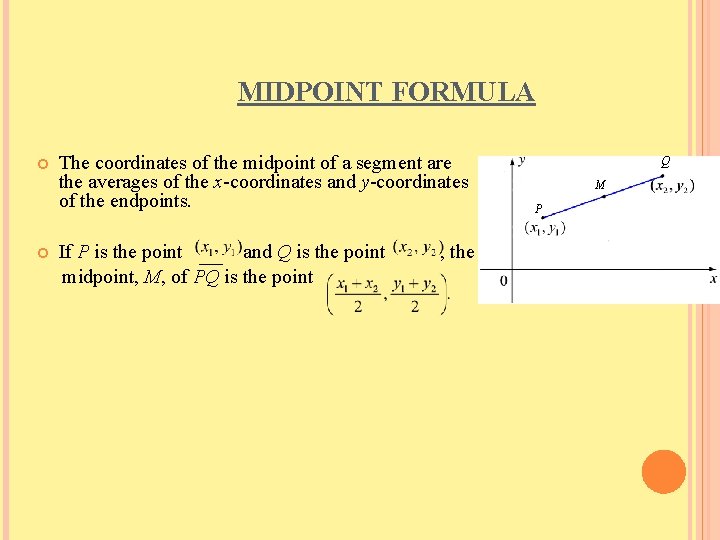
MIDPOINT FORMULA The coordinates of the midpoint of a segment are the averages of the x-coordinates and y-coordinates of the endpoints. If P is the point and Q is the point midpoint, M, of PQ is the point , the Q M P

§ Problem: Find the midpoint of each line segment with the given endpoints. a) (– 1, 3) and (5, – 9) b) (5, – 8) and (2, 0) § Solution: a) b)

EQUATION OF A CIRCLE The equation of a circle can be determined using the distance formula. Let C = (h, k) be the center of the circle. Let r be the radius. Let P = (x, y) be a point on the circle. Since PC = r, then (PC) = r. So squaring the distance from P to C would square the radius. Therefore, is the equation of the circle in standard form.

§ Problem: Identify the center and radius of each circle whose equation is given. a) b) § Solution: a) Center (1, 4), r = 3 b) Center (7, – 5), r = 10

§ Problem: Write the equation of a circle with the given center and radius. a) Center (– 3, 8), r = 4 b) Center (– 1, – 9), r = 7 § Solution: a) b)

SOMETIMES THE EQUATION OF THE CIRCLE MUST BE PUT BACK INTO STANDARD FORM SO THAT THE CENTER AND RADIUS CAN BE SEEN: First, move over the constant and swap the x term and the y squared terms: Second, complete the square with the x term and the y term: half the coefficient of each square -4/2 = -2 -2 X -2 = 4 add to both sides Factor the x’s and the y’s: Now the center is (2, -5) and the radius is 6. 10/2 = 5 5 X 5 = 25