Similar Triangles Geometry ANGLEANGLE SIMILARITY POSTULATE AA If










- Slides: 19

Similar Triangles Geometry

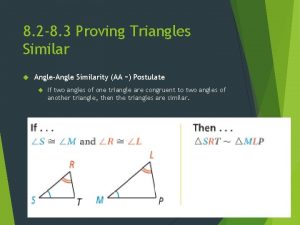
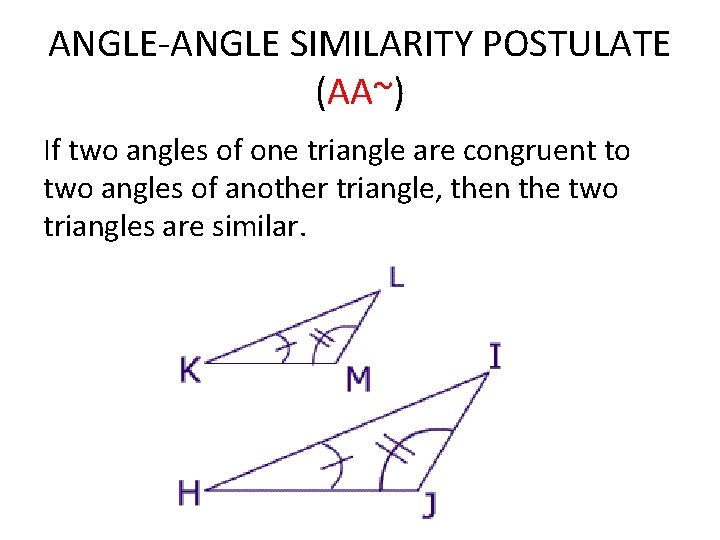
ANGLE-ANGLE SIMILARITY POSTULATE (AA~) If two angles of one triangle are congruent to two angles of another triangle, then the two triangles are similar.

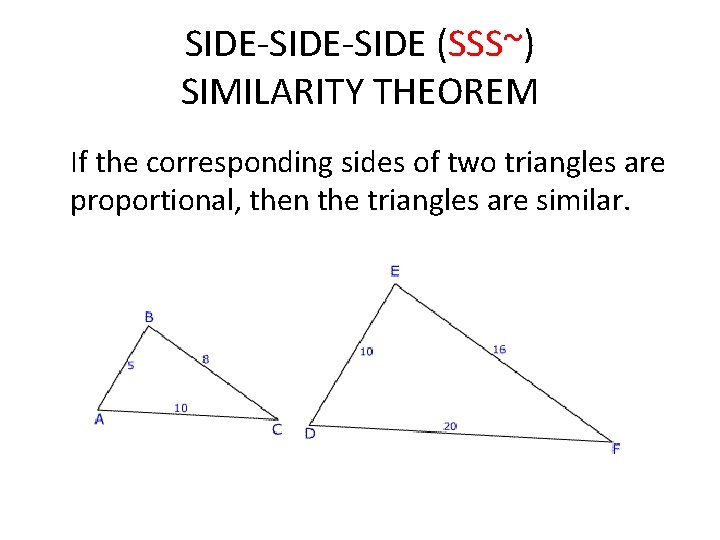
SIDE-SIDE (SSS~) SIMILARITY THEOREM If the corresponding sides of two triangles are proportional, then the triangles are similar.

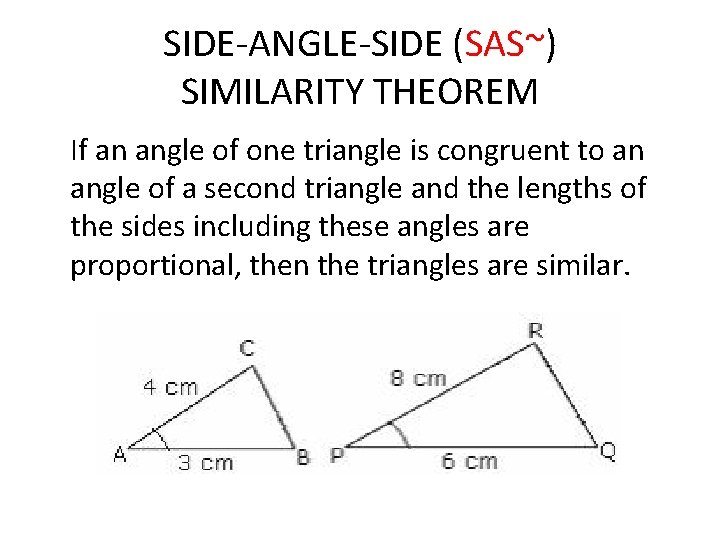
SIDE-ANGLE-SIDE (SAS~) SIMILARITY THEOREM If an angle of one triangle is congruent to an angle of a second triangle and the lengths of the sides including these angles are proportional, then the triangles are similar.

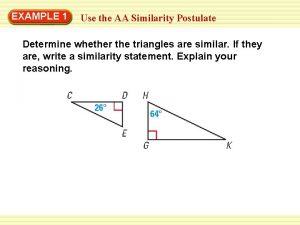
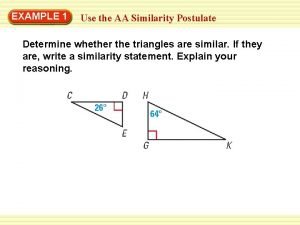
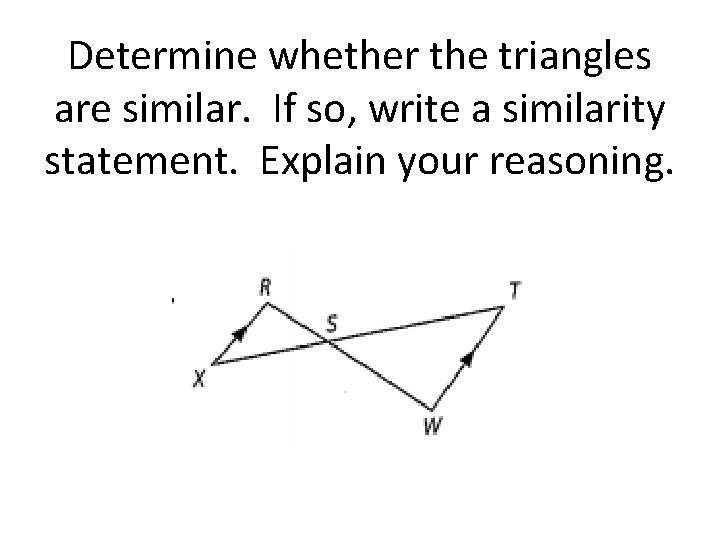
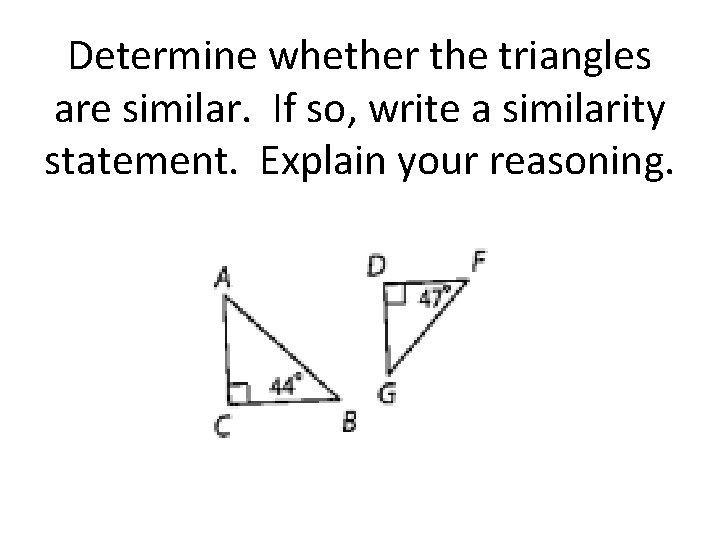
Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

Example In the figure, ∠ADB is a right angle. Which of the following would not be sufficient to prove that ∆ADB ~ ∆CDB?

Properties of Similarity is Reflexive, Symmetric, and Transitive!

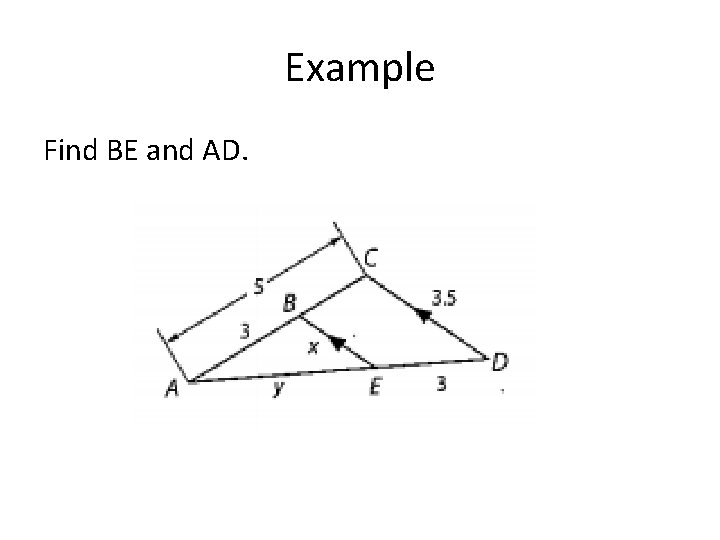
Example Find BE and AD.

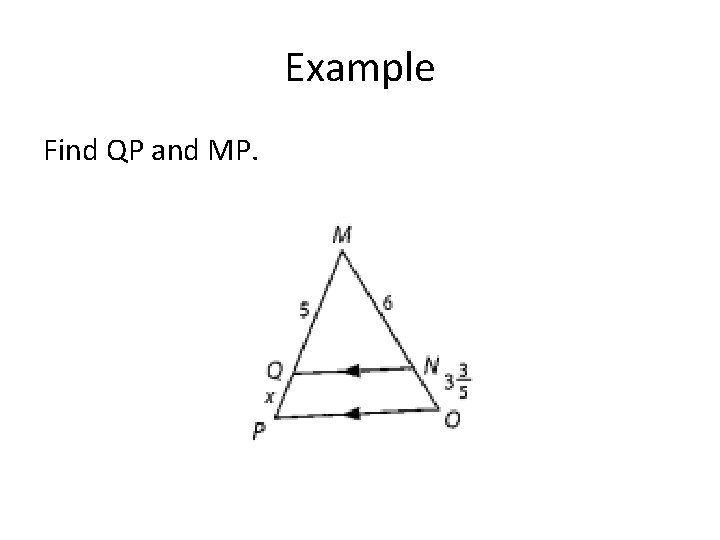
Example Find QP and MP.

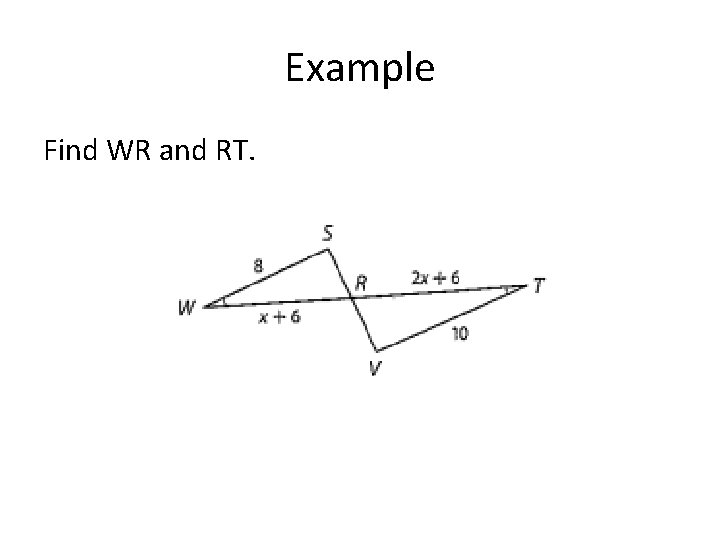
Example Find WR and RT.


Example You are at an indoor climbing wall. To estimate the height of the wall, you place a mirror on the floor 85 feet from the base of the wall centered in the mirror. You are 6. 5 feet from the mirror and your eyes are 5 feet above the ground. Use similar triangles to estimate the height of the wall.

Example Hallie is estimating the height of the Superman roller coaster in Mitchellville, Maryland. She is 5 feet 3 inches tall and her shadow is 3 feet long. If the length of the shadow of the roller coaster is 40 feet, how tall is the roller coaster?

Example At another indoor climbing wall, a person whose eyes are 6 feet from the floor places a mirror on the floor 60 feet from the base of the wall. They then walk backwards 5 feet before seeing the top of the wall in the center of the mirror. Use similar triangles to estimate the height of this wall.

Example Adam is standing next to the Palmetto Building in Columbia, South Carolina. He is 6 feet tall and the length of his shadow is 9 feet. If the length of the shadow of the building is 322. 5 feet, how tall is the building?
 Unit 3 similarity lesson 3 proving triangles similar
Unit 3 similarity lesson 3 proving triangles similar 7-3 assignment similar triangles
7-3 assignment similar triangles Similar
Similar Sss sas asa aas
Sss sas asa aas Aa similarity theorem
Aa similarity theorem Aa similarity theorem
Aa similarity theorem Aa similarity examples
Aa similarity examples Aa postulate
Aa postulate Segment addition postulate proof
Segment addition postulate proof Geometry basics segment addition postulate
Geometry basics segment addition postulate Geometry chapter 7 proportions and similarity answers
Geometry chapter 7 proportions and similarity answers Similarity ratio
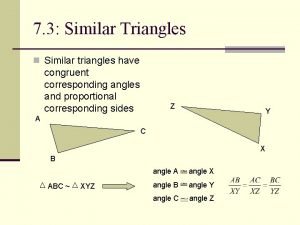
Similarity ratio Write a similarity statement comparing the two triangles.
Write a similarity statement comparing the two triangles. 9-4 similarity in right triangles
9-4 similarity in right triangles Similar right triangle
Similar right triangle Right triangle similarity theorem
Right triangle similarity theorem Lesson 8-1 similarity in right triangles
Lesson 8-1 similarity in right triangles Similarity in right triangles notes
Similarity in right triangles notes 7-4 lesson quiz similarity in right triangles
7-4 lesson quiz similarity in right triangles 7-3 similar triangles
7-3 similar triangles