Similar Experiences Similar Game Plans Similar Characters Similarity

Similar Experiences Similar Game Plans Similar Characters

Similarity in Geometric Figures Similarity in Geometry: - The concept that shapes or other relations exist in specific ratios or proportions to one another. Ratios: When two quantities are measured in the same units, (or can be converted to the same unit of measure), they can be expressed in a constant relation to one another, referred to as a ratio. Ratios are written: a / b or a: b Simplifying Ratios: Many times, the unit of measure provided will not always be the same. In those cases they need to be converted in order to specify a meaningful ratio. 12 cm 12 cm 4 m = 4* 100 cm 12 400 3 100 6 ft 18 in. 6 * 12 in. = 18 in. How might we convert these to simplified / meaningful ratios? 72 18 4 1

Using Ratios To Solve Problems D C The perimeter of a rectangle ABCD is 60 centimeters. The ratio of AB: BC is 3: 2. Find the length and width of the rectangle. Hint: Because the ratio o AB: BC is 3: 2, we can represent the length of AB as 3 x and BC as 2 x w A 2 l + 2 w = P 2(3 x) + 2(2 x) = 60 6 x + 4 x = 60 10 x = 60 X=6 Therefore, ABCD has a length of 18 cm and a width of 12 cm B l

Using Ratios To Solve Problems Extended Ratios: Ratios can extend beyond a simple relationship of two measures to incorporate a third, or more, provided they are all in a constant relation to one another. In the triangle ABC, the angles exist in the following extended ratio, 1: 2: 3. How can we use the extended ratio to determine the measure of the angles? x + 2 x + 3 x = 180 o 6 x = 180 X = 30 Triangle Sum Theorem Therefore the angle measures are 30 o, 60 o, and 90 o 2 x 3 x x

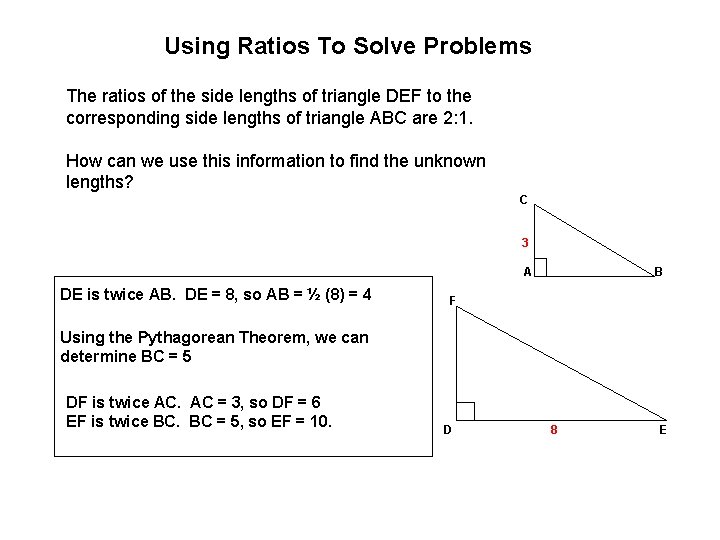
Using Ratios To Solve Problems The ratios of the side lengths of triangle DEF to the corresponding side lengths of triangle ABC are 2: 1. How can we use this information to find the unknown lengths? C 3 A DE is twice AB. DE = 8, so AB = ½ (8) = 4 B F Using the Pythagorean Theorem, we can determine BC = 5 DF is twice AC. AC = 3, so DF = 6 EF is twice BC. BC = 5, so EF = 10. D 8 E

Using Proportions An equation that equates two ratios is a proportion. For example, if the ratio a/b is equal to c/d, then the following proportion can be written: a/b = c/d The numbers “a” and “d” are referred to as the extremes. The numbers “b” and “c” are referred to as the means. Means Extremes a b c = d Properties of Proportions: 1. Cross Product Property – The product of the extremes equals the product of the means. If a/b = c/d, then ad = bc 2. Reciprocal Property – If two ratios are equal, then their reciprocals are also equal. If a/b = c/d, then b/a = d/c

Solving Proportions Using the Properties of Proportions, solve the following: 4/x=5/7 1. Using Cross Products: 5 x = 28 X = 28/5 2. Using Reciprocal Property 4/x = 5/7 x/4 = 7/5 x = 4(7/5) x = 28/5 3 =2 y+2 y 1. Using Cross Products 3 y = 2(y + 2) 3 y = 2 y + 4 y=4

What do these all have in common?

Additional Properties of Geometry in Proportions Properties of Proportions: 1. Cross Product Property – The product of the extremes equals the product of the means. If a/b = c/d, then ad = bc 2. Reciprocal Property – If two ratios are equal, then their reciprocals are also equal. If a/b = c/d, then b/a = d/c 3. If a/b = c/d, then a/c = b/d 4. If a/b = c/d, then a+b/b = c+d/d

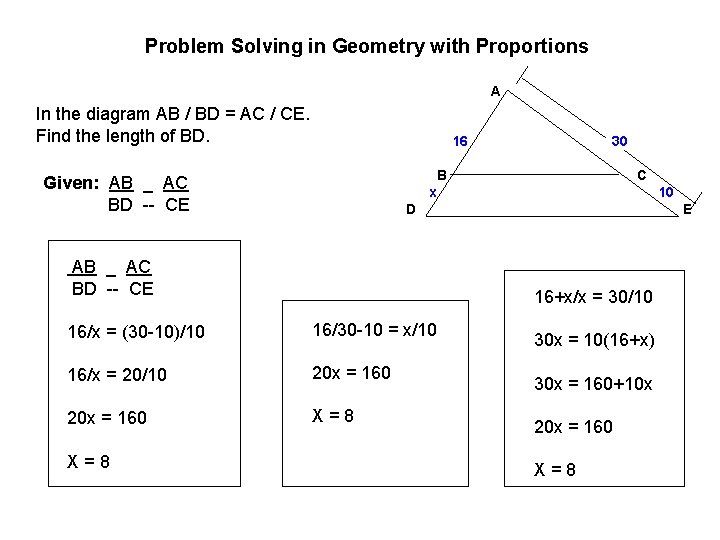
Problem Solving in Geometry with Proportions A In the diagram AB / BD = AC / CE. Find the length of BD. 16 B x Given: AB _ AC BD -- CE C 10 D AB _ AC BD -- CE E 16+x/x = 30/10 16/x = (30 -10)/10 16/30 -10 = x/10 16/x = 20/10 20 x = 160 X=8 30 30 x = 10(16+x) 30 x = 160+10 x 20 x = 160 X=8

Geometric Mean: The geometric mean of two numbers “a” and “b” is the positive number x such that: a/x = x/b. If you solve this proportion for x, through cross multiplication we find that: x 2 = a*b, therefore x = / a* b Example: What is the Geometric Mean of 8 and 18? 8/x = x/18 x 2 = 144 x = 12 Also, 8/12 = 12/18 because / 8 * 18 = / 144 = 12

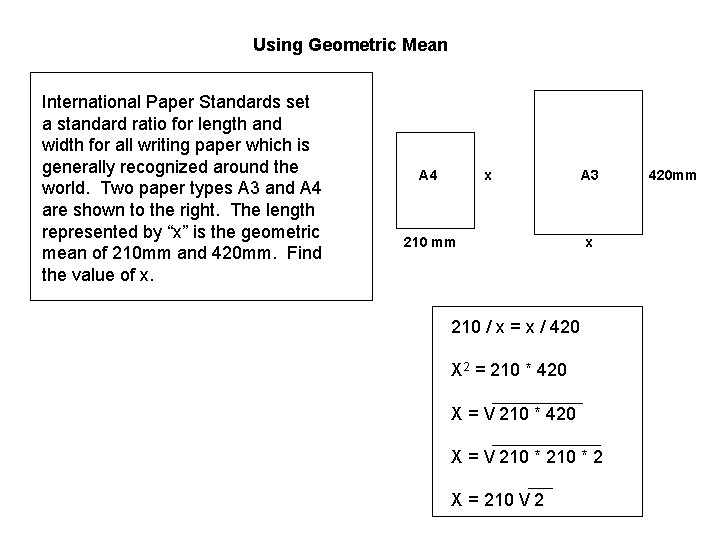
Using Geometric Mean International Paper Standards set a standard ratio for length and width for all writing paper which is generally recognized around the world. Two paper types A 3 and A 4 are shown to the right. The length represented by “x” is the geometric mean of 210 mm and 420 mm. Find the value of x. A 4 x 210 mm A 3 x 210 / x = x / 420 X 2 = 210 * 420 X = / 210 * 2 X = 210 / 2 420 mm

Using Proportions in Real Life A Scale model of the Titanic is 107. 5 inches long and 11. 25 inches wide. The Titanic itself was 882. 75 feet long. How wide was it? Width of ship = x X ft / 11. 25 in = 882. 75 ft / 107. 5 in X = (11. 25 * 882. 75) / 107. 5 X = 92. 4 Feet

Proportions and Similar Triangles R Triangle Proportionality Theorem: If a line parallel to one side of a triangle intersects the other two sides, then it divides the two sides proportionately T If TU || QS, then RT/TQ = RU/US Q Theorem 8. 6 If thee parallel lines intersect two transversals, then they divide the transversals proportionately. If r|| s and s|| t, then l and m intersect r, s, t and t, then UW/WY = VX = XZ U > S > l U W Y m X Z V t r s Theorem 8. 7 If a ray bisects an angle of a triangle , then it divides the opposite side into segments whose lengths are proportional to the lengths of the other two sides. If CD bisects <ABC, then AD/DB = CA/CB A D C B

Using Proportions in Similar Triangles C In the diagram, AB||ED, BD = 8, DC = 4, and AE = 12. What is the length of EC? 4 E D 12 8 A B G 21 M 56 Given the diagram, determine if MN || GH. H 16 ~ <3. What is In the diagram, <1 ~= <2, <2 = the length of TU? N 48 P S 9 1 Q 15 2 R 3 L 11 T U