8 1 Similarity in Right Triangles 21913 Bell

8 -1 Similarity in Right Triangles 2/19/13

Bell Work 1. Write a similarity statement comparing the two triangles. ∆ADB ~ ∆EDC Simplify. 2. 3. Solve each equation. 4. 5. 2 x 2 = 50 ± 5

Theorem 1 In a right triangle, an altitude drawn from the vertex of the right angle to the hypotenuse forms two right triangles.

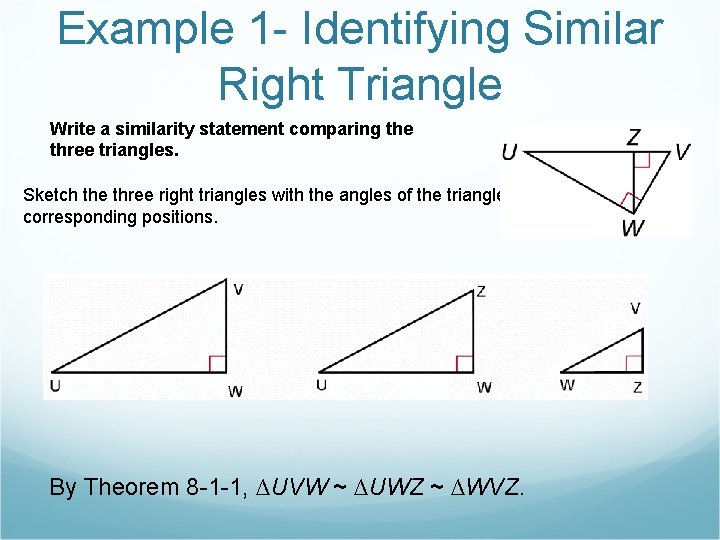
Example 1 - Identifying Similar Right Triangle Write a similarity statement comparing the three triangles. Sketch the three right triangles with the angles of the triangles in corresponding positions. By Theorem 8 -1 -1, ∆UVW ~ ∆UWZ ~ ∆WVZ.

Example 2 -On your own Write a similarity statement comparing the three triangles. Sketch the three right triangles with the angles of the triangles in corresponding positions. By Theorem 8 -1 -1, ∆LJK ~ ∆JMK ~ ∆LMJ.

Definition 1 Consider the proportion . In this case, the means of the proportion are the same number, and that number is the geometric mean of the extremes. The geometric mean of two positive numbers is the positive square root of their product. So the geometric mean of a and b is the positive number x such that , or x 2 = ab.

Example 3: Finding geometric means Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 4 and 25 Let x be the geometric mean. x 2 = (4)(25) = 100 x = 10 Def. of geometric mean Find the positive square root.

Example 4: On your own! Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 5 and 30 Let x be the geometric mean. x 2 = (5)(30) = 150 Def. of geometric mean Find the positive square root.

You can use Theorem 8 -1 -1 to write proportions comparing the side lengths of the triangles formed by the altitude to the hypotenuse of a right triangle. All the relationships in red involve geometric means.

Corollaries 1 & 2

Example 5: Finding side lengths in right triangles Find x, y, and z. h 2 = (x)(y) 62 = (x)(9) x=4 6 is the geometric mean of 9 and x. Divide both sides by 9. a 2 = (x)(c) y 2 = (4)(13) = 52 y is the geometric mean of 4 and 13. Find the positive square root. b 2 = (y)(c) z 2 = (9)(13) = 117 z is the geometric mean of 9 and 13. Find the positive square root.

REMEMBER!!! Helpful Hint Once you’ve found the unknown side lengths, you can use the Pythagorean Theorem to check your answers.

Example 6: On your own! Find u, v, and w. h 2 = (x)(y) 92 = (3)(u) u = 27 9 is the geometric mean of u and 3. Divide both sides by 3. b 2 = (y)(c) w 2 = (27 + 3)(27) w is the geometric mean of u + 3 and 27. Find the positive square root. a 2 = (x)(c) v 2 = (27 + 3)(3) v is the geometric mean of u + 3 and 3. Find the positive square root.

Example 7 To estimate the height of a Douglas fir, Jan positions herself so that her lines of sight to the top and bottom of the tree form a 90º angle. Her eyes are about 1. 6 m above the ground, and she is standing 7. 8 m from the tree. What is the height of the tree to the nearest meter? Let x be the height of the tree above eye level. h 2 = (x)(y) (7. 8)2 = 1. 6 y y = 38. 025 ≈ 38 7. 8 is the geometric mean of 1. 6 and y. Solve for y and round. The tree is about 38 + 1. 6 = 39. 6, or 40 m tall.

Example 8 -on your own! A surveyor positions himself so that his line of sight to the top of a cliff and his line of sight to the bottom form a right angle as shown. What is the height of the cliff to the nearest foot? Let x be the height of cliff above eye level. (28)2 = 5. 5 x y 142. 5 28 is the geometric mean of 5. 5 and y. Divide both sides by 5. 5. The cliff is about 142. 5 + 5. 5, or 148 ft high.