SIMILARITY THEOREMS Similarity in Triangles AngleAngle Similarity Postulate

SIMILARITY THEOREMS

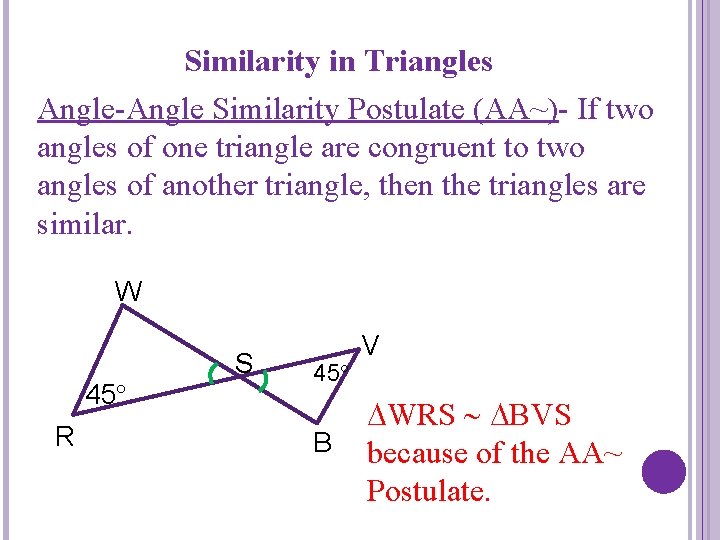
Similarity in Triangles Angle-Angle Similarity Postulate (AA~)- If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. W 45 R S 45 B V WRS BVS because of the AA~ Postulate.

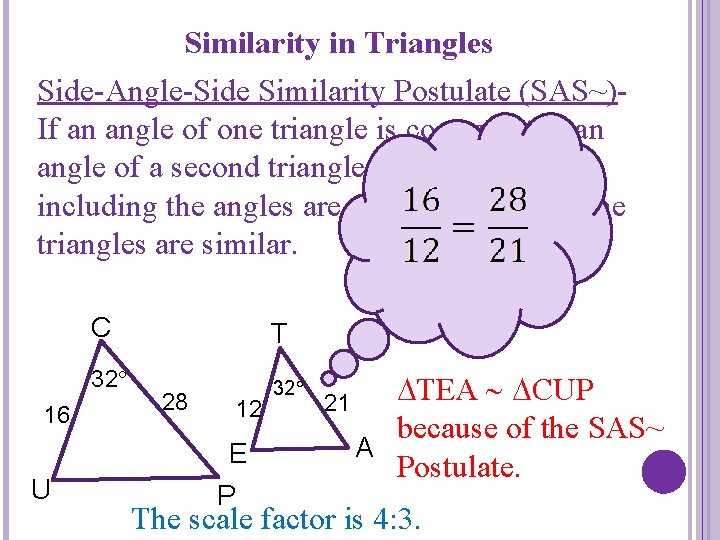
Similarity in Triangles Side-Angle-Side Similarity Postulate (SAS~)If an angle of one triangle is congruent to an angle of a second triangle, and the sides including the angles are proportional, then the triangles are similar. 16 C T 32 28 12 E U P 21 TEA CUP because of the SAS~ A Postulate. The scale factor is 4: 3.

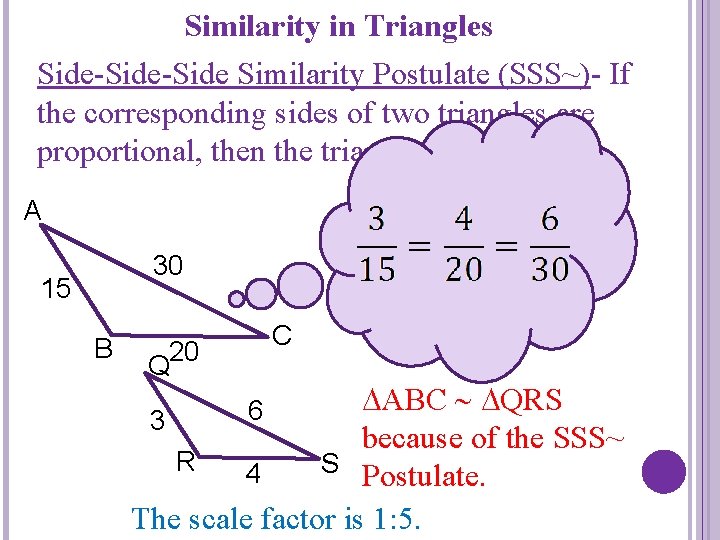
Similarity in Triangles Side-Side Similarity Postulate (SSS~)- If the corresponding sides of two triangles are proportional, then the triangles are similar. A 30 15 B C Q 20 ABC QRS 3 because of the SSS~ R S Postulate. 4 The scale factor is 1: 5. 6

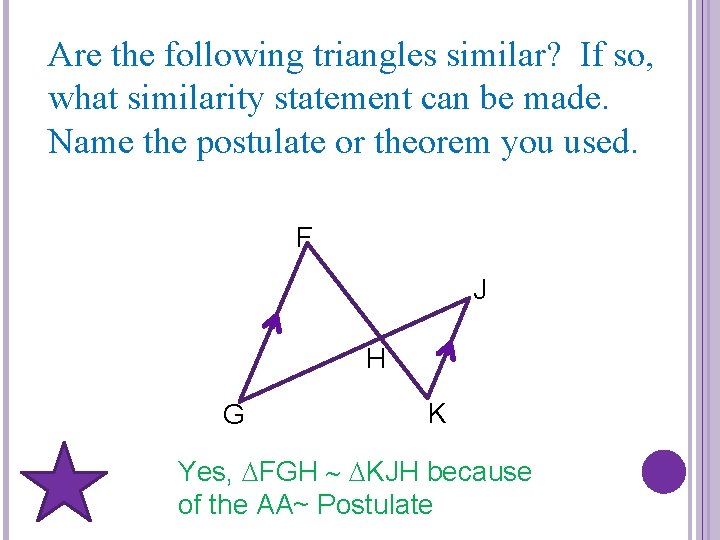
Are the following triangles similar? If so, what similarity statement can be made. Name the postulate or theorem you used. F J H G K Yes, FGH KJH because of the AA~ Postulate

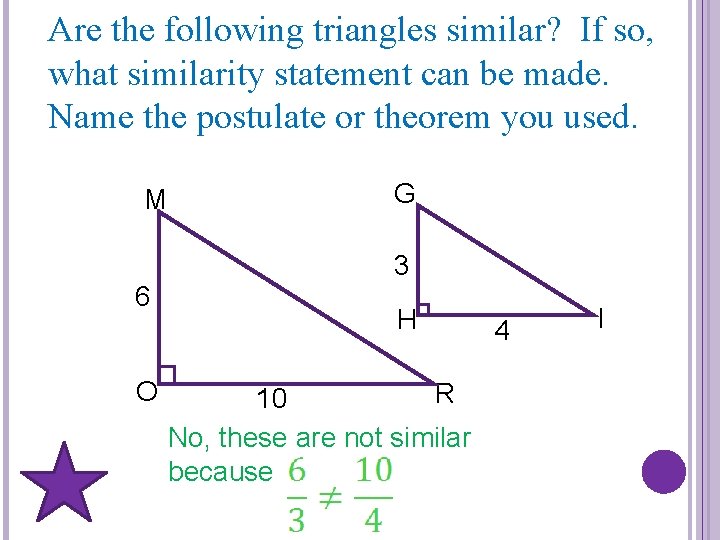
Are the following triangles similar? If so, what similarity statement can be made. Name the postulate or theorem you used. M 6 O G 3 H R 10 No, these are not similar because 4 I

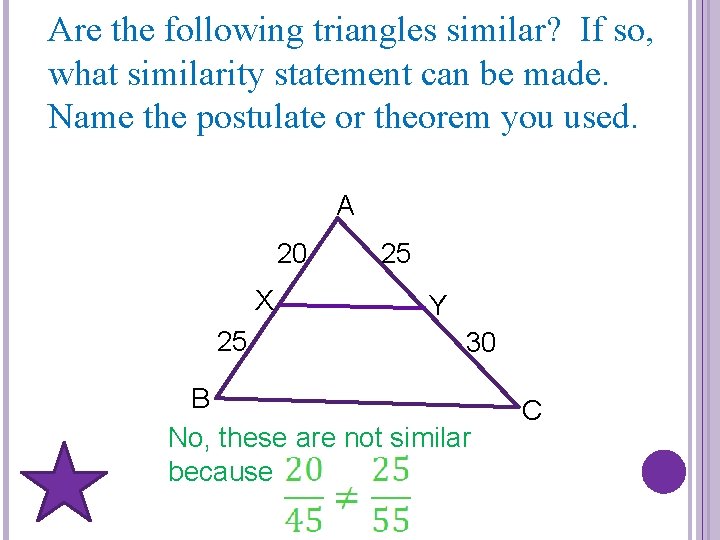
Are the following triangles similar? If so, what similarity statement can be made. Name the postulate or theorem you used. A 20 X 25 25 Y 30 B No, these are not similar because C

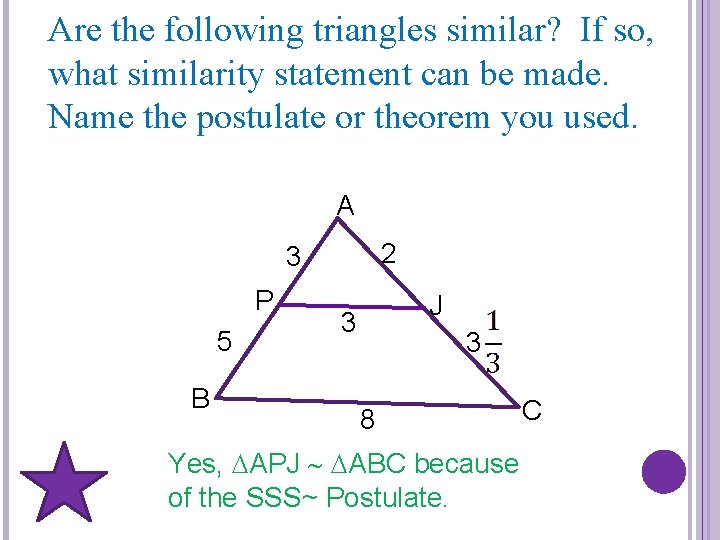
Are the following triangles similar? If so, what similarity statement can be made. Name the postulate or theorem you used. A 2 3 P 5 B J 3 3 8 Yes, APJ ABC because of the SSS~ Postulate. C

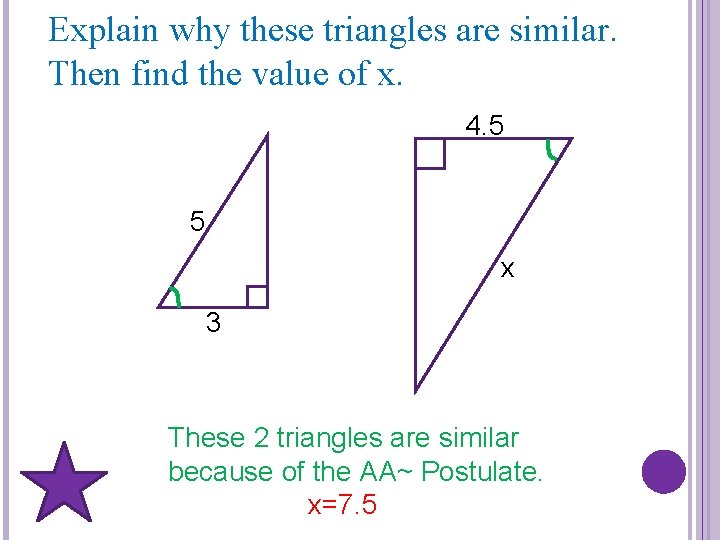
Explain why these triangles are similar. Then find the value of x. 4. 5 5 x 3 These 2 triangles are similar because of the AA~ Postulate. x=7. 5

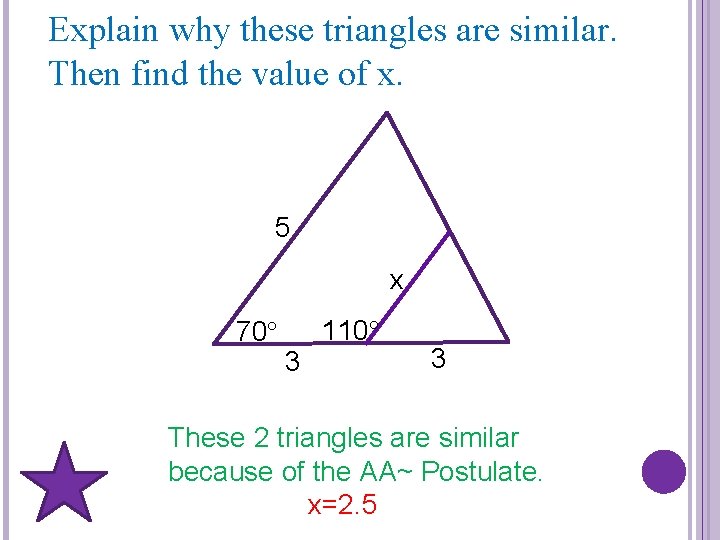
Explain why these triangles are similar. Then find the value of x. 5 x 70 3 110 3 These 2 triangles are similar because of the AA~ Postulate. x=2. 5

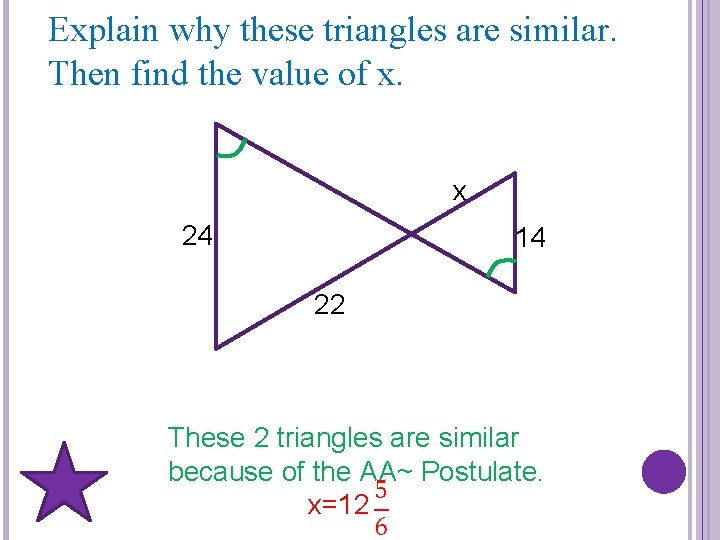
Explain why these triangles are similar. Then find the value of x. x 24 14 22 These 2 triangles are similar because of the AA~ Postulate. x=12

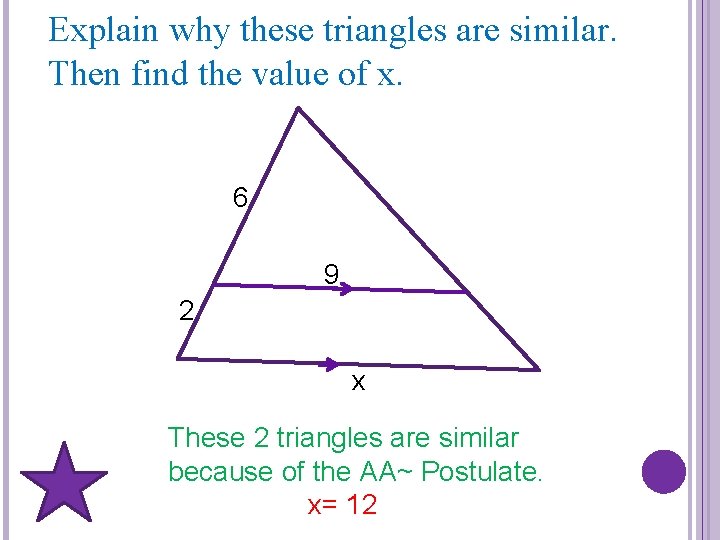
Explain why these triangles are similar. Then find the value of x. 6 9 2 x These 2 triangles are similar because of the AA~ Postulate. x= 12

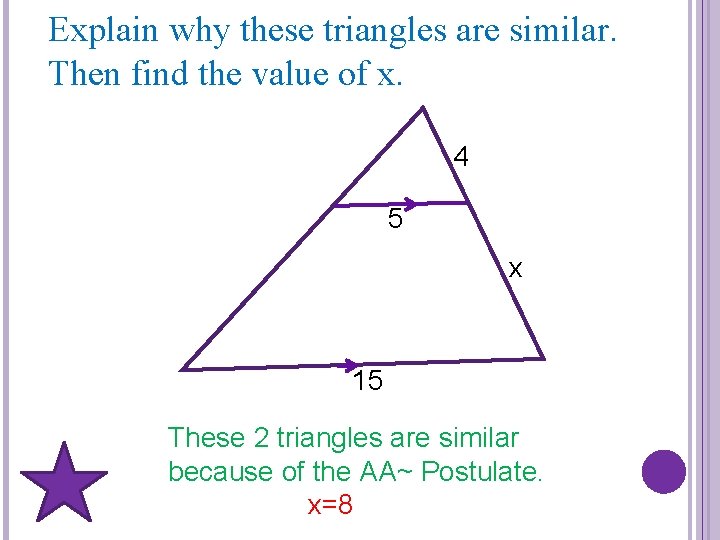
Explain why these triangles are similar. Then find the value of x. 4 5 x 15 These 2 triangles are similar because of the AA~ Postulate. x=8

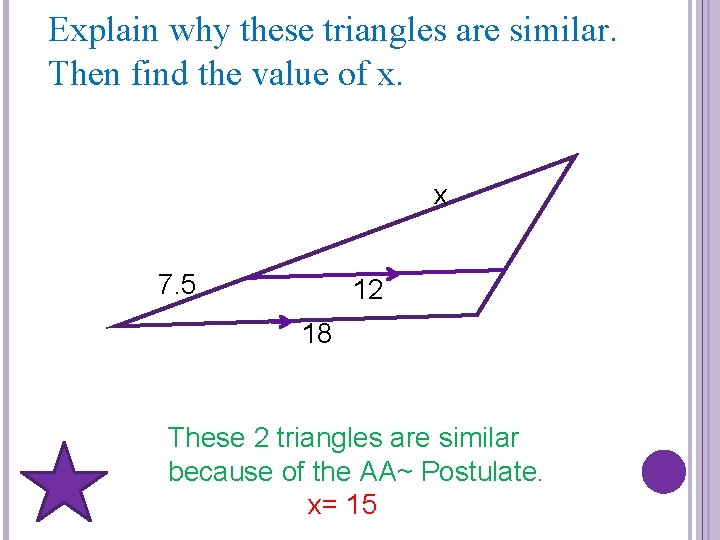
Explain why these triangles are similar. Then find the value of x. x 7. 5 12 18 These 2 triangles are similar because of the AA~ Postulate. x= 15

Please complete the Ways to Prove Triangles Similar Worksheet.

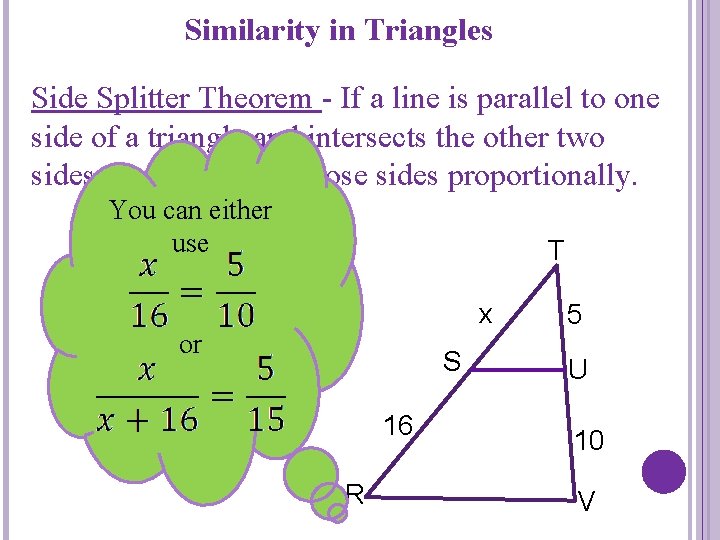
Similarity in Triangles Side Splitter Theorem - If a line is parallel to one side of a triangle and intersects the other two sides, then it divides those sides proportionally. You can either use T x or S 16 R 5 U 10 V

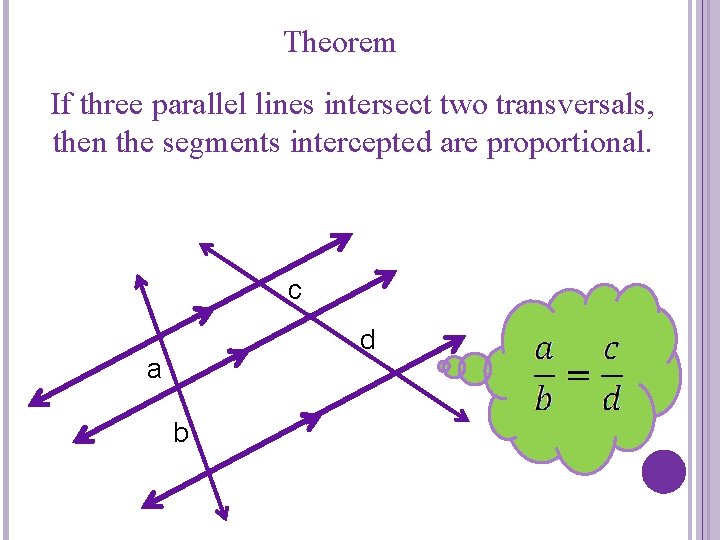
Theorem If three parallel lines intersect two transversals, then the segments intercepted are proportional. c d a b

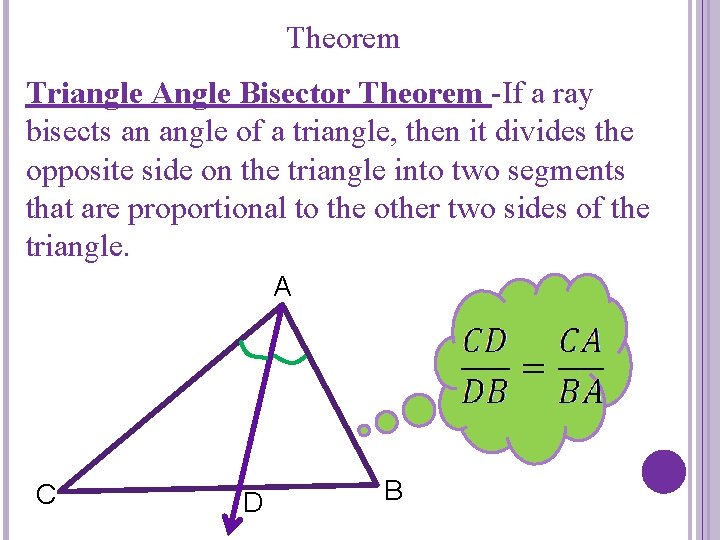
Theorem Triangle Angle Bisector Theorem -If a ray bisects an angle of a triangle, then it divides the opposite side on the triangle into two segments that are proportional to the other two sides of the triangle. A C D B

Please complete pg. 449: 1 -24, 3133.