8 1 Similarity in Right Triangles Objectives Use

8 -1 Similarity in Right Triangles Objectives Use geometric mean to find segment lengths in right triangles. Apply similarity relationships in right triangles to solve problems. Holt Geometry

8 -1 Similarity in Right Triangles Holt Geometry
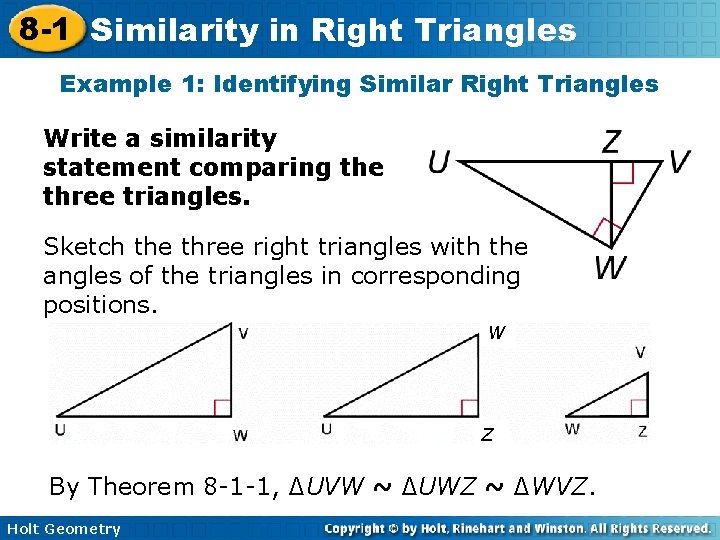
8 -1 Similarity in Right Triangles Example 1: Identifying Similar Right Triangles Write a similarity statement comparing the three triangles. Sketch the three right triangles with the angles of the triangles in corresponding positions. W Z By Theorem 8 -1 -1, ∆UVW ~ ∆UWZ ~ ∆WVZ. Holt Geometry

8 -1 Similarity in Right Triangles Consider the proportion. In this case, the means of the proportion are the same number, and that number is the geometric mean of the extremes. The geometric mean of two positive numbers is the positive square root of their product. So the geometric mean of a and b is the positive number x such that , or x 2 = ab. Holt Geometry

8 -1 Similarity in Right Triangles Example 2 A: Finding Geometric Means Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 4 and 25 Let x be the geometric mean. x 2 = (4)(25) = 100 x = 10 Holt Geometry Def. of geometric mean Find the positive square root.

8 -1 Similarity in Right Triangles Check It Out! Example 2 a Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 2 and 8 Let x be the geometric mean. x 2 = (2)(8) = 16 x=4 Holt Geometry Def. of geometric mean Find the positive square root.

8 -1 Similarity in Right Triangles Check It Out! Example 2 b Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 10 and 30 Let x be the geometric mean. x 2 = (10)(30) = 300 Def. of geometric mean Find the positive square root. Holt Geometry

8 -1 Similarity in Right Triangles Holt Geometry

8 -1 Similarity in Right Triangles Example 3: Finding Side Lengths in Right Triangles Find x, y, and z. 62 = (9)(x) x=4 6 is the geometric mean of 9 and x. Divide both sides by 9. y 2 = (4)(13) = 52 y is the geometric mean of 4 and 13. Find the positive square root. z 2 = (9)(13) = 117 z is the geometric mean of 9 and 13. Find the positive square root. Holt Geometry

8 -1 Similarity in Right Triangles Check It Out! Example 3 Find u, v, and w. 92 = (3)(u) u = 27 9 is the geometric mean of u and 3. Divide both sides by 3. w 2 = (27 + 3)(27) w is the geometric mean of u + 3 and 27. Find the positive square root. v 2 = (27 + 3)(3) Holt Geometry v is the geometric mean of u + 3 and 3. Find the positive square root.
- Slides: 10



















