9 1 Similarity in Right Triangles Warm Up

9 -1 Similarity in Right Triangles Warm Up Lesson Presentation Lesson Quiz Holt Geometry

9. 1 Similarity in Right Triangles Warm Up 1. Write a similarity statement comparing the two triangles. ∆ADB ~ ∆EDC Simplify. 2. 3. Solve each equation. 4. 5. 2 x 2 = 50 ± 5

9. 1 Similarity in Right Triangles Objectives Use geometric mean to find segment lengths in right triangles. Apply similarity relationships in right triangles to solve problems.

9. 1 Similarity in Right Triangles Vocabulary geometric mean

9. 1 Similarity in Right Triangles

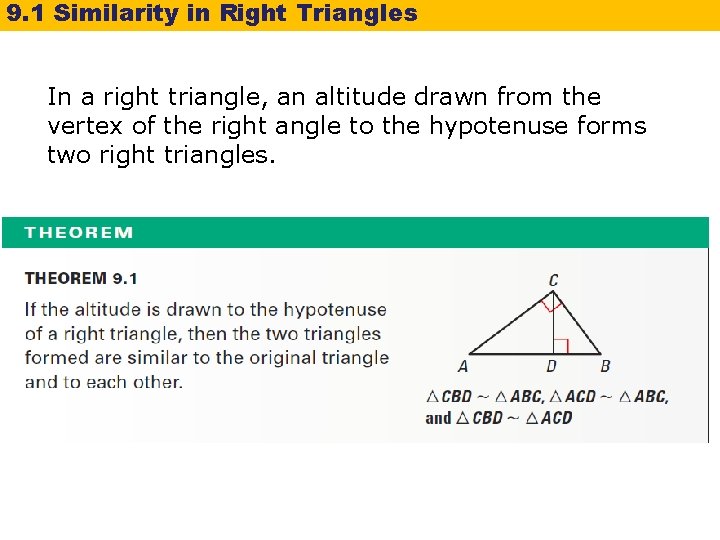
9. 1 Similarity in Right Triangles In a right triangle, an altitude drawn from the vertex of the right angle to the hypotenuse forms two right triangles.

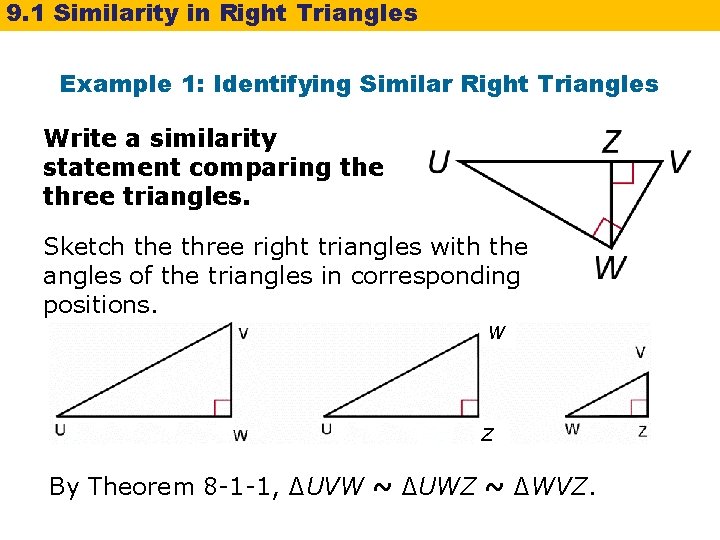
9. 1 Similarity in Right Triangles Example 1: Identifying Similar Right Triangles Write a similarity statement comparing the three triangles. Sketch the three right triangles with the angles of the triangles in corresponding positions. W Z By Theorem 8 -1 -1, ∆UVW ~ ∆UWZ ~ ∆WVZ.

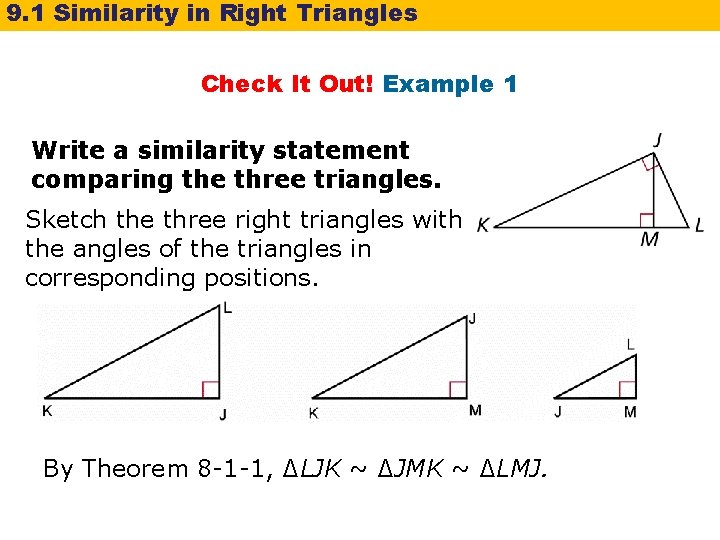
9. 1 Similarity in Right Triangles Check It Out! Example 1 Write a similarity statement comparing the three triangles. Sketch the three right triangles with the angles of the triangles in corresponding positions. By Theorem 8 -1 -1, ∆LJK ~ ∆JMK ~ ∆LMJ.

9. 1 Similarity in Right Triangles Consider the proportion. In this case, the means of the proportion are the same number, and that number is the geometric mean of the extremes. The geometric mean of two positive numbers is the positive square root of their product. So the geometric mean of a and b is the positive number x such that , or x 2 = ab.

9. 1 Similarity in Right Triangles

9. 1 Similarity in Right Triangles Example 2 A: Finding Geometric Means Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 4 and 25 Let x be the geometric mean. x 2 = (4)(25) = 100 x = 10 Def. of geometric mean Find the positive square root.

9. 1 Similarity in Right Triangles Example 2 B: Finding Geometric Means Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 5 and 30 Let x be the geometric mean. x 2 = (5)(30) = 150 Def. of geometric mean Find the positive square root.

9. 1 Similarity in Right Triangles Check It Out! Example 2 a Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 2 and 8 Let x be the geometric mean. x 2 = (2)(8) = 16 x=4 Def. of geometric mean Find the positive square root.

9. 1 Similarity in Right Triangles Check It Out! Example 2 b Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 10 and 30 Let x be the geometric mean. x 2 = (10)(30) = 300 Def. of geometric mean Find the positive square root.

9. 1 Similarity in Right Triangles Check It Out! Example 2 c Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 8 and 9 Let x be the geometric mean. x 2 = (8)(9) = 72 Def. of geometric mean Find the positive square root.

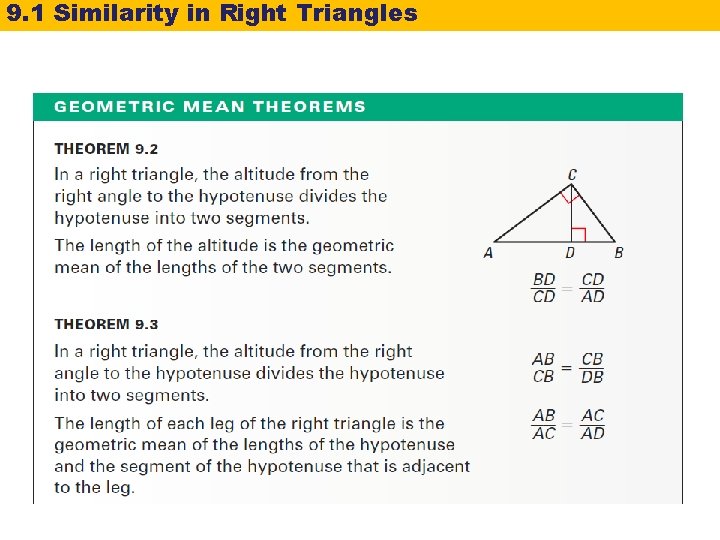
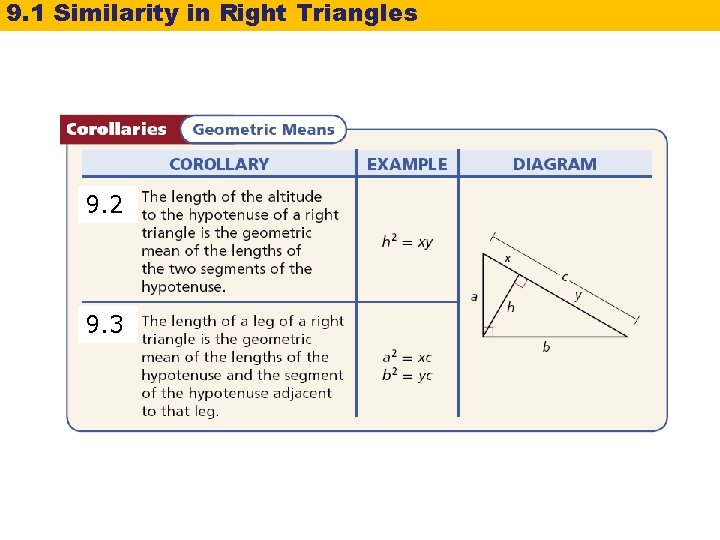
9. 1 Similarity in Right Triangles You can use Geometric Means to write proportions comparing the side lengths of the triangles formed by the altitude to the hypotenuse of a right triangle. All the relationships in red involve geometric means.

9. 1 Similarity in Right Triangles 9. 2 9. 3

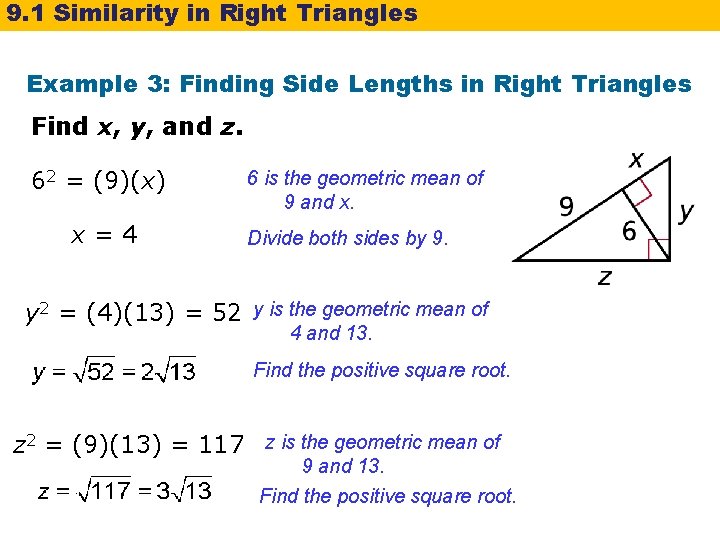
9. 1 Similarity in Right Triangles Example 3: Finding Side Lengths in Right Triangles Find x, y, and z. 62 = (9)(x) x=4 6 is the geometric mean of 9 and x. Divide both sides by 9. y 2 = (4)(13) = 52 y is the geometric mean of 4 and 13. Find the positive square root. z 2 = (9)(13) = 117 z is the geometric mean of 9 and 13. Find the positive square root.

9. 1 Similarity in Right Triangles Helpful Hint Once you’ve found the unknown side lengths, you can use the Pythagorean Theorem to check your answers.

9. 1 Similarity in Right Triangles Check It Out! Example 3 Find u, v, and w. 92 = (3)(u) u = 27 9 is the geometric mean of u and 3. Divide both sides by 3. w 2 = (27 + 3)(27) w is the geometric mean of u + 3 and 27. Find the positive square root. v 2 = (27 + 3)(3) v is the geometric mean of u + 3 and 3. Find the positive square root.

9. 1 Similarity in Right Triangles Example 4: Measurement Application To estimate the height of a Douglas fir, Jan positions herself so that her lines of sight to the top and bottom of the tree form a 90º angle. Her eyes are about 1. 6 m above the ground, and she is standing 7. 8 m from the tree. What is the height of the tree to the nearest meter?

9. 1 Similarity in Right Triangles Example 4 Continued Let x be the height of the tree above eye level. (7. 8)2 = 1. 6 x 7. 8 is the geometric mean of 1. 6 and x. x = 38. 025 ≈ 38 Solve for x and round. The tree is about 38 + 1. 6 = 39. 6, or 40 m tall.

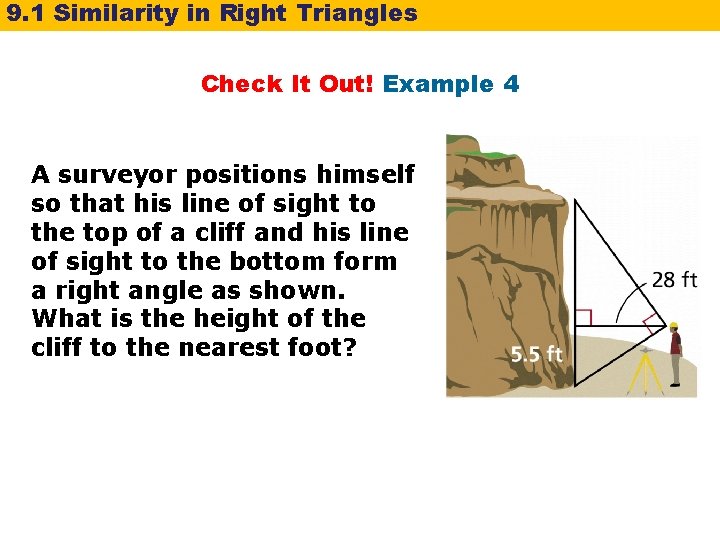
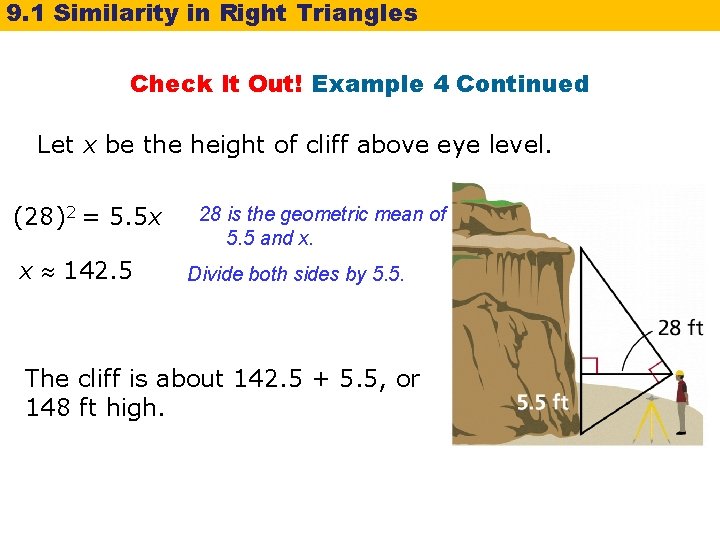
9. 1 Similarity in Right Triangles Check It Out! Example 4 A surveyor positions himself so that his line of sight to the top of a cliff and his line of sight to the bottom form a right angle as shown. What is the height of the cliff to the nearest foot?

9. 1 Similarity in Right Triangles Check It Out! Example 4 Continued Let x be the height of cliff above eye level. (28)2 = 5. 5 x x 142. 5 28 is the geometric mean of 5. 5 and x. Divide both sides by 5. 5. The cliff is about 142. 5 + 5. 5, or 148 ft high.

9. 1 Similarity in Right Triangles Lesson Quiz: Part I Find the geometric mean of each pair of numbers. If necessary, give the answer in simplest radical form. 1. 8 and 18 2. 6 and 15 12

9. 1 Similarity in Right Triangles Lesson Quiz: Part II For Items 3– 6, use ∆RST. 3. Write a similarity statement comparing the three triangles. ∆RST ~ ∆RPS ~ ∆SPT 4. If PS = 6 and PT = 9, find PR. 4 5. If TP = 24 and PR = 6, find RS. 6. Complete the equation (ST)2 = (TP + PR)(? ). TP