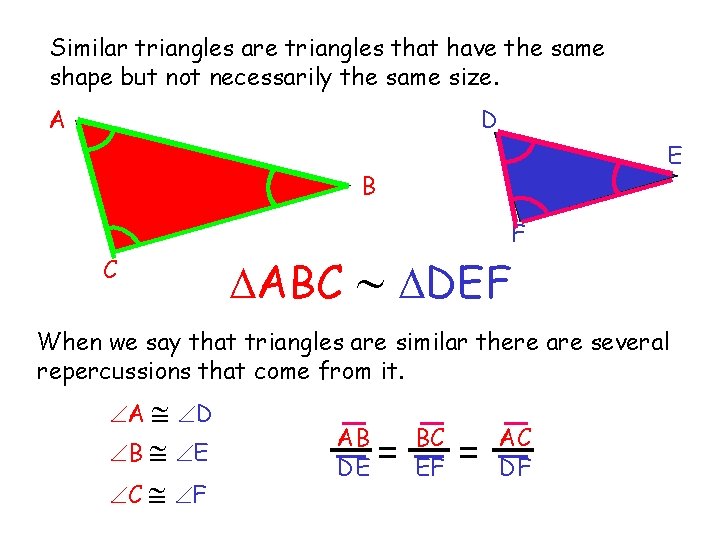
Similar triangles are triangles that have the same

Similar triangles are triangles that have the same shape but not necessarily the same size. A D E B F C ABC DEF When we say that triangles are similar there are several repercussions that come from it. A D B E C F AB DE = BC EF = AC DF

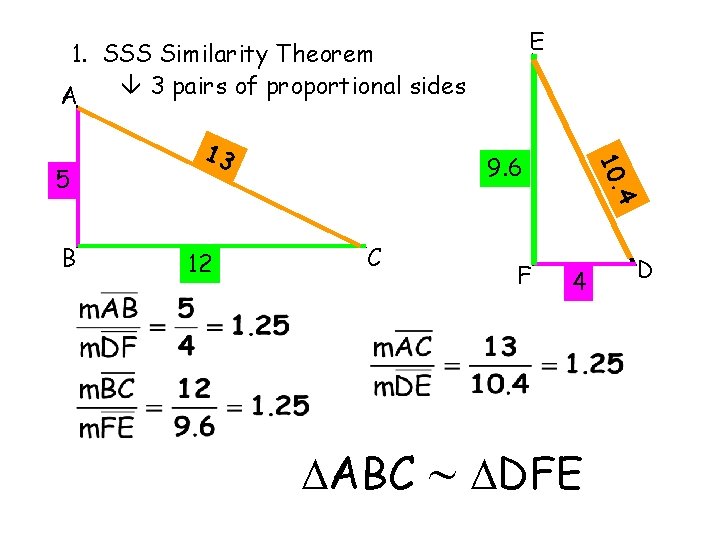
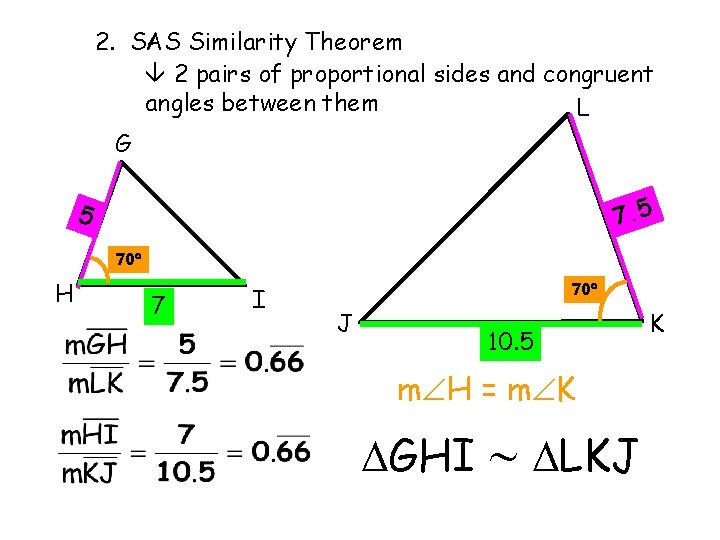
Six of those statements are true as a result of the similarity of the two triangles. However, if we need to prove that a pair of triangles are similar how many of those statements do we need? Because we are working with triangles and the measure of the angles and sides are dependent on each other. We do not need all six. There are three special combinations that we can use to prove similarity of triangles. 1. SSS Similarity Theorem 3 pairs of proportional sides 2. SAS Similarity Theorem 2 pairs of proportional sides and congruent angles between them 3. AA Similarity Theorem 2 pairs of congruent angles

E 1. SSS Similarity Theorem 3 pairs of proportional sides A . 4 B 9. 6 10 5 13 12 C ABC F 4 DFE D

2. SAS Similarity Theorem 2 pairs of proportional sides and congruent angles between them L G 7. 5 5 70 H 7 I 70 J 10. 5 m H = m K GHI LKJ K

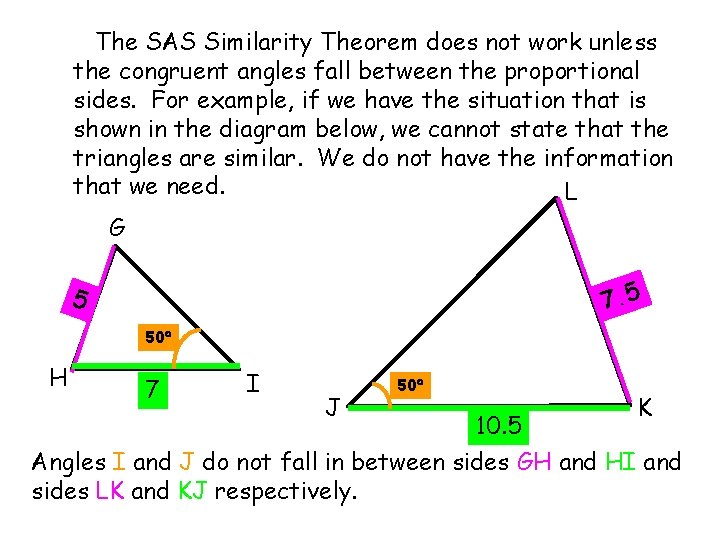
The SAS Similarity Theorem does not work unless the congruent angles fall between the proportional sides. For example, if we have the situation that is shown in the diagram below, we cannot state that the triangles are similar. We do not have the information that we need. L G 7. 5 5 50 H 7 I J 50 10. 5 K Angles I and J do not fall in between sides GH and HI and sides LK and KJ respectively.

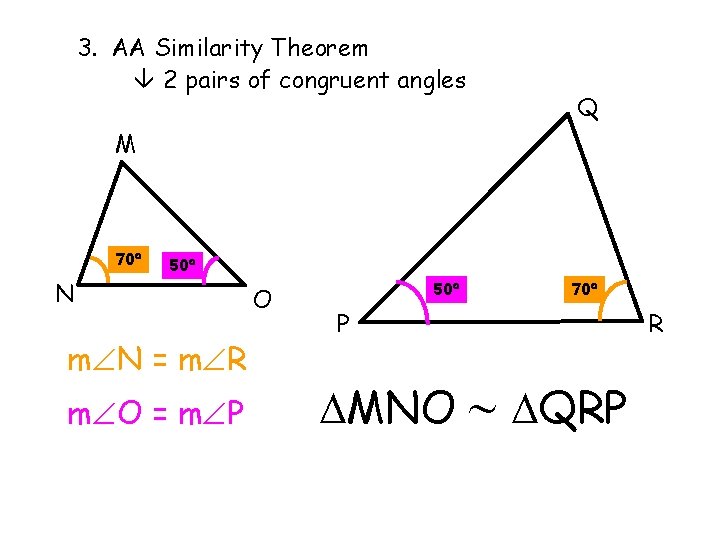
3. AA Similarity Theorem 2 pairs of congruent angles Q M 70 50 N m N = m R m O = m P O 50 70 P MNO R QRP

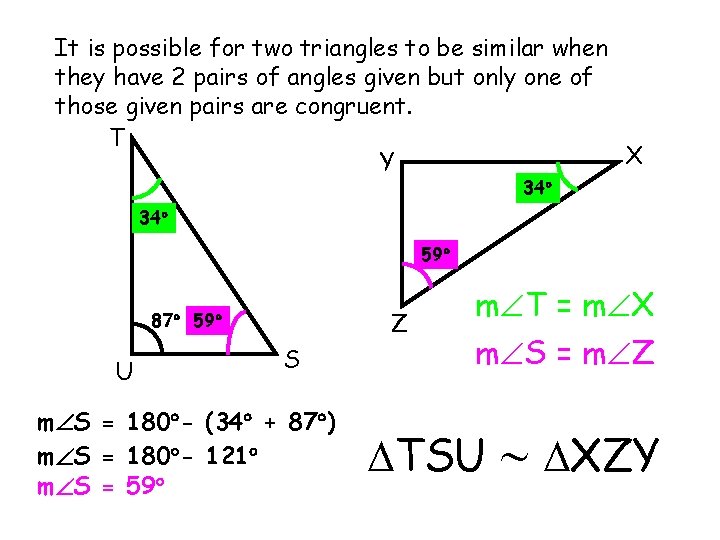
It is possible for two triangles to be similar when they have 2 pairs of angles given but only one of those given pairs are congruent. T X Y 34 59 59 Z 87 59 U S m S = 180 - (34 + 87 ) m S = 180 - 121 m S = 59 m T = m X m S = m Z TSU XZY

КОf. Нin l Е APU KAT la a σ Ц ο n d λ if έ τen ﭙ ﺎ ﺎﻴ SAN to fini e h T ﻦ sof