Right Triangles Right Triangles n A triangle with

+ Right Triangles

+ Right Triangles n A triangle with a right angle in it n Scalene Right Triangle- One right angle, two other unequal angles, no equal sides n Isosceles Right Triangle- One right angle, two other equal angles, two equal sides

+ n Pythagorean Theorem In a right angled triangle: the square of the hypotenuse is equal to the sum of the squares of the other two sides. n Hypotenuse- the longest side of the right triangle and is always opposite of the right angle n Leg(s)- the sides of the right triangle that are on either side of the right angle

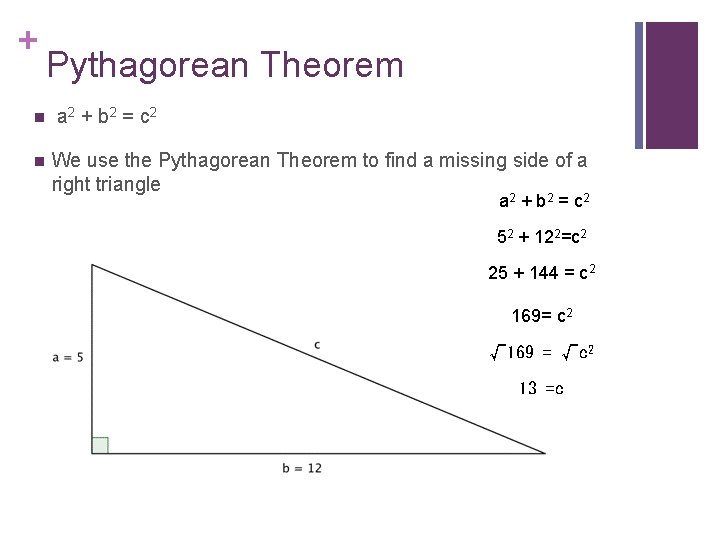
+ n Pythagorean Theorem a 2 + b 2 = c 2 n A is a leg n B is a leg n C is the hypotenuse

+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle a 2 + b 2 = c 2 52 + 122=c 2 25 + 144 = c 2 169= c 2 √ 169 = √c 2 13 =c

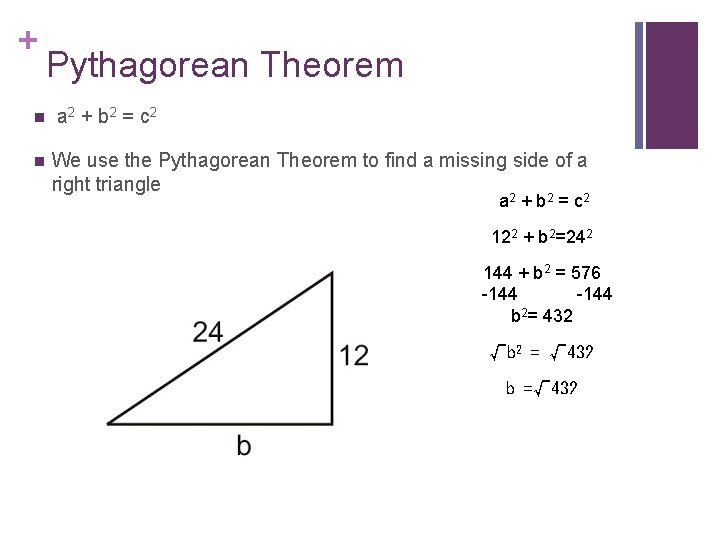
+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle a 2 + b 2 = c 2 122 + b 2=242 144 + b 2 = 576 -144 b 2= 432 √b 2 = √ 432 b =√ 432

+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle a 2 + b 2 = c 2 72 + b 2=92 49 + b 2 = 81 -49 b 2= 32 √b 2 = √ 32 b =√ 32

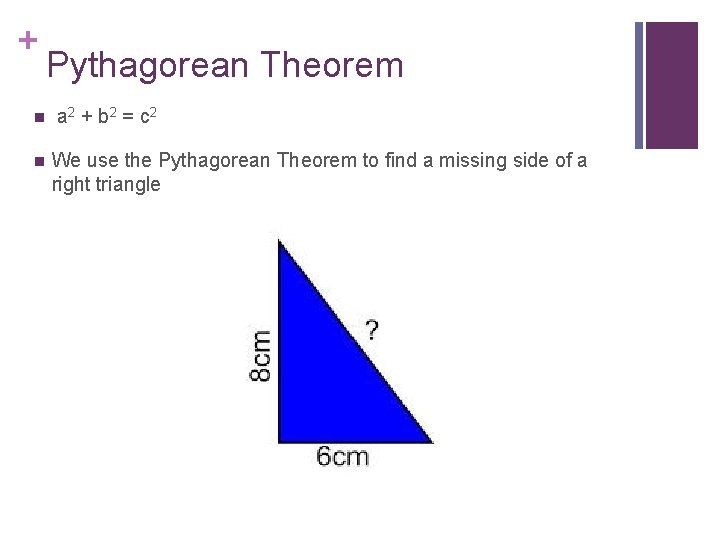
+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle

+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle

+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle

+ Practice n Work on the following worksheet!

+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle Maria walked 3 km west and 4 km south. Calculate how far she is from her starting point. 3 km 4 km ? km a 2 + b 2 = c 2 32 + 4 2 = c 2 9 + 16 = c 2 25 = c 2 √ 25 = √ c 2 5=c

+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle Lena’s guest house is 15 m long and 12 m wide. How long is the diagonal of the house? 12 km 15 km ? km a 2 + b 2 = c 2 152 + 122 = c 2 225 + 144 = c 2 369 = c 2 √ 369 = √ c 2 √ 369 = c

+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle David must install fencing around a lot that is shaped like a right triangle. The side of the lot that runs east-west is 200 ft long. The side of the lot that runs north-south is 125 ft long. Calculate how many feet of fencing he will need to surround the entire lot. 200 ft 125 ft ? ft a 2 + b 2 = c 2 1252 + 2002 = c 2 15, 625 + 40, 000= c 2 55, 625 = c 2 √ 55, 625= √ c 2 √ 55, 625= c

+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle David must install fencing around a lot that is shaped like a right triangle. The side of the lot that runs east-west is 200 ft long. The side of the lot that runs north-south is 125 ft long. Calculate how many feet of fencing he will need to surround the entire lot. 200 ft 125 ft ? ft a 2 + b 2 = c 2 1252 + 2002 = c 2 15, 625 + 40, 000= c 2 55, 625 = c 2 √ 55, 625= √ c 2 √ 55, 625= c

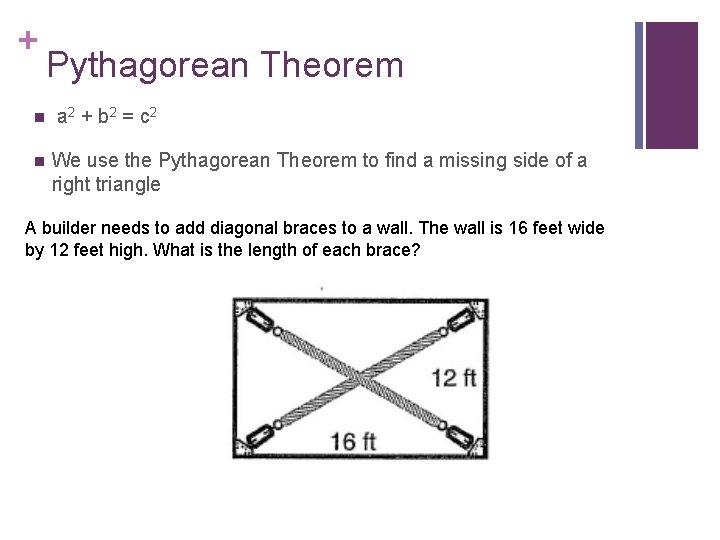
+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle A builder needs to add diagonal braces to a wall. The wall is 16 feet wide by 12 feet high. What is the length of each brace?

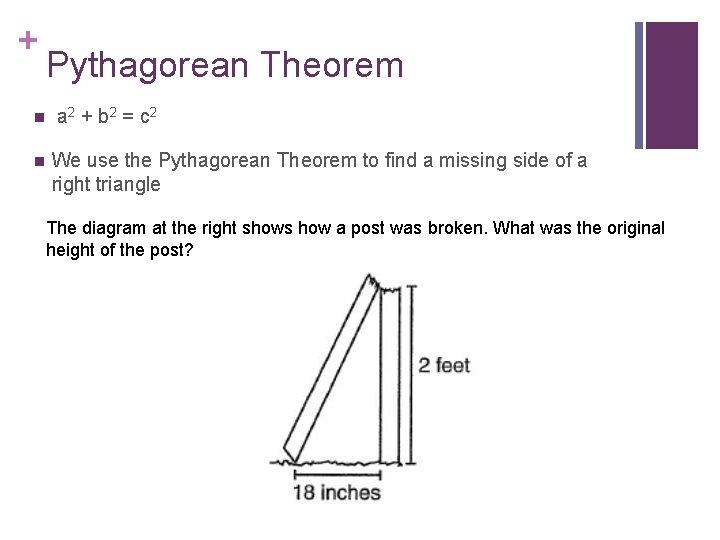
+ n n Pythagorean Theorem a 2 + b 2 = c 2 We use the Pythagorean Theorem to find a missing side of a right triangle The diagram at the right shows how a post was broken. What was the original height of the post?