EXAMPLE 1 Use the AA Similarity Postulate Determine





- Slides: 8

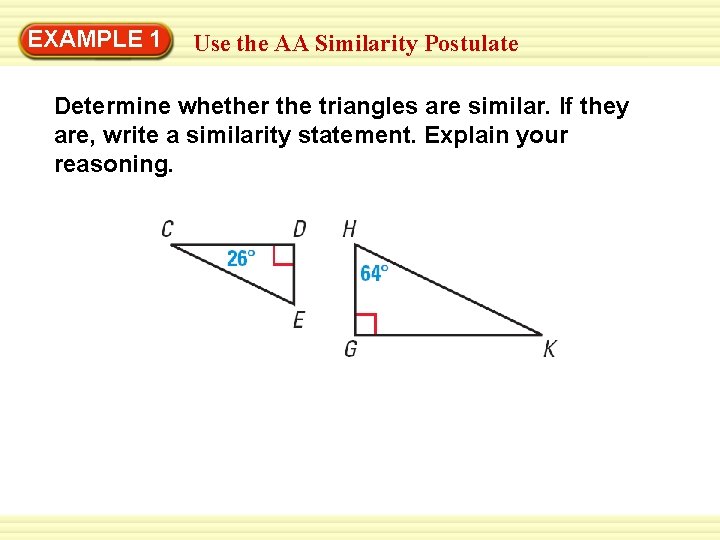
EXAMPLE 1 Use the AA Similarity Postulate Determine whether the triangles are similar. If they are, write a similarity statement. Explain your reasoning.

EXAMPLE 1 Use the AA Similarity Postulate SOLUTION Because they are both right angles, congruent. D and G are By the Triangle Sum Theorem, 26° + 90° + m E = 180°, so m E = 64°. Therefore, E and H are congruent. ANSWER So, ∆CDE ~ ∆KGH by the AA Similarity Postulate.

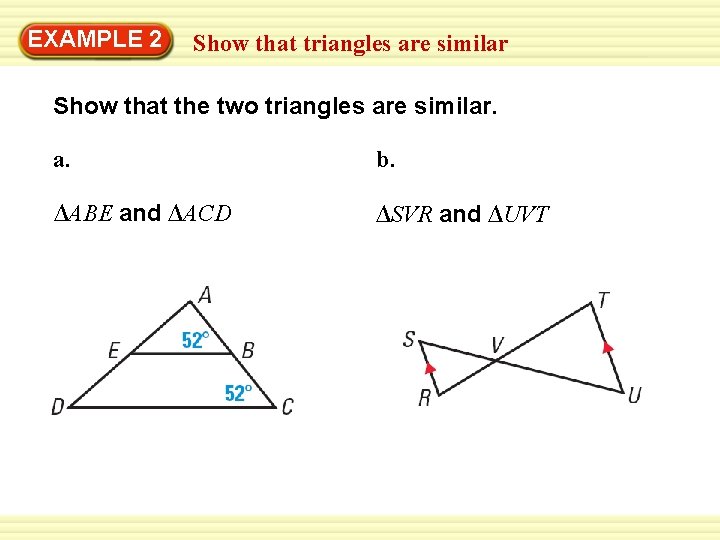
EXAMPLE 2 Show that triangles are similar Show that the two triangles are similar. a. b. ∆ABE and ∆ACD ∆SVR and ∆UVT

EXAMPLE 2 Show that triangles are similar SOLUTION a. You may find it helpful to redraw the triangles separately. Because m ABE and m C both equal 52°, ABE C. By the Reflexive Property, A ANSWER So, ∆ ABE ~ ∆ ACD by the AA Similarity Postulate. A.

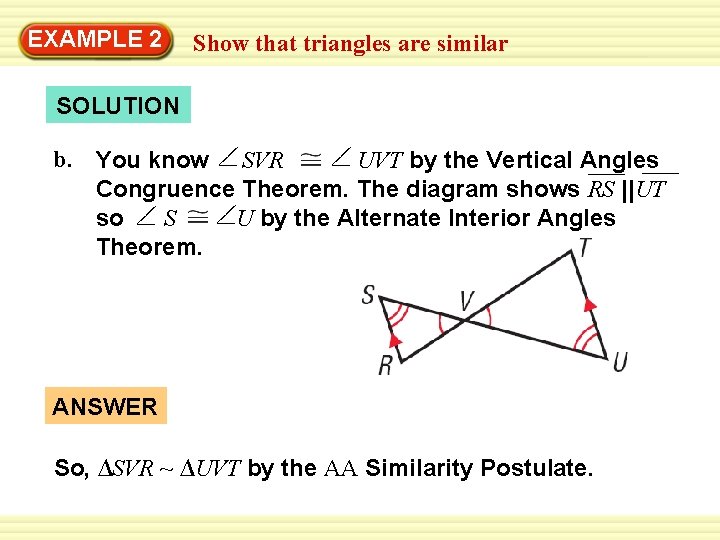
EXAMPLE 2 Show that triangles are similar SOLUTION b. You know SVR UVT by the Vertical Angles Congruence Theorem. The diagram shows RS ||UT so S U by the Alternate Interior Angles Theorem. ANSWER So, ∆SVR ~ ∆UVT by the AA Similarity Postulate.

GUIDED PRACTICE for Examples 1 and 2 Show that the triangles are similar. Write a similarity statement. 1. ∆FGH and ∆RQS ANSWER In each triangle all three angles measure 60°, so by the AA similarity postulate, the triangles are similar ∆FGH ~ ∆QRS.

GUIDED PRACTICE for Examples 1 and 2 Show that the triangles are similar. Write a similarity statement. 2. ∆CDF and ∆DEF ANSWER Since m CDF = 58° by the Triangle Sum Theorem and m DFE = 90° by the Linear Pair Postulate the two triangles are similar by the AA Similarity Postulate; ∆CDF ~ ∆DEF.

GUIDED PRACTICE 3. for Examples 1 and 2 Reasoning Suppose in Example 2, part (b), SR triangles still be similar? Explain. TU. Could the ANSWER Yes; if S T, the triangles are similar by the AA Similarity Postulate.