Signali i sustavi Ekvivalencija vremenski kontinuiranog i diskretnog































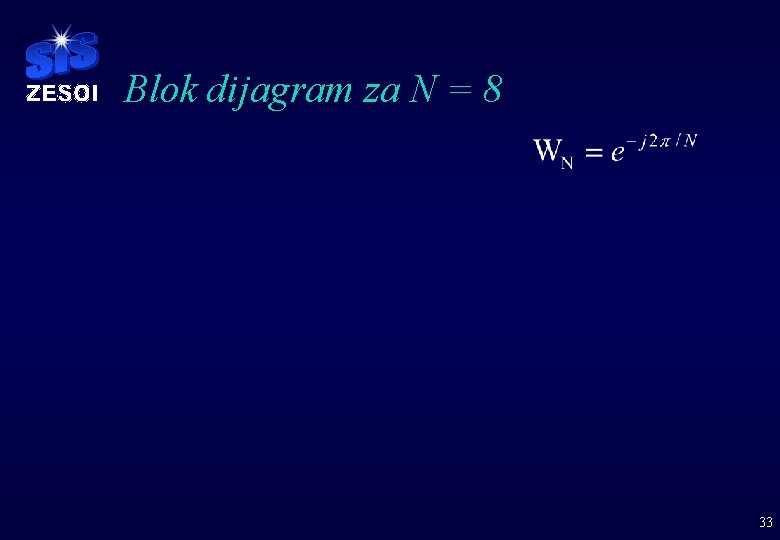





- Slides: 39

Signali i sustavi Ekvivalencija vremenski kontinuiranog i diskretnog signala i sustava

Vremenska diskretizacija tipkanjem kontinuiranog signala § Postupak uzimanja uzoraka ili tipkanja kontinuiranog signala f možemo matematički modelirati kao pridruživanje funkciji f niza impulsa f *, čiji intenzitet je proporcionalan trenutnim vrijednostima kontinuiranog signala. f *(t) = ST{f(t)} § Možemo to interpretirati kao modulaciju impulsnog niza funkcijom f, tj. 2

Vremenska diskretizacija tipkanjem kontinuiranog signala 3

Vremenska diskretizacija tipkanjem kontinuiranog signala § Zbog svojstva delta funkcije da vadi vrijednost kontinuirane funkcije f(t) na mjestu diskontinuiteta t - k. T = 0, tj. tk = k. T, može se napisati i u obliku: 4

Vremenska diskretizacija tipkanjem kontinuiranog signala § Uvjete ekvivalencije kontinuiranog i diskretnog signala dobivenog postupkom otipkavanja najlakše je pratiti preko njihovih spektara. § Neka signal f ima spektar: § Iz spektra F se može doći do same funkcije f inverznim Fourierovim integralom: 5

Vremenska diskretizacija tipkanjem kontinuiranog signala § Periodičan niz d. T nastao ponavljanjem delta funkcije svakih T, kao svaka periodična funkcija se dade predstaviti Fourierovim redom, gdje su amplitude dane s: § Odatle: 6

Vremenska diskretizacija tipkanjem kontinuiranog signala § Spektar otipkanog signala f * dan je s: § Zamjenom redoslijeda sumacije i integracije dobivamo: § Integral je spektar funkcije f, ali pomaknut za nw 0, pa izlazi: 7

Vremenska diskretizacija tipkanjem kontinuiranog signala § Spektar F* otipkanog signala f * je periodično ponavljani spektar F kontinuiranog signala. § Pretpostavimo da je spektar F frekvencijski ograničen F(w) = 0 za |w| > wg. § Različite frekvencije tipkanja signala w 0 = 2 p/T mogu u spektru F*(w) izazvati različite rezultate zavisno od toga da li je w 0 - wg > wg ili w 0 - wg < wg odnosno: w 0 > 2 wg, w 0 < 2 wg. 8

Vremenska diskretizacija tipkanjem kontinuiranog signala Preklapanje sekcija spektra (engl. “aliasing”). 9

Zaključak § Diskretni se signal može smatrati ekvivalentnim kontinuiranom samo ako je moguće rekonstruirati izvorni signal f iz otipkanog f *, odnosno ako se iz spektra F* može dobiti originalni F. Postupak rekonstrukcije pretpostavlja izdvajanje osnovne sekcije spektra filtriranjem. § To će biti moguće načiniti bez pogreške samo ako je spektar F ograničen na wg, te ako je frekvencija otipkavanja w 0 > 2 wg. 10

Obnavljanje ili rekonstrukcija kontinuiranog signala iz diskretnog § Periodični spektar F* može se dobiti i iz § U dobivenom izrazu se može prepoznati Fourierov red za periodični spektar F*. 11

Obnavljanje ili rekonstrukcija kontinuiranog signala iz diskretnog § Da bi se dobila osnovna sekcija spektra Fc odnosno po mogućnosti F , potrebno je izvršiti filtraciju F* s filtrom frekvencijske karakteristike Hr , Fc(w) = F*(w) Hr(w). 12

Obnavljanje ili rekonstrukcija kontinuiranog signala iz diskretnog § Pretpostavimo za Hr idealan filter § Impulsni odziv je § Neka je frekvencija otipkavanja w 0 > 2 wg, tako da unutar pojasa ponavljanja (-w 0/2, w 0/2), nema preklapanja sekcija spektra. § Tada je: 13

Obnavljanje ili rekonstrukcija kontinuiranog signala iz diskretnog § Inverznom Fourierovom transformacijom spektra F dobivamo: 14

Obnavljanje ili rekonstrukcija kontinuiranog signala iz diskretnog § Vidimo da je f(t) dobiven iz uzoraka f(k. T) interpolacijom s funkcijom: § Iz gornjega izvoda slijedi da je kontinuirana funkcija f, koja ima frekvencijski omeđen spektar (F(w) = 0 za |w | > w 0/2), jednoznačno određena svojim trenutnim vrijednostima u jednoliko raspoređenim trenucima tk = k. T = 2 p k / w 0. Interpolacijska funkcija predstavlja impulsni odziv idealnog filtra. 15

Filtar ima nekauzalan odziv i prema tome je neostvariv. 16

Interpolator nultog reda 17

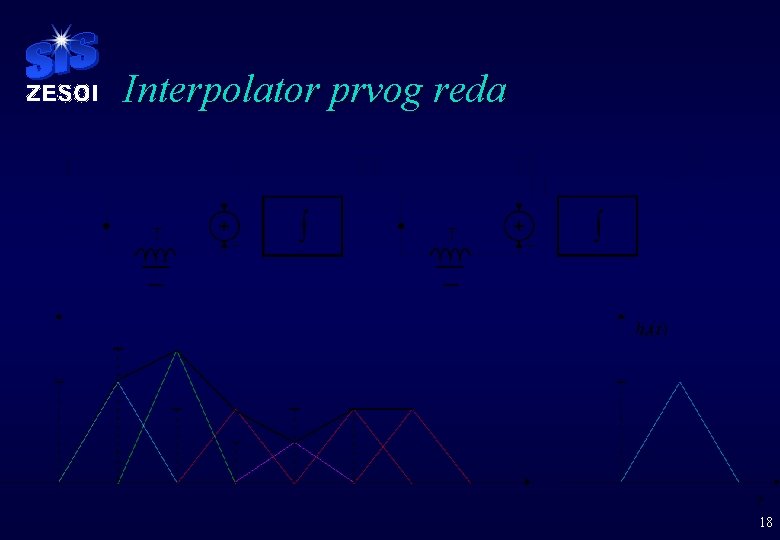
Interpolator prvog reda 18

Antialiasing filtri § Greška uslijed aliasinga § Konstantna amplituda: Butherworth, Chebyshev, Cauer. § Linearna faza: Bessel. 19

Diskretizacija spektra kontinuiranog signala § Analognim pristupom može se provesti diskretizacija kontinuranog spektra nekog signala Fd(w ) = SW{F(w )}, § Signal u vremenu fd koji odgovara otipkanom spektru, dan je s § Otipkavanje spektra daje fd periodično ponavljanu funkciju f. 20

Diskretizacija spektra kontinuiranog signala § Ako je funkcija f takva da je njeno trajanje 2 tg < t 0 neće nastupiti preklapanje (aliasing) u vremenu. § Izvorni signal moći će se dobiti pomoću vremenskog otvora množenjem fd s idealnim vremenskim otvorom f(t) = fd(t) w(t) § F(w) se može jednoznačno dobiti iz svojih uzoraka F(n. W), interpolacijom § Kontinuirani spektar signala konačnog trajanja (f(t) = 0 za |t| > t 0/2) jednoznačno je određen svojim uzorcima na frekvencijama wn = n. W. 21

Dimenzionalnost signala § Otipkavanje signala ® ponavljanje spektra s Wp = w 0. (aliasing u FD) § Otipkavanje spektra ® ponavljanje signala s Tp = t 0. (aliasing u VD) relativna greška u VD relativna greška u FD § Greške se mogu ocijeniti poznavanjem brzine opadanja signala i spektra za t > Tp / 2 odnosno w > Wp / 2. 22

Dimenzionalnost signala § Uz specificiranu dozvoljenu grešku aliasinga u FD i VD dobivamo Tp i Wp - trajanje i širinu pojasa signala § potreban broj uzoraka u VD § potreban broj uzoraka u FD § dimenzija signala § Dimenzionalnost signala je važna u teoriji, a ima direktnu primjenu u diskretnoj Fourierovoj transformaciji. 23

Diskretna Fourierova transformacija § DFT se koristi za numeričko određivanje spektra signala. § Signal i njegov spektar treba predstaviti uzorcima odnosno otipkati. § To s druge strane znači da će se otipkani signal i njegov otipkani spektar periodički produžiti. § Uzmimo signal f i ponovimo ga periodički svakih Tp i predstavimo ga Fourierovim redom 24

Diskretna Fourierova transformacija § Otipkavanje tog signala može se provesti nizom delta funkcija § Odakle iz jednakosti 2 p / T = NW slijedi: 25

Diskretna Fourierova transformacija § Budući da je eksponencijala periodična funkcija mogu se skupiti komponente, koje množi ista eksponencijala. § Uvođenjem izlazi § Beskonačna suma se može prikazati sumom od samo N različitih eksponencijala. 26

Diskretna Fourierova transformacija §U se nalaze zrcaljene amplitude svih komponenti izvan pojasa Wp = NW i zbrajaju s onim unutar pojasa. § su dakle uzorci periodički produženog spektra (Wp) jednog periodički produženog signala (Tp). § Odnos između uzoraka i u potpunosti je određen tzv. diskretnom Fourierovom transformacijom (DFT). § Potrebni broj uzoraka N u bilo kojoj od domena je dan dimenzionalnošću signala. 27

Diskretna Fourierova transformacija § Uzorci spektra slijede također iz sumacije, koju možemo dobiti ako izvorni izraz pomnožimo s i sumiramo preko N vremenskih uzoraka § Suma eksponencijala po k daje za n = r + m. N iznos N a inače 0, kako se može zaključiti iz izraza za sumu geometrijskog reda 28

Diskretna Fourierova transformacija § Može se napisati konačno DFT par § Koeficijent 1/N se nekada pridružuje drugoj sumaciji koja se naziva inverznom DFT. Izrazi daju jednoznačnu vezu između nizova i periodičnih s periodom N. 29

Diskretna Fourierova transformacija § DFT je numerički postupak. § Koliko točno postupak predstavlja Fourierovu transformaciju izvornog kontinuiranog signala f u spektar F, zavisi kako je pokazano ranije od izabranog Tp i Wp , te brzine opadanja signala i spektra za t > Tp / 2 i w > Wp / 2. 30

Brza Fourierova transformacija § Brzom Fourierovom transformacijom (FFT) naziva se skupina efikasnih postupaka za računanje DFT-a. § Direktno računanje jednog uzorka traži N kompleksnih množenja s i. N kompleksih zbrajanja. § Buduće da treba izračunati N uzoraka odnosn pri inverznoj transformaciji (IDFT) trebat će N 2 množenja. § FFT postupci omogućuju računanje DFT-a uz znantno manji broj množenja proporcionalan s N 31 log 2 N.

Brza Fourierova transformacija § FFT postupci se općenito temelje na razlaganju n uzoraka niza u nekoliko grupa uzoraka. Pri tom se koristi periodičnost i simetrija eksponencijale § Pretpostavimo da sumaciju za dvije sume razložimo u G(n), H(n) - DFT od N/2 parnih i N/2 neparnih zoraka 32
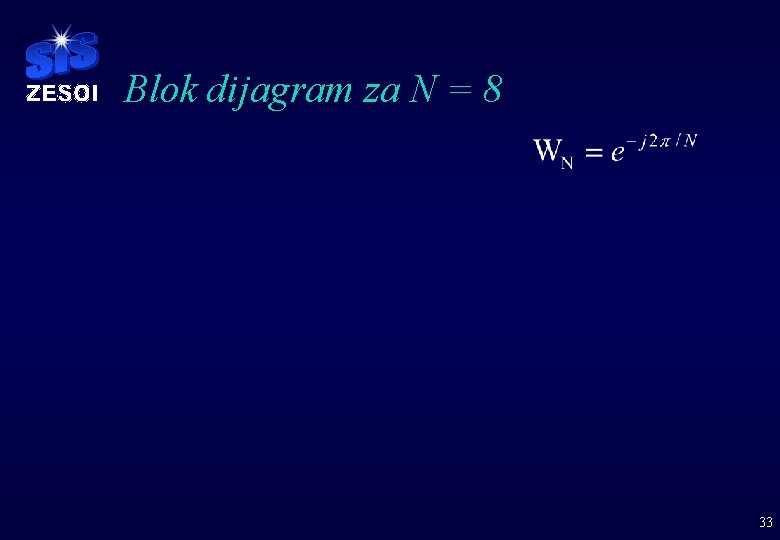
Blok dijagram za N = 8 33

§ § Brza Fourierova transformacija Dvije transformacije po N/2 uzoraka traži 2(N/2)2 N množenja s , n = 0, 1, . . . , N - 1, N zbrajanja. ® ušteda praktički N 2/2 Ako je N/2 i dalje paran broj možemo N/2 DFT odrediti s dvije DFT s N/4 uzoraka tj. 4(N/4)2 = N 2/4. 34

DFT leptir § U našem primjeru N = 8 svodi se na DFT od 2 uzorka. § Ova struktura se naziva DFT leptir. 35

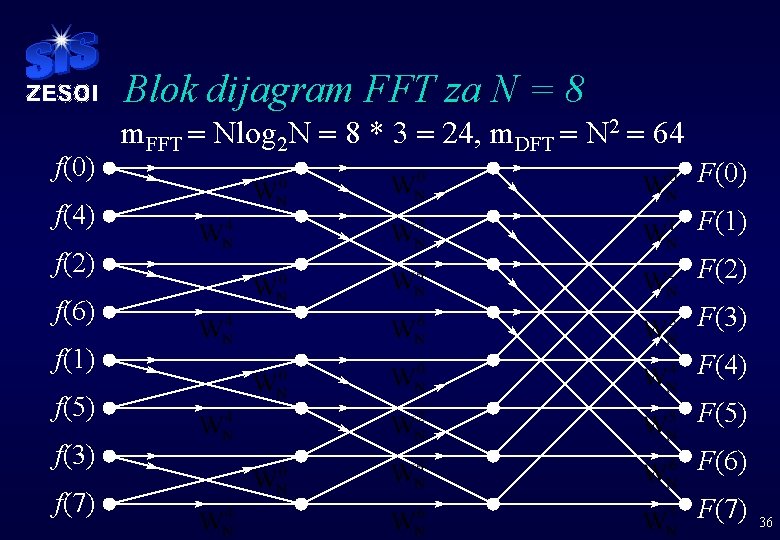
Blok dijagram FFT za N = 8 f(0) m. FFT = Nlog 2 N = 8 * 3 = 24, m. DFT = N 2 = 64 F(0) f(4) F(1) f(2) F(2) f(6) F(3) f(1) F(4) f(5) F(5) f(3) F(6) f(7) F(7) 36

Brza Fourierova transformacija q § U općem slučaju s N = 2 za svođenje na DFT od samo dva uzorka trebat će za postupak računanja q-stupnjeva. § Kako u svakom stupnju imamo N množenja izlazi m. FFT = Nlog 2 N 37

Brza Fourierova transformacija § Pokazali smo efikasan postupak za računanje DFT-a koristeći tzv. decimaciju u vremenskom domenu. § Na sličan način se može iskoristiti decimacija u frekvencijskom domenu. q § Kad je potrebna transformacija niza s N ¹ 2 , niz se može nadopuniti s nulama. 38

Literatura § R. A. Gabel & R. A. Roberts: “Signals and Linear Systems”, John Wiley & Sons, N. Y. Third Edition, 1987. § J. A. Cadzow: “Discrete Time Systems”, Prentice Hall, Inc. 1973. § Athans, Dertouzos, Spann & Mason: “Systems, Networks and Computation: Multivariable Methods”, Mc Graw - Hill, N. Y. , 1974. § E. I. Jury: “Theory and Applications of the Z Transform Method”, John Wiley & Sons, N. Y. , 1964. 39
 Branko jeren
Branko jeren Signali i sustavi
Signali i sustavi Fer signali i sustavi
Fer signali i sustavi Branko jeren
Branko jeren Branko jeren
Branko jeren Fer signali i sustavi
Fer signali i sustavi Branko jeren signali i sustavi
Branko jeren signali i sustavi Signali i sustavi branko jeren
Signali i sustavi branko jeren Signali i sustavi
Signali i sustavi Signali i sustavi
Signali i sustavi Signali i sustavi
Signali i sustavi Disjunkcija tablica
Disjunkcija tablica Metod diskusije po slovu
Metod diskusije po slovu Zoran mastilo
Zoran mastilo Vremenski stroj
Vremenski stroj Hromatska modulacija
Hromatska modulacija Koje opasnosti možete očekivati u situaciji kao na slici?
Koje opasnosti možete očekivati u situaciji kao na slici? Vesna radoman
Vesna radoman Digitalni signali
Digitalni signali Ekspertni sustavi
Ekspertni sustavi Raspodijeljeni sustavi
Raspodijeljeni sustavi Scada sustav
Scada sustav Poslovni informacijski sustavi
Poslovni informacijski sustavi Operacijski sustavi pmf
Operacijski sustavi pmf