Signali i sustavi AUDITORNE VJEBE 13 LSS FER

Signali i sustavi AUDITORNE VJEŽBE 13 LS&S FER - ZESOI

Primjena Z transformacije u rješavanju jednadžbi diferencija § Zadatak 1: Diskretni sustav je određen sljedećom jednadžbom diferencija: y(k + 2) – 3 y(k + 1) + 2 y(k) = 2 u(k + 1) – 2 u(k). § Naći odziv ovog sustava na pobudu:

Primjena Z transformacije § Da bi odredili odziv ovog sustava (bilo kojom metodom), potrebno je poznavati 2 početna uvjeta. § Budući pobuda počinje u koraku nula, od interesa nam je i odziv od toga koraka, pa je za njegovo izračunavanje potrebno poznavati početne uvjete u y(– 1) i y(– 2). § Pretpostavimo da su y(– 1) ¹ 0 i y(– 2) ¹ 0 § Nađimo odziv sustava u Z domeni.

Primjena Z transformacije § Koristeći izraz za Z–transformaciju niza pomaknutog u lijevo: § Transformiramo polaznu jednadžbu u:

Izračunavanje y(0) i y(1) iz početnih uvjeta § Pa je: § Očito je da sustav osim o pobudi ovisi i o y(0) i y(1). Ove vrijednosti su prva dva uzorka odziva i rezultat su doprinosa početnih stanja y(-2) i y(-1). § Za k = -2 polazna jednadžba prelazi u:

Izračunavanje y(0) i y(1) iz početnih uvjeta § Pa je: § Za k = -1 slijedi:

Primjena Z transformacije § Uvrstimo li y(0) i y(1) u izraz za Y(z) imamo: § Pa konačno pišemo:

Primjena Z transformacije, drugi pristup § Na trenutak ćemo prekinuti rješavanje da bismo prikazali drugi pristup. § Izvršimo pomak zadane jednadžbe u vremenskoj skali uvodeći supstituciju k' = k + 2. y(k') – 3 y(k'– 1) + 2 y(k'– 2) = 2 u(k'– 1) – 2 u(k'– 2). § Ovo je češći način pisanja jednadžbi diferencija (operator E-1 umjesto E !). § Ponovno ćemo odrediti Y(z) polazeći od ove nove jednadžbe. § Z–transformacija jednadžbe provodi se koristeći svojstvo:

Primjena Z transformacije, drugi pristup § Z–transformacija naše jednadžbe glasi:

Primjena Z transformacije § Dobili smo (naravno) isti izraz za Y(z) jer se radi o istom sustavu. § Sada ćemo nastaviti rješavanje našeg primjera uz pretpostavku da su početna stanja y(-1) = y(-2) = 0. § Uzimajući ovo u obzir Y(z) postaje:

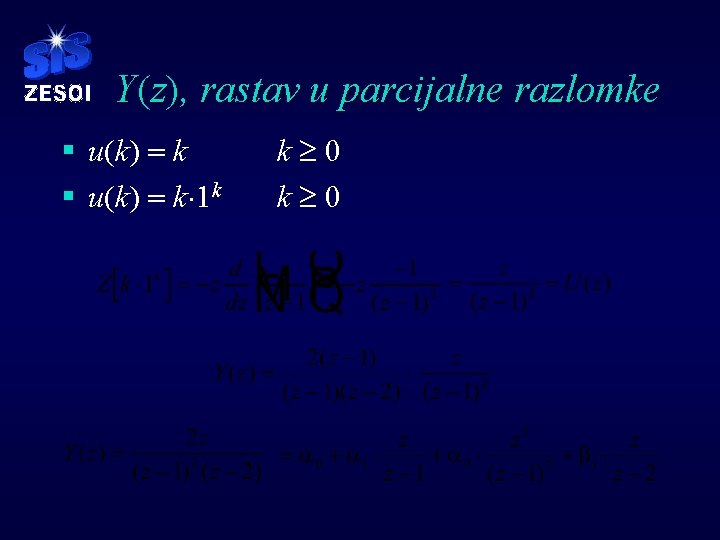
Y(z), rastav u parcijalne razlomke § u(k) = k× 1 k k³ 0

Tražimo koeficijente rastava. . . § a 0 = F(z)|z = 0 § a 1 određujemo iz Y(z) za npr. z = 3

Primjena Z transformacije, rješenje y (k )

Primjena Z transformacije Zadatak 2: § Diskretni sustav opisan je jednadžbom diferencija: § Odrediti odziv na pobudu:

Primjena Z transformacije, ulazni signal

Koeficijenti. . . rješavamo se j u nazivniku

Koeficijenti. . .

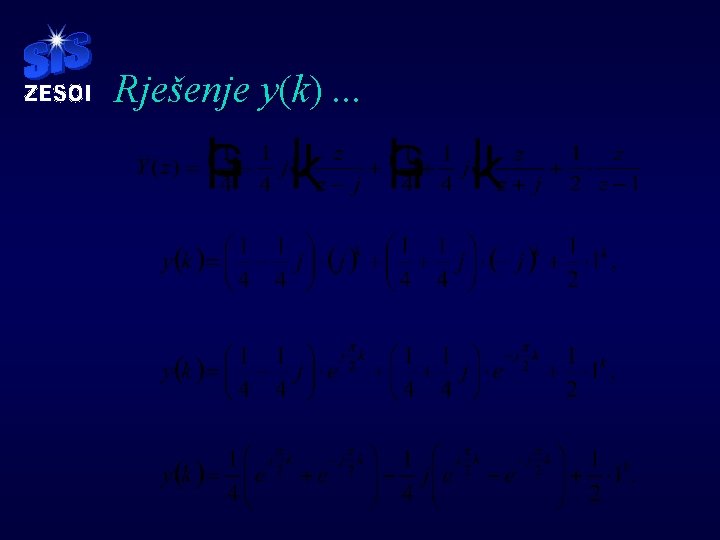
Rješenje y(k). . .

Konačno rješenje! § Ponovno dobivamo (iz prethodnih zadataka) već poznati odziv: y(k) 1 k

Primjena Z transformacije § Diskretni sustav opisan je sljedećim jednadžbama diferencija: a) Nacrtati model sustava koristeći zadane jednadžbe b) Izabrati varijable stanja i napisati jednadžbe stanja u matričnom obliku c) Nacrtati model sustava na temelju dobivenih jednadžbi stanja d) naći odziv sustava na pobudu

Primjena Z transformacije § Pobuda: e) Odrediti transfer matricu sustava, f) odrediti impulsni odziv sustava, g) transformirati sustav u kanonski oblik i nacrtati model, h) provjeriti osmotrivost i upravljivost.

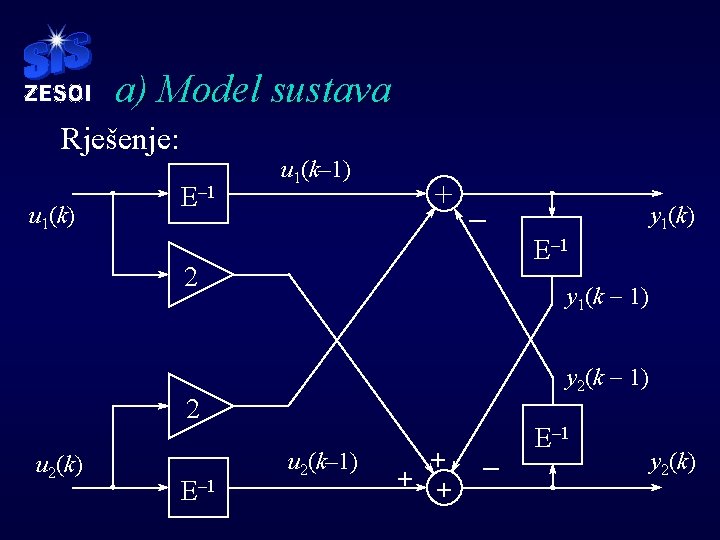
a) Model sustava Rješenje: u 1(k) E– 1 u 1(k– 1) + - 2 y 2(k - 1) u 2(k– 1) + + + E– 1 – E– 1 y 1(k - 1) 2 u 2(k) y 1(k) y 2(k)

b) Opis sustava varijablama stanja § Jednadžbe stanja kojima želimo opisati sustav trebaju biti oblika: § Očito je da pri izboru varijabli stanja u zadanim jednadžbama treba eliminirati u(k-1) i y(k-1):

b) Opis sustava varijablama stanja § Iz gornjih jednadžbi slijedi: (k ® k + 1) § Iz polaznih jednadžbi supstituiramo:

b) Opis sustava varijablama stanja § Iz ovoga slijedi: § Pa konačno pišemo jednadžbe stanja § Odnosno izlazne jednadžbe

b) Opis sustava varijablama stanja § U matričnom obliku pišemo:

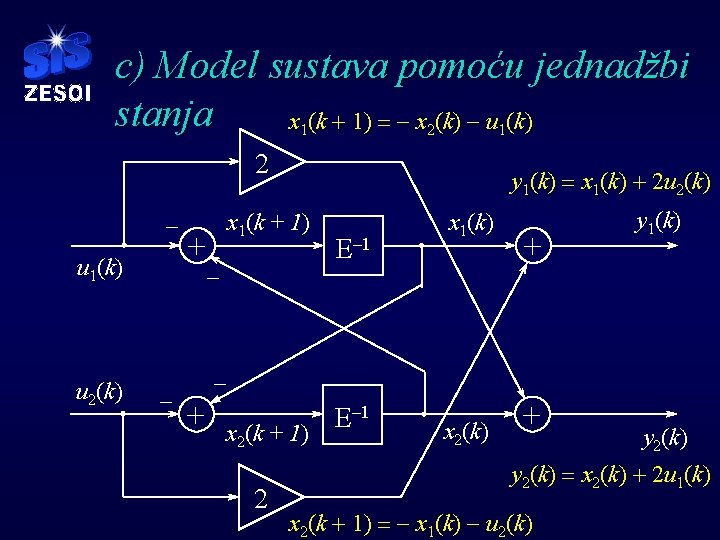
c) Model sustava pomoću jednadžbi stanja x (k + 1) = - x (k) - u (k) 1 2 u 1(k) x 1(k + 1) + E– 1 x 1(k) + y 1(k) - + - - u 2(k) y 1(k) = x 1(k) + 2 u 2(k) x 2(k + 1) 2 E– 1 x 2(k) + y 2(k) = x 2(k) + 2 u 1(k) x 2(k + 1) = - x 1(k) - u 2(k)

d) Odziv sustava na pobudu § Fundamentalnu matricu ćemo odrediti kao inverznu Z–transformaciju matrice karakterističnih frekvencija F(z). § Odredimo matrice z. I - A, det(z. I - A) i adj(z. I - A)

d) Odziv sustava na pobudu

d) Odziv sustava na pobudu § Da bi proveli inverznu Z–transformaciju F(z) treba njezine elemente rastaviti na parcijalne razlomke.

d) Odziv sustava na pobudu

d) Odziv sustava na pobudu § Pa je F(k):

d) Odziv sustava na pobudu § Odziv sustava odredit ćemo pomoću Z –transformacije

d) Odziv sustava na pobudu

d) Odziv sustava na pobudu § Sređivanjem dobijemo:

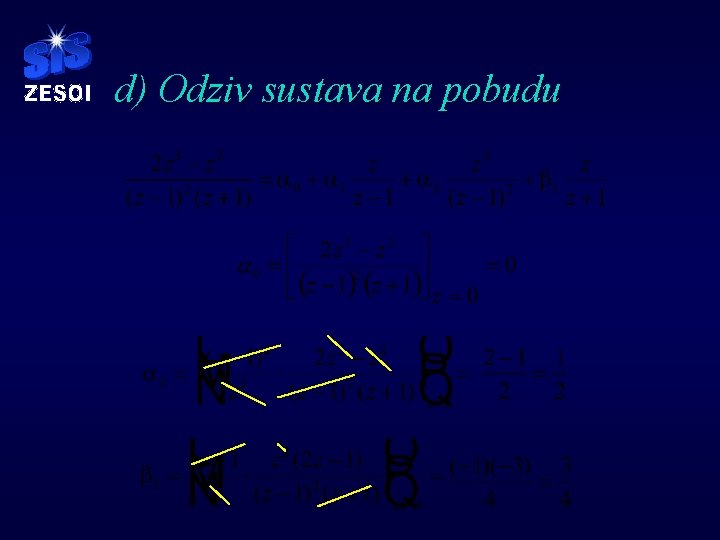
d) Odziv sustava na pobudu

d) Odziv sustava na pobudu § Za z = 2:

d) Odziv sustava na pobudu § Rastav na parcijalne razlomke:

d) Odziv sustava na pobudu § Za z = 2: § Pa je:

d) Odziv sustava na pobudu § Pa je odziv:

e) Transfer matrica sustava

f) Impulsni odziv sustava h(k) = Z– 1[H(z)]

f) Impulsni odziv sustava

f) Impulsni odziv sustava

g), h) Upravljivost, osmotrivost

g), h) Upravljivost, osmotrivost

g), h) Upravljivost, osmotrivost § Dakle, sustav je osmotriv i upravljiv

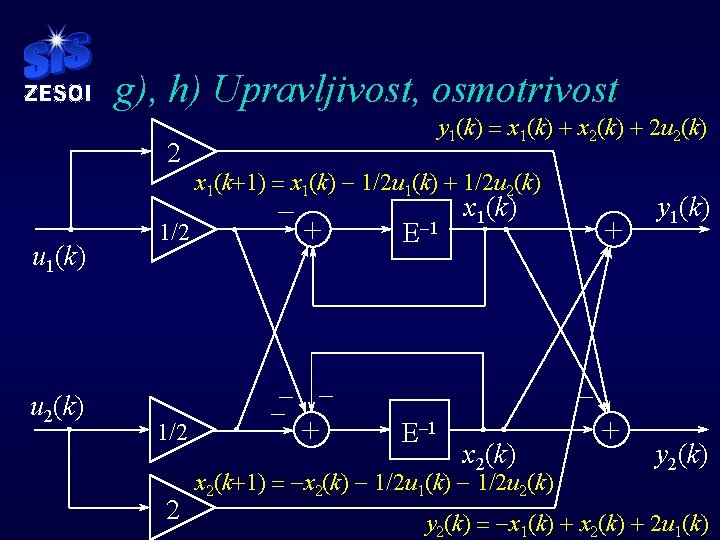
g), h) Upravljivost, osmotrivost u 1(k) u 2(k) 1/2 2 x 1(k+1) = x 1(k) - 1/2 u 1(k) + 1/2 u 2(k) – 2 y 1(k) = x 1(k) + x 2(k) + 2 u 2(k) + - - + E– 1 x 1(k) + y 1(k) E– 1 x 2(k) x 2(k+1) = -x 2(k) - 1/2 u 1(k) - 1/2 u 2(k) + y 2(k) = -x 1(k) + x 2(k) + 2 u 1(k)