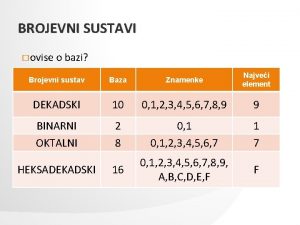
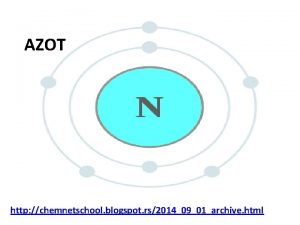
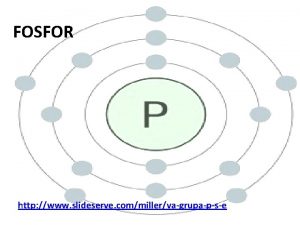
Signali i sustavi Odziv i svojstva linearnih sustava

Signali i sustavi Odziv i svojstva linearnih sustava

Sadržaj § Odziv nepobuđenog sustava. § Određivanje fundamentalne matrice razvojem u red. § Klasična metoda određivanja fundamentalne matrice. § Određivanje F(t) pomoću L - transformacije. § Odziv pobuđenog linearnog sustava. § Impulsni odziv sustava. § Odziv stanja sustava na eksponencijalnu pobudu. § Odziv sustava L - transformacijom. 2

Odziv nepobuđenog sustava § Dinamičko vladanje i svojstva linearnog sustava određujemo rješavanjem jednadžbi stanja sustava: § Rješenje matrične jednadžbe uz pobudu u i početno stanje x 0 = x(0) dati će nam stanje sustava od trenutka t 0 = 0 do bilo kojeg trenutka t. § Homogeni dio (bez pobude): uz rubni uvjet, odnosno uz početno stanje x 0 = x(0). 3

Odziv nepobuđenog sustava § Pretpostavimo x(t) oblika : § Uvrstimo u diferencijalnu jednadžbu stanja: § pa izjednačimo iste potencije od t: . . . ili općenito: 4

Odziv nepobuđenog sustava § Uvrštavanjem ck u izraz za x(t) dobivamo: § Razvoj sliči eksponencijalnoj funkciji, ali od matrice A! § Svojstva F(t): matrična eksponencijala F(t) 5

Odziv nepobuđenog sustava § Poznavanje F(t) i x 0 Þ omogućuje određivanje stanja sustava za bilo koji t > t 0. § F(t) - prijelazna ili fundamentalna matrica, transformira početno stanje x 0 u stanje x(t): § Deriviranje i integriranje F(t): 6

Određivanje fundamentalne matrice razvojem u red § Pogodno za numeričko određivanje fund. matrice. § Aproksimacija matrice e. At s N članova reda: § Izbor N: § Potreban N ovisit će o vlastitim vrijednostima matrice. 7

Određivanje fundamentalne matrice razvojem u red § Primjer matrične eksponencijale: 8

Određivanje fundamentalne matrice razvojem u red § Primjer matrične eksponencijale: 9

Određivanje fundamentalne matrice razvojem u red § Primjer matrične eksponencijale: 10

Određivanje fundamentalne matrice razvojem u red § Primjer matrične eksponencijale: 11

Određivanje fundamentalne matrice razvojem u red § Fiksiramo t = 1: § Numerički postupak: 12

Određivanje fundamentalne matrice razvojem u red . . . § Iterativni postupak određivanja: 13

Klasična metoda određivanja fund. matrice § Specijalni slučaj: matrica A dijagonalna, A = L Þ imamo n nezavisnih sustava prvog reda. § Rješenje za xi: § Svaka varijabla xi titra samo svojom frekvencijom: 17

Klasična metoda određivanja fund. matrice § Opća matrica A može se dijagonalizirati transformacijom varijabli stanja modalnom matricom M: L = M-1 A M i A = M L M-1. § Rješenje možemo iskoristiti za izračunavanje matrične eksponencijale od A: e. At = M e. Lt M-1, § te slijedi odziv stanja: x(t) = M e. Lt M-1 x 0. 18

Geometrijska interpretacija rješenja § Neka je matrica A: § Pripadne svojstvene vrijednosti i karak. vektori su: § Kako će se mijenjati stanje x(t), ako je početno stanje x(0) proporcionalno nekom od 19 karakterističnih vektora?

Geometrijska interpretacija rješenja MATLAB primjer 20

Određivanje F(t) pomoću L - transformacije § Vektor stanja sustava x(t) transformira se kao: L {x(t)} = X(s) i obratno L-1{X(s)} = x(t). § Jednadžba stanja sustava u s domeni: § X(s) stupčasti vektor [X 1(s) X 2(s). . . Xn(s)]T § Riješimo po X(s): Matrica karakterističnih frekvencija ili resolventa sustava. 21

§ Određivanje F(t) pomoću L - transformacije F(t): . . . L transf. fundamentalne matrice sustava § Elementi matrice - razlomljene racionalne funkcije kompleksne frekvencije s. § Brojnik - polinom n - 1 stupnja. § Nazivnik - polinom n-tog stupnja. 22

Određivanje F(t) pomoću L - transformacije § Determinanta det(s. I - A) kao produkt korjenih faktora: § p 1 do pn. . karakteristične frekvencije sustava. § mi. . višestrukost i-tog korijena 23

Određivanje F(t) pomoću L - transformacije § Determinanta det(s. I - A) kao polinom: det(s. I - A) = sn + d 1 sn - 1 +. . . + dn - 1 s + dn § koeficijenti polinoma {di} mogu se dobiti iz tragova matrice A i njenih potencija: § iterativni postupak 24

Određivanje F(t) pomoću L - transformacije § Inverzna L transformacija od (s. I - A)-1. § Razvojem u parc. razlomke svakog elementa jjk(s) 25

Određivanje F(t) pomoću L - transformacije § U slučaju jednostrukog korijena: § Inverzna transformacija daje fundamentalnu matricu oblika: § Suma eksponencijala eventualno pomnoženih polinomom u varijabli t, (mk - 1) stupnja, ako je frekvencija (pk) višestruki korijen. 26

Odziv pobuđenog linearnog sustava § Za totalni odziv sustava treba odrediti rješenje nehomogene matrične jednadžbe § Lagrange-ova metoda varijacije parametara § proizvoljne konstante rješenja homogene jednadžbe pretpostave se kao funkcija vremena: x(t) = e. At f(t). § Uvrštenjem u jednadžbu sustava slijedi: odnosno: 27

Odziv pobuđenog linearnog sustava § Integriranjem u intervalu (0, t] slijedi: x(t) = e. Atf(t) § Za t = 0 slijedi: x(0) = f(0), pa se stanje sustava može naći kao: 28

Odziv pobuđenog linearnog sustava § Budući da je F(t) = e. At, stanje sustava se može zapisati i kao: Titranje početnog stanja, ili funkcija stanja sustava xn(t) kad nema pobude. Stanje uzrokovano pobudom, ili odziv stanja mirnog sustava xm(t). 29

Odziv pobuđenog linearnog sustava § Uvrstimo stanje x(t) u izlaznu jednadžbu sustava: odziv sustava bez pobude odziv mirnog sustava ili, općenito za pobudu koja počinje u trenutku t 0: 30

Odziv pobuđenog linearnog sustava § Konvolucijski integral daje cjelovit odziv i kada t 0 teži prema -¥, ako je pobuda trajna (-¥, ¥): § Početno stanje x(-¥) je proizvoljno - vlastito titranje uslijed početnog uvjeta ne postoji niti u jednom (konačnom) trenutku t. 31

Impulsni odziv sustava § Pobuda sustava impulsima u(t) = Ud (t). § Elementi stupca U su intenziteti impulsa na pojedinim ulazima sustava. § Stanje sustava: § Stanje sustava bez pobude određeno stanjem x(0 -). § Stanje mirnog sustava određeno impulsima pobude BU. 32

Impulsni odziv sustava § Pobuda razložena na impulse: § Množenjem matricom D i uvrštavanjem u konvolucijski integral dobivamo odziv mirnog sustava: matrica impulsnog odziva 33

Impulsni odziv sustava § Konvolucijski integral predstavlja cjelovit odziv kauzalnog sustava kada t 0 teži u -¥: § U slučaju nekauzalnog sustava gornja granica integracije se proteže u +¥: 34

Odziv stanja sustava na kauzalnu eksponencijalnu pobudu § Pobuda sustava: § Elementi stupca U (U 1 do Um) su amplitude stepenice na pojedinim ulazima sustava. § Stanje sustava: 35

Odziv stanja sustava na kauzalnu eksponencijalnu pobudu § U izrazu prepoznajemo tri komponente: xn(t), stanje nepobuđenog sustava koje titra vlastitim frekv. sustava xms(t), stanje mirnog sustava koje titra frekvencijom pobude s 0 xmp(t), stanje mirnog sustava koje titra vlastitim frekv. sustava 36

Odziv stanja sustava na kauzalnu eksponencijalnu pobudu § Spajamo članove koji titraju istim frekvencijama: Prijelazno stanje sustava Stacionarno stanje sustava § Desni pribrojnik se naziva i stacionarnim stanjem u slučaju konstantne s 0 = 0 ili periodičke s 0 = jw 0 pobude. § Amplitude titranja prijelaznog stanja određene su neskladom između početnog stanja x(0) i stacionarnog stanja xms(0) u trenutku t = 0. 37

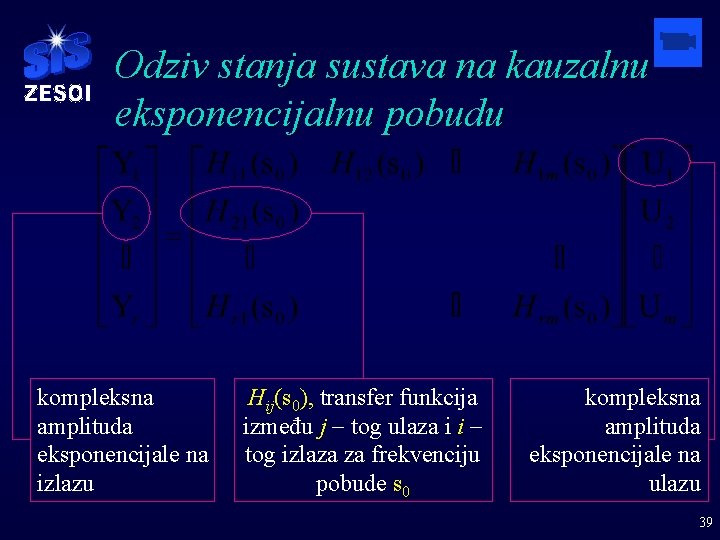
Odziv stanja sustava na kauzalnu eksponencijalnu pobudu § Odziv stanja sustava se može pisati i kao: § Cjelovit odziv sustava na eksponencijalnu pobudu: Stacionarni odziv sustava, ys(t) Prolazni ili prijelazni odziv sustava, ypr(t) § Partikularno rješenje ili stacionarni odziv: transfer matrica 38

Odziv stanja sustava na kauzalnu eksponencijalnu pobudu kompleksna amplituda eksponencijale na izlazu Hij(s 0), transfer funkcija između j - tog ulaza i i tog izlaza za frekvenciju pobude s 0 kompleksna amplituda eksponencijale na ulazu 39

Odziv stanja sustava na kauzalnu eksponencijalnu pobudu § Odziv sustava na harmonijsku pobudu, s 0 = jw: u(t) = Uejwtm(t), x(t) = e. At[x(0) - (jw. I - A)-1 BU] + (jw. I - A)-1 BUejwt, y(t) = CF(t)[x(0) - (jw. I - A)-1 BU] + [C(jw. I - A)-1 B + D] Uejwt. § Stacionarni odziv: transfer matrica pri frekvenciji w § Veza transfer matrice impulsnog odziva: 40

Odziv sustava L - transformacijom § L transformacija jednadžbi stanja sustava: s. X(s) - x(0) = AX(s) + BU(s), (s. I - A)X(s) = x(0) + BU(s), X(s) = (s. I - A)-1 x(0) + (s. I - A)-1 BU(s), fundamentalna matrica F(t) = e. At 41

Odziv sustava L - transformacijom § L transformacija izlazne jednadžbe sustava: Y(s) = CX(s) + DU(s), § Miran sustav: x(0) = 0: transfer matrica § Elementi matrice su transfer funkcije između pojedinih ulaza i pojedinih izlaza sustava. 42

Odziv sustava L - transformacijom § Inverznom L transformacijom transfer matrice dobiva se matrica impulsnog odziva H(t): 43