Sustavi s pravilima Ekspertni sustavi zasnovani na pravilima

Sustavi s pravilima Ekspertni sustavi zasnovani na pravilima (prirodno zaključivanje) 1

Sustavi s pravilima Zašto sustavi s pravilima ? Implikacija u predikatnoj logici: (2 (2 + + 2 2 = = 4) 4) 5) 5) (“Zagreb je glavni grad Hrvatske”) (“London je glavni grad Hrvatske”) istinito neistinito To je materijalna implikacija i nije potpuno intuitivna prirodnom jeziku. Namjera materijalne implikacije je modelirati uvjetnu konstrukciju, (a ne uzročno-posljedičnu vezu), t. j. : (P Q) ima slijedeću semantiku: Ako je P istinit, tada je (P Q) istinito samo ako je Q istinito. Ako je P neistinit, tada je (P Q) istinito bez obzira na Q. 2

Sustavi s pravilima n n n Shema predstavljanja znanja temeljena na pravilima predstavljena je 1970. god. (Newell i Simon). Reaktivni agent s memorijom sadrži skup pravila (znanje o domeni) i skup činjenica (sliku svijeta). Vidi: racionalni agent s memorijom. Pravila imaju dva dijela: lijevi dio (uzrok, pretpostavka, uvjet) – AKO (engl. IF). desni dio (zaključak, akcija, odziv) - TADA (engl. THEN). AKO: (svjetla ne rade) i AKO: (elektro-pokretač ne vrti motor) TADA: (akumulator je ispražnjen) Simbolički prikaz pravila (nije standardizirano ovisi o implementaciji): ((P() Q()) R()) P, Q, R su najčešće reducirani (ograničeni) logički predikati (varijable su nužne). Jedna moguća implementacija pravila u LISP kodu (15 može biti redni broj pravila ili težinski koeficijent): (rule 15 if (prizma (var x)) then (geom_tijelo (var x))) 3

Sustavi s pravilima n n n n n Činjenice predstavljaju sliku svijeta. Simbolički prikaz: P(a), Q(b), R(c) Jedna moguća implementacija pravila u LISP kodu: (prizma tijelo_112) Zaključivanje s pravilima Traži se slaganje (poklapanje) činjenica (slike svijeta) s AKO stranama u pravilima (znanjem o domeni). (engl. pattern matching, data driven). Pravila koja postignu slaganje se izvode (neproceduralan tijek). Poteškoće u postupku zaključivanja: Činjenice mogu biti složene strukture podataka (usporava poklapanje). Mnogo pravila može postupak pretraživanja i poklapanja s činjenicama učiniti neprihvatljivim (potrebna je optimizacija pretraživanja). Konjunkcija u AKO stranama pravila (produljeno vrijeme poklapanja). Slaganje činjenica s više pravila (mogućnost konflikta). Povezani ciklusi zaključivanja (mogućnost ulaska u beskonačnu petlju). 4

Sustavi s pravilima – dva postupka zaključivanja Zaključivanje ulančavanjem unatrag (engl. backward chaining, query time inferencing, goal driven) Neka postoji činjenica P(a) i pravilo: (P(X) Q(X)). X je varijabla. P(a) (P(X) Q(X)) Korisnik postavlja upit ili cilj koji se pretražuje u činjenicama, pa ako se ne nalazi nastoji se potražiti u TADA stranama čija se potvrda (novi cilj) traži u AKO stranama istih pravila i u činjenicama: Primjeri (za gornji slučaj): ? P(a) - ovdje odmah odgovor DA. ? R(b) - nema u činjenicama, a također je i TADA strana pravila različita, odgovor je NE. ? Q(a) - nema u činjenicama, ali se odgovarajućom supstitucijom varijabli (X = a) može pronaći u TADA strani pravila. n Supstitucija se mora provesti u cijelom pravilu. Novo stanje sustava je: P(a) (P(a) Q(a)) 5

Sustavi s pravilima – dva postupka zaključivanja Zaključivanje ulančavanjem unatrag n n Potvrda za Q(a) se treba potražiti u AKO strani, t, j, novi cilj je P(a) se nalazi u činjenicama. Time je istinitost Q(a) potvrđena te se ta nova činjenica najčešće dodaje u skup činjenica kako bi u mogućem budućem upitu odgovor bio brži. Novo stanje sustava je: Q(a) P(a) (P(a) Q(a)) n Konačno, varijable u pravilima se oslobađaju i sustav je spreman za novi ciklus: Q(a) P(a) (P(X) Q(X)) n n Zaključak je uvijek unija odgovora i provedene supstitucije. Ciljevi i podciljevi mogu biti višestruki povezani konjunkcijom. 6

Sustavi s pravilima – dva postupka zaključivanja Zaključivanje ulančavanjem unaprijed (engl. forward chaining, assertion time inference, implication driven, data driven) Neka u sustavu postoji pravilo (P(X) Q(X)) U sustav se zatim, kao rezultat nekog događaja, upiše činjenica P(a), te je stanje : P(a) (P(X) Q(X)) n n U trenutku upisa P(a) u sustav, započinje automatska (samostalna) potraga za pravilom koje u svom AKO dijelu ima strukturu koja bi se mogla izjednačiti s P(a). Supstitucijom X=a to se nalazi, pa je stanje: P(a) (P(a) Q(a)) n U pravilu je zadovoljen uvjet (AKO), te se posljedica izvođenja pravila upisuje u sustav kao nova činjenica Q(a). Sada je stanje: Q(a) P(a) (P(a) Q(a)) 7

Sustavi s pravilima – dva postupka zaključivanja Zaključivanje ulančavanjem unaprijed Konačno, varijable se oslobađaju, te je sustav spreman za novi ciklus u stanju: Q(a) P(a) (P(X) Q(X)) 8

Sustavi s pravilima – dva postupka zaključivanja Ulančavanje unaprijed i konjunkcije u pravilima Neka je u sustav upisano pravilo: ((P(X) Q(X)) R(X)) n n n Upisom P(a) započinje pretraživanje slaganja. P(a) je moguće izjednačiti s P(X), ali treba zadovoljiti i Q(X) (konjunkcija u AKO strani pravila). Ostaje upisano samo P(a). Eventualnim upisom dodatne činjenice Q(a) stanje činjenica se uspoređuje sa pravilima (AKO stranama) i istovremeno se izjednači P(X) s P(a), te Q(X) s Q(a). Stanje je: P(a) Q(a) ((P(a) Q(a)) R(a)) Nakon supstitucije X=a, zaključuje se R(a) i dodaje u skup činjenica. Nakon toga povezivanje varijabli u pravilima se oslobađa. Stanje je: R(a) P(a) Q(a) ((P(X) Q(X)) R(X)) 9

Sustavi s pravilima – dva postupka zaključivanja Ulančavanje unaprijed i višestruka pravila Neka se u sustav zapišu činjenice: C 1, C 3, C 5, a pravila su: 1. ((C 1 C 2) A 1) 2. (C 3 A 2) 3. ((C 1 C 3) A 3) 4. (C 4 A 4) 5. (C 5 A 5) n Stanje činjenica zadovoljava pravila: 2, 3, 5. n Sva ta pravila čine tzv. konfliktni skup (u sustavu CLIPS – agenda). n Potrebno je izabrati jedno i samo jedno koje će generirati neku akciju. n Mogući postupci izbora: prvo iz konfliktnog skupa, slučajno, težine, …. U općem slučaju faze ciklusa zaključivanja ulančavanjem unaprijed su: usporedi (engl. match) AKO strane pravila s činjenicama, razriješi (engl. resolve) konfliktni skup i djeluj (engl. act), t. j. aktiviraj odabrano pravilo. 10

Sustavi s pravilima – dva postupka zaključivanja Ulančavanje unaprijed i vezani ciklusi Neka su u sustavu zapisana pravila: 1. ((B D E) F) 2. ((D G) A) 3. ((C F) A) 4. (C D) 5. (D E) 6. (A H) Upisom činjenice B u skup činjenica, neće se zadovoljiti niti jedno pravilo. Dodatnim upisom npr. C, odvija se akcija u više ciklusa: n C aktivira pravilo 4, D se upisuje u skup činjenica. n D aktivira pravilo 5. n B, D, E, pravilo 1; C, F, pravilo 3; A, pravilo 6 koje upisuje H. n U skupu činjenica ostaju: A, B, C, D, E, F, H (sve osim G). Vezani ciklusi mogu generirati beskonačnu petlju, te sustav s pravilima mora imati mehanizam izlaska iz beskonačnih petlji. Pravilom upisana činjenica može bit u kontradikciji s ranije upisanim činjenicama- Sustav mora imati mehanizam održavanja konzistentnosti –TMS (engl. Truth Maintenance System). 11

Sustavi s pravilima – dva postupka zaključivanja RETE algoritam n Uočeno je da tijekom izvođenja zaključivanja ulančavanjem unaprijed, sustav najveći dio vremena provodi u usporedbi lijevih strana pravila sa sadržajem radne memorije. n RETE algoritam reducira ukupno vrijeme usporedbe koristeći dijelom već izvršenu usporedbu u ranijim ciklusima, kao i činjenicu da u skupu pravila postoje neki identični dijelovi lijevih strana. n Pri upisu pravila (prije činjenica i zaključivanja), algoritam gradi mrežu tzv. uvjetovanih zavisnosti, koja povezuje sva pravila s jednakim dijelovima AKO (lijeve) strane. n U radu, sustav, umjesto da pretražuje iscrpno i linearno, prolazi mrežom uvjetovanih zavisnosti. n Izlazni podaci po prolazu kroz mrežu predstavljaju parove elemenata: oznaku pravila i listu činjenica iz radne memorije koje odgovaraju lijevoj strani pravila. n RETE mreža, kao usmjereni aciklički graf, omogućuje izravno preslikavanje u podatkovno vođeni model programa. 12

Sustavi s pravilima – dva postupka zaključivanja Izbor postupka zaključivanja (ulančavanja) 1. Analiziraju se AKO i TADA strane pravila. n Ukoliko postoji mnogo uvjeta (više nego zaključaka) u "tipičnom pravilu“, to ukazuje na potrebu ulančavanja unaprijed. n Ulančavanje unatrag generiralo bi mnogo novih upita. n Ukoliko postoji malo uvjeta: ulančavanje unatrag. 2. Ako nije moguće zaključiti dominantnost u pravilima – potrebna je analiza skupa činjenica n Ako su sve činjenice poznate, a potrebno je vidjeti kamo to vodi, koristi se ulančavanje unaprijed. n Ako je pak malo činjenica poznato, a cilj je potvrditi jednu od mnogih hipoteza, koristi se ulančavanje unatrag. 13

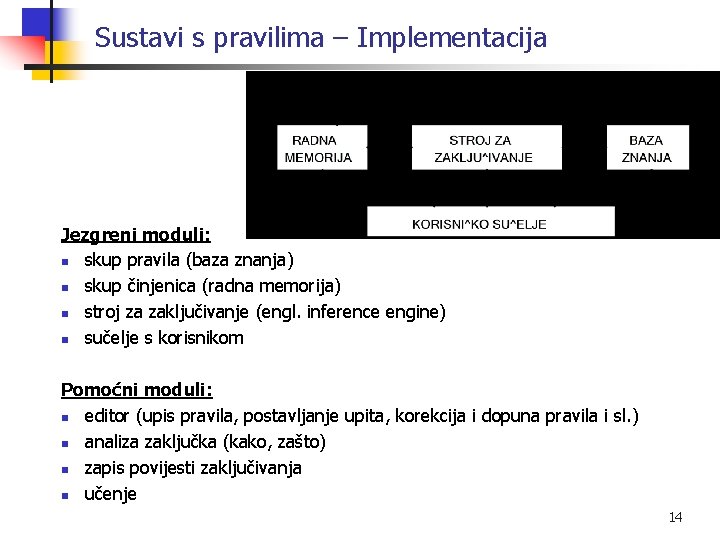
Sustavi s pravilima – Implementacija Jezgreni moduli: n skup pravila (baza znanja) n skup činjenica (radna memorija) n stroj za zaključivanje (engl. inference engine) n sučelje s korisnikom Pomoćni moduli: n editor (upis pravila, postavljanje upita, korekcija i dopuna pravila i sl. ) n analiza zaključka (kako, zašto) n zapis povijesti zaključivanja n učenje 14

Sustavi s pravilima – neki izvedeni sustavi Sustav s pravilima bez upisanih činjenica i pravila naziva se ljuska ekspertnog sustava. Komercijalne ljuske: n G 2, Unix, real-time, Gensym Corp. (MIT). n KEE (Knowledge engineering environment), Unix, Intelli. Corp, n NEXPERT, Windows, Unix, C, Neuron Data, Palo Alto. n OPS 83, nasljednik OPS 5, Unix, CMU (RETE, ulančavanje unaprijed, unatrag i kombinacija oba postupka. n Personal Consultant Plus, Texas Instruments, LISP. Slobodne ljuske: n CLIPS - Windows, poput OPS-a, NASA, C, OO dio. n FOCL - Unix, učenje, LISP, UC Irwine, CA. n OPS 5, Unix, CMU, predak OPS 83. n MIKE, DOS, Open Univ. , V. Brit. , PROLOG, RETE algoritam. 15

Sustavi s pravilima – Zaključci (1/2) Prednosti: n n n n Izravni prirodni prikaz i korištenje empiričkog znanja prikupljenog od eksperata određene (uske) domene. Modularnost zbirke znanja i njeno jednostavno održavanje. Efikasno izvođenje u uskim domenama. Dobra obilježja razjašnjavanja procesa automatiziranog rasuđivanja (kako, zašto). Skup pravila prirodno se preslikava u problem pretraživanja prostora stanja. Koraci tijekom rješavanja problema su transparentni. Olakšava izradu sučelja temeljenih na dijalogu s korisnikom. Razdvajanje upravljačkog toka i zbirke znanja olakšava projektiranje i izradu inteligentnih sustava (deklarativno, iterativno i inkrementalno). 16

Sustavi s pravilima – Zaključci (2/2) Nedostaci: n n n Pravila prikupljena od eksperata su heuristička i fragmentarna (“grumeni znanja”) i ne objašnjavaju cjelovite odnose u procesu. Ponekad mogu bit i konfliktna (potrebno održavanje konzistencije). Pravila u klasičnom sustavu nisu robusna, te ne uključuju neizvjesno i nepotpuno znanje (noviji sustavi poput Fuzzy. CLIPS posjeduju predstavljanje i zaključivanje s neizvjesnim znanjem). Sustav s pravilima naglo prestaje biti uporabiv na rubu domene, umjesto da poput eksperata monotono slabi u rješavanju problema. Razjašnjenja, koja slijede iz prikaza ulančavanja, ne daju kauzalne veze u procesu (nema povezivanja dubinskih uzroka i posljedica). Znanje prikazano pravilima prilagođeno je određenom zadatku, s malom fleksibilnošću i širinom – pretpostavka zatvorenog svijeta (što je vrlo različito prema znanju eksperata). U razvoju sustava postoji poteškoća razumijevanja između inženjera znanja i eksperta domene. 17