Shodnost trojhelnk stedov soumrnost opakovn Matematika 8 ronk

Shodnost trojúhelníků, středová souměrnost opakování Matematika – 8. ročník

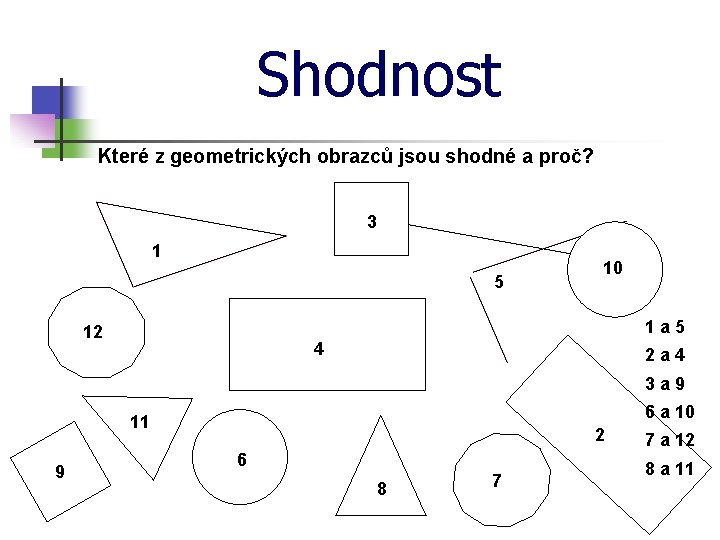
Shodnost Které z geometrických obrazců jsou shodné a proč? 3 1 5 10 1 a 5 12 4 2 a 4 3 a 9 6 a 10 11 9 2 6 8 7 7 a 12 8 a 11

Shodnost Dva geometrické útvary v rovině nazýváme shodné, právě když je lze přemístit (položit na sebe) tak, že se navzájem kryjí. Pokud jsou geometrické útvary shodné, mohou být shodné přímo nebo nepřímo. Přímo shodné útvary jsou ty, které lze navzájem překrýt pouze posouváním či otáčením útvarů. Nepřímo shodné útvary jsou ty, které lze navzájem překrýt pouze s pomocí převrácení jednoho z útvarů (zrcadlové).

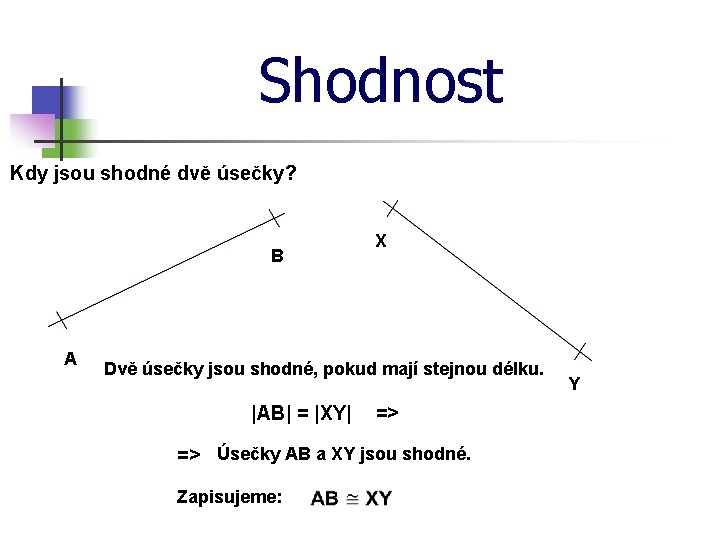
Shodnost Kdy jsou shodné dvě úsečky? B A X Dvě úsečky jsou shodné, pokud mají stejnou délku. |AB| = |XY| => => Úsečky AB a XY jsou shodné. Zapisujeme: Y

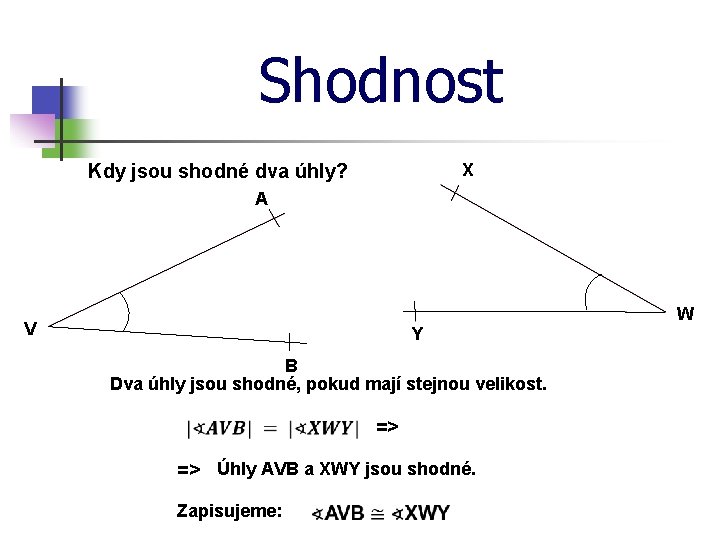
Shodnost X Kdy jsou shodné dva úhly? A W V Y B Dva úhly jsou shodné, pokud mají stejnou velikost. => => Úhly AVB a XWY jsou shodné. Zapisujeme:

Shodnost Odpovězte na otázky ANO nebo NE: Všechny přímky jsou shodné. ANO Všechny čtverce jsou shodné. NE Všechny pravé úhly jsou shodné. ANO Všechny kružnice se stejným poloměrem jsou shodné. ANO Všechny tupé úhly jsou shodné. NE Všechny polopřímky jsou shodné. ANO Všechny úsečky jsou shodné. NE Všechny rovnostranné trojúhelníky jsou shodné. NE

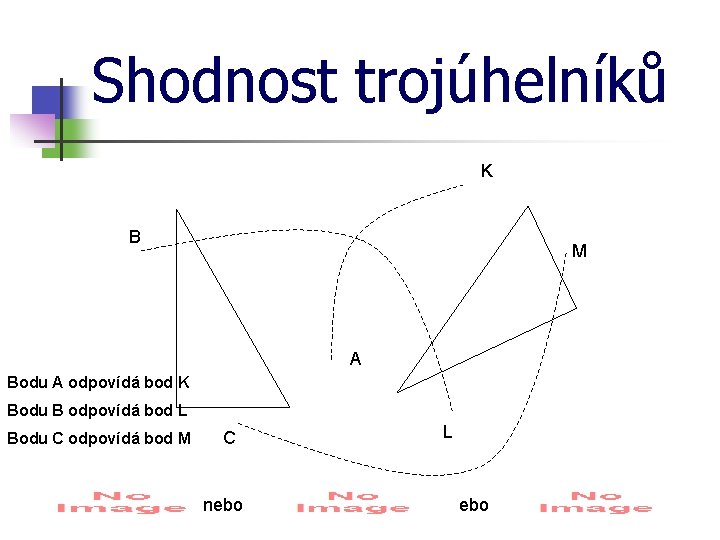
Shodnost trojúhelníků K B M A Bodu A odpovídá bod K Bodu B odpovídá bod L Bodu C odpovídá bod M C nebo L nebo

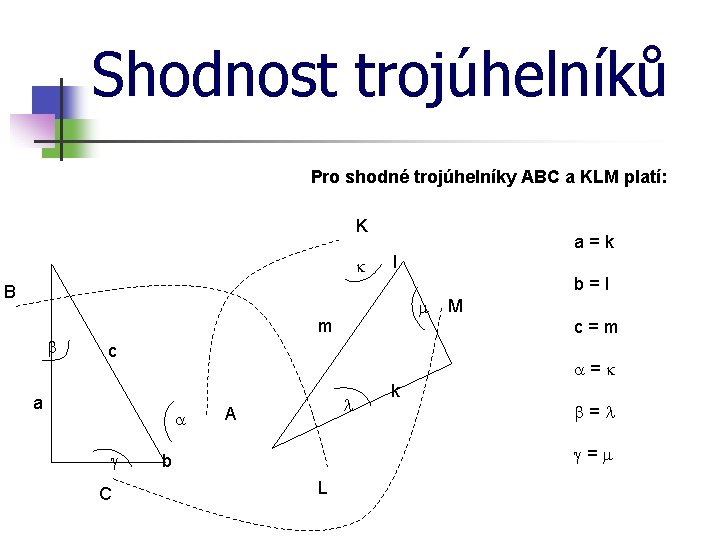
Shodnost trojúhelníků Pro shodné trojúhelníky ABC a KLM platí: K k l b=l B b m m c C M c=m =k a g a=k l A k b=l g=m b L

Shodnost trojúhelníků

Konstrukce trojúhelníků Postup při konstrukcích trojúhelníků: 1) Pozorně si přečteme a analyzujeme zadání úlohy. 2) Náčrt a Rozbor úlohy, kde si načrtneme a zakreslujeme postup budoucí konstrukce. 3) Postup konstrukce je přesný postup zapsaný pomocí matematických značek - symbolů, písmen a čísel. 4) Konstrukce – samotné (přesné) narýsování trojúhelníku. 5) Důkaz – ověření, zda sestrojený trojúhelník odpovídá zadání. 6) Diskuze – zjištění možného počtu řešení za daných podmínek (využití především od 8. ročníku)

Konstrukce trojúhelníků Věta sss Sestrojte trojúhelník ABC je-li: a = 45 mm; b = 72 mm a c = 56 mm. 1) Pozorně si přečteme a analyzujeme zadání úlohy. Abychom trojúhelník mohli sestrojit musí platit trojúhelníková nerovnost (trojúhelníkové nerovnosti). a+c>b 45 + 56 > 72 101 > 72

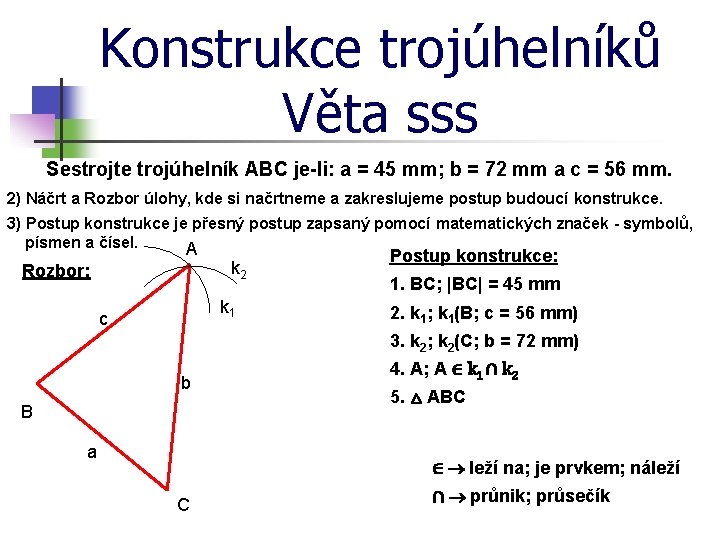
Konstrukce trojúhelníků Věta sss Sestrojte trojúhelník ABC je-li: a = 45 mm; b = 72 mm a c = 56 mm. 2) Náčrt a Rozbor úlohy, kde si načrtneme a zakreslujeme postup budoucí konstrukce. 3) Postup konstrukce je přesný postup zapsaný pomocí matematických značek - symbolů, písmen a čísel. A k 2 Rozbor: k 1 c Postup konstrukce: 1. BC; |BC| = 45 mm 2. k 1; k 1(B; c = 56 mm) 3. k 2; k 2(C; b = 72 mm) b B a 4. A; A ∈ k 1 ∩ k 2 5. △ ABC ∈ leží na; je prvkem; náleží C ∩ průnik; průsečík

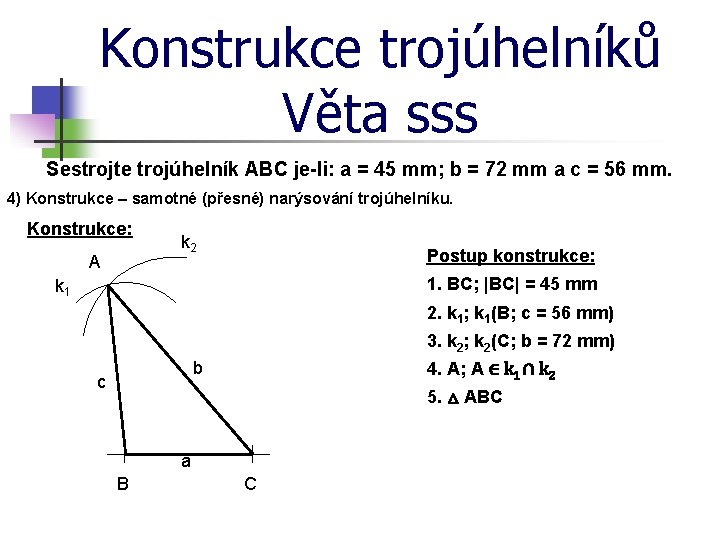
Konstrukce trojúhelníků Věta sss Sestrojte trojúhelník ABC je-li: a = 45 mm; b = 72 mm a c = 56 mm. 4) Konstrukce – samotné (přesné) narýsování trojúhelníku. Konstrukce: A k 2 Postup konstrukce: 1. BC; |BC| = 45 mm k 1 2. k 1; k 1(B; c = 56 mm) 3. k 2; k 2(C; b = 72 mm) b c 4. A; A ∈ k 1 ∩ k 2 5. △ ABC a B C

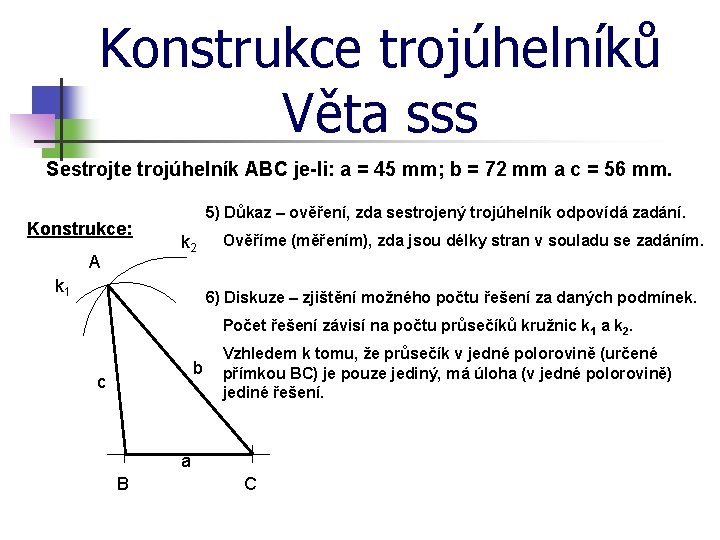
Konstrukce trojúhelníků Věta sss Sestrojte trojúhelník ABC je-li: a = 45 mm; b = 72 mm a c = 56 mm. Konstrukce: A 5) Důkaz – ověření, zda sestrojený trojúhelník odpovídá zadání. k 2 k 1 Ověříme (měřením), zda jsou délky stran v souladu se zadáním. 6) Diskuze – zjištění možného počtu řešení za daných podmínek. Počet řešení závisí na počtu průsečíků kružnic k 1 a k 2. b c Vzhledem k tomu, že průsečík v jedné polorovině (určené přímkou BC) je pouze jediný, má úloha (v jedné polorovině) jediné řešení. a B C

Konstrukce trojúhelníků Věta sus Sestrojte trojúhelník ABC je-li: a = 53 mm; b = 69 mm a = 56°. 1) Pozorně si přečteme a analyzujeme zadání úlohy. Abychom trojúhelník mohli sestrojit musí být velikost zadaného úhlu menší než 180°. < 180° 56° < 180°

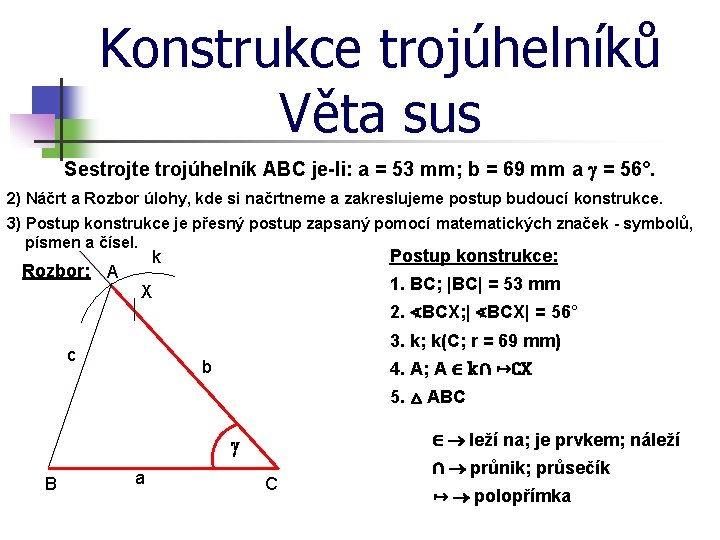
Konstrukce trojúhelníků Věta sus Sestrojte trojúhelník ABC je-li: a = 53 mm; b = 69 mm a = 56°. 2) Náčrt a Rozbor úlohy, kde si načrtneme a zakreslujeme postup budoucí konstrukce. 3) Postup konstrukce je přesný postup zapsaný pomocí matematických značek - symbolů, písmen a čísel. Postup konstrukce: k Rozbor: A 1. BC; |BC| = 53 mm X 2. ∢BCX; | ∢BCX| = 56° 3. k; k(C; r = 69 mm) c b 4. A; A ∈ k ∩ ↦CX 5. △ ABC ∈ leží na; je prvkem; náleží B a C ∩ průnik; průsečík ↦ polopřímka

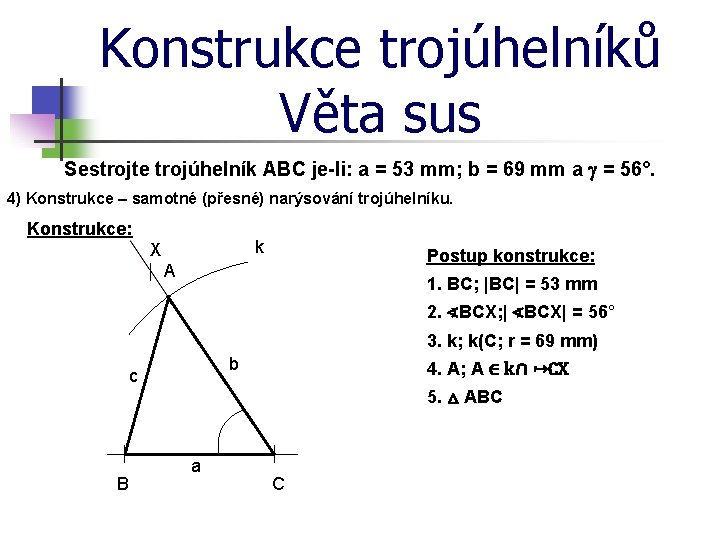
Konstrukce trojúhelníků Věta sus Sestrojte trojúhelník ABC je-li: a = 53 mm; b = 69 mm a = 56°. 4) Konstrukce – samotné (přesné) narýsování trojúhelníku. Konstrukce: k X Postup konstrukce: A 1. BC; |BC| = 53 mm 2. ∢BCX; | ∢BCX| = 56° 3. k; k(C; r = 69 mm) b c 4. A; A ∈ k ∩ ↦CX 5. △ ABC B a C

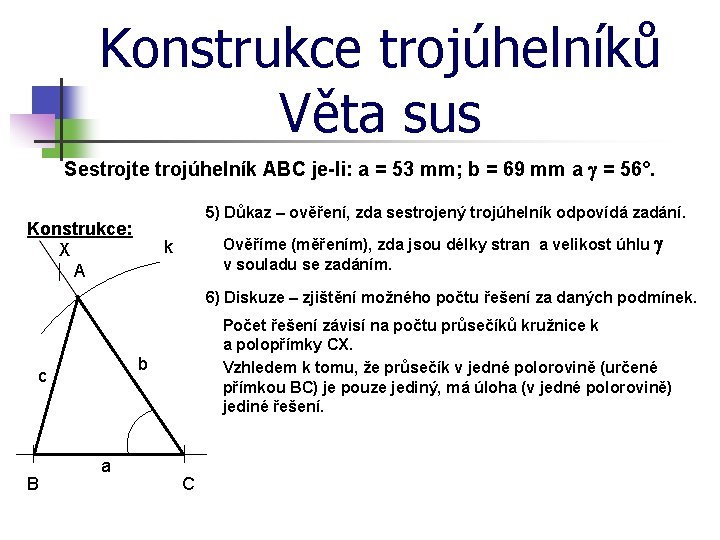
Konstrukce trojúhelníků Věta sus Sestrojte trojúhelník ABC je-li: a = 53 mm; b = 69 mm a = 56°. 5) Důkaz – ověření, zda sestrojený trojúhelník odpovídá zadání. Konstrukce: X A Ověříme (měřením), zda jsou délky stran a velikost úhlu v souladu se zadáním. k 6) Diskuze – zjištění možného počtu řešení za daných podmínek. b c B Počet řešení závisí na počtu průsečíků kružnice k a polopřímky CX. Vzhledem k tomu, že průsečík v jedné polorovině (určené přímkou BC) je pouze jediný, má úloha (v jedné polorovině) jediné řešení. a C

Konstrukce trojúhelníků Věta usu Sestrojte trojúhelník ABC je-li: a = 53 mm; b = 69° a = 56°. 1) Pozorně si přečteme a analyzujeme zadání úlohy. Abychom trojúhelník mohli sestrojit musí být součet velikostí zadaných úhlů menší než 180°. b + < 180° 69° + 56° < 180° 125° < 180°

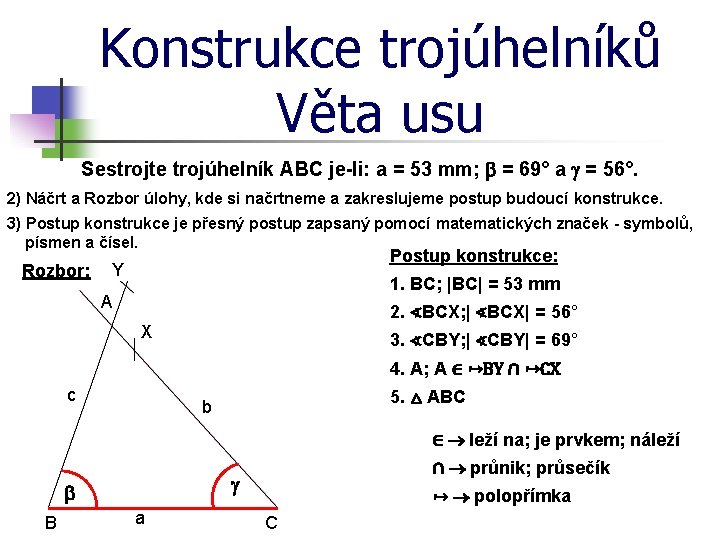
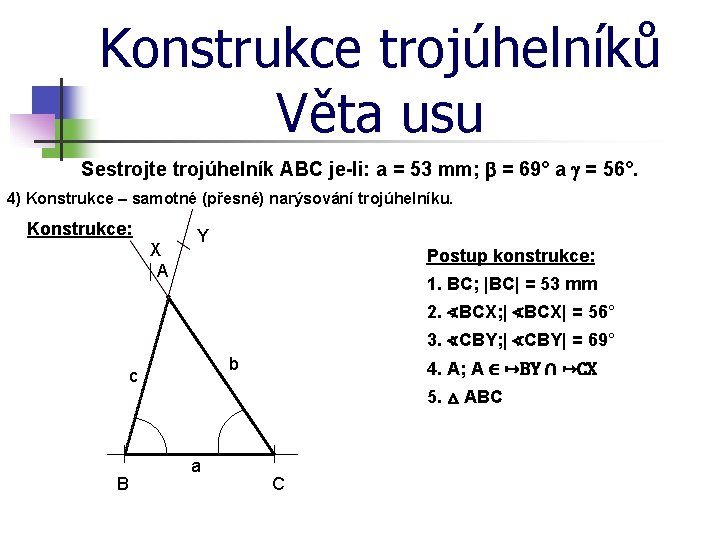
Konstrukce trojúhelníků Věta usu Sestrojte trojúhelník ABC je-li: a = 53 mm; b = 69° a = 56°. 2) Náčrt a Rozbor úlohy, kde si načrtneme a zakreslujeme postup budoucí konstrukce. 3) Postup konstrukce je přesný postup zapsaný pomocí matematických značek - symbolů, písmen a čísel. Rozbor: Postup konstrukce: Y 1. BC; |BC| = 53 mm A 2. ∢BCX; | ∢BCX| = 56° X 3. ∢CBY; | ∢CBY| = 69° 4. A; A ∈ ↦BY ∩ ↦CX c 5. △ ABC b ∈ leží na; je prvkem; náleží b B ∩ průnik; průsečík a ↦ polopřímka C

Konstrukce trojúhelníků Věta usu Sestrojte trojúhelník ABC je-li: a = 53 mm; b = 69° a = 56°. 4) Konstrukce – samotné (přesné) narýsování trojúhelníku. Konstrukce: X A Y Postup konstrukce: 1. BC; |BC| = 53 mm 2. ∢BCX; | ∢BCX| = 56° 3. ∢CBY; | ∢CBY| = 69° b c 4. A; A ∈ ↦BY ∩ ↦CX 5. △ ABC B a C

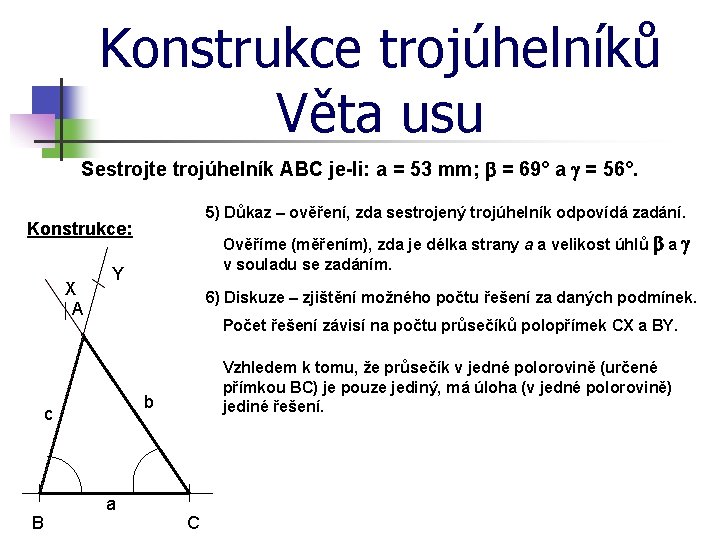
Konstrukce trojúhelníků Věta usu Sestrojte trojúhelník ABC je-li: a = 53 mm; b = 69° a = 56°. 5) Důkaz – ověření, zda sestrojený trojúhelník odpovídá zadání. Konstrukce: X A Y 6) Diskuze – zjištění možného počtu řešení za daných podmínek. Počet řešení závisí na počtu průsečíků polopřímek CX a BY. Vzhledem k tomu, že průsečík v jedné polorovině (určené přímkou BC) je pouze jediný, má úloha (v jedné polorovině) jediné řešení. b c B Ověříme (měřením), zda je délka strany a a velikost úhlů b a v souladu se zadáním. a C

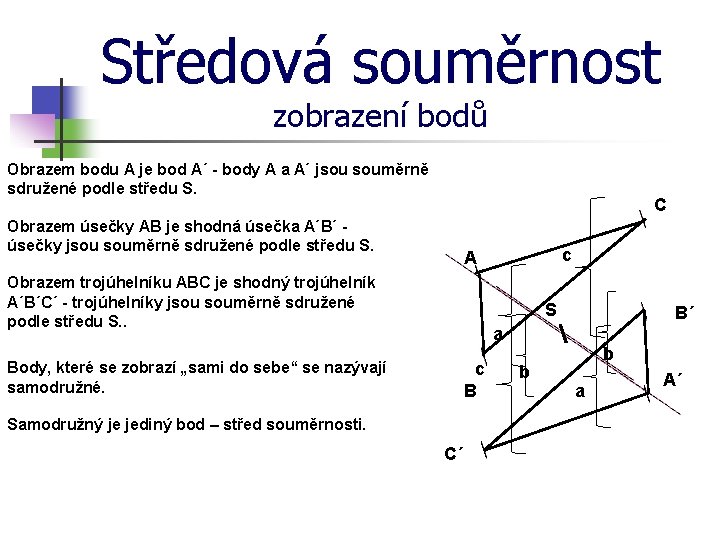
Středová souměrnost zobrazení bodů Obrazem bodu A je bod A´ - body A a A´ jsou souměrně sdružené podle středu S. C Obrazem úsečky AB je shodná úsečka A´B´ úsečky jsou souměrně sdružené podle středu S. c A Obrazem trojúhelníku ABC je shodný trojúhelník A´B´C´ - trojúhelníky jsou souměrně sdružené podle středu S. . S B´ a c B Body, které se zobrazí „sami do sebe“ se nazývají samodružné. Samodružný je jediný bod – střed souměrnosti. C´ b b a A´

Středová souměrnost je dána středem souměrnosti. Středová souměrnost je shodné zobrazení tj. vzor i obraz jsou shodné geometrické útvary. Středová souměrnost má jediný samodružný bod (bod, který se zobrazí sám do sebe). Tímto bodem je střed souměrnosti. Úsečka a její obraz ve středové souměrnosti jsou shodné a rovnoběžné úsečky.

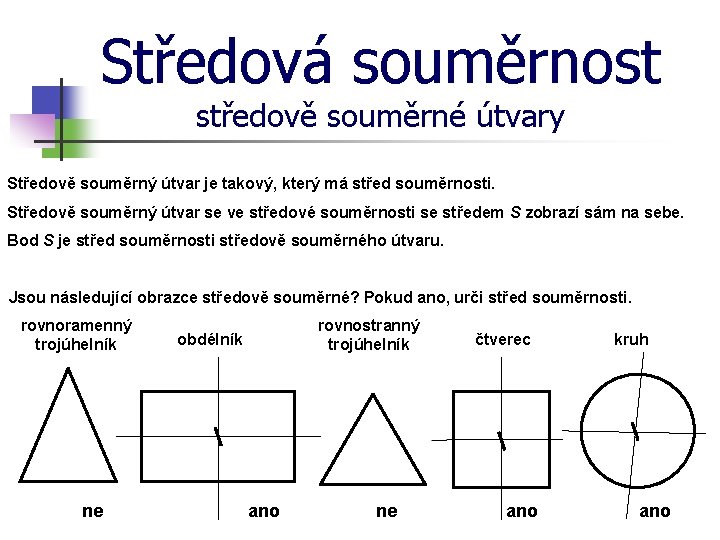
Středová souměrnost středově souměrné útvary Středově souměrný útvar je takový, který má střed souměrnosti. Středově souměrný útvar se ve středové souměrnosti se středem S zobrazí sám na sebe. Bod S je střed souměrnosti středově souměrného útvaru. Jsou následující obrazce středově souměrné? Pokud ano, urči střed souměrnosti. rovnoramenný trojúhelník ne rovnostranný trojúhelník obdélník ano ne čtverec ano kruh ano