Salir TRIGONOMETRA ESFRICA l MOTIVACIN Aplicacin en Geodesia






















- Slides: 39

Salir TRIGONOMETRÍA ESFÉRICA l MOTIVACIÓN: Aplicación en Geodesia (2º) y Métodos Topográficos (2º) l. Lección 1: Geometría sobre la superficie esférica. l. Lección 2: Relaciones entre los lados y los ángulos de un triángulo • Definiciones • Triángulos esféricos. Triangulo polar • Propiedades de los triángulos esféricos • Área de un triángulo esférico (demostrar) esférico. • Fórmulas de Bessel • Teorema del seno (demostrar) • Teorema del coseno • Teorema de la cotangente • Teorema del coseno para los ángulos • Funciones del ángulo mitad. Analogías de Gauss-Delambre • Analogías de Neper l. Lección 3: Distancia esférica. Triángulos esféricos rectángulos y rectiláteros. • Distancia esférica. Rumbo • Triángulos esféricos rectángulos • Propiedades de los triángulos esféricos rectángulos (alguna demostración) • Triángulos esféricos rectiláteros 1

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Lección 2: Relaciones entre los lados y los ángulos de un triángulo esférico. l Fórmulas de Bessel: teorema del seno para lados, teorema del coseno para lados, teorema de la cotangente, teorema del coseno para ángulos(haremos alguna demostración) l Fórmulas de Briggs. Analogías de Gauss-Delambre. Analogías de Neper. l Distancia esférica entre dos puntos(conociendo latitud y longitud de ambos puntos) 2 Índice

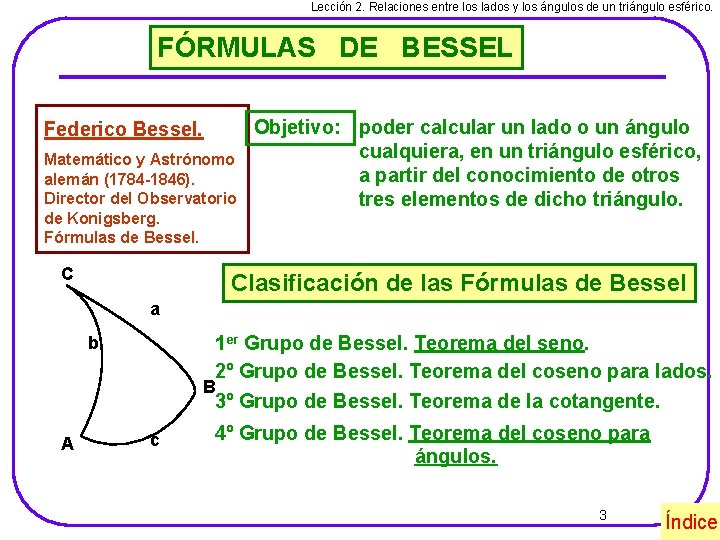
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. FÓRMULAS DE BESSEL Federico Bessel. Matemático y Astrónomo alemán (1784 -1846). Director del Observatorio de Konigsberg. Fórmulas de Bessel. C Objetivo: poder calcular un lado o un ángulo cualquiera, en un triángulo esférico, a partir del conocimiento de otros tres elementos de dicho triángulo. Clasificación de las Fórmulas de Bessel a 1 er Grupo de Bessel. Teorema del seno. 2º Grupo de Bessel. Teorema del coseno para lados. b B 3º Grupo de Bessel. Teorema de la cotangente. A c 4º Grupo de Bessel. Teorema del coseno para ángulos. 3 Índice

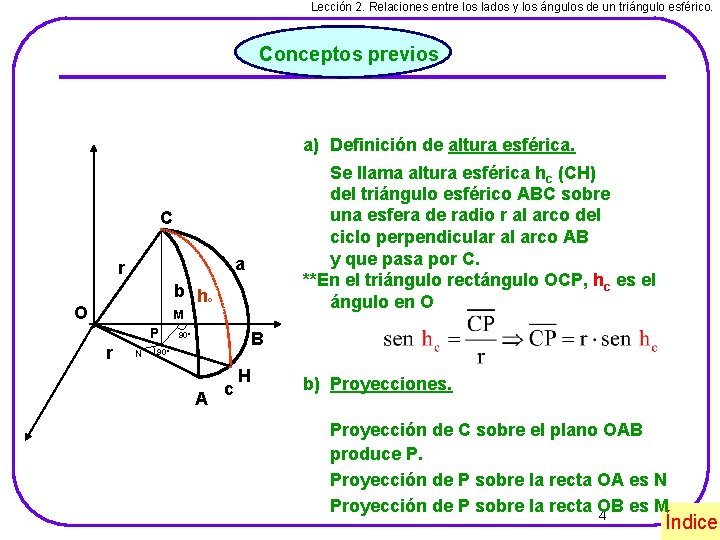
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Conceptos previos a) Definición de altura esférica. Se llama altura esférica hc (CH) del triángulo esférico ABC sobre una esfera de radio r al arco del ciclo perpendicular al arco AB y que pasa por C. **En el triángulo rectángulo OCP, hc es el ángulo en O C a r b hc O M P r N B 90º A c H b) Proyecciones. Proyección de C sobre el plano OAB produce P. Proyección de P sobre la recta OA es N Proyección de P sobre la recta OB es M 4 Índice

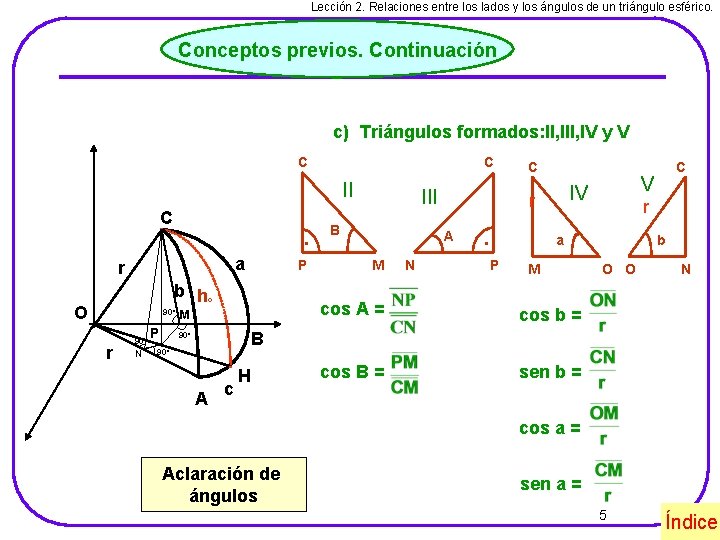
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Conceptos previos. Continuación c) Triángulos formados: II, IV y V C C II C . a r P b hc O 90º r 90º N P M III B N . P r b a M cos A = cos b = cos B = sen b = C V IV r A M C O O N B 90º A c H cos a = Aclaración de ángulos sen a = 5 Índice

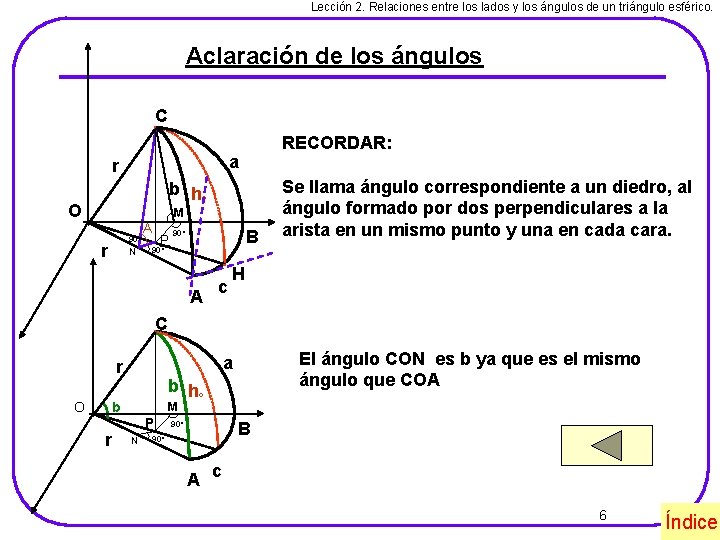
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Aclaración de los ángulos C RECORDAR: a r b hc O M 90º r N A P B 90º A c Se llama ángulo correspondiente a un diedro, al ángulo formado por dos perpendiculares a la arista en un mismo punto y una en cada cara. H C O b hc b r El ángulo CON es b ya que es el mismo ángulo que COA a r M P N B 90º A c 6 Índice

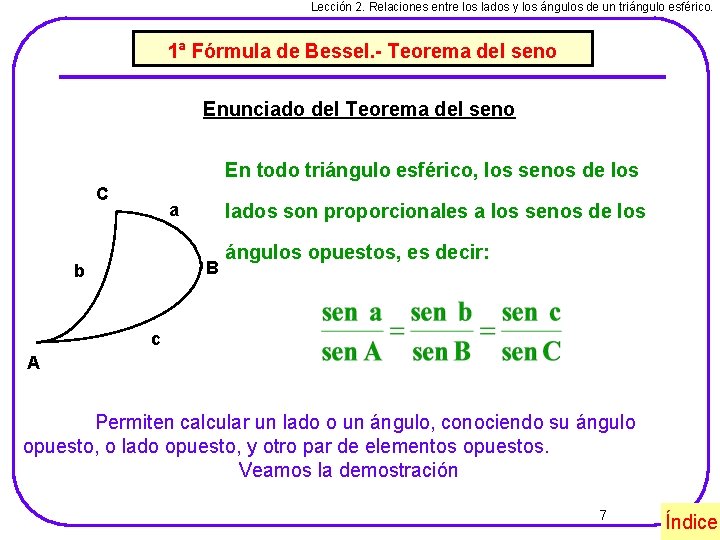
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. 1ª Fórmula de Bessel. - Teorema del seno Enunciado del Teorema del seno En todo triángulo esférico, los senos de los C a lados son proporcionales a los senos de los B b ángulos opuestos, es decir: c A Permiten calcular un lado o un ángulo, conociendo su ángulo opuesto, o lado opuesto, y otro par de elementos opuestos. Veamos la demostración 7 Índice

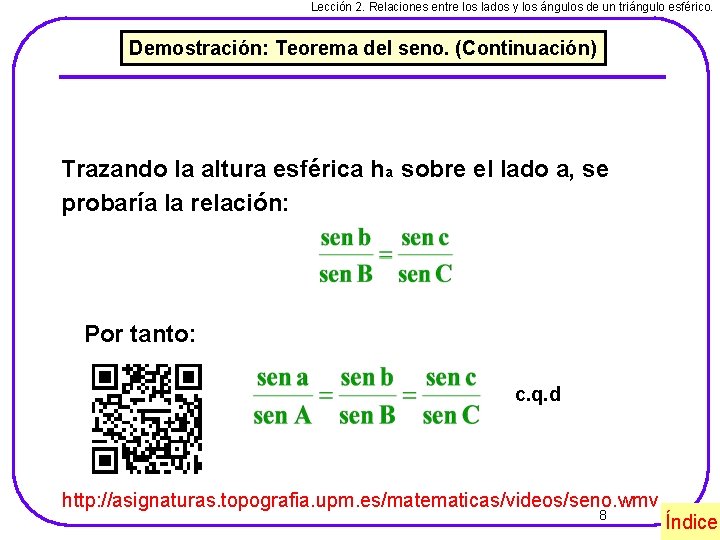
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Demostración: Teorema del seno. (Continuación) Trazando la altura esférica ha sobre el lado a, se probaría la relación: Por tanto: c. q. d http: //asignaturas. topografia. upm. es/matematicas/videos/seno. wmv 8 Índice

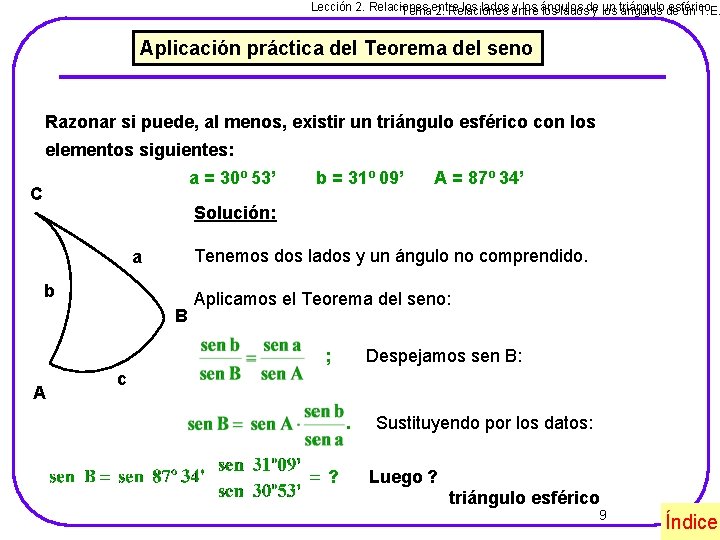
Lección 2. Relaciones los lados entre y los ángulos un triángulo esférico. Temaentre 2. Relaciones los ladosde y los ángulos de un T. E. Aplicación práctica del Teorema del seno Razonar si puede, al menos, existir un triángulo esférico con los elementos siguientes: a = 30º 53’ C b = 31º 09’ A = 87º 34’ Solución: Tenemos dos lados y un ángulo no comprendido. a b B Aplicamos el Teorema del seno: ; A Despejamos sen B: c. ? Sustituyendo por los datos: Luego ? triángulo esférico 9 Índice

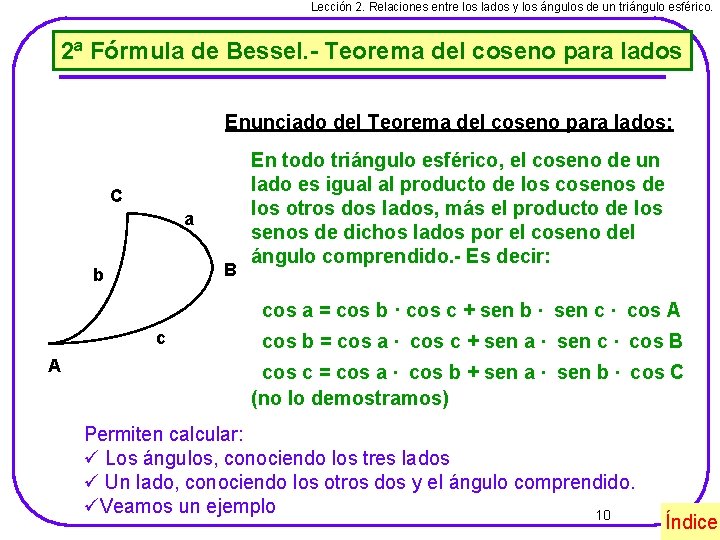
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. 2ª Fórmula de Bessel. - Teorema del coseno para lados Enunciado del Teorema del coseno para lados: C a B b En todo triángulo esférico, el coseno de un lado es igual al producto de los cosenos de los otros dos lados, más el producto de los senos de dichos lados por el coseno del ángulo comprendido. - Es decir: cos a = cos b · cos c + sen b · sen c · cos A cos b = cos a · cos c + sen a · sen c · cos B cos c = cos a · cos b + sen a · sen b · cos C (no lo demostramos) Permiten calcular: ü Los ángulos, conociendo los tres lados ü Un lado, conociendo los otros dos y el ángulo comprendido. üVeamos un ejemplo 10 Índice

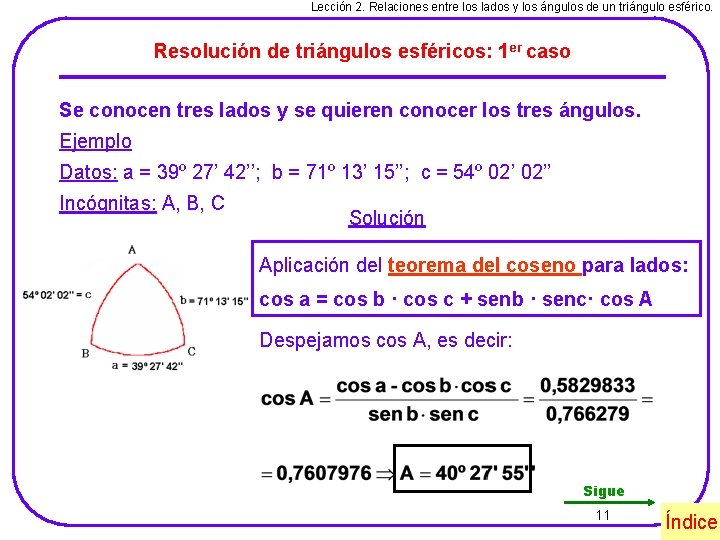
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esféricos: 1 er caso Se conocen tres lados y se quieren conocer los tres ángulos. Ejemplo Datos: a = 39º 27’ 42’’; b = 71º 13’ 15’’; c = 54º 02’’ Incógnitas: A, B, C Solución Aplicación del teorema del coseno para lados: cos a = cos b · cos c + senb · senc· cos A Despejamos cos A, es decir: Sigue 11 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esféricos: 1 er caso Ángulo B: Ángulo C: Propiedades triángulos esféricos Sigue 12 Índice

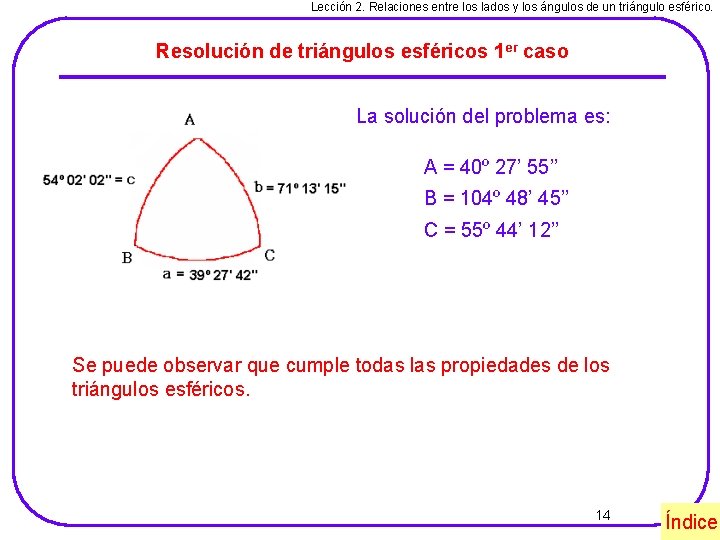
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esféricos 1 er caso La solución del problema es: A = 40º 27’ 55’’ B = 104º 48’ 45’’ C = 55º 44’ 12’’ Se puede observar que cumple todas las propiedades de los triángulos esféricos. 14 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. 3ª Fórmula de Bessel. - Teorema de la cotangente cot a sen b = cos b cos C + sen C cot A cot a sen c = cos c cos B + sen B cot A cot b sen a = cos a cos C + sen C cot B cot b sen c = cos c cos A + sen A cot B cot c sen a = cos a cos B + sen B cot C cot c sen b = cos b cos A + sen A cot C (no las utilizaremos demasiado) 15 Índice

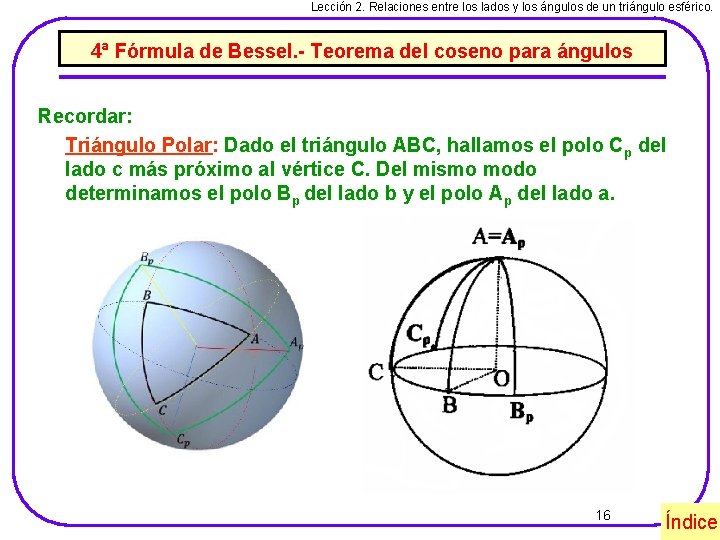
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. 4ª Fórmula de Bessel. - Teorema del coseno para ángulos Recordar: Triángulo Polar: Dado el triángulo ABC, hallamos el polo Cp del lado c más próximo al vértice C. Del mismo modo determinamos el polo Bp del lado b y el polo Ap del lado a. 16 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. 4ª Fórmula de Bessel. - Teorema del coseno para ángulos Aplicando el Teorema del Coseno para lados al triángulo polar ABC, se tiene: cos ap = cos bp cos cp + sen bp sen cp cos Ap Por tanto: cos(180º - A) = cos(180º - B) cos(180º - C) + sen(180º - B) sen(180º - C) cos(180º - a) Simplificando: - cos A = (- cos B) (- cos C) + sen B sen C ( - cos a) Multiplicando la igualdad por (-1): cos A = - cos B cos C + sen B sen C · cos a Sigue 17 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Teorema del coseno para ángulos (continuación) Obteniéndose las fórmulas que relacionan tres ángulos y un lado: cos A = - cos B cos C + sen B sen C cos a cos B = - cos A cos C + sen A sen C cos b cos C = - cos A cos B + sen A sen B cos c Permiten calcular: ü Los lados, conociendo los tres ángulos ü Un ángulo y un lado , conociendo dos ángulos y el lado comprendido. üVeamos un ejemplo 18 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esféricos: 2º caso Se conocen tres ángulos y se quiere calcular los tres lados: Ejemplo Datos: A = B = 52º 14’ 24’’; C = 82º 12’ 03’’ Incógnitas: a, b, c Solución Comprobamos que se trata de un triángulo esférico: A + B + C = 186º 40’ 51’’ Luego: 180º < A + B + C < 540º Para resolver este 2º caso se aplica el teorema del coseno para ángulos cos A = - cos B · cos C + sen B · sen C· cos a. Sigue 19 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esféricos: 2º caso Se despeja cos a del teorema del coseno para ángulos: Como A = B a = b. Luego: b = ? Se aplica otra vez el teorema del coseno para ángulos, esta vez para el ángulo C: cos C = - cos A · cos B + sen A · sen B· cos c. Despejamos c y nos queda: Se puede observar que cumple todas las propiedades de los triángulos esféricos. Propiedades triángulos esféricos 20 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Funciones del ángulo mitad a + b + c = 2 p (perímetro) Efectuando el cociente, se tiene: Estas fórmulas permiten calcular los ángulos de un triángulo esférico, conocidos tres lados o bien el perímetro y dos lados. 21 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Ejemplo de aplicación de las Funciones del ángulo mitad En un triángulo isósceles los lados miden: b = c = 60º, a = 90º. Calcular A, B y C Solución Sigue 22 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Ejemplo de aplicación de las Funciones del ángulo mitad Cálculo de B: Teorema del Seno(calcular) Y como b= c también B=C C = B = 54º 44’ 08” ; A = 109º 28’ 16” 23 Índice

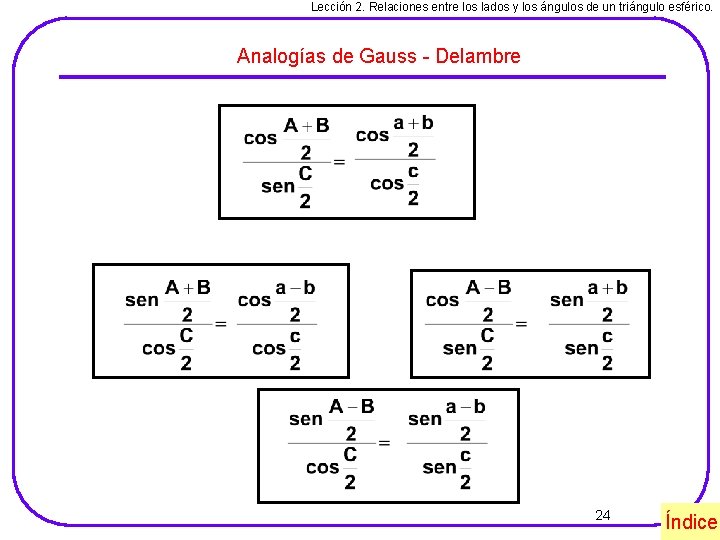
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Analogías de Gauss - Delambre 24 Índice

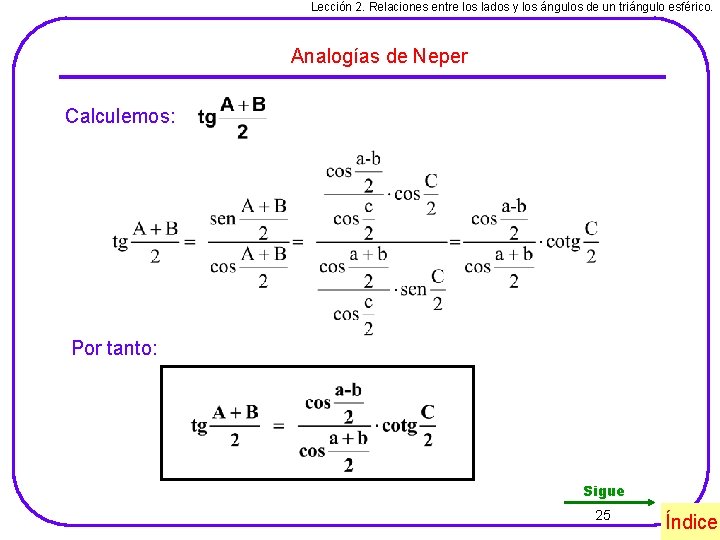
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Analogías de Neper Calculemos: Por tanto: Sigue 25 Índice

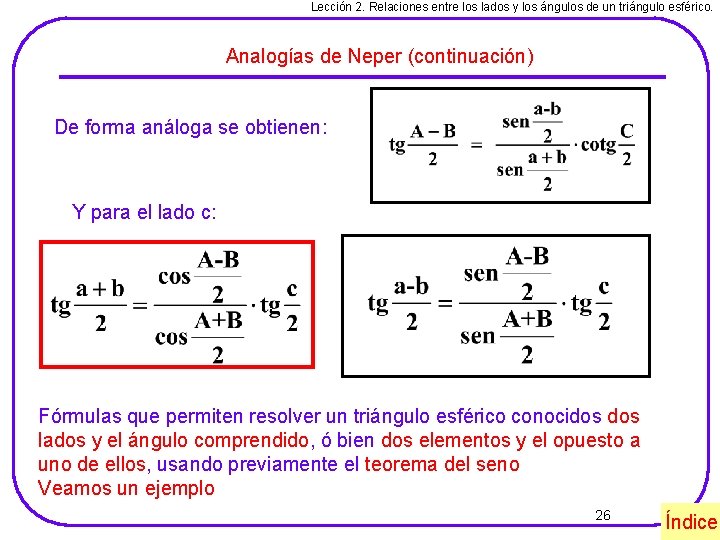
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Analogías de Neper (continuación) De forma análoga se obtienen: Y para el lado c: Fórmulas que permiten resolver un triángulo esférico conocidos lados y el ángulo comprendido, ó bien dos elementos y el opuesto a uno de ellos, usando previamente el teorema del seno Veamos un ejemplo 26 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esférico: 5º caso Se conocen dos lados y el ángulo opuesto a uno de ellos. Ejemplo Datos: a = 42º 42’ 12’’; A = 37º 45’; b = 65º 36’ Incógnitas: B, C, c Solución En este caso disponemos de dos valores como posibles soluciones. Se darán los siguientes pasos: 1. Se aplica el teorema del seno para calcular el ángulo B y decidiremos si tiene 1 ó 2 soluciones (según las propiedades de los triángulos esféricos). 2. Se aplica las fórmulas de Neper para calcular el lado c. 3. Se aplica el teorema del coseno para lados para calcular el ángulo C, Sigue 27 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esférico: 5º caso Teorema del seno para calcular el ángulo B: Sustituyendo los datos sen B = ? ? Hay dos posibles soluciones ya que el seno es positivo en el 1 er cuadrante y el 2º cuadrante, siendo ambas soluciones menores que 180º. Estas soluciones son: B 1 = ? ; B 2 = (180º -B 1 )= ? ¿Son válidas ambas soluciones? Se tiene que comprobar la propiedad de los triángulos esféricos: En este caso a < b A = 37º 45’ < B, pero esto lo cumplen ambos ángulos Hay dos soluciones(dos triángulos) Sigue 28 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esférico: 5º caso Primera solución Datos: a = 42º 42’ 12’’; A = 37º 45’; b = 65º 36’; B 1= 55º 17’ 36’’ Incógnitas: c 1, C 1 Solución: Para calcular el lado c 1, aplicamos la fórmula de Neper: Despejando: Cálculos: Sigue 29 Índice

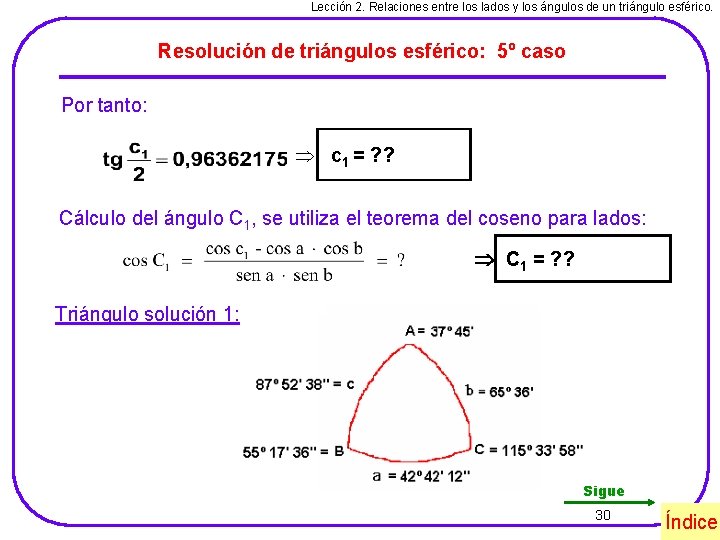
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esférico: 5º caso Por tanto: c 1 = ? ? Cálculo del ángulo C 1, se utiliza el teorema del coseno para lados: C 1 = ? ? Triángulo solución 1: Sigue 30 Índice

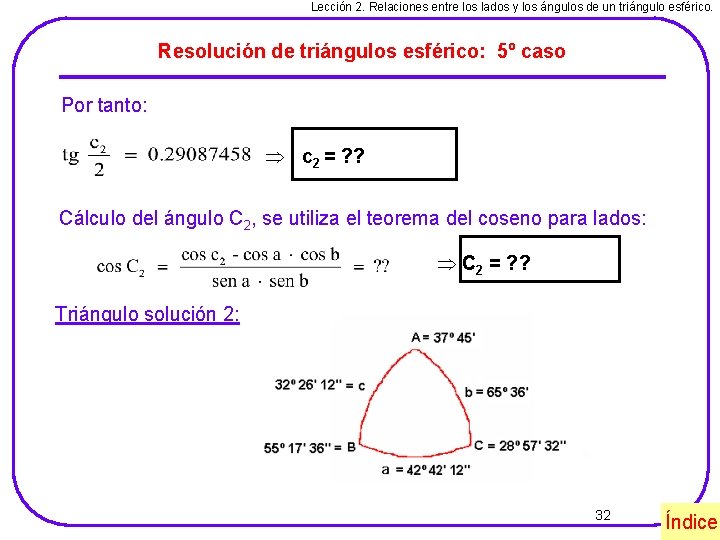
Lección 2. Relaciones los lados entre y los ángulos un triángulo esférico. Temaentre 2. Relaciones los ladosde y los ángulos de un T. E. Resolución de triángulos esférico: 5º caso Segunda solución: propuesto Datos: a = 42º 42’ 12’’; A = 37º 45’; b = 65º 36’; B 2= 124º 42’ 23’’ Incógnitas: c 2, C 2 Solución: Para calcular el lado c 2, aplicamos la fórmula de Neper: Cálculos: Sigue 31 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esférico: 5º caso Por tanto: c 2 = ? ? Cálculo del ángulo C 2, se utiliza el teorema del coseno para lados: C 2 = ? ? Triángulo solución 2: 32 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esféricos: resumen de casos (ver fotocopia con todos los casos) Resolver un triángulo esférico es conocer sus tres lados y sus tres ángulos. Se pueden presentar los siguientes casos: 1. Se conocen tres lados. 2. Se conocen tres ángulos. 3. Se conocen dos lados y el ángulo comprendido. 4. Se conocen dos ángulos y el lado comprendido. 5. Se conocen dos lados y el ángulo opuesto a uno de ellos. 6. Se conocen dos ángulos y el lado opuesto a uno de ellos 33 ¡¡¡VAMOS A PRACTICAR CON LA HOJA DE PROBLEMAS!! Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esférico: 3º caso Se conocen dos lados y el ángulo comprendido. Ejemplo Datos: a = 73º 58’’; b = 38º 45’ 00’’; C = 46º 33’ 41’’ Incógnitas: A, B, c Solución Para resolver este caso se utiliza el teorema del coseno para lados. En este ejemplo se aplica dicho teorema para calcular el lado c. Una vez calculado el lado c, se vuelve aplicar dicho teorema para calcular los ángulos A y B Sigue 34 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esférico: 3º caso Teorema del coseno para lados: cos c = cos a · cos b + sen a · sen b · cos C. Sustituyendo los datos nos queda: cos c = 0, 62885370 c = 51º 02’ 03’’ • Ahora ya conocemos los tres lados. Se vuelve aplicar el teorema del coseno para lados. cos a = cos b · cos c + sen b · sen c · cos A despejando cos A, se tiene: cos A = - 0, 440764432 A = 116º 09’ 9’’ • Cálculo del ángulo B. cos b = cos a · cos c + sen a · sen c · cos B despejando cos B, se tiene: cos B = 0, 81136809103 B = 35º 46’ 12’’ 35 Índice

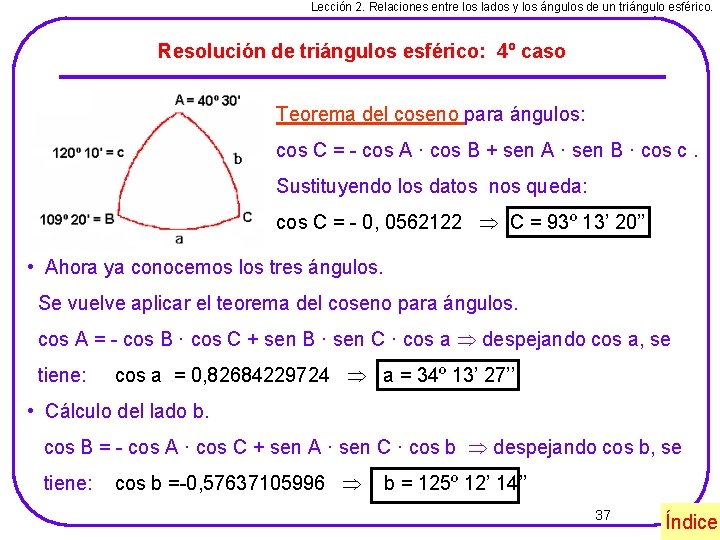
Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esférico: 4º caso Se conocen dos ángulos y el lado comprendido. Ejemplo. Datos: A = 40º 30’; B = 109º 20’; c = 120º 10’ Incógnitas: C, a, b. Solución Para resolver este caso se utiliza el teorema del coseno para ángulos. En este ejemplo se aplica dicho teorema para calcular el ángulo C. Una vez calculado el ángulo C, se vuelve aplicar dicho teorema para calcular los lados a y b. Sigue 36 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esférico: 4º caso Teorema del coseno para ángulos: cos C = - cos A · cos B + sen A · sen B · cos c. Sustituyendo los datos nos queda: cos C = - 0, 0562122 C = 93º 13’ 20’’ • Ahora ya conocemos los tres ángulos. Se vuelve aplicar el teorema del coseno para ángulos. cos A = - cos B · cos C + sen B · sen C · cos a despejando cos a, se tiene: cos a = 0, 82684229724 a = 34º 13’ 27’’ • Cálculo del lado b. cos B = - cos A · cos C + sen A · sen C · cos b despejando cos b, se tiene: cos b =-0, 57637105996 b = 125º 12’ 14’’ 37 Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esférico: 6º caso Se conocen dos ángulos y el lado opuesto a uno de ellos. Ejemplo Datos: C = 42º 12’ 20’’; B = 83º 34’ 15’’ ; b = 74º 18’ 02’’ Incógnitas: a, c y A Solución En este caso disponemos de dos valores como posibles soluciones. Se darán los siguientes pasos: 1. Se aplica el teorema del seno para calcular el lado c y decidiremos si tiene 1 ó 2 soluciones (según las propiedades de los triángulos esféricos). 2. Se aplica las fórmulas de Neper para calcular el lado a. 3. Se aplica el teorema del coseno para lados para calcular el ángulo A, Sigue 38 Índice

Lección 2. Relaciones los lados entre y los ángulos un triángulo esférico. Temaentre 2. Relaciones los ladosde y los ángulos de un T. E. Resolución de triángulos esférico: 6º caso Teorema del seno para calcular el lado c: = 0, 65082377777 Puede haber dos soluciones: c 1 = 40º 36’ 13’’ y c 2 = (180º - 40º 36’ 13’’) = 139º 23’ 46’’ ¿Son válidas ambas soluciones? Se tiene que comprobar la propiedad de los triángulos esféricos: B > C b > c, esta propiedad solo se cumple para la 1ª solución. Luego rechazamos c 2 = 139º 23’ 46’’ 39 Sigue Índice

Lección 2. Relaciones entre los lados y los ángulos de un triángulo esférico. Resolución de triángulos esférico: 6º caso Solución única del problema: Datos: C = 42º 12’ 20’’; B = 83º 34’ 15’’ ; b = 74º 18’ 02’’; c = 40º 36’ 13’’ Incógnita: a, A. • Analogía de Neper para el lado a: = 0, 76322043565 = 37º 21’ 6’’ a = 74º 42’ 11’’ • Cálculo del ángulo A, mediante el teorema del coseno para lados: A = 84º 39’ 13’’ 40 Índice
 Aplicacin
Aplicacin Motivacin
Motivacin Qu es la motivacion
Qu es la motivacion Motivacin
Motivacin Motivacin
Motivacin La teoría de motivación-higiene de herzberg:
La teoría de motivación-higiene de herzberg: Razones trigonometricas de 30 45 60
Razones trigonometricas de 30 45 60 Cotangentoide
Cotangentoide Coseno de 30
Coseno de 30 Seno
Seno Trigonometra
Trigonometra Introduccion de trigonometria
Introduccion de trigonometria Triangulo notable de 45
Triangulo notable de 45 λa
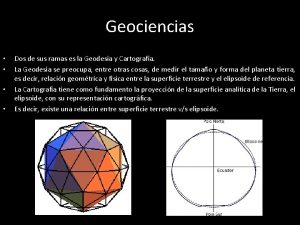
λa Ramas de la geodesia
Ramas de la geodesia Geodesia
Geodesia Mirante de geodésia
Mirante de geodésia Commands in spanish tu
Commands in spanish tu Jaime y maria acuerdan salir en bicicleta
Jaime y maria acuerdan salir en bicicleta Salir de este juego
Salir de este juego Primeras en entrar primeras en salir
Primeras en entrar primeras en salir Contigo conmigo senor wooly
Contigo conmigo senor wooly Cancer aguda grave o esdrujula
Cancer aguda grave o esdrujula Saludo al entrar y me despido al salir
Saludo al entrar y me despido al salir Salir subjunctive
Salir subjunctive Oir yo form
Oir yo form Pido infinitive
Pido infinitive Salir mandatos formales
Salir mandatos formales Desinencia verbal
Desinencia verbal Spanish verbs with irregular yo forms
Spanish verbs with irregular yo forms Cierre la puerta al salir
Cierre la puerta al salir Image past
Image past Fornicaciòn en la biblia
Fornicaciòn en la biblia Amigux
Amigux Celebrar fiesta en el desierto
Celebrar fiesta en el desierto Forms of decir
Forms of decir Salir formal command
Salir formal command Modelo salir
Modelo salir Salir formal command
Salir formal command