Ruang sampel Kejadian Menghitung titik sampel Peluang suatu

Ruang sampel Kejadian Menghitung titik sampel Peluang suatu kejadian Aturan penjumlahan Peluang bersyarat Aturan perkalian Aturan Bayes

SAMPEL Himpunan semua hasil yang mungkin dari suatu percobaan statistika disebut ruang sampel dan dinyatakan dengan lambang T. Contoh: Ruang sampel sebuah dadu adalah: T = { 1, 2, 3, 4, 5, 6 }

Suatu kejadian adalah himpunan bagian dari ruang sampel. Contoh: Kejadian A adalah hasil lemparan suatu dadu yang dapat dibagi tiga. Maka hasilnya adalah A = { 3, 6 }

Komplemen suatu kejadian A terhadap T ialah himpunan semua unsur T yang tidak termasuk A. Komplemen A dinyatakan dengan lambang A’. Contoh : Komplemen dari A = { 3, 6 } pada lemparan sebuah dadu adalah A’ = { 1, 2, 4, 5 }

Irisan dua kejadian A dan B, dinyatakan dengan lambang A ∩ B, ialah kejadian yang unsurnya termasuk dalam A dan B. Contoh: Pada lemparan sebuah dadu, misalkan A kejadian bahwa bilangan genap yang muncul dan B kejadian bahwa bilangan lebih besar dari 3 yang muncul. Maka A = {2, 4, 6} dan B = {4, 5, 6} sehingga A ∩ B = {4, 6}

Gabungan dua kejadian A dan B, dinyatakan dengan lambang A U B, ialah kejadian yang mengandung semua unsur yang termasuk A atau B atau keduanya. Contoh: A = { a, b, c } dan B = { b, c, d, e} maka A U B = { a, b, c, d, e }

Bila suatu operasi dapat dilakukan dengan n 1 cara, dan bila untuk tiap cara ini operasi kedua dapat dikerjakan dengan n 2 cara, dan seterusnya, maka deretan k operasi dapat dikerjakan bersama-sama dengan n 1 n 2…nk cara

Suatu permutasi adalah urutan yang berbeda -beda yang dapat dibentuk dari sekumpulan benda. Contoh: Dari tiga huruf a, b, c, permutasi yang dapat dibuat adalah abc, acb, bac, bca, cab, dan cba. Banyaknya permutasi n benda yang berlainan adalah n! Seperti contoh diatas, permutasi tiga huruf adalah 3! = (3)(2)(1) = 6

Banyaknya permutasi n benda berlainan bila diambil r sekaligus adalah Contoh: Dari 20 lotere, dua diambil untuk hadiah pertama dan kedua. Banyak titik sampel = = (20)(19) = 380

Banyaknya permutasi n benda berlainan yang disusun melingkar adalah ( n - 1 )! Banyaknya permutasi yang berlainan dari n benda bila diantaranya berjenis pertama, berjenis kedua, …. , berjenis ke k adalah Contoh: Ada berapa cara menyusun 9 lampu pohon Natal bila 3 diantaranya berwarna merah, 4 kuning, dan 2 biru? Banyaknya susunan yang berlainan adalah = 1260 cara

Pemilihan r benda dari sejumlah n tanpa memperdulikan urutannya disebut kombinasi. Contoh: Jika ada 4 kimiawan dan 3 fisikawan, banyaknya cara memilih kelompok yang terdiri 2 kimiawan dan 1 fisikawan adalah:

Peluang suatu kejadian A adalah jumlah bobot semua titik sampel yang termasuk A. Jadi 0 ≤ P(A) ≤ 1, P(Ø) = 0, dan P(T) = 1 Contoh: Sebuah mata uang dilempar dua kali. Berapa peluang paling sedikit muncul muka sekali? Ruang sampelnya adalah T = { MM, MB, BM, BB } maka tiap titik sampel memiliki bobot = ¼ Bila A menyatakan kejadian bahwa paling sedikit satu muka muncul, maka A = { MM, MB, BM } P(A)= ¼ + ¼ = 3/4 Jadi peluangnya paling sedikit muncul muka sekali adalah ¾

Bila A dan B dua kejadian sembarang, maka P(A U B) = P(A) + P(B) – P(A ∩ B) Bila A dan B kejadian yang terpisah, maka P(A U B) = P(A) + P(B) Untuk tiga kejadian A, B, dan C P(A U B U C) = P(A) + P(B) + P(C) – P(A ∩ B) P(A ∩ C) - P(B ∩ C) + P(A ∩ B ∩ C)

Peluang seorang mahasiswa lulus matematika 2/3 dan peluangnya lulus biologi 4/9. Bila peluangnya lulus kedua mata kuliah ¼, berapakah peluangnya lulus paling sedikit satu mata kuliah? Jawab: Bila M menyatakan kejadian “lulus matematika” dan B “lulus biologi” maka P(M U B) = P(M) + P(B) – P(M ∩ B) = 2/3 + 4/9 – ¼ = 31/36

Peluang terjadinya suatu kejadian B bila diketahui bahwa kejadian A telah terjadi disebut peluang bersyarat dan dinyatakan dengan P(B|A) = bila P(A) >0

Peluang suatu penerbangan yang telah terjadwal teratur berangkat tepat waktu P(B) = 0, 83; peluang sampai tepat waktu P(S) = 0, 82 dan peluang berangkat dan sampai tepat waktu P(B ∩ S) = 0, 78. Peluang pesawat sampai tepat waktu jika diketahui berangkat tepat waktu P(S|B)= = = 0, 94

P(A|B) = P(A) Terjadinya B sama sekali tidak mempengaruhi terjadinya A. Dua kejadian A dan B bebas jika dan hanya jika P(B|A) = P(B) dan P(A|B) = P(A) jika tidak demikian, A dan B tak bebas.

Pengambilan dua kartu yang diambil berturutan dari sekotak kartu dengan pengembalian. A = kartu pertama yang terambil as B = kartu kedua sebuah skop Karena kartu pertama dikembalikan, ruang sampel untuk kedua pengambilan terdiri atas 52 kartu. P(B|A) = 13/52 = ¼ P(B) = 13/52 = ¼ Jadi, P(B|A) = P(B) Kejadian A dan B dikatakan bebas.

Bila kejadian A dan B dapat terjadi pada suatu percobaan, maka P(A∩B) = P(A) P(B|A) Jadi peluang A dan B terjadi serentak sama dengan peluang A terjadi dikalikan dengan peluang terjadinya B bila A terjadi. Karena kejadian A∩B dan B∩A ekivalen maka tidaklah menjadi soal kejadian mana yang disebut A dan yang disebut B.

Jika kita memiliki kotak berisi 20 sekering, 5 diantaranya cacat. Bila 2 sekering dikeluarkan dari kotak satu demi satu secara acak (tanpa mengembalikan yang pertama ke dalam kotak), berapakah peluang kedua sekering itu cacat? Jawab A = kejadian bahwa sekering pertama cacat B = kejadian bahwa yang kedua cacat A∩B = kejadian bahwa A terjadi dan kemudian B terjadi setelah A terjadi. P(A) = 5/20 = ¼ P(B|A) = 4/19 P(A∩B) = (1/4) (4/19) = 1/19

Dua kejadian A dan B bebas jika dan hanya jika P(A∩B) = P(A) P(B) Contoh : Suatu kota memiliki 1 mobil pemadam kebakaran dan 1 ambulans. Peluang mobil pemadam kebakaran siap waktu diperlukan 0, 98, peluang ambulans siap waktu dipanggil 0, 92. Peluang keduanya siap adalah P(A∩B) = P(A) P(B) = (0, 98) (0, 92) = 0, 9016

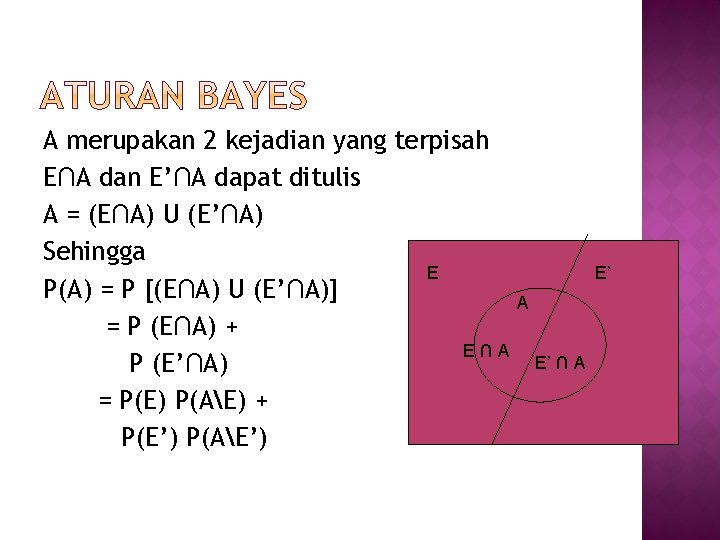
A merupakan 2 kejadian yang terpisah E∩A dan E’∩A dapat ditulis A = (E∩A) U (E’∩A) Sehingga E P(A) = P [(E∩A) U (E’∩A)] A = P (E∩A) + E∩A E’ ∩ A P (E’∩A) = P(E) P(AE) + P(E’) P(AE’) E’

Misalkan kejadian merupakan suatu sekatan (partisi) dari ruang sampel T dengan P(Bi) ≠ 0 untuk i = 1, 2, …, k, Maka untuk setiap kejadian A, anggota T k k P(A) = ∑ P(Bi∩A) = ∑ P(Bi) P(ABi) I=1

Misalkan kejadian B 1, B 2, … Bk merupakan suatu sekatan (partisi) dari ruang sampel T dengan P(Bi) ≠ 0 untuk i = 1, 2, …, k, Misalkan A suatu kejadian sembarang dalam T dengan maka untuk r = 1, 2, …. , k

Tiga anggota koperasi dicalonkan menjadi ketua. Peluang Ali terpilih 0, 3, peluang Badu terpilih 0, 5, sedangkan peluang Cokro 0, 2. Kalau Ali terpilih maka peluang kenaikan iuran koperasi adalah 0, 8. Bila Badu atau Cokro yang terpilih maka peluang kenaikan iuran adalah masing-masing 0, 1 dan 0, 4. Bila seseorang merencanakan masuk jadi anggota koperasi tersebut tapi menundanya beberapa minggu dan kemudian mengetahui bahwa iuran telah naik, berapakah peluang Cokro terpilih jadi ketua?

Kejadian: A : Orang yang terpilih menaikkan iuran : Ali yang terpilih : Badu yang terpilih : Cokro yang terpilih