Respuesta en Frecuencia Circuitos Elctricos 2 Resonancia en

Respuesta en Frecuencia Circuitos Eléctricos 2

Resonancia en paralelo La resonancia es la condición que existe en todo sistema físico cuando una excitación senoidal de amplitud constante produce una respuesta máxima. Para una red eléctrica la resonancia es la condición que existe cuando la impedancia de entrada de la red es puramente resistiva. Una red está en resonancia cuando el voltaje y la corriente de las terminales de entrada se encuentran en fase.

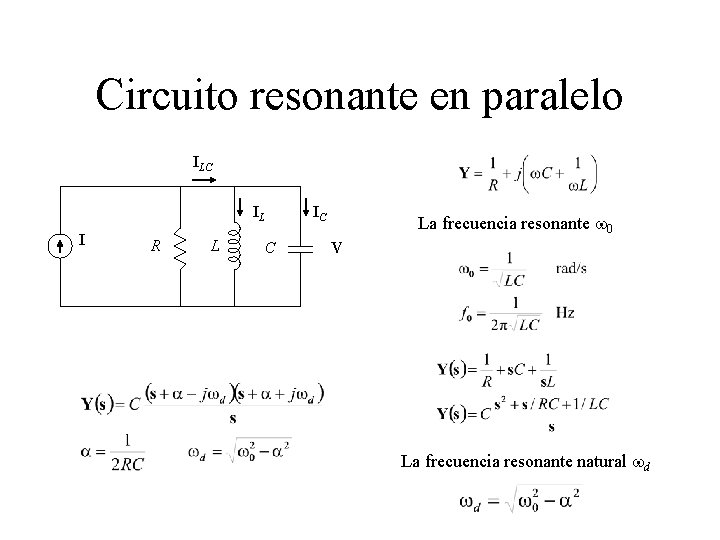
Circuito resonante en paralelo ILC IL I R L C IC La frecuencia resonante w 0 V La frecuencia resonante natural wd

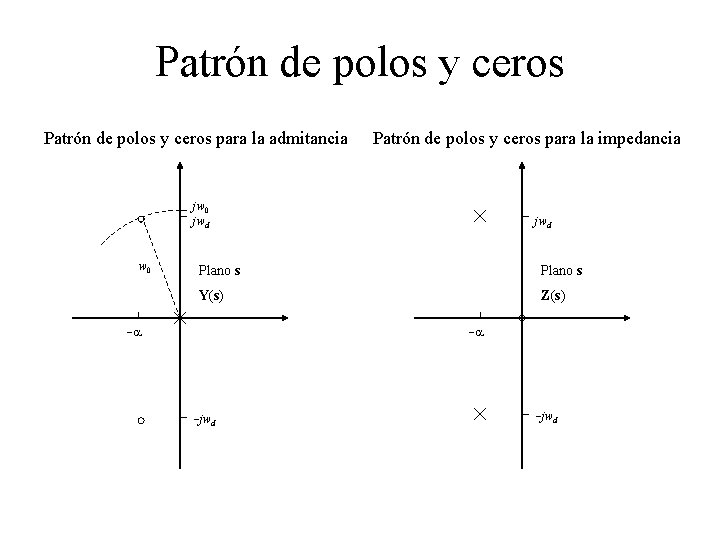
Patrón de polos y ceros para la admitancia Patrón de polos y ceros para la impedancia jw 0 jwd Plano s Y(s) Z(s) -a -a -jwd

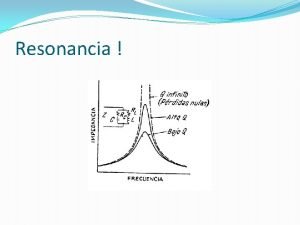
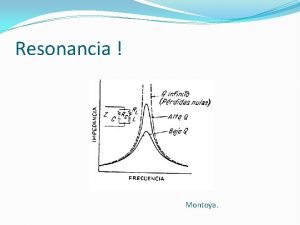
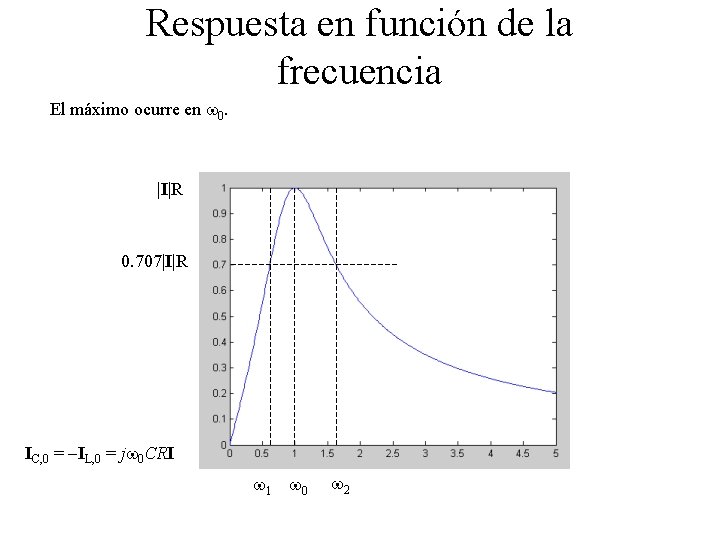
Respuesta en función de la frecuencia El máximo ocurre en w 0. |I|R 0. 707|I|R IC, 0 = -IL, 0 = jw 0 CRI w 1 w 0 w 2

Factor de calidad Q Q = factor de Calidad = 2 p Máxima energía almacenada Energía total perdida por ciclo

Otras relaciones Relaciones entre Q 0, a y wd Entonces Donde z es el factor de amortiguamiento

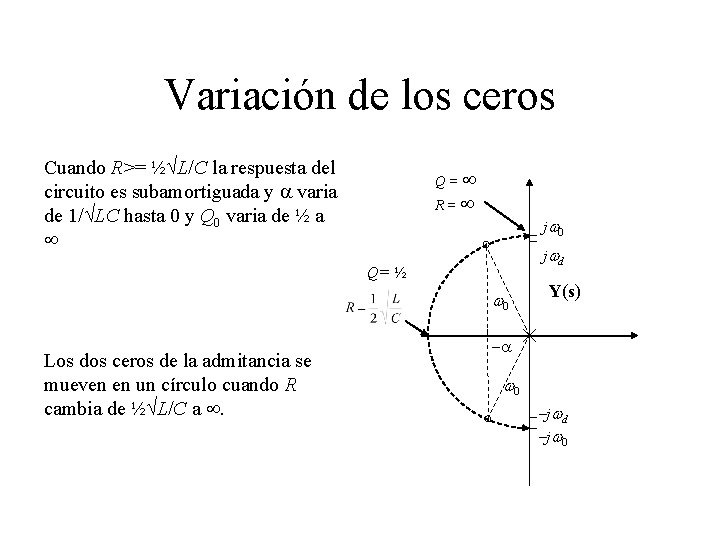
Variación de los ceros Cuando R>= ½ L/C la respuesta del circuito es subamortiguada y a varia de 1/ LC hasta 0 y Q 0 varia de ½ a Q= R= j w 0 j wd Q= ½ w 0 Los dos ceros de la admitancia se mueven en un círculo cuando R cambia de ½ L/C a . Y(s) -a w 0 - j wd - j w 0

Ancho de banda El ancho de banda (de media potencia) de un circuito resonante se define como la diferencia de dos frecuencias de media potencia. Si w 1 es la frecuencia inferior de mitad de potencia y w 2 es la frecuencia superior de mitad de potencia, entonces Los valores los encontramos cuando el voltaje vale 0. 707 de su valor máximo. Expresemos ahora el ancho de banda en términos de Q 0 y de la frecuencia resonante

La admitancia de circuito RLC en paralelo en términos de Q 0 o Para que la magnitud de Y sea 2/R, debemos obtener las frecuencias en las que la parte imaginaria tenga magnitud igual a 1. Al resolver tenemos

La diferencia entre estas expresiones proporciona una formula muy simple para el ancho de banda Los circuitos con Q 0 mas alta presentan un ancho de banda mas estrecho y tienen una selectividad de frecuencia o calidad superior. También se cumple

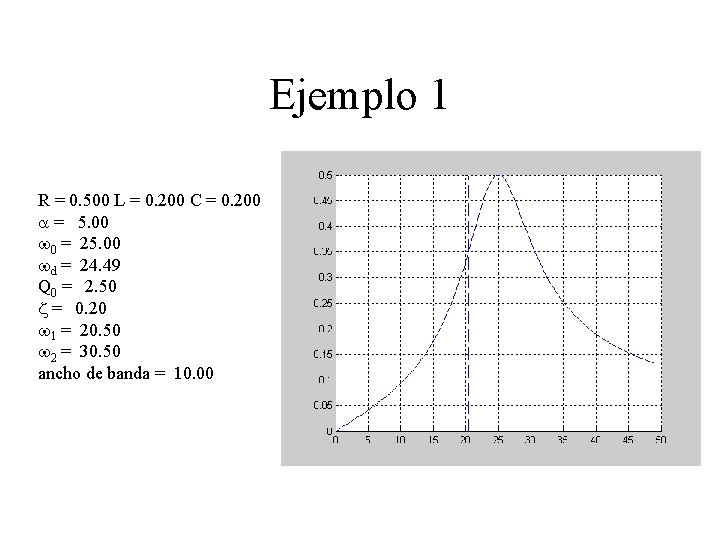
Ejemplo 1 R = 0. 500 L = 0. 200 C = 0. 200 a = 5. 00 w 0 = 25. 00 wd = 24. 49 Q 0 = 2. 50 z = 0. 20 w 1 = 20. 50 w 2 = 30. 50 ancho de banda = 10. 00

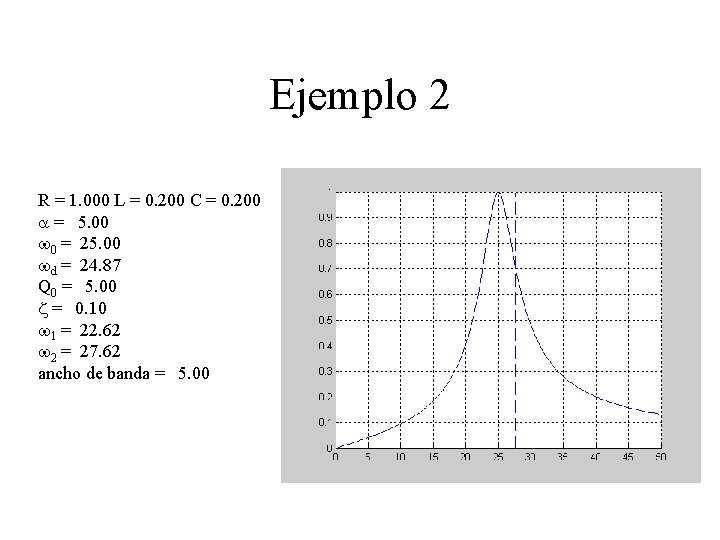
Ejemplo 2 R = 1. 000 L = 0. 200 C = 0. 200 a = 5. 00 w 0 = 25. 00 wd = 24. 87 Q 0 = 5. 00 z = 0. 10 w 1 = 22. 62 w 2 = 27. 62 ancho de banda = 5. 00

Aproximaciones para circuitos de alta Q Un circuito de alta Q es un circuito en el cual Q 0 es igual o mayor que 5 Dado que Entonces: Y las ubicaciones de los ceros se podrían aproximar por

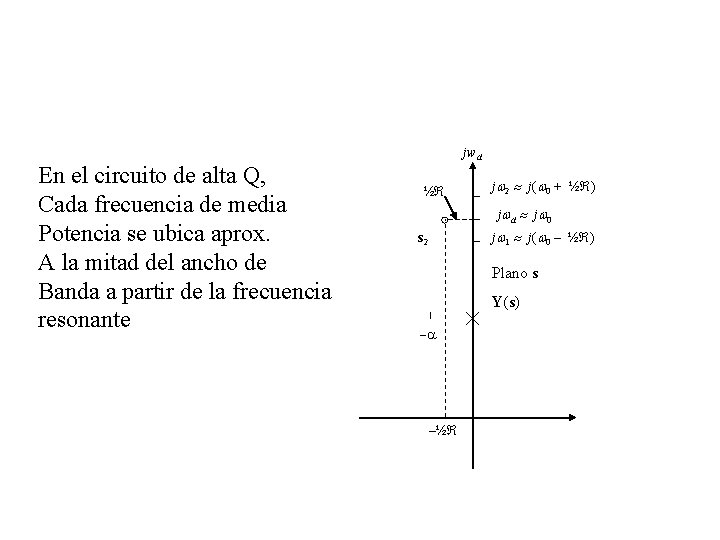
En el circuito de alta Q, Cada frecuencia de media Potencia se ubica aprox. A la mitad del ancho de Banda a partir de la frecuencia resonante jwd ½ jw 2 j(w 0 + ½ ) j wd j w 0 jw 1 j(w 0 – ½ ) s 2 Plano s Y(s) -a –½

Las ubicaciones de las dos frecuencias de media potencia también se pueden aproximar o s = jw s – s 2 La admitancia esta dada de manera aproximada por s = jw 0 s 2 ½

Sustituyendo La parte imaginaria de esta ecuación vendría siendo el numero de mitades de ancho de banda de resonancia y se abreviaría por medio de N, quedando así: donde

La magnitud de la admitancia es Y el ángulo estará dado por la tangente inversa

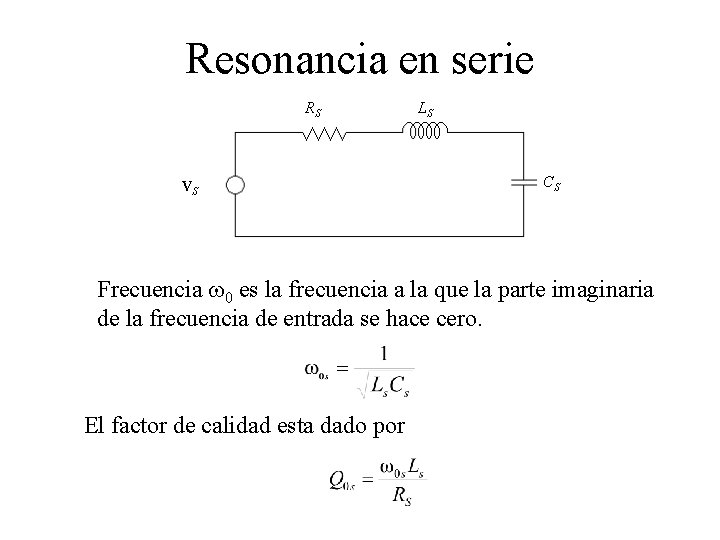
Resonancia en serie RS VS LS CS Frecuencia w 0 es la frecuencia a la que la parte imaginaria de la frecuencia de entrada se hace cero. El factor de calidad esta dado por

Resonancia en serie Las dos frecuencia w 1 s y w 2 s se definen como las frecuencias a las cuales la magnitud de la impedancia es 2 la magnitud mínima de la impedancia. Estas también son las frecuencias a las cuales la respuesta de corriente es igual al 70. 7 % de la respuesta máxima. Donde es la diferencia entre la frecuencia superior e inferior de la mitad de potencia. Este ancho de banda de la mitad de potencia esta dado por

Resonancia en serie La impedancia de entrada también puede expresarse en forma aproximada para circuitos con valores altos de Qs. Donde El circuito resonante en serie se caracteriza por una baja impedancia resonante

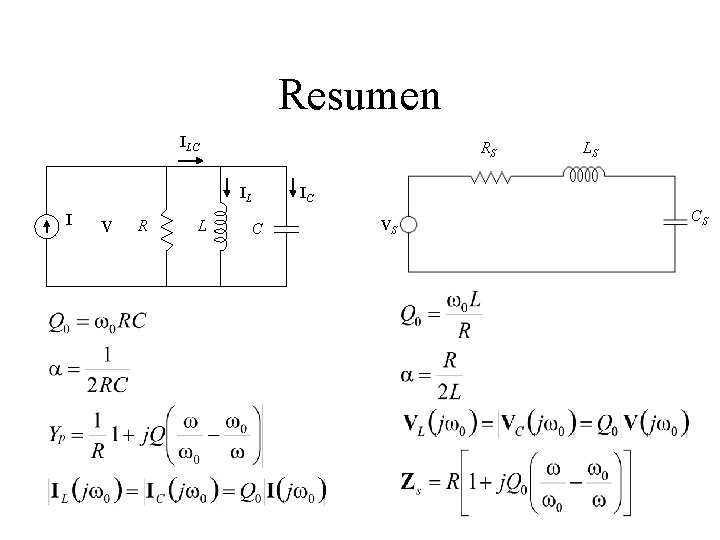
Resumen ILC RS IL I V R L C LS IC VS CS

Tabla de expresiones Expresiones exactas Expresiones aproximadas Q 0 >=5 wd = w 0 0. 9 w 0<= |w| <=1. 1 w 0 w 2, 1 = w 0 ½

Tarea Un circuito resonante serie tiene un ancho de banda de 100 Hz y contiene una inductancia de 20 m. H y una capacitancia de 2 m. F. Determine a) f 0, b) Q 0, c) Zent y d) f 2. 796 Hz, 7. 96, 12. 57 + 0 j Omhs, 846 Hz

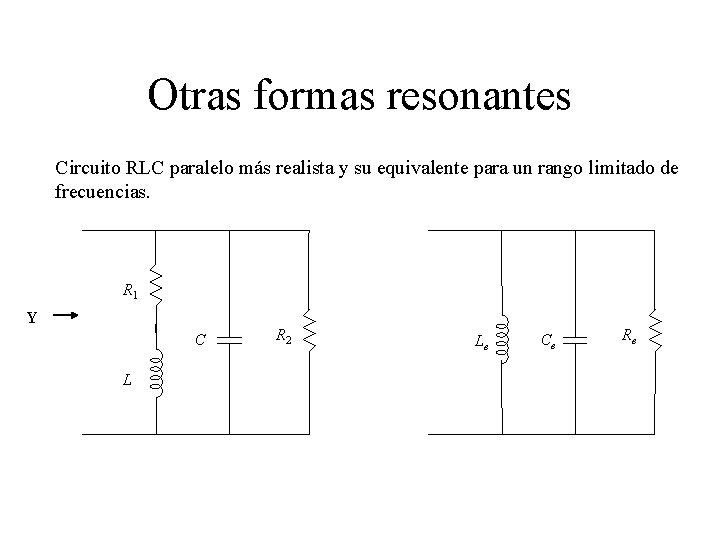
Otras formas resonantes Circuito RLC paralelo más realista y su equivalente para un rango limitado de frecuencias. R 1 Y C L R 2 Le Ce Re

La frecuencia angular resonante se encuentra haciendo cero: Resolviendo, obtenemos

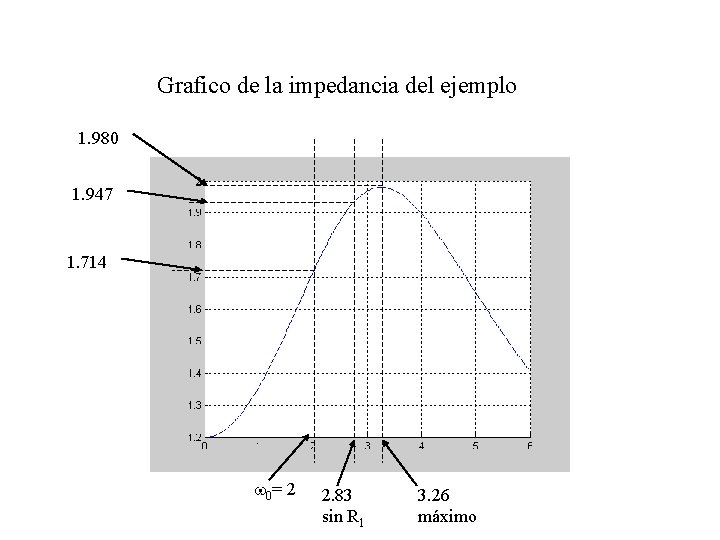
Ejemplo Sean R 1 = 2 Ohms, L = 1 H, C = 1/8 F y R 2 = 3 Ohms. w 0 = 8 – 22 = 2 rad/s Y = 1/3 + j 2(1/8) + 1/(2 + j(2)(1)) = 1/3 + 1/4 = 0. 583 S Z(2 j) = 1/0. 583 = 1. 714 Ohms Si R 1 fuera cero w 0 = 2. 83 rad/s Z(2. 83 j) = 1. 947/_-13. 26° Ohms Frecuencia del máximo wm = 3. 26 rad/s Z(3. 26 j) = 1. 980/_-21. 4° Ohms

Grafico de la impedancia del ejemplo 1. 980 1. 947 1. 714 w 0 = 2 2. 83 sin R 1 3. 26 máximo

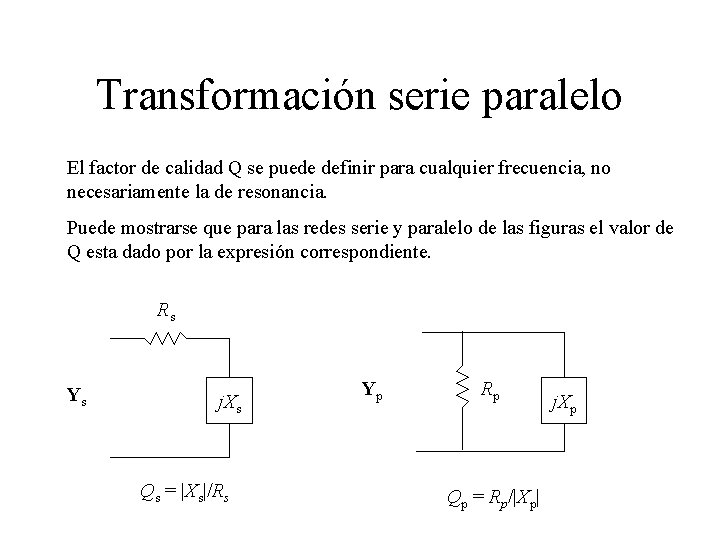
Transformación serie paralelo El factor de calidad Q se puede definir para cualquier frecuencia, no necesariamente la de resonancia. Puede mostrarse que para las redes serie y paralelo de las figuras el valor de Q esta dado por la expresión correspondiente. Rs Ys j. Xs Qs = |Xs|/Rs Yp Rp Qp = Rp/|Xp| j. Xp

Para que las dos redes sean equivalentes se debe cumplir lo siguiente Esto se cumple si Dividiendo ambas Las Q’s de las dos redes deben ser iguales Qs = Qp = Q, por tanto

Ejemplo En w = 1000 rad/s, encuentre la red paralela equivalente a la red serie 100 Ohms 8 H Rp = 100 (1 + (8*1000)2/1002) = 640 k. Ohms Xp = 8*1000(1 + 1/ ((8*1000)2/1002)) = 8000 = 1000*Lp Lp = 8 H

Ejemplo 2 Suponga una red serie RLC con R = 20 , L = 10 m. H y C = 0. 01 m. F. La red es exitada por una fuente de 0. 5 V y se desea medir el voltaje en el capacitor con un voltímetro con 100000 de resistencia interna. Antes de conectar w 0 = 105 rad/s, Q 0 = 50 y VC = 25 V. El arreglo del capacitor en paralelo con la resistencia del voltímetro es equivalente a un arreglo serie de un capacitor y una resistencia. Para calcular los valores del circuito equivalente se debe suponer que la frecuencia de resonancia es también de 105 rad/s, la Q de la red RC estará dada por Q = Rp/|Xp| = w. RC = 100 Los elementos equivalentes son Cs = Cp y Rs = Rp/Q = 10 La nueva Q del circuito RLC es 33. 3. El voltaje en el arreglo serie es |VC| = (0. 5/30)|10 – j 1000| = 16. 67 V

Tarea Dados una resistencia de 10 en serie con un condensador de 10 m. F, determinar los dos elementos en el equivalente en paralelo si w = : a) 200, b) 1000, c) 5000 rads/s. Resp. : 50 , 8 m. F; 1 k , 10 m. F; 25 k , 10 m. F Para w = 105 rads/s, hallar el valor eficaz de Q para las redes RC de dos terminales que se muestran en las figuras +---+ | | R 1 C | | +---+ +---R 2 ---+ | | R 1 C | | +----+---+ +---R 2 ---+ | | | R 3 R 1 C | | | +--------+ R 1 = 4 k , R 2 = 10 , R 3 = 500 , C = 5 m. F Resp. : 2, 10, 20

Cambio de Escala El Procedimiento de cambio de escala nos permite analizar redes formadas por elementos con valores prácticos haciendo un cambio de escala para permitir cálculos numéricos mas convenientes, tanto en magnitud como en frecuencia.

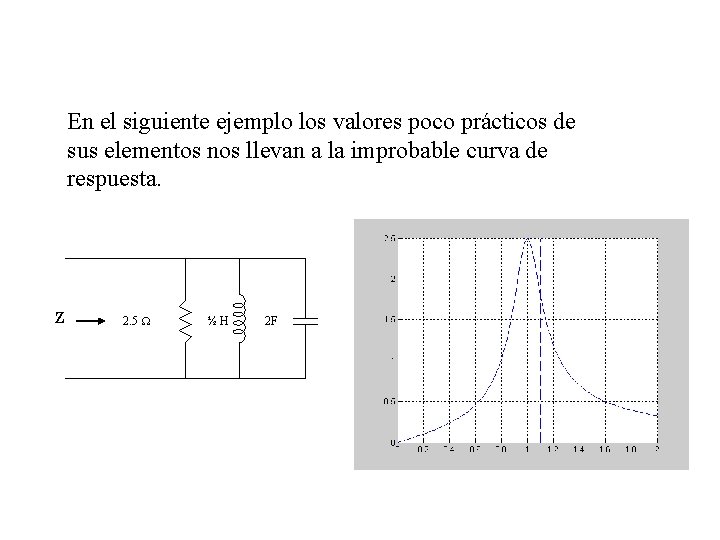
En el siguiente ejemplo los valores poco prácticos de sus elementos nos llevan a la improbable curva de respuesta. Z 2. 5 ½H 2 F

Cambio de Escala El cambio de escala en magnitud: se define como el proceso por medio del cual la impedancia de una red de dos terminales aumenta por un factor de Km y la frecuencia permanece constante.

Cambio de Escala en Magnitud Por consiguiente “la red sufrira un cambio de escala en magnitud por un factor de 2”, esto significa que la impedancia de la nueva red sera el doble de la red original: Los siguientes cambios darán como resultado la red con otra escala en magnitud por el factor Km : R Km R L Km L C Cambio de escala en magnitud

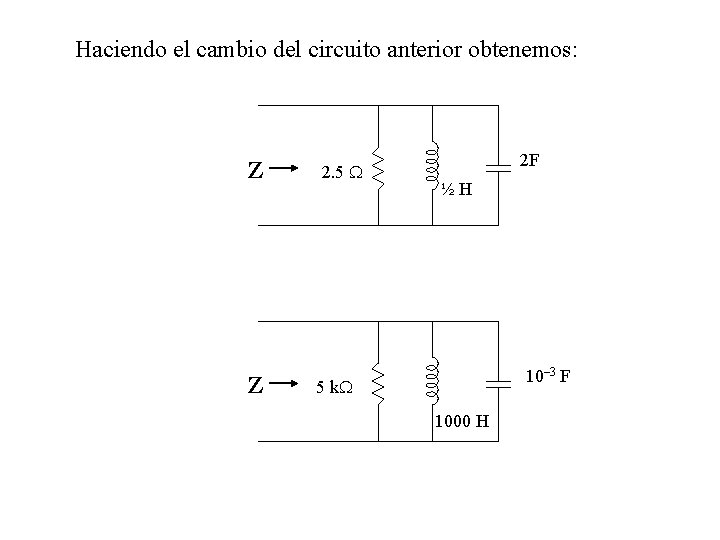
Haciendo el cambio del circuito anterior obtenemos: Z Z 2. 5 2 F ½H 10– 3 F 5 k 1000 H

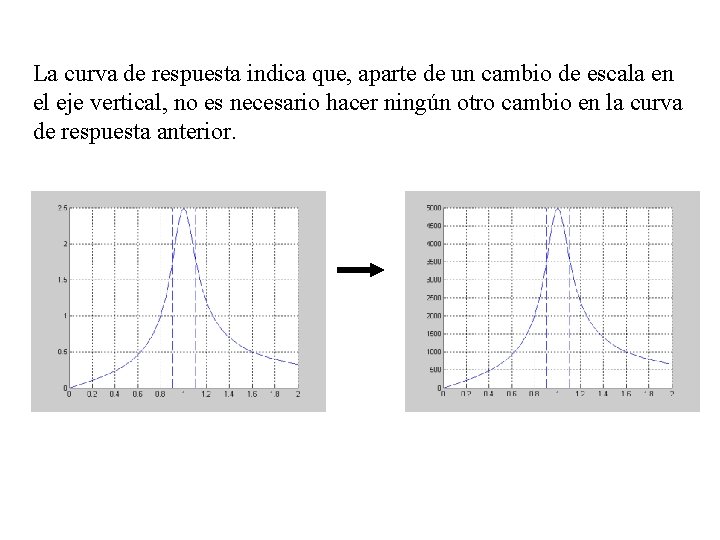
La curva de respuesta indica que, aparte de un cambio de escala en el eje vertical, no es necesario hacer ningún otro cambio en la curva de respuesta anterior.

Cambio de Escala en Frecuencia El cambio de escala en frecuencia se define como el proceso por medio del cual la frecuencia a la que ocurre cualquier impedancia aumenta por un factor Kf Al igual que en el caso anterior “la red sufre un cambio de escala en frecuencia por un factor de 2”. El cambio de escala se logra cambiando la escala en frecuencia de cada elemento pasivo.

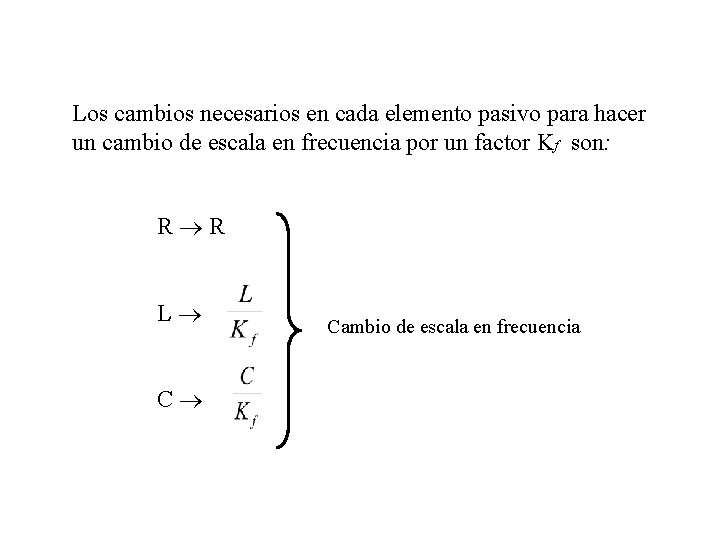
Los cambios necesarios en cada elemento pasivo para hacer un cambio de escala en frecuencia por un factor Kf son: R R L C Cambio de escala en frecuencia

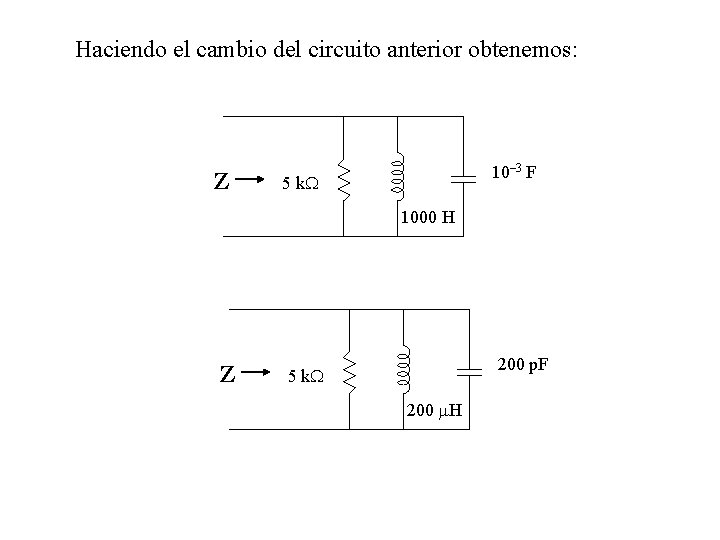
Haciendo el cambio del circuito anterior obtenemos: Z 10– 3 F 5 k 1000 H Z 200 p. F 5 k 200 m. H

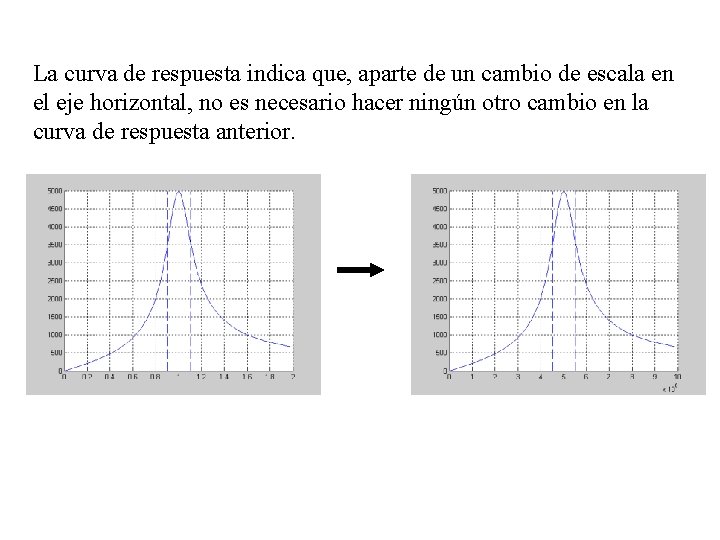
La curva de respuesta indica que, aparte de un cambio de escala en el eje horizontal, no es necesario hacer ningún otro cambio en la curva de respuesta anterior.

Una impedancia dada como función de s también puede cambiar su escala, sea en magnitud o en frecuencia. Para un cambio de escala en magnitud de Z(s): solo multiplicamos Z(s) por el factor Km. Ejemplo: La impedancia Z´(s) de la red con cambio de escala en magnitud es: Z´(s)=Km Z(s)

Para el cambio de escala en frecuencia: Z´´(s)=Z´ Siempre y cuando Z´´(s) y Z´(s) deben dar valores idénticos de impedancia Estos dos tipos de cambios de escala también pueden ser realizados a las fuentes dependientes

Tarea Un circuito resonante en paralelo tiene una frecuencia de resonancia 2500 rad/s, un ancho de banda de 100 rad/s y una inductancia de 200 m. H. Halle el nuevo ancho de banda y capacitancia si se emplea una escala en el circuito en a) la magnitud por un factor de 5; b) la frecuencia por un factor de 5; c) magnitud y la frecuencia por factores de 5. Una tensión V(s) aplicada a una red dada produce una salida I 2(s) = (2 s+5)/(3 s 2 + 4 s+ 6)A. Hallar I 2(s) si la red tiene una escala en a) frecuencia por un factor de 2; b) magnitud por un factor de 2; c) frecuencia y magnitud por factores de 2; b)

Diagramas de Bode Definición: Una magnitud en decibeles se obtiene tomando el logaritmo en base 10 de la magnitud y multiplicando por 20. Hd. B = 20 log|H(jw)| La operación inversa es: |H(jw)| = 10(H /20) d. B Algunos valores comunes son: |H(jw)| = 1 Hd. B = 0 d. B |H(jw)| = 2 Hd. B = 6 d. B |H(jw)| = 10 Hd. B = 20 d. B |H(jw)| = 10 n Hd. B = 20 n d. B 20 log 5 = 20 log(10/2) = 20 log 10 – 20 log 2 = 20 – 6 = 14 d. B 2 20 log 21/2 = 10 x 0. 3 = 3 d. B 1/ 2 -3 d. B

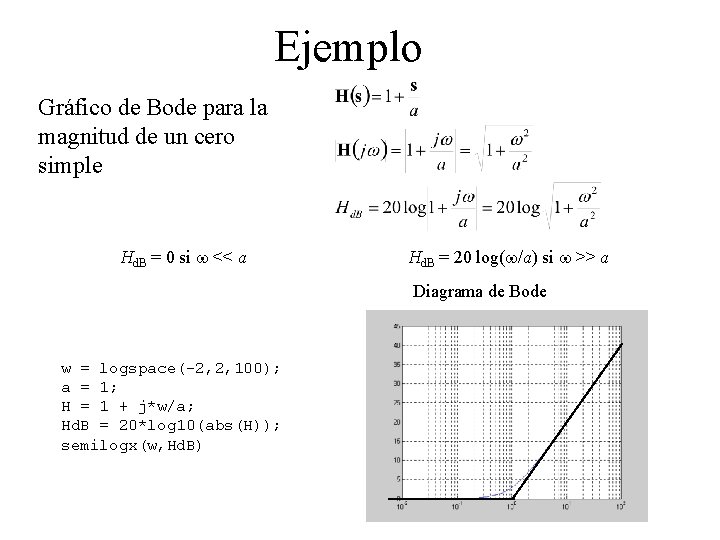
Ejemplo Gráfico de Bode para la magnitud de un cero simple Hd. B = 0 si w << a Hd. B = 20 log(w/a) si w >> a Diagrama de Bode w = logspace(-2, 2, 100); a = 1; H = 1 + j*w/a; Hd. B = 20*log 10(abs(H)); semilogx(w, Hd. B)

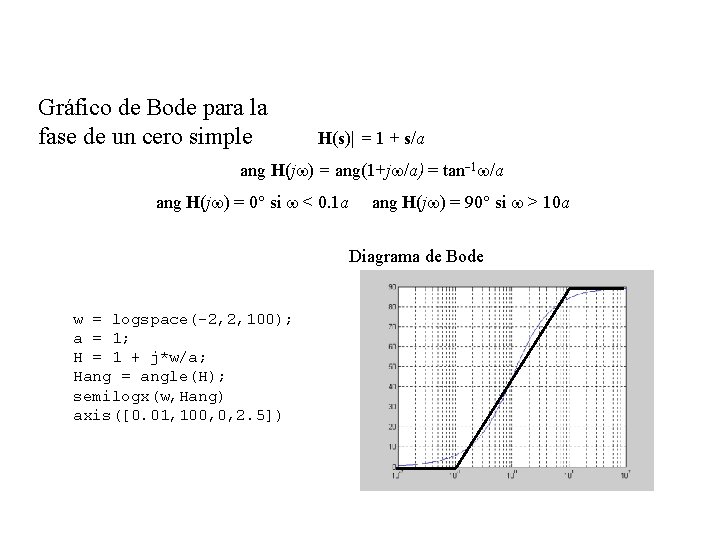
Gráfico de Bode para la fase de un cero simple H(s)| = 1 + s/a ang H(jw) = ang(1+jw/a) = tan-1 w/a ang H(jw) = 0° si w < 0. 1 a ang H(jw) = 90° si w > 10 a Diagrama de Bode w = logspace(-2, 2, 100); a = 1; H = 1 + j*w/a; Hang = angle(H); semilogx(w, Hang) axis([0. 01, 100, 0, 2. 5])

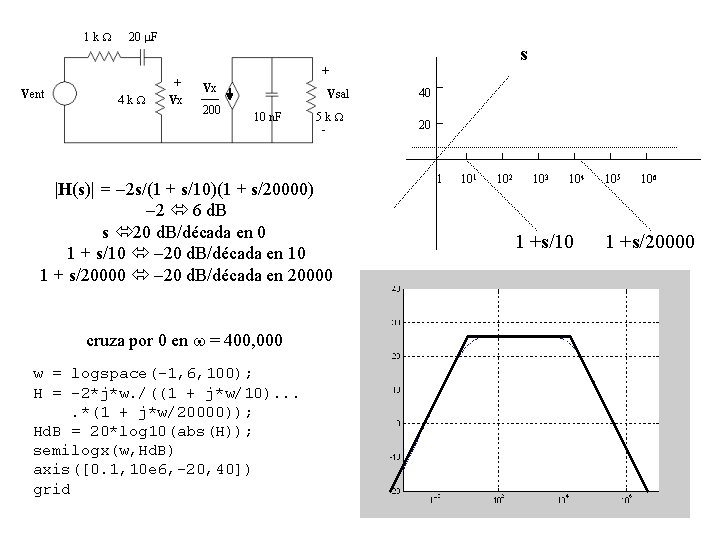
1 k Vent 20 m. F 4 k s + Vx 200 Vsal 10 n. F 5 k - |H(s)| = -2 s/(1 + s/10)(1 + s/20000) -2 6 d. B s 20 d. B/década en 0 1 + s/10 -20 d. B/década en 10 1 + s/20000 -20 d. B/década en 20000 cruza por 0 en w = 400, 000 w = logspace(-1, 6, 100); H = -2*j*w. /((1 + j*w/10). . *(1 + j*w/20000)); Hd. B = 20*log 10(abs(H)); semilogx(w, Hd. B) axis([0. 1, 10 e 6, -20, 40]) grid 40 20 1 102 103 104 1 +s/10 105 106 1 +s/20000

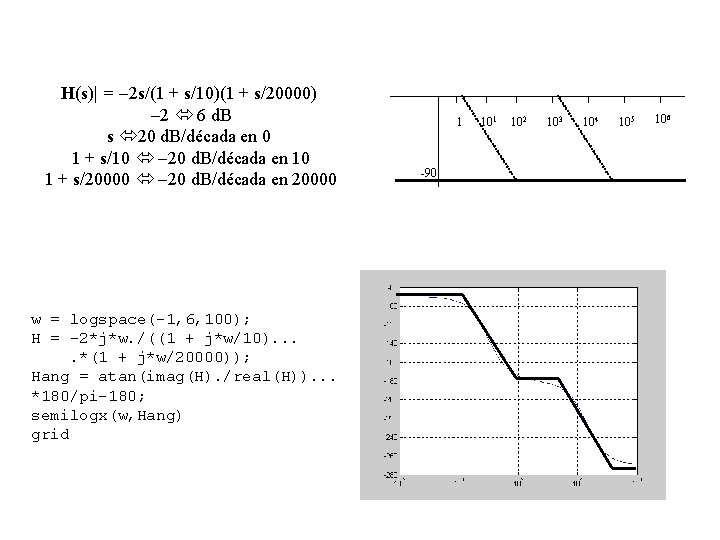
H(s)| = -2 s/(1 + s/10)(1 + s/20000) -2 6 d. B s 20 d. B/década en 0 1 + s/10 -20 d. B/década en 10 1 + s/20000 -20 d. B/década en 20000 w = logspace(-1, 6, 100); H = -2*j*w. /((1 + j*w/10). . *(1 + j*w/20000)); Hang = atan(imag(H). /real(H)). . . *180/pi-180; semilogx(w, Hang) grid 1 -90 101 102 103 104 105 106

Algunas consideraciones Un término s n representa una magnitud que pasa por w = 1, con una pendiente de 20 n d. B/década, la respuesta en fase es un ángulo constante de 90 n°. Un cero múltiple (1+ s/a)n representa la suma de n curvas de respuesta en magnitud o fase de un cero simple. Por tanto se obtiene una respuesta de 0 d. B para w<a y que tiene una pendiente de 20 n d. B/década cuando w>a. el error es – 3 n d. B en w=a, y –n d. B en 0. 5 a y 2 a. El diagrama de fase es 0° para w<0. 1 a, 90 n° para w>10 a, 45 n° para w=a, y una línea recta con pendiente de 45 n°/década para 0. 1 a<w<10 a. El error es 5. 71 n° en las dos frecuencias.

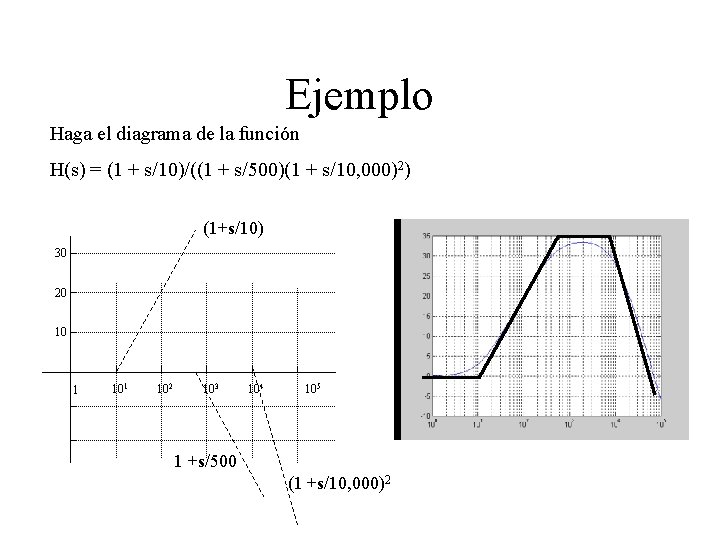
Ejemplo Haga el diagrama de la función H(s) = (1 + s/10)/((1 + s/500)(1 + s/10, 000)2) (1+s/10) 30 20 10 1 102 103 104 105 1 +s/500 (1 +s/10, 000)2

Pares complejos conjugados |H(s)| = 1 + 2 z(s/w 0) + (s/w 0) Hd. B = 20 log|H(s)| = 20 log|1 + j 2 z(w/w 0) - (w/w 0)2| Si z = 1 se tiene un cero de segundo orden. Se tiene una asíntota en 0 d. B y otra que corresponde al término cuadrático de – 40 d. B/década. Para w = w 0 hay que hacer un ajuste, Hd. B = 20 log(2 z) Si z = 0. 1, Hd. B = – 14 d. B. w = logspace(-2, 1, 100); w 0 = 1; zeta = 1; H 1 = 1 + 2*zeta*j*w/w 0 -. . . (w/w 0). ^2; Hd. B 1 = 20*log 10(abs(H 1)); z=1 z = 0. 5 z = 0. 25 z = 0. 1

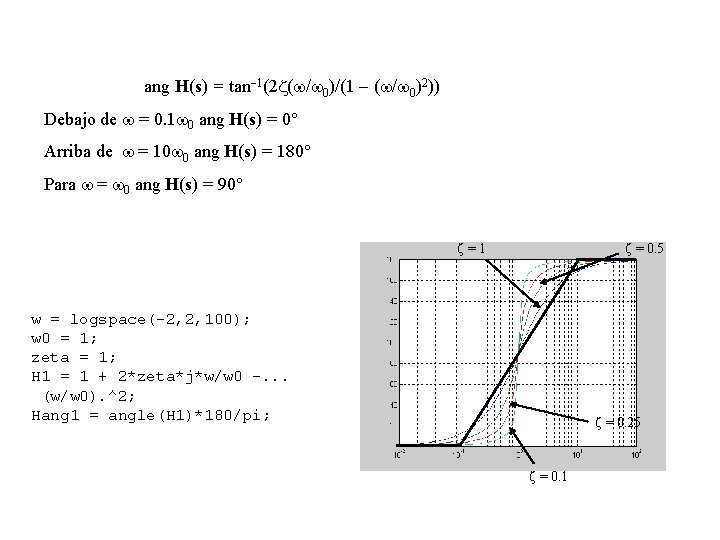
ang H(s) = tan-1(2 z(w/w 0)/(1 - (w/w 0)2)) Debajo de w = 0. 1 w 0 ang H(s) = 0° Arriba de w = 10 w 0 ang H(s) = 180° Para w = w 0 ang H(s) = 90° z=1 z = 0. 5 w = logspace(-2, 2, 100); w 0 = 1; zeta = 1; H 1 = 1 + 2*zeta*j*w/w 0 -. . . (w/w 0). ^2; Hang 1 = angle(H 1)*180/pi; z = 0. 25 z = 0. 1

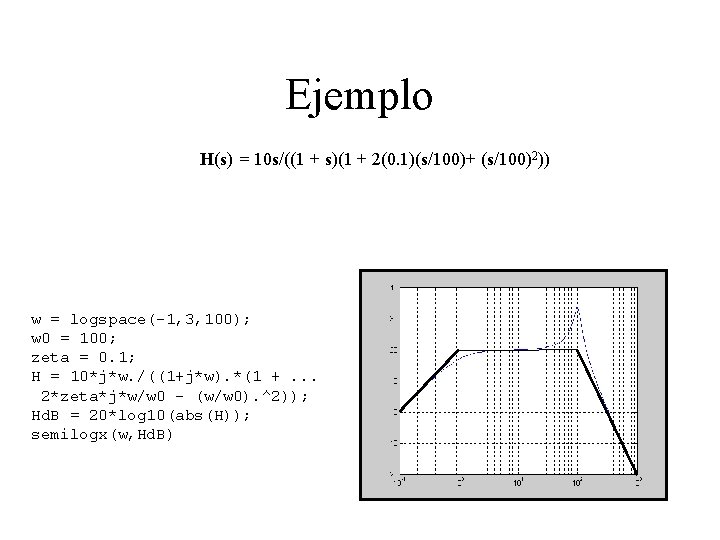
Ejemplo H(s) = 10 s/((1 + s)(1 + 2(0. 1)(s/100)+ (s/100)2)) w = logspace(-1, 3, 100); w 0 = 100; zeta = 0. 1; H = 10*j*w. /((1+j*w). *(1 +. . . 2*zeta*j*w/w 0 - (w/w 0). ^2)); Hd. B = 20*log 10(abs(H)); semilogx(w, Hd. B)

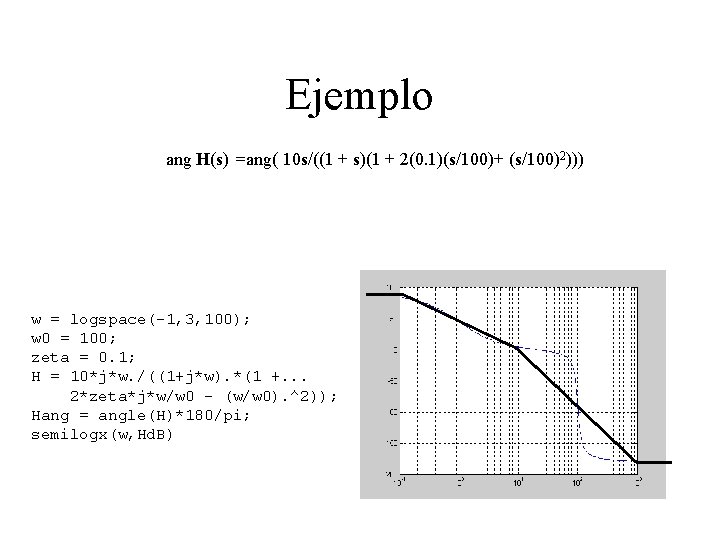
Ejemplo ang H(s) =ang( 10 s/((1 + s)(1 + 2(0. 1)(s/100)+ (s/100)2))) w = logspace(-1, 3, 100); w 0 = 100; zeta = 0. 1; H = 10*j*w. /((1+j*w). *(1 +. . . 2*zeta*j*w/w 0 - (w/w 0). ^2)); Hang = angle(H)*180/pi; semilogx(w, Hd. B)

Tarea Haga el diagrama de Bode de magnitud de H(s) = 1000 s 2/(s 2+5 s+100)