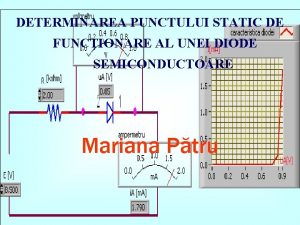
Regimurile fundamentale de funcionare ale S R A









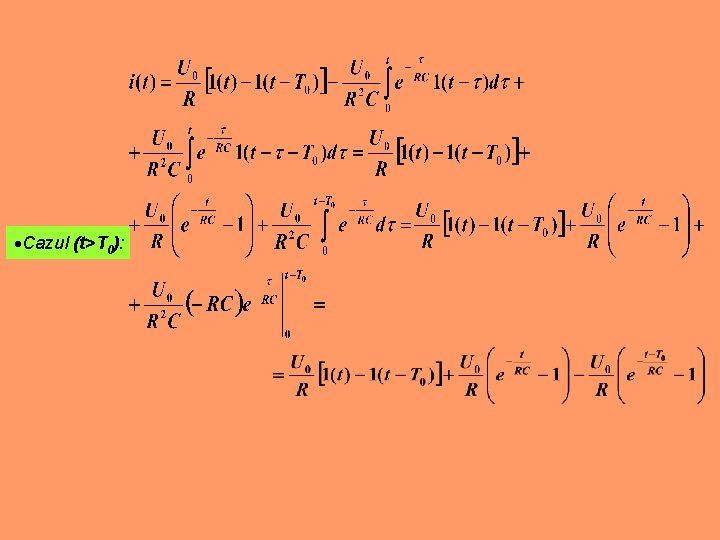


















- Slides: 46


Regimurile fundamentale de funcţionare ale S. R. A: Regimul de funcţionare a unui SRA se apreciază după forma variaţiei în timp a mărimii de ieşire y(t) (pentru y(t) se foloseşte deseori denumirea de răspuns al SRA). Regimul de funcţionare al unui SRA cuprins între două regimuri staţionare se numeşte regim dinamic sau regim tranzitoriu al sistemului de reglare automată. Mărimea de ieşire y(t) are o componentă forţată yf(t) şi o componentă liberă y (t), astfel că se poate scrie relaţia:

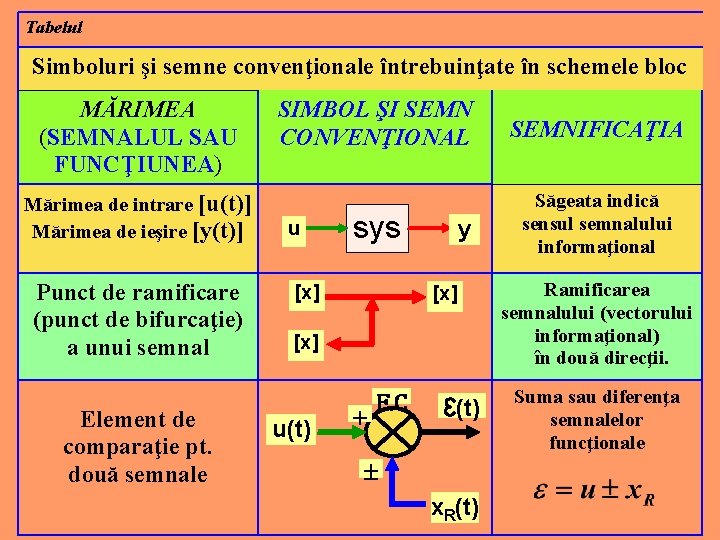
Tabelul Simboluri şi semne convenţionale întrebuinţate în schemele bloc MĂRIMEA (SEMNALUL SAU FUNCŢIUNEA) Mărimea de intrare [u(t)] Mărimea de ieşire [y(t)] Punct de ramificare (punct de bifurcaţie) a unui semnal Element de comparaţie pt. două semnale SIMBOL ŞI SEMN CONVENŢIONAL SEMNIFICAŢIA sys Săgeata indică sensul semnalului informaţional u [x] y [x] u(t) + E. C ℇ(t) ± x. R(t) Ramificarea semnalului (vectorului informaţional) în două direcţii. Suma sau diferenţa semnalelor funcţionale

Structura funcţională o reprezentare simbolică, (sau schema funcţională). Structura funcţională a unui sistem de reglare automată este acea schemă în care se indică elementele componente ale sistemului de reglare automată (SRA) destinaţia lor şi legăturile funcţionale între ele. Descrierea componenţei structurale SRA: Mărimile de timp u(t) - mărimea de intrare; y(t) - mărimea de ieşire; (t) - mărimea de eroare; x. R(t)- mărimea de reacţie; c(t) - mărimea de comandă; e(t) - mărimea de execuţie; Descriere blocuri E. C -element de comparaţie; R. A -regulator automat (sau algoritm de reglare); E. E - element de execuţie; I. A (I. T) - instalaţie tehnologică; E. M (T) - element de măsurare (traductor);

Problematizare S. R. A: Problema 1) Să se refacă topologia sistemului (formalismul intrare-ieşire) pentru toate ieşirile posibile netriviale? (nu se modifică dimensiunea sistemelor componente) Problema 2) Să se refacă topologia sistemului (formalismul intrare-ieşire) pentru toate intrările posibile netriviale? Problema 1) u sys Problema 2) y y 1=? y 2=? y 3=? y 4=? y 5=? =? u topologia SRA = ? u 1=? u 2=? u 3=? u 4=? sys y y 1=? y 2=? y 3=? y 4=? y 5=? =?

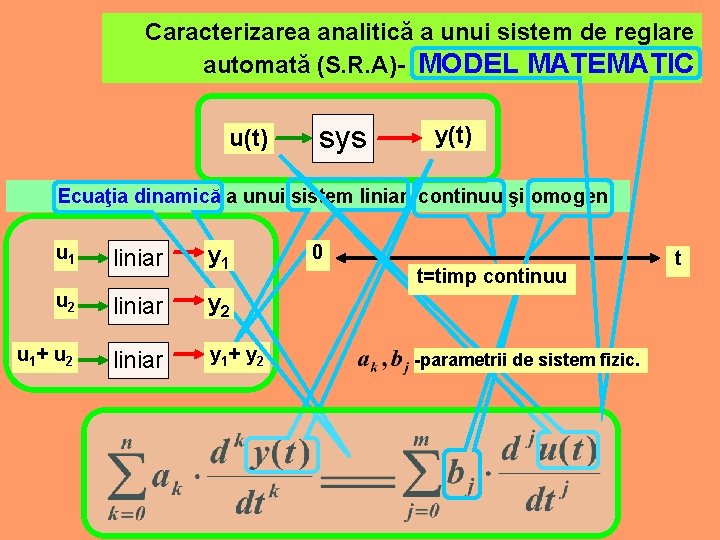
Caracterizarea analitică a unui sistem de reglare automată (S. R. A)- MODEL MATEMATIC u(t) sys y(t) Ecuaţia dinamică a unui sistem liniar, continuu şi omogen u 1 liniar y 1 u 2 liniar y 2 u 1 + u 2 liniar y 1 + y 2 0 t=timp continuu -parametrii de sistem fizic. t

OBS. Dacă prin transformări elementare obţinem combinaţii ale parametrilor de sistem fizic, numărul acestor parametri fiind egal cu - ordinul sistemului, atunci spunem că am obţinut cei parametrii de sistem. - ordinul sistemului - variabila independentă (timpul) - indicii de variaţie ai variaţilor succesive pentru mărimea de ieşire respectiv mărimea de intrare. relaţia de ordine care reprezintă condiţia de realizabilitate fizică a sistemului. condiţia sistemelor automate anticipative, (variaţii simultane succesive de acelaşi ordin pentru mărimea de ieşire, respectiv mărimea de intrare). condiţia sistemelor paranormale. OBS 1. Echilibrul asigurat de descrierea formală a ecuaţiei dinamice descrie o primă formă pt. modelul matematic al unui sistem automat (descris în timp continuu). 2. Ecuaţia dinamică se obţine dacă se realizează analiza fenomenologică a sistemului.

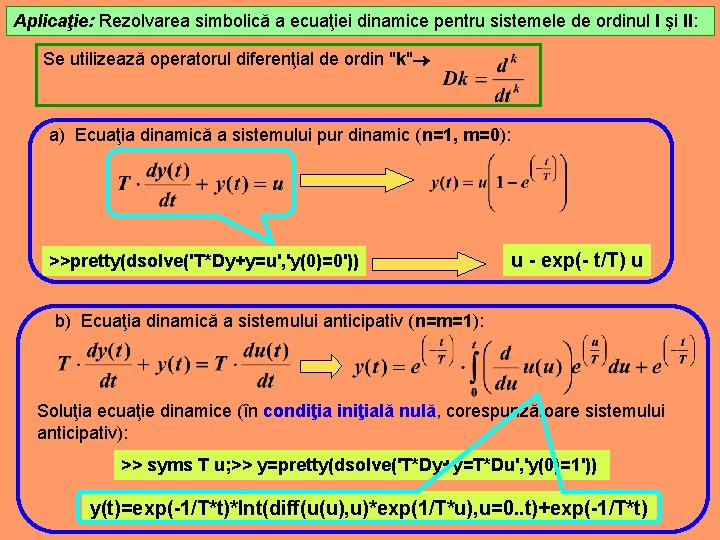
Aplicaţie: Rezolvarea simbolică a ecuaţiei dinamice pentru sistemele de ordinul I şi II: Se utilizează operatorul diferenţial de ordin "k" a) Ecuaţia dinamică a sistemului pur dinamic (n=1, m=0): >>pretty(dsolve('T*Dy+y=u', 'y(0)=0')) u - exp(- t/T) u b) Ecuaţia dinamică a sistemului anticipativ (n=m=1): Soluţia ecuaţie dinamice (în condiţia iniţială nulă, corespunzătoare sistemului anticipativ): >> syms T u; >> y=pretty(dsolve('T*Dy+y=T*Du', 'y(0)=1')) y(t)=exp(-1/T*t)*Int(diff(u(u), u)*exp(1/T*u), u=0. . t)+exp(-1/T*t)

c) Ecuaţia dinamică a sistemului pur dinamic de ordinul II (n=2, m=0): Soluţia ecuaţie dinamice (în condiţii iniţiale nule): >> syms a 2 a 1 a 0 b 0 u >> y=dsolve('a 2*D 2 y+a 1*Dy+a 0*y=b 0*u', 'y(0)=0', 'Dy(0)=0') y=1/a 0*b 0*u-1/2*b 0*u*(a 1+(a 1^2 -4*a 2*a 0)^(1/2))/(a 1^2 -4*a 2*a 0)^(1/2)/a 0*exp(1/2*(a 1 -(a 1^2 -4*a 2*a 0)^(1/2))*t/a 2)+1/2*b 0*u*(a 1 -(a 1^2 -4*a 2*a 0)^(1/2))/(a 1^24*a 2*a 0)^(1/2)/a 0*exp(-1/2*(a 1+(a 1^2 -4*a 2*a 0)^(1/2))*t/a 2

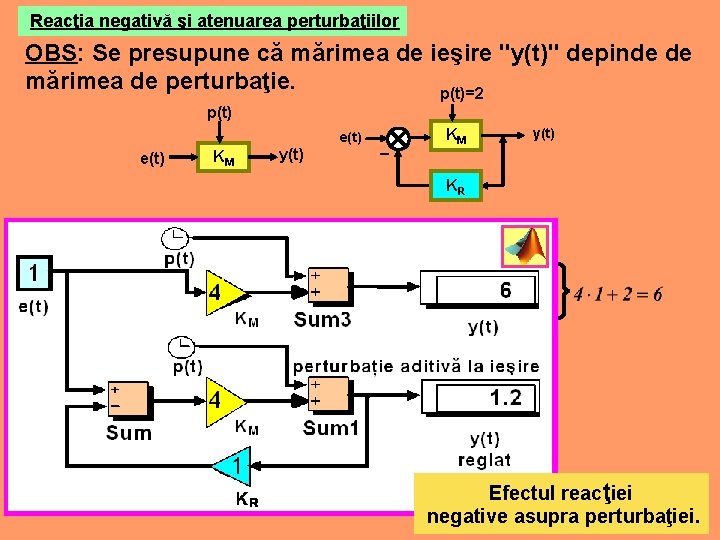
Reacţia negativă şi atenuarea perturbaţiilor OBS: Se presupune că mărimea de ieşire "y(t)" depinde de mărimea de perturbaţie. p(t)=2 p(t) e(t) KM y(t) – KM y(t) KR Efectul reacţiei negative asupra perturbaţiei.

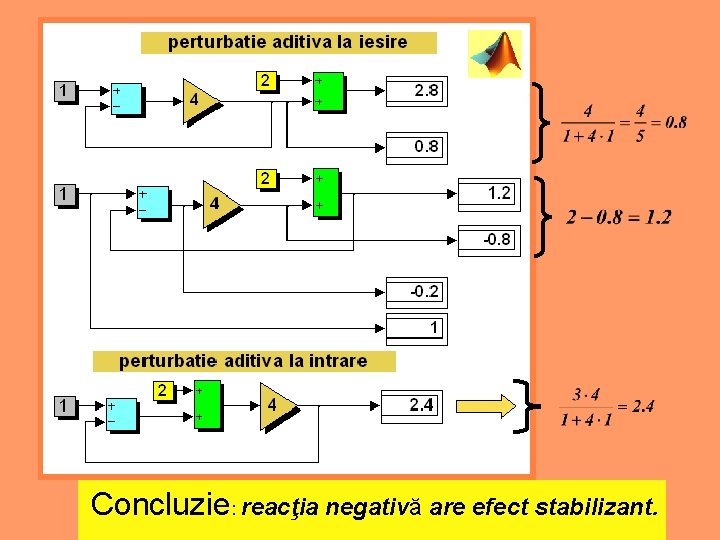
Concluzie: reacţia negativă are efect stabilizant.

1. Clasificarea sistemelor dinamice după structură: Prin structura fundamentală se înelege o reuniune de elemente ale cărei proprietăţi nu se regăsesc, ca atare, printre proprietăţile elementelor componente. Proprietăţile unei structuri fundamentale aparţin în primul rând conexiunilor dintre elementele componente (elemente de bază), respectiv reuniunii structurate a elementelor şi raporturilor dintre elementele de bază. Dupa prezenţa sau absenţa reacţiei se disting sisteme cu structură: deschisă respectiv închisă.

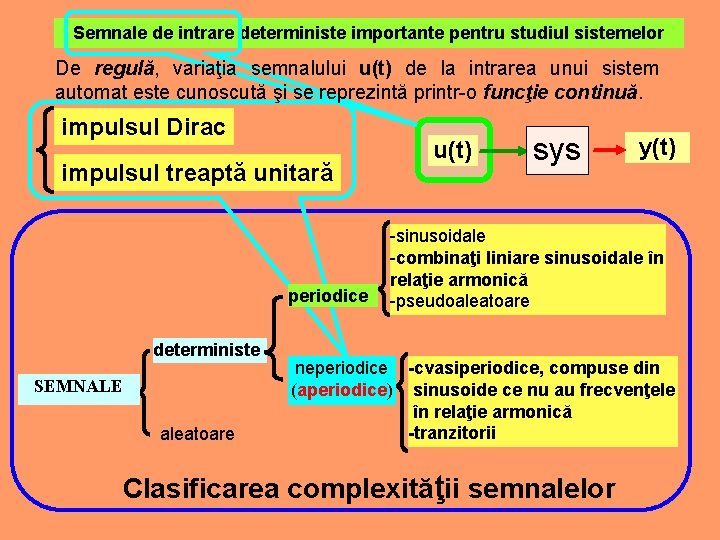
Semnale de intrare deterministe importante pentru studiul sistemelor De regulă, variaţia semnalului u(t) de la intrarea unui sistem automat este cunoscută şi se reprezintă printr-o funcţie continuă. impulsul Dirac impulsul treaptă unitară periodice deterministe SEMNALE aleatoare u(t) sys y(t) -sinusoidale -combinaţi liniare sinusoidale în relaţie armonică -pseudoaleatoare neperiodice -cvasiperiodice, compuse din (aperiodice) sinusoide ce nu au frecvenţele în relaţie armonică -tranzitorii Clasificarea complexităţii semnalelor

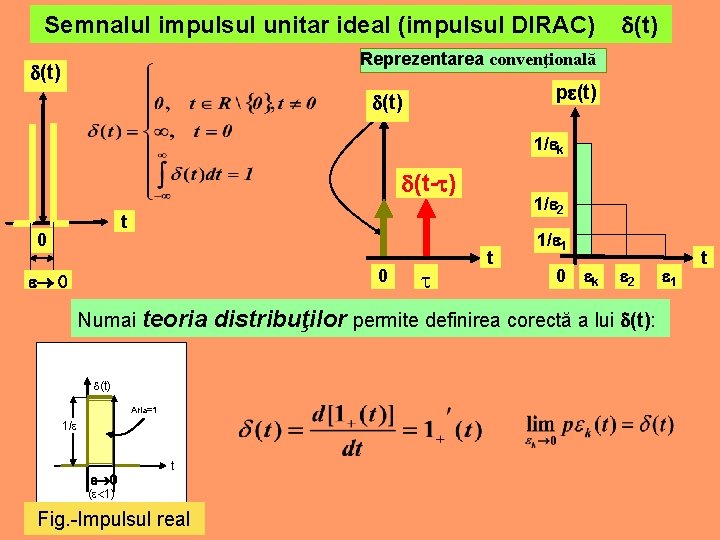
Semnalul impulsul unitar ideal (impulsul DIRAC) (t) Reprezentarea convenţională (t) p (t) 1/ k (t- ) 1/ 2 t 0 0 Numai teoria (t) Aria=1 1/ t ( 1) Fig. -Impulsul real t 1/ 1 0 k 2 distribuţilor permite definirea corectă a lui (t): 1 t

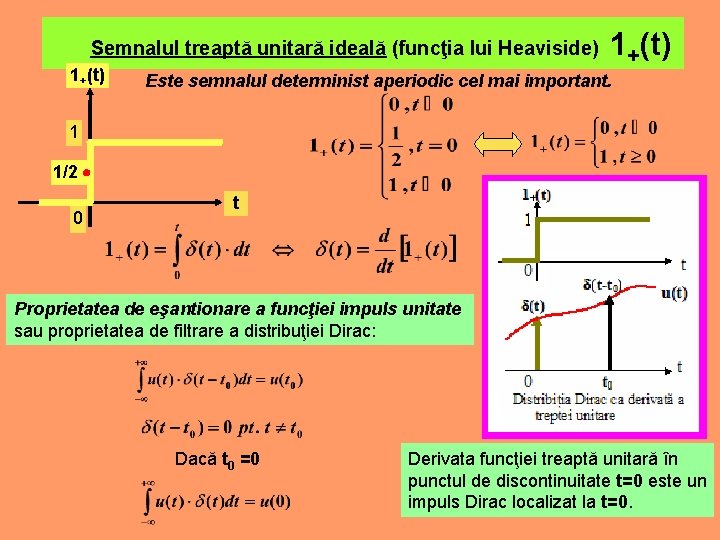
Semnalul treaptă unitară ideală (funcţia lui Heaviside) 1+(t) Este semnalul determinist aperiodic cel mai important. 1 1/2 0 t Proprietatea de eşantionare a funcţiei impuls unitate sau proprietatea de filtrare a distribuţiei Dirac: Dacă t 0 =0 Derivata funcţiei treaptă unitară în punctul de discontinuitate t=0 este un impuls Dirac localizat la t=0.

Proprietatea de sondare a funcţiei delta (t): Un semnal oarecare poate fi exprimat astfel: convoluţia cu (t): Descompunerea unei funcţii u(t) în integrală de funcţii treaptă unitate Descompunerea unei funcţii u(t) în integrală de distribuţii delta unitate. Deoarece t , pentru t , limita superioară a integralei este "t" şi cea inferioară este zero:

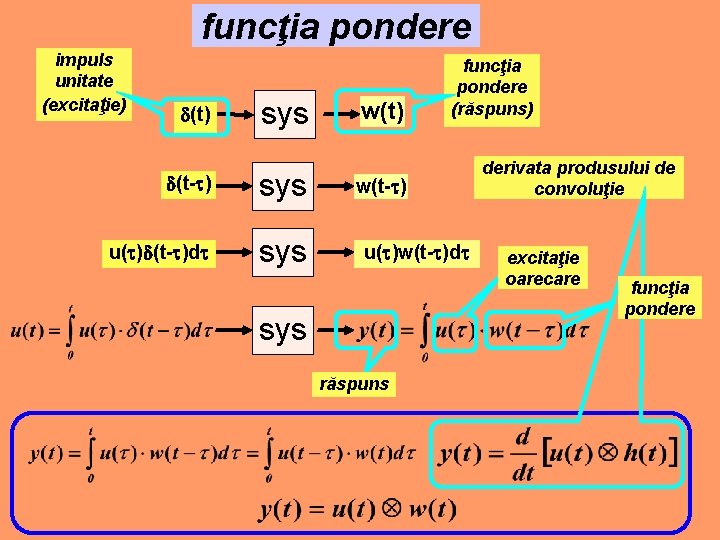
funcţia pondere impuls unitate (excitaţie) (t) sys (t- ) sys u( ) (t- )d sys w(t) funcţia pondere (răspuns) w(t- ) u( )w(t- )d sys răspuns derivata produsului de convoluţie excitaţie oarecare funcţia pondere

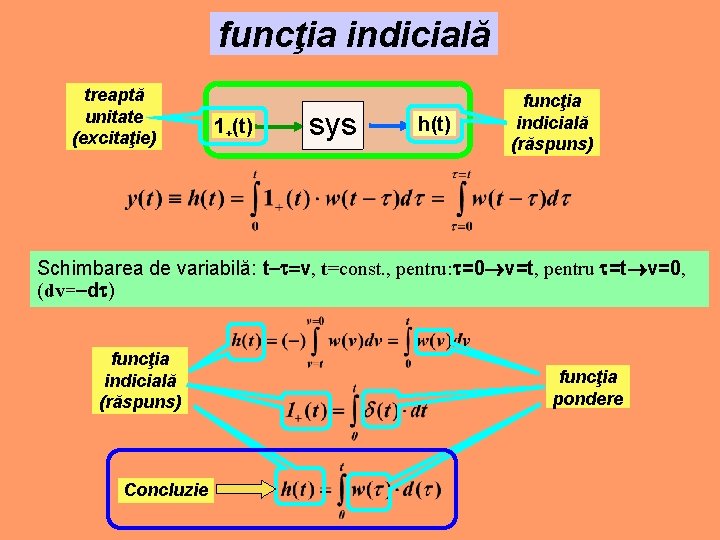
funcţia indicială treaptă unitate (excitaţie) 1+(t) sys h(t) funcţia indicială (răspuns) Schimbarea de variabilă: t v, t=const. , pentru: =0 v=t, pentru =t v=0, (dv= d ) funcţia indicială (răspuns) Concluzie funcţia pondere

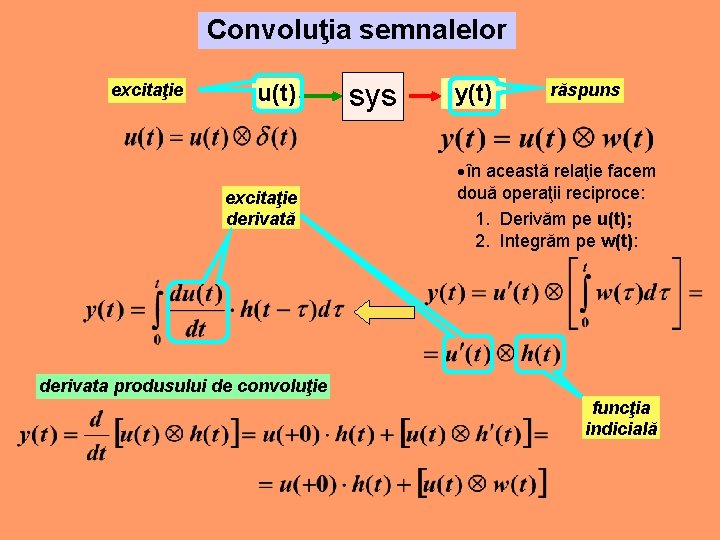
Convoluţia semnalelor excitaţie u(t) excitaţie derivată sys y(t) răspuns în această relaţie facem două operaţii reciproce: 1. Derivăm pe u(t); 2. Integrăm pe w(t): derivata produsului de convoluţie funcţia indicială

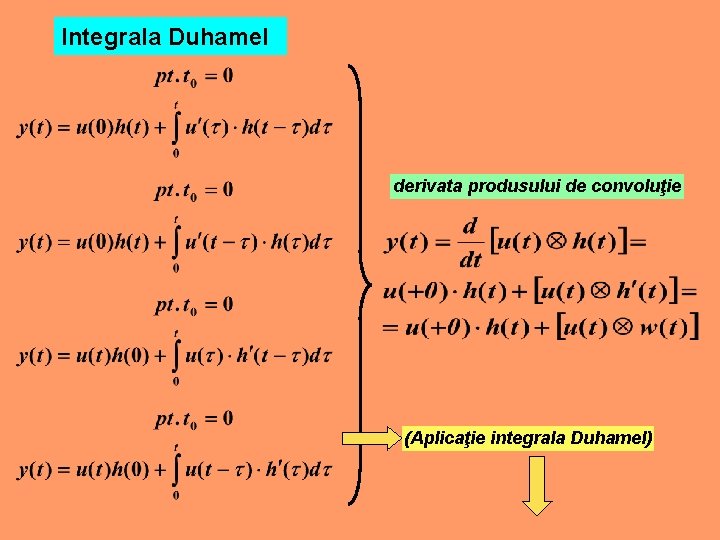
Integrala Duhamel derivata produsului de convoluţie (Aplicaţie integrala Duhamel)

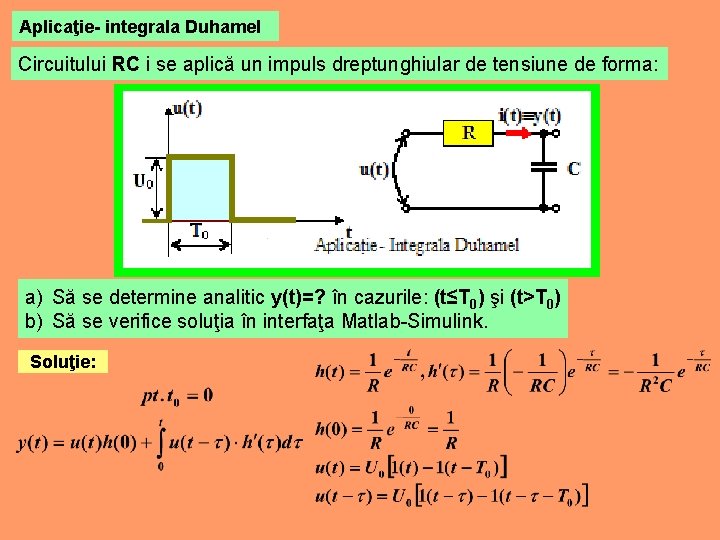
Aplicaţie- integrala Duhamel Circuitului RC i se aplică un impuls dreptunghiular de tensiune de forma: a) Să se determine analitic y(t)=? în cazurile: (t≤T 0) şi (t>T 0) b) Să se verifice soluţia în interfaţa Matlab-Simulink. Soluţie:

Cazul (t≤T 0):
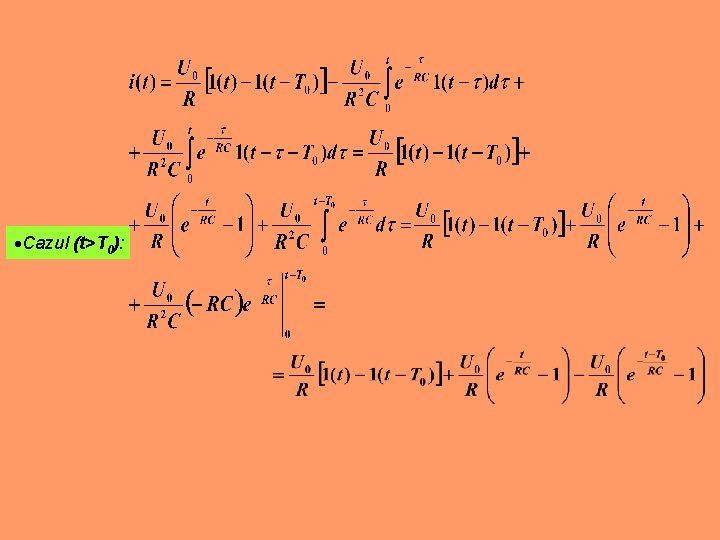
Cazul (t>T 0):

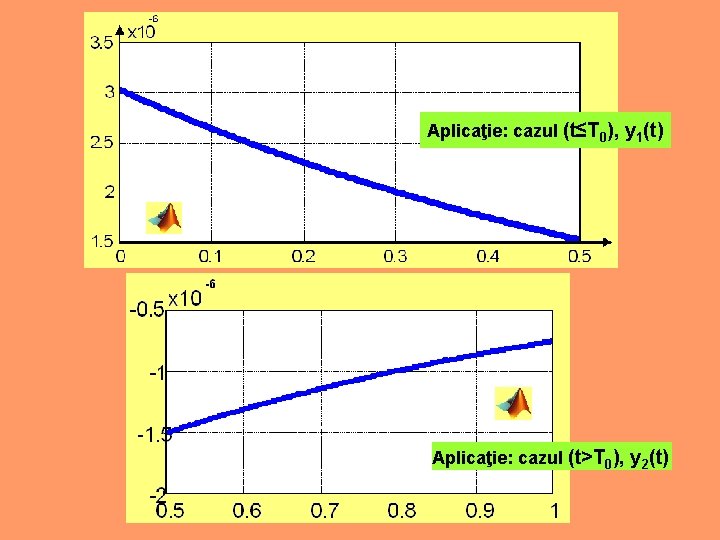
Exemplul numeric: R=330 k , C=2. 2 F, U 0=1, T 0 =0. 5 s » t=0: 0. 001: 0. 5; » y 1=(1/330000)*exp(-t/0. 726); plot(t, y 1); grid » t=0. 5: 0. 0001: 1; » y 2=-(1/330000)*(1 -exp(-0. 5/0. 726))*exp(-(t-0. 5)/0. 726); » plot(t, y 2); grid

Aplicaţie: cazul (t≤T 0), y 1(t) Aplicaţie: cazul (t>T 0), y 2(t)

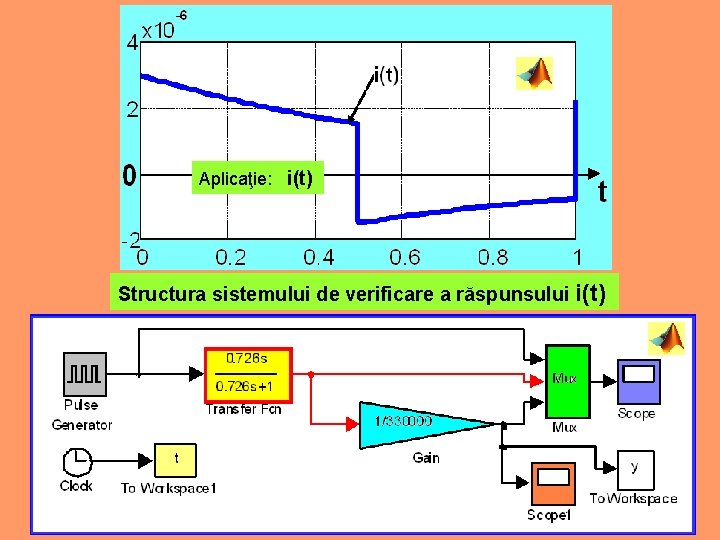
Aplicaţie: i(t) Structura sistemului de verificare a răspunsului i(t)

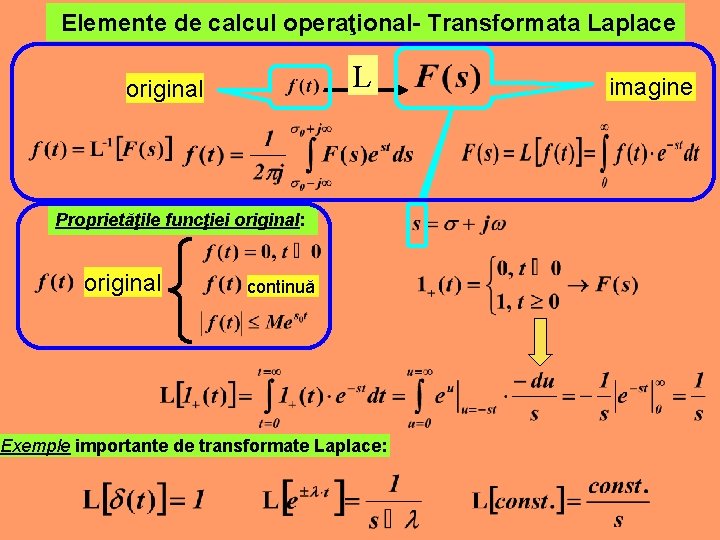
Elemente de calcul operaţional- Transformata Laplace L original Proprietăţile funcţiei original: original continuă Exemple importante de transformate Laplace: imagine

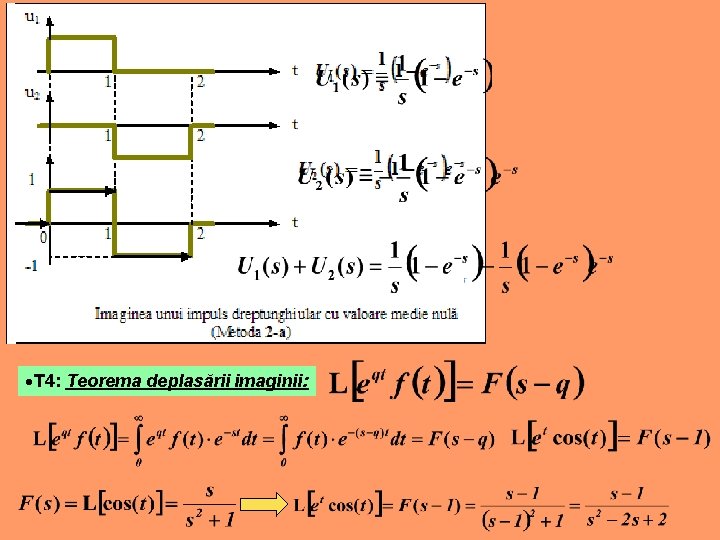
Teoreme ale transformatei Laplace: T 1: Transformata Laplace este o transformată liniară. Aditivitate: omogenitate: T 2: Teorema asemănării originalului

T 3: Teorema întârzierii originalului


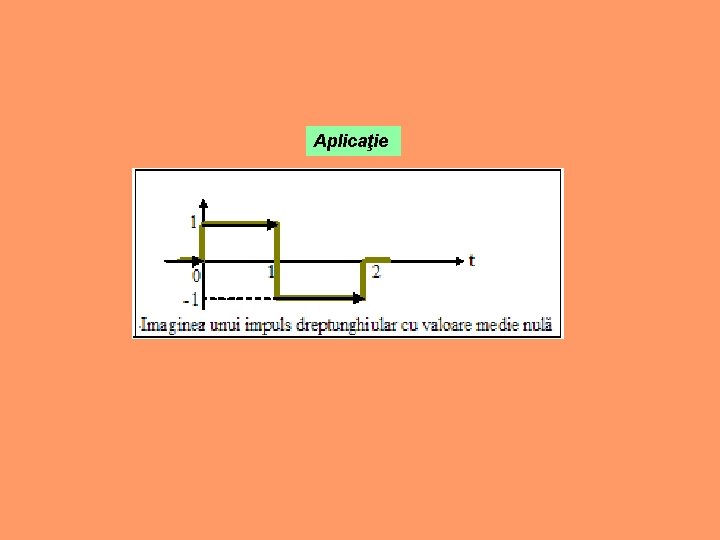
Pentru impulsul dublu dreptunghiular cu factorul de umplere ( ) şi perioadă (T), forma compactă este:


Aplicaţie


T 4: Teorema deplasării imaginii:

T 5: Teorema derivării originalului:

T 6: Teorema derivării imaginii T 7: Teorema integrării originalului:

T 8: Teorema integrării imaginii:

T 9: Teorema produsului a două imagini (produsul de convoluţie):

T 11: Teorema I-a de dezvoltare a lui Heaviside:

T 12: Teorema II-a de dezvoltare a lui Heaviside: Dacă polul sk are ordinul de multiplicitate qk, k=1, 2, …, n, atunci: Dacă Y(s) este o fracţie raţională cu un pol în origine, atunci ea este imaginea funcţiei original:

Exemplul

» ilaplace(-a*j/4/(s+a*j)^2) ans =-1/4*i*a*t*exp(-i*a*t) » ilaplace(a*j/4/(s-a*j)^2) ans =1/4*i*a*t*exp(i*a*t) » simplify(ilaplace(-a*j/4/(s+a*j)^2)+ilaplace(a*j/4/(s-a*j)^2)) ans =-1/2*a*t*sin(a*t) » ilaplace(a^4/s/(s^2+a^2)^2) ans =a^4*(1/a^4 -1/a^4*cos(a*t)-1/2/a^3*t*sin(a*t))

» syms a s » Y=a^4/s/(s^2+a^2)^2; » A=limit(s*Y, s, 0) » B=limit((s+a*i)^2*Y, s, -a*i) B=-1/4*i*a » C=limit(diff((s+a*i)^2*Y), s, -a*i) C=-1/2 » D=limit((s-a*i)^2*Y, s, a*i) D=1/4*i*a » E=limit(diff((s-a*i)^2*Y), s, a*i) T 13: Teorema valorii finale:

T 14: Teorema valorii iniţiale:

 Cele 12 nevoi fundamentale
Cele 12 nevoi fundamentale Regimuri politice postbelice
Regimuri politice postbelice Marimi fundamentale
Marimi fundamentale Attribusjon
Attribusjon Cele 14 nevoi fundamentale lucretia titirca
Cele 14 nevoi fundamentale lucretia titirca Nevoia de a respira si a avea o buna circulatie
Nevoia de a respira si a avea o buna circulatie Cicluri curriculare
Cicluri curriculare Fundamentale aktienanalyse kennzahlen
Fundamentale aktienanalyse kennzahlen Etapele procesului de ingrijire
Etapele procesului de ingrijire Proprietatile chimice ale apei ppt
Proprietatile chimice ale apei ppt Priama charakteristika osoby
Priama charakteristika osoby Boli ale sistemului nervos
Boli ale sistemului nervos Randamentul unui motor termic
Randamentul unui motor termic Materiale metalice clasificare
Materiale metalice clasificare Cele 8 minuni ale lumii
Cele 8 minuni ale lumii Efectul fotoelectric referat
Efectul fotoelectric referat Absorbtia si circulatia apei in planta sunt influentate
Absorbtia si circulatia apei in planta sunt influentate Radiatiile x referat fizica
Radiatiile x referat fizica Procese volitive
Procese volitive I ale
I ale Ghidul meseriilor viitorului 2020
Ghidul meseriilor viitorului 2020 Conditii interne si externe ale invatarii
Conditii interne si externe ale invatarii Morala despre curaj
Morala despre curaj Frana hidraulica pascal
Frana hidraulica pascal Tablitele sumeriene
Tablitele sumeriene Poluarea aerului prin produse gazoase ale arderii
Poluarea aerului prin produse gazoase ale arderii Zonele biogeografice ale terrei ppt
Zonele biogeografice ale terrei ppt Pasari vestitoare ale primaverii
Pasari vestitoare ale primaverii Forta lui arhimede
Forta lui arhimede Ufaj ale sprawdzaj lenin
Ufaj ale sprawdzaj lenin Importanta litosferei
Importanta litosferei Reactia de ardere a metanolului
Reactia de ardere a metanolului Categoriile gramaticale ale verbului
Categoriile gramaticale ale verbului Apotema trunchiului de piramida
Apotema trunchiului de piramida Domeniile de viata ale terrei
Domeniile de viata ale terrei Atitudini si comportamente inacceptabile ale profesorului
Atitudini si comportamente inacceptabile ale profesorului Formarea statelor unite ale americii
Formarea statelor unite ale americii Clasificarea filetelor
Clasificarea filetelor Particularitati ale sistemului nervos la vertebrate
Particularitati ale sistemului nervos la vertebrate Marile descoperiri geografice
Marile descoperiri geografice Unitatile functionale ale calculatorului
Unitatile functionale ale calculatorului Tulpini aeriene ale plantelor
Tulpini aeriene ale plantelor Aplicatiile legii lui arhimede
Aplicatiile legii lui arhimede Change layer
Change layer Resurse permanente
Resurse permanente Sistemul digestiv boli
Sistemul digestiv boli Care sunt gradele de comparatie
Care sunt gradele de comparatie