PROGRAMMATION SCIENTIFIQUE EN C PRO1027 Rsolution de systme

PROGRAMMATION SCIENTIFIQUE EN C PRO-1027

Résolution de système d’équations linéaires (SVD et méthodes itératives) • • • Approche SVD (suite …) Approche LU (décomposition) Introduction (méthodes itératives) Méthode de Jacobi Méthode de Gauss-Seidel Considérations sur la convergence

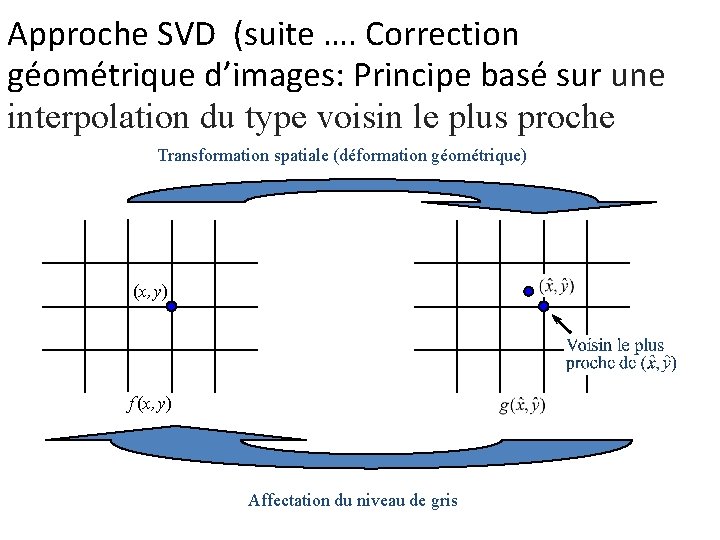
Approche SVD (suite …. Correction géométrique d’images: Principe basé sur une interpolation du type voisin le plus proche Transformation spatiale (déformation géométrique) (x, y) f (x, y) Affectation du niveau de gris

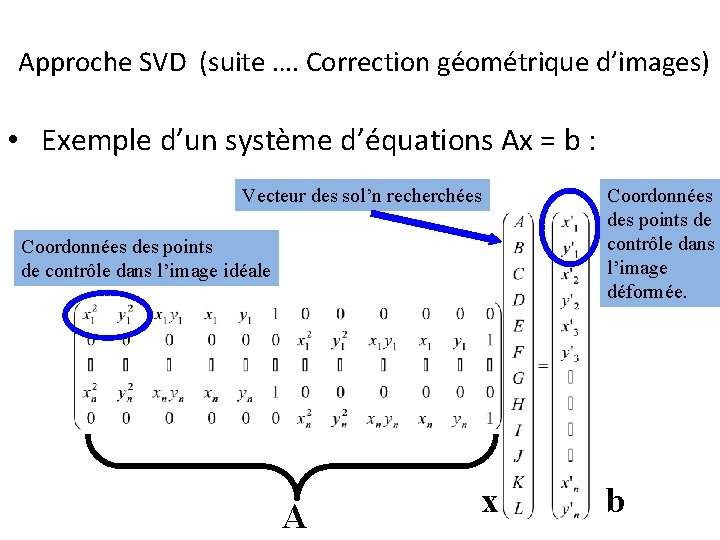
Approche SVD (suite …. Correction géométrique d’images) • Exemple d’un système d’équations Ax = b : Vecteur des sol’n recherchées Coordonnées des points de contrôle dans l’image idéale A x Coordonnées des points de contrôle dans l’image déformée. b

Approche SVD (suite …. Correction géométrique d’images) • Exemple d’un système d’équations Ax = b : Modèle de déformation géométrique

Approche SVD (suite …. Correction géométrique d’images ) • L’approche SVD permet d’exprimer la matrice A par la décomposition A = U W VT. • Cette décomposition en matrices est obtenue par la fonction svdcmp() de Numerical Recipes in C. • Les matrices U, W et VT permettent de calculer l’inverse de A, A-1 ayant la forme A-1 = (VT)-1 W-1 U-1 = V W-1 UT • V et U étant orthonormales, leur inverse est donc donnée par leur transposée. • W étant diagonale, donc W-1 est aussi diagonale avec les éléments sur la diagonale à 1/wi.

Approche SVD (suite …. Correction géométrique d’images) • Quand certaines valeurs wi 0 (proche de 0), la matrice A est dite singulière. • Dans ce cas, A-1 (VT)-1 W-1 U-1 V W-1 UT. • Donc pour estimer la matrice A-1 (pseudoinverse de A), nous remplaçons les valeurs 1/wi dans la matrice W-1 par 0 quand wi est petit (proche de 0). • Donc, x = A-1 b est obtenue dans les cas de singularité par x = pseudoinverse (A) b

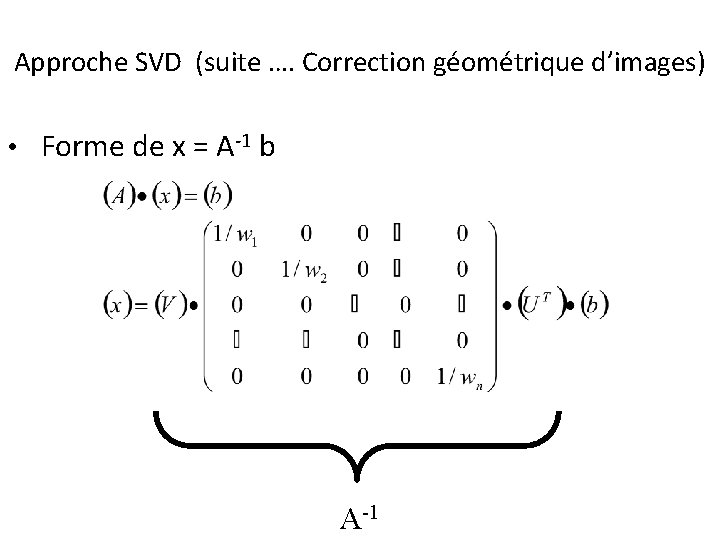
Approche SVD (suite …. Correction géométrique d’images) • Forme de x = A-1 b A-1

Approche SVD (suite …. Correction géométrique d’images) • Avant d’appeler la fonction svbksb() il faut vérifier si A est singulière. • Les wi < MAX(wi) * 1. 0 e-6 sont fixés à 0 dans la matrice W.

Approche SVD (suite …. Correction géométrique d’images) • Algorithme de résolution int X[20], Y[20], X_Prime[20], Y_Prime[20]; float wmax, wmin, **a, **u, *w, **v, *b, *x int i, j; // selectionner un minimum de 6 points de contrôle …. // selectionner un maximum de 20 points de contrôle // premier indice de X, Y, X_Prime et Y_Prime est 1 // m est le nombre de points de contrôle selectionnes a = matrix(1, 2*m, 1, 12); // matrice A de 2 m. X 12 u = matrix(1, 2*m, 1, 12); // m: nombre de points de contrôle w = vector(1, 12); v = matrix(1, 12, 1, 12); b = vector(1, 2*m); // points de contrôle dans l’image deformee x = vector(1, 12); // vecteur des sol’n …. . // mise à 0 de A

Approche SVD (suite …. Correction géométrique d’images) • Algorithme de résolution (suite for(i=1; i<=2*m; i+=2) // initialiser la matrice A { a[i][1] = a[i+1][7] = X[i/2+1]*X[i/2+1]; a[i][2] = a[i+1][8] = Y[i/2+1]*Y[i/2+1]; a[i][3] = a[i+1][9] = X[i/2+1]*Y[i/2+1]; a[i][4] = a[i+1][10] = X[i/2+1]; a[i][5] = a[i+1][11] = Y[i/2+1]; a[i][6] = a[i+1][12] = 1. 0; } …)

Approche SVD (suite …. Correction géométrique d’images) • Algorithme de résolution (suite …) for(i=1; i<=2*m; i+=2) // initialiser le vecteur b { b[i] = X_Prime[i/2+1]; b[i+1] = Y_Prime[i/2+1]; }

Approche SVD (suite …. Correction géométrique d’images) • Algorithme de résolution (suite …) for(i=1; i<=2*m; i++) for(j=1; j<=12; j++) u[i][j] = a[i][j]; svdcmp(u, 2*m, 12, w, v); wmax = 0. 0; for(j=1; j<=12; j++) if(w[j] > wmax) wmax = w[j]; wmin = wmax*1. 0 e-6; for(j=1; j<=12; j++) if(w[j] < wmin) w[j]=0. 0; // Eliminer les // singularites svbksb(u, w, v, 2*m, 12, b, x);

Approche SVD (suite …. Correction géométrique d’images) • Avec le vecteur des sol’n x dont les éléments correspondent aux coefficients des équations de transformation des pixels de l’image idéale vers l’image déformée. (x[1] A, x[2] B, x[3] C, x[4] D, …. ) x’ = A x 2 + B y 2 + C xy + D x + E y + F y’ = G x 2 + H y 2 + I xy + J x + K y + L (1) (2)

Approche SVD (suite …. Correction géométrique d’images) • En substituant les notations utilisées dans l’algorithme, les éq. (1) et (2 ) deviennent: X’ = x[1] X 2 + x[2] Y 2 + x[3] XY + x[4] X + x[5] Y + x[6] Y’ = x[7] X 2 + x[8] Y 2 + x[9] XY + x[10] X + x[11] Y + x[12]

Approche SVD (suite …. Correction géométrique d’images) • Algorithme de la correction géométrique for(Y=0; Y<Hauteur; Y++) // pour chaque rangée for(X=0; X<Largeur; X++) { // pour chaque colonne X’ = x[1] X 2 + x[2] Y 2 + x[3] XY + x[4] X + x[5] Y + x[6]; Y’ = x[7] X 2 + x[8] Y 2 + x[9] XY + x[10] X + x[11] Y + x[12]; // valider X’ Y’ image. Corrigee[Y][X] = image. Deforme[(int)Y’+0. 5][(int)X’+0. 5]; } // Ne pas oublier de libérer les matrices et vecteurs avec les fonctions free_matrix() // et free_vector()

Interpolation du type voisin le plus proche ["Nearest neighbor"] Transformation spatiale (x, y) f (x, y) Affectation du niveau de gris

Exemple: Correction géométrique – Résultat de la correction r 11 CGEO. rast r 11. rast correctiongeo r 11. rast r 11 CGEO. rast 1258 842 cadastre. NS 4 X 4. tiff 338 1180 3. 617372 e-5. . .

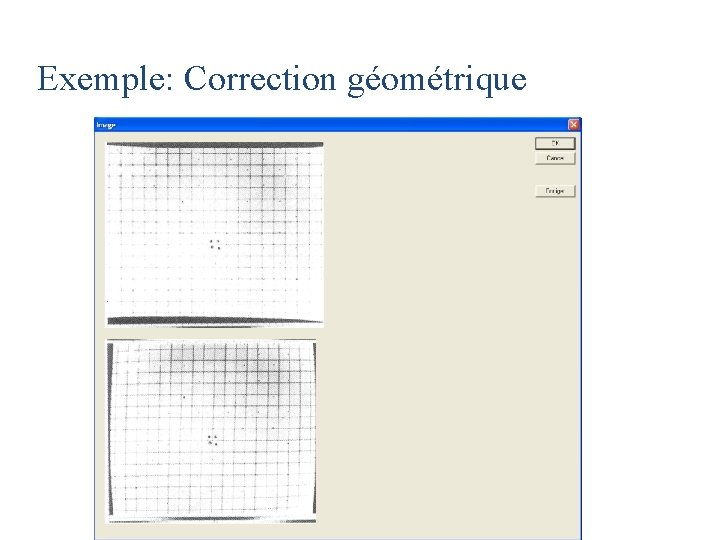
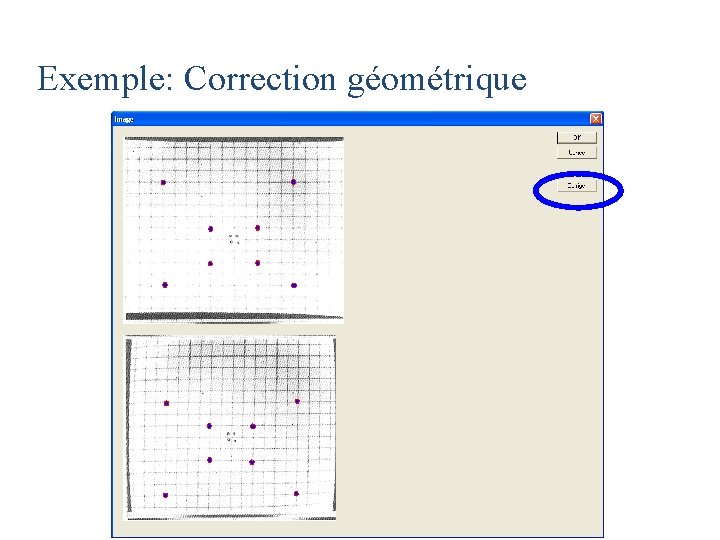
Exemple: Correction géométrique

Exemple: Correction géométrique

Approche SVD (Approximation d’une région dans une image par une ellipse) • Sachant qu’un ensemble de points 2 D dans une image peut être approximés par une ellipse de la forme: 0 = A x 2 + 2. 0 B xy + C y 2 + 2. 0 D x + 2. 0 F y + G (1) • Les coefficients de l‘équation (1) (ellipse d‘approximation) doivent être trouvés. • Nous devons alors résoudre un système de la forme Ax = 0 ou x est le vecteur sol‘n (coefficients). • Nous pouvons utiliser l‘équation (1) pour tracer l‘ellipse d‘approximation de la forme dans l‘image.

Approche SVD (Approximation d’une région dans une image par une ellipse) • Exemple d’un système d’équations Ax = 0 : Coordonnées des points dans l’image Vecteur des sol’n recherchées A x b

Approche SVD (suite …. Approximation de forme par ellipse) • Algorithme de résolution int X[20], Y[20]; // pour 20 pixels selectionnes max. float wmax, wmin, **a, **u, *w, **v, *b, *x int i, j; // selectionner un minimum de 6 points a approximer …. // selectionner un maximum de 20 points a approximer // premier indice de X, Y, est 1 m est le nombre de points selectionnes a = matrix(1, m, 1, 6); // matrice A de m. X 6 u = matrix(1, m, 1, 6); // m: nombre de points a approximer w = vector(1, 6); v = matrix(1, 6, 1, 6); b = vector(1, m); // 0 x = vector(1, 6); // vecteur des sol’n …. . // mise à 0 de A

Approche SVD (suite …. Approximation de forme par ellipse) • Algorithme de résolution (suite …) for(i=1; i<=m; i+=1) // initialiser la matrice A { a[i][1] = X[i]*X[i]; a[i][2] = 2. 0*X[i]*Y[i]; a[i][3] = Y[i]*Y[i]; a[i][4] = 2. 0*X[i]; a[i][5] = 2. 0*Y[i]; a[i][6] = 1. 0; } for(i=1; i<=m; i+=1) // initialiser le vecteur b { b[i] = 0. 0; }

Approche SVD (suite …. Approximation de forme par ellipse) u Algorithme de résolution (suite …) for(i=1; i<=m; i++) for(j=1; j<=6; j++) u[i][j] = a[i][j]; svdcmp(u, m, 6, w, v); wmax = 0. 0; for(j=1; j<=6; j++) if(w[j] > wmax) wmax = w[j]; wmin = wmax; // trouver la valeur propre min. dans w for(j=1; j<=6; j++) if((w[j] < wmin) && w[j] != 0. 0) {wmin = w[j]; min. Pos = j; } for(j=1; j<=6; j++) x[j]=v[j][min. Pos]; // x contient la solution

Approche SVD (suite …. Approximation de forme par ellipse) • Avec le vecteur des sol’n x dont les éléments correspondent aux coefficients de l’équation de l’ellipse d’approximation de la forme dans l’image. (x[1] A, x[2] B, x[3] C, x[4] D, …. ) 0 = A x 2 + 2. 0 B xy + C y 2 + 2. 0 D x + 2. 0 F y + G (1) • Nous pouvons ensuite utiliser l‘équation (1) pour tracer l‘ellipse d‘approximation de la forme dans l‘image. Plus spécifiquement vous passer le vecteur x des sol‘n à la fonction de tracage de l‘ellipse.

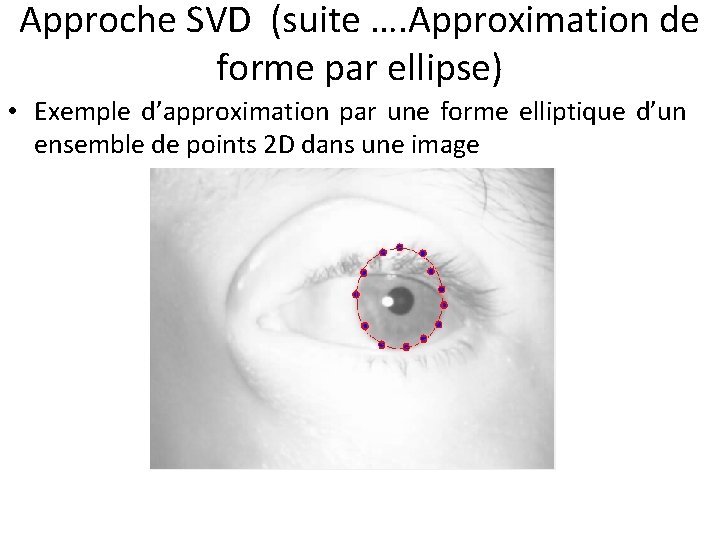
Approche SVD (suite …. Approximation de forme par ellipse) • Exemple d’approximation par une forme elliptique d’un ensemble de points 2 D dans une image

Approche LU (Décomposition) • Si nous pouvons écrire la matrice A utilisée dans le système Ax = b, sous forme d‘une multiplication de 2 matrices L U, par exemple pour une matrice A de 4 X 4: L U • Le système linéaire Ax=b peut alors être réécrit: • Avec y = U x alors: et avec la sol‘n y:

Approche LU (Décomposition) • Il est ensuite trivial par substitution avant de déduite le vecteur y: • Et ensuite le vecteur x par subtitution arrière:

Approche LU (Décomposition) • Comment alors déduire les matrices L et U, sachant que les termes aij sont déduits par: • Le nombre de termes de cette somme dépend de si i ou j est le plus petit. Trois cas sont alors possibles:

Approche LU (Décomposition: voir EXLU) • Algorithme de Crout pour déduire la matrice LU: – Initialisation: Pour j allant de 1 à N Pour i allant de 1 à j // i < j Si i == 1 Alors 1 j = 1 j Sinon Finsi Fin Pour i allant de j+1 à N // i > j Fin Pour i<j i>j

Approche LU (Décomposition) • Algorithme de Crout (prototype de la fonction de décomposition) INPUT: Matrice a[1. . n] OUTPUT: Matrice LU OUTPUT: vecteur de permutations INPUT: vecteur b[1. . n] OUTPUT: vecteur x[1. . n] sol’n

Introduction (approches itératives) • Les méthodes d’élimination sont des méthodes de résolution directes puisque le nombre d’opérations est connu. • Nous pouvons cependant résoudre un système d’équations linéaires par une procédure d’essai et erreur. • Cette procédure suppose une solution de départ qui représente une estimation des valeurs des inconnus.

Introduction (approches itératives) • De façon itérative, les estimées de la solution sont raffinées jusqu’à ce qu’un critère d’arrêt soit atteint. • Les avantages des méthodes itératives sont d’être plus rapides que les méthodes directes et qu’elles peuvent être utilisées pour résoudre des systèmes non-linéaires.

La méthode de Jacobi • Par la méthode de Jacobi nous pouvons isoler chaque inconnu Xi de la façon suivante:

La méthode de Jacobi • Algorithme de Jacobi (une itération) Jacobi(int dim, float **a, float *c, float *x, float *y) /* x contient l’estimation actuelle de la solution y contient la nouvelle estimation de la solution */ POUR i allant de 1 à dim FAIRE y[i] = c[i] POUR j allant de 1 à dim FAIRE SI j != i ALORS y[i] = y[i]- a[i, j] * x[j] FIN SI FIN POUR y[i] = y[i]/ a[i, i] FIN POUR

La méthode de Jacobi • Algorithme de Jacobi (général) Jacobi. G(int dim, float **a, flaot *c) assignation du vecteur x initial et y aux mêmes valeurs erreur = MAXFLOAT TANT QUE erreur > eps FAIRE POUR i allant de 1 à dim FAIRE x[i]=y[i] FINTANTQUE Jacobi(dim, a, c, x, y) /* Gauss-Seidel() */ erreurmax = 0 POUR i allant de 1 à dim FAIRE /* Calcul de l ’erreur */ erreur = | y[i]- x[i] | SI erreur > erreurmax ALORS erreurmax = erreur FINSI FIN POUR erreur = erreurmax FINTANTQUE imprimer le vecteur y

La méthode de Gauss-Seidel • Pour accélérer le taux de convergence pourquoi ne pas insérer les nouvelles estimations dans les équations suivantes pour donner:

La méthode de Gauss-Seidel u Algorithme de Gauss-Seidel (une itération) Gauss. Seidel(int dim, float **a, float *c, float *x, float *y) /* x contient l’estimation actuelle de la solution y contient la nouvelle estimation de la solution */ POUR i allant de 1 à dim FAIRE y[i] = c[i] POUR j allant de 1 à i-1 FAIRE y[i] = y[i]- a[i, j] * y[j] FIN POUR j allant de i+1 à dim FAIRE y[i] = y[i]- a[i, j] * x[j] FIN POUR y[i] = y[i]/ a[i, i] FIN POUR

Considérations sur la convergence u Pour que les méthodes de Jacobi et Gauss-Seidel convergent il faut que la condition suivante soit respectée

Considérations sur la convergence u Quand cette condition est vraie, les algorithmes itératifs convergent vers la solution indépendamment du choix du vecteur solution x 1 initial. u Une matrice des coefficients qui possède cette propriété est appelée matrice à diagonale dominante. u Lorsque la matrice a ne respecte pas cette condition nous pouvons permuter des rangées de façon à respecter cette condition.

Considérations sur la convergence u Si nous avons un système de 2 inconnus de la forme: u Nous pouvons isoler les inconnus:

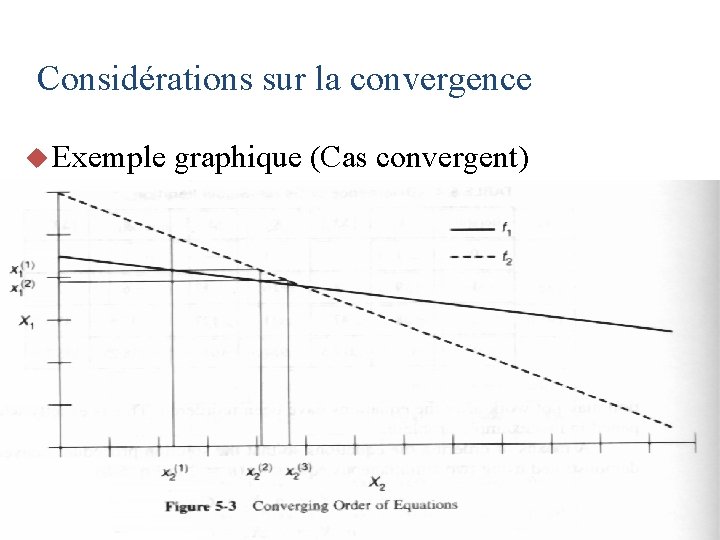
Considérations sur la convergence u Exemple graphique (Cas convergent)

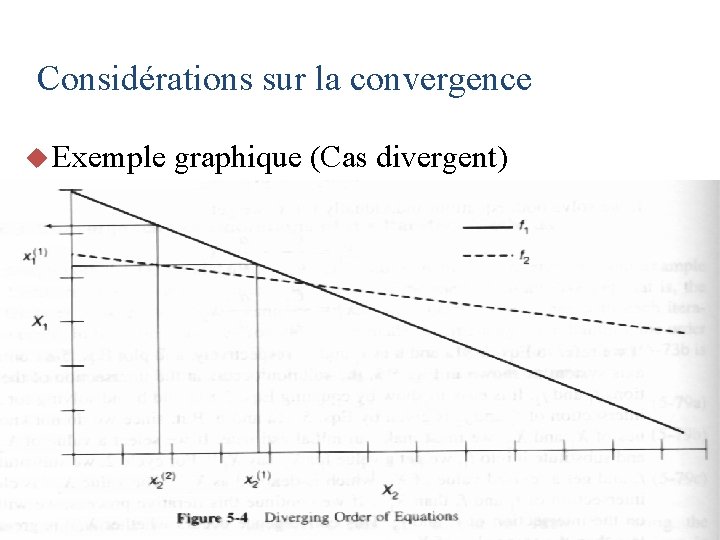
Considérations sur la convergence u Exemple graphique (Cas divergent)