PROGRAMMATION SCIENTIFIQUE EN C PRO1027 Interpolation extrapolation de

PROGRAMMATION SCIENTIFIQUE EN C PRO-1027

Interpolation/ extrapolation de fonctions • Introduction • Méthode de Gregory-Newton • Méthode de Lagrange – Algorithme d’interpolation – Algorithme de Neville

Introduction • Dans plusieurs problèmes nous avons en main un ensemble de mesures discrètes • Nous voulons souvent connaître le comportement du phénomène mesuré entre chaque mesure discrète • Nous devons alors interpoler les intervalles de valeurs entre chaque mesure discrète à l’aide de fonctions de degré quelconque

Introduction u Si nous avons un polynôme d’interpolation f(x) de degré n: u Les n+1 coefficients du polynôme sont déduits à partir des n+1 points de contrôle (mesures)

Introduction • Interpolation linéaire u Deux points de contrôle (mesures) sont nécessaires pour déduire les coefficients inconnus u Une fonction d’interpolation de degré n requiert donc n+1 points de contrôle (mesures)

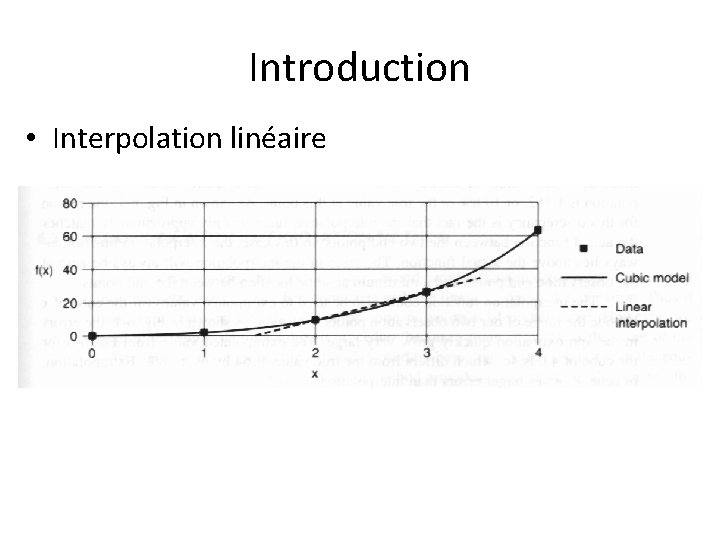
Introduction • Interpolation linéaire

Introduction • Interpolation linéaire – Par la loi des triangles semblables nous savons: – Si f(x) est mis en évidence: PENTE DÉVIATION PAR RAPPORT à xi

Introduction • Interpolation linéaire – Ce type d’interpolation peut causer des erreurs importantes lorsque le polynôme réel est d’ordre supérieur au polynôme d’interpolation (Voir l’intervalle [2, 3]) – Pour améliorer la précision de l’interpolation nous devons utiliser des polynômes de degrés supérieurs

Introduction • Interpolation non linéaire – Prenons par exemple un polynôme de degré 2 – Nous devons alors utiliser 3 points de contrôle pour déduire les valeurs des coefficients – Si nous généralisons cette approche, nous pouvons alors utiliser un polynôme d’interpolation de degré n avec n+1 coefficients et qui requière n+1 points de contrôle pour déduire les valeurs des coefficients

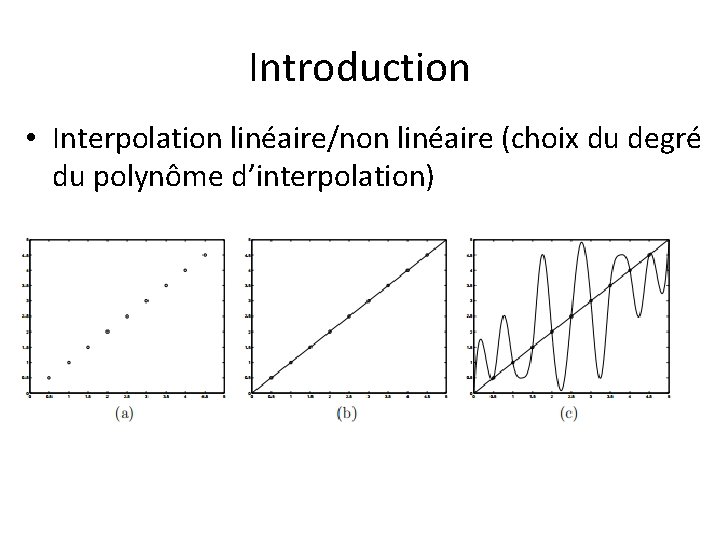
Introduction • Interpolation linéaire/non linéaire (choix du degré du polynôme d’interpolation)

Introduction • Interpolation linéaire/non linéaire (choix du degré du polynôme d’interpolation) Une fonction lisse est interpolée plus précisément par un polynôme de degré supérieur Une fonction avec des changements brusques est interpolée plus difficilement par un polynôme de degré supérieur

Méthode de Gregory-Newton • Cette méthode permet de déduire un polynôme d’interpolation de degré n sans avoir à résoudre un système d’équations linéaires • Le polynôme d’interpolation déduit par cette méthode est de la forme: u Les n+1 valeurs de xi (intervalles en x égaux) et f(xi) sont connues, les n+1 valeurs des coefficients ai sont inconnues et doivent être déduites

Méthode de Gregory-Newton • Si les valeurs de x sont en ordre croissant nous pouvons alors déduire les coefficients ai par: u Nous répétons ces calculs pour les n+1 coefficients ai.

Méthode de Gregory-Newton • Le polynôme de Gregory-Newton sous sa forme généralisée:

Méthode de Gregory-Newton u Le polynôme de Gregory-Newton sous sa forme généralisée (calcul des coefficients ai):

Méthode de Gregory-Newton • Le polynôme de Gregory-Newton sous sa forme généralisée

Méthode de Gregory-Newton • Le polynôme de Gregory-Newton sous sa forme généralisée (forme récursive):

Méthode de Lagrange • Lorsque les intervalles en x sont inégaux il faut utiliser une autre forme de polynôme d’interpolation • Le polynôme de Lagrange de degré n-1 est utilisé dans ces circonstances. Sa forme générale est donnée par:

Méthode de Lagrange • Le polynôme de Lagrange de degré n-1 est utilisée dans ces circonstances. Sa forme générale est donnée par (voir Numerical Recipes):

Méthode de Lagrange • Les fonctions cardinales li(x) sont données par:

Méthode de Lagrange • Les fonctions cardinales li(x) sont données par (n = 3):

Méthode de Lagrange • Les fonctions cardinales li(x 1) sont données par (n = 3):

Méthode de Lagrange • Les fonctions cardinales li(x 1) sont données par (n = 3):

Méthode de Lagrange • Algorithme Lire les xi Lire les yi Pour m valeurs de x dans l’intervalle [minx, maxx] FAIRE Calculer Écrire x et f(x) dans un fichier FIN POUR

Méthode de Lagrange • Par exemple avec n points = 2 (degré 1) – on a donc 2 points (x 0, y 0) et (x 1, y 1) – on cherche la droite y=ax+b (polynôme de degré 1) qui passe par ces 2 points

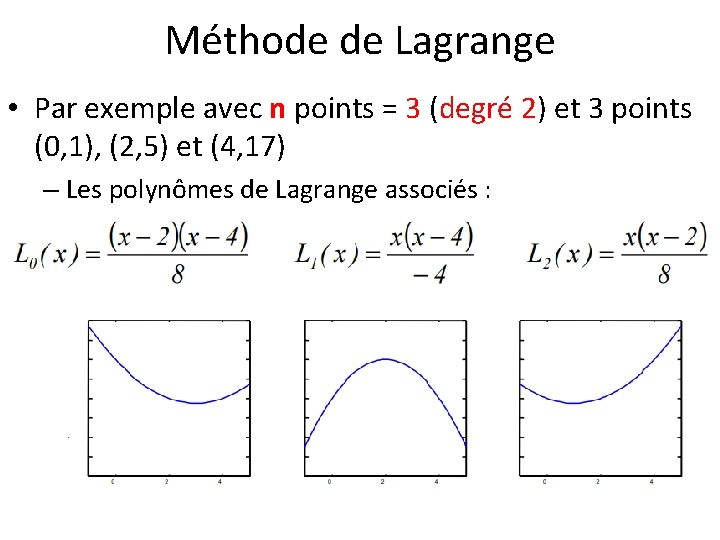
Méthode de Lagrange • Par exemple avec n points = 3 (degré 2) et 3 points (0, 1), (2, 5) et (4, 17) – Les polynômes de Lagrange associés :

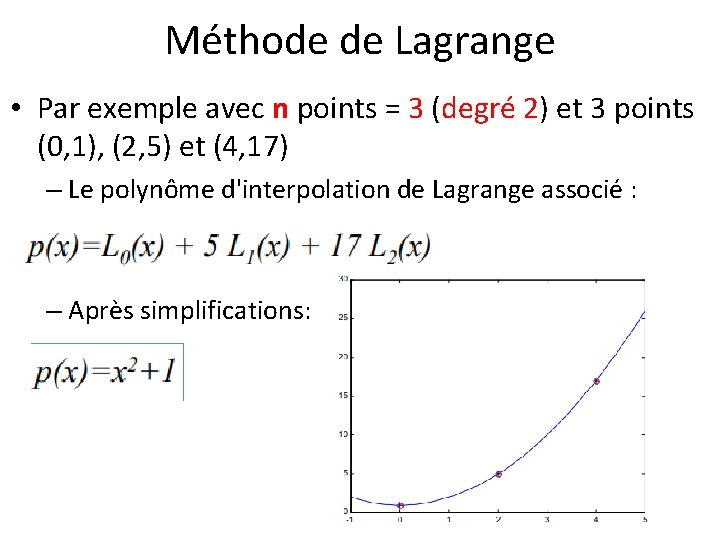
Méthode de Lagrange • Par exemple avec n points = 3 (degré 2) et 3 points (0, 1), (2, 5) et (4, 17) – Le polynôme d'interpolation de Lagrange associé : – Après simplifications:

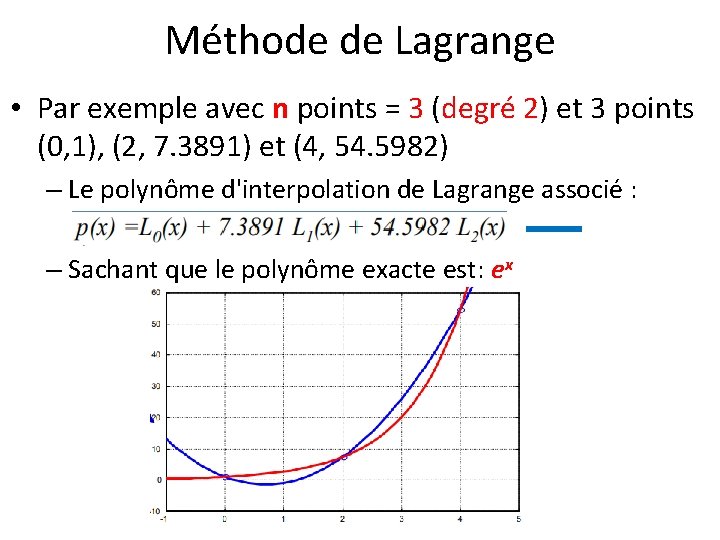
Méthode de Lagrange • Par exemple avec n points = 3 (degré 2) et 3 points (0, 1), (2, 7. 3891) et (4, 54. 5982) – Le polynôme d'interpolation de Lagrange associé : – Sachant que le polynôme exacte est: ex

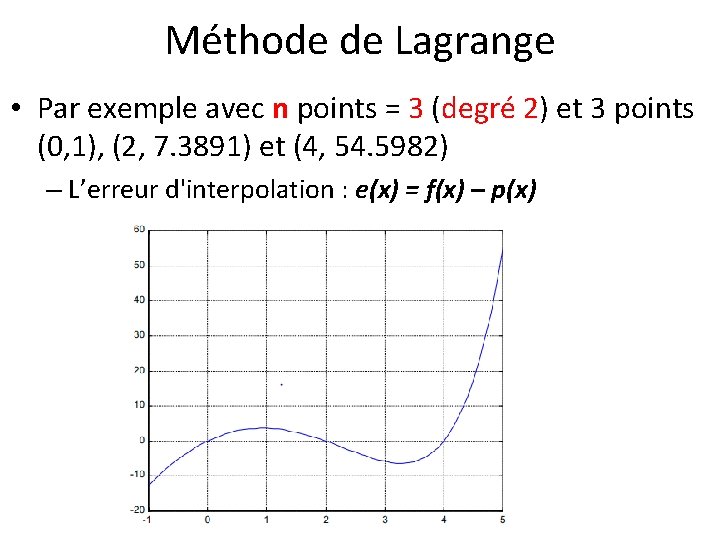
Méthode de Lagrange • Par exemple avec n points = 3 (degré 2) et 3 points (0, 1), (2, 7. 3891) et (4, 54. 5982) – L’erreur d'interpolation : e(x) = f(x) – p(x)

Méthode de Lagrange • Algorithme de Neville (voir Numerical Recipe) – Supposons que le nombre de points de contrôle est élevé pour interpoler la fonction idéale f() – faut-il tous les utiliser ? Rendant les calculs lourds – Avec la méthode de Neville • n (le nombre de points) est augmenté progressivement • les termes Li sont calculés de manière récursive • on arrête le processus dès que l'erreur est inférieure à un seuil prédéfini

Méthode de Lagrange • Algorithme de Neville (Voir Numerical Recipes) permet de déduire la fonction polynômiale P(x) de façon récursive (par exemple avec n points): Degré: 0 1 2 3

Méthode de Lagrange • Algorithme de Neville (Voir Numerical Recipes) permet de déduire la fonction polynômiale P(x) de façon récursive (par exemple avec n points):

Méthode de Lagrange • Algorithme de Neville (Voir Numerical Recipes) permet de déduire la fonction polynômiale P(x) de façon récursive (par exemple avec n points): C 1, 1 D 1, 1 C 2, 1 C 1, 2 D 2, 1 D 1, 2 C 1, 3 C 3, 1 C 2, 2 D 3, 1 D 2, 2 D 1, 3 C m, i D m, i m: nombre de points (niveaux) à partir du point de départ i Les termes C et D sont les différences entres les termes P

Méthode de Lagrange • Algorithme de Neville (Voir Numerical Recipes) permet de déduire la fonction polynômiale P(x) de façon récursive (termes de différences C et D):

Méthode de Lagrange • Algorithme de Neville (Voir Numerical Recipes) permet de déduire la fonction polynômiale P(x) de façon récursive:

Méthode de Lagrange (Voir l’exemple EX-LAGRANGE • Algorithme de Neville: fonction polint() dans Numerical Recipes: