PROGRAMMATION SCIENTIFIQUE EN C PRO1027 Drivation numrique Introduction

PROGRAMMATION SCIENTIFIQUE EN C PRO-1027

Dérivation numérique • Introduction • Dérivation numérique – Différences finies – Polynômes d’interpolation et d’approximation • Exemple: Cotes boursières

Introduction u Dans plusieurs problèmes nous avons besoin de calculer la dérivée d’une fonction u Deux approches existent pour résoudre ce problème u Une première, qui estime les valeurs de la dérivée lorsqu’une fonction est connue mais dont sa dérivée ne peut pas être déduite analytiquement u L’estimation de la dérivée peut se faire par une approche aux différences finies de la forme:

Introduction u Une seconde approche est de calculée la dérivée des polynômes d’interpolation ou d’approximation dont nous pouvons déduire la forme analytique

Dérivation numérique (différences finies) u Les méthodes aux différences finies découlent de la série de Taylor: u Si nous éliminons les termes d’ordre supérieur ou égal à 2 nous obtenons u En isolant le terme dérivé nous obtenons • Différence avant d’ordre 1

Dérivation numérique (différences finies) u L’approximation d’ordre 2 de la dérivée première de f(x) est obtenue en incluant un second terme à la série de Taylor: u Nous devons estimer d’abord la dérivée seconde en utilisant une méthode aux différences finies de la forme:

Dérivation numérique (différences finies) u Si nous substituons le résultat de l’estimation de la dérivée première par différence finie d’ordre 1 nous obtenons: • Approximation de premier ordre de la dérivée seconde u Nous pouvons alors déduire une approximation d’ordre 2 de la dérivée première:

Dérivation numérique (différences finies) u La dérivée seconde d’ordre 2 est alors déduite par: u En utilisant une méthode aux différences finies arrières nous obtenons les approximations d’ordre 1 et 2 suivantes pour la dérivée première:

Dérivation numérique (différences finies) u En utilisant une méthode aux différences finies arrières nous obtenons les approximations d’ordre 1 et 2 suivantes pour la dérivée seconde:

Dérivation numérique (différences finies) u En utilisant une méthode aux différences finies centrées nous obtenons les approximations d’ordre 1 et 2 suivantes pour la dérivée première:

Dérivation numérique (différences finies) u En utilisant une méthode aux différences finies centrées nous obtenons les approximations d’ordre 1 et 2 suivantes pour la dérivée seconde:

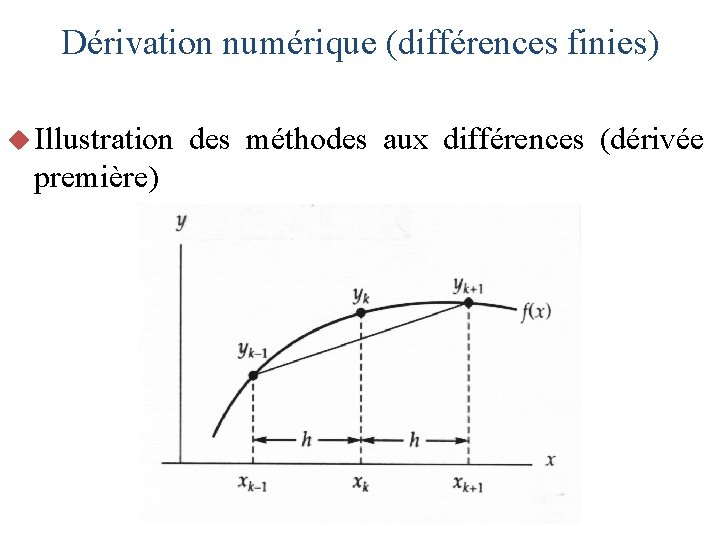
Dérivation numérique (différences finies) u Illustration première) des méthodes aux différences (dérivée

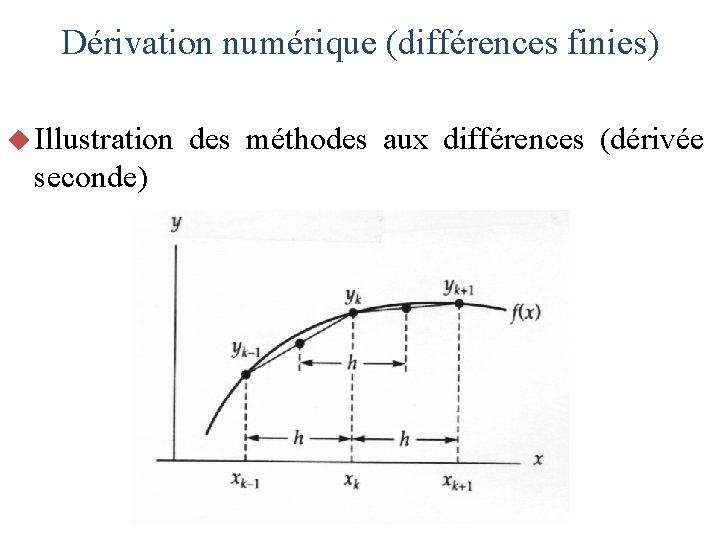
Dérivation numérique (différences finies) u Illustration seconde) des méthodes aux différences (dérivée

Dérivation numérique (différences finies) u Implémentation du calcul de la dérivée première par différence finie (Algorithme de Ridders dans Numerical Recipes in C) ……….

Dérivation numérique (Polynômes) u Les splines cubiques prennent la forme: u Leurs dérivées premières donnent: u Leurs dérivées secondes donnent:

Dérivation numérique (Polynômes) u Polynômes d’approximation (degré 1) u Polynômes d’approximation (degré 2)

Dérivation numérique (Polynômes) u Polynômes d’approximation (degré 3)

Dérivation numérique (Polynômes) u Polynômes d’approximation (degré 4)

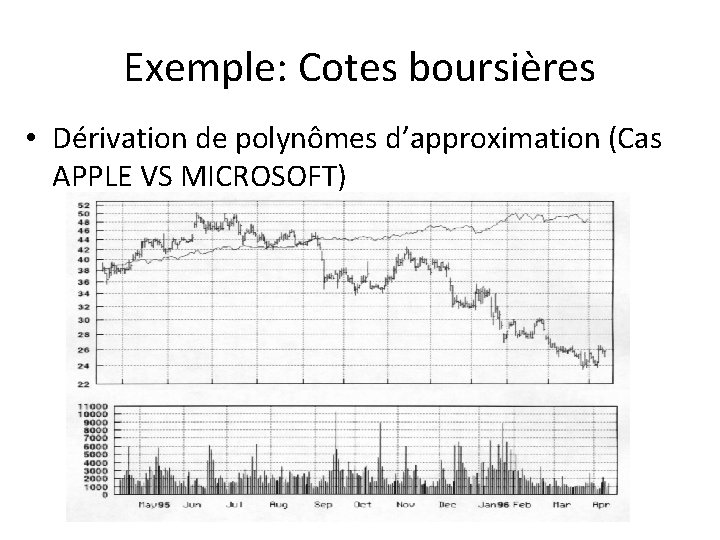
Exemple: Cotes boursières • Dérivation de polynômes d’approximation (Cas APPLE VS MICROSOFT)

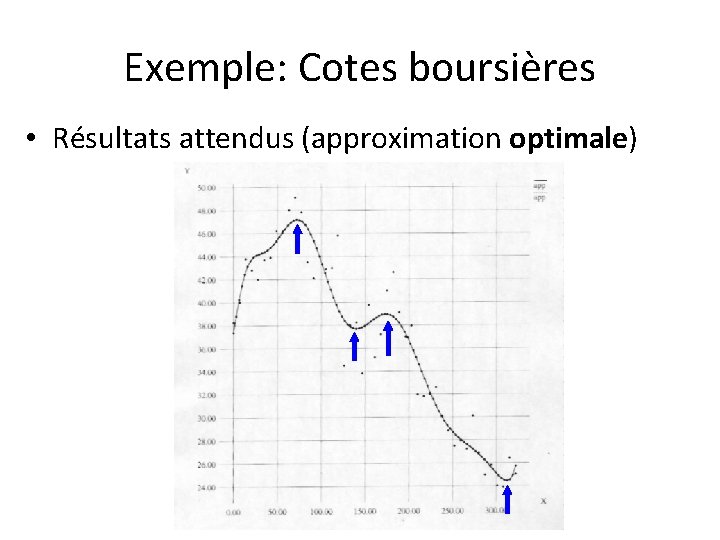
Exemple: Cotes boursières • Résultats attendus (approximation optimale)

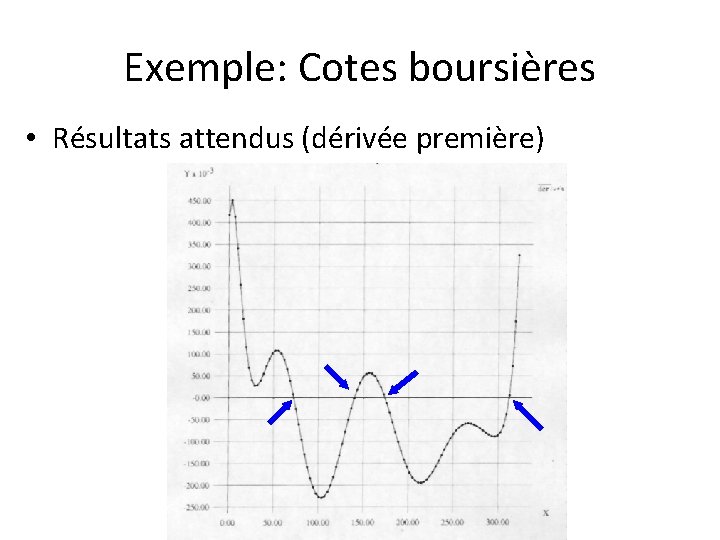
Exemple: Cotes boursières • Résultats attendus (dérivée première)