Science Engineering Technology Mathematics Integrating The STEM Disciplines

Science Engineering Technology Mathematics “Integrating The STEM Disciplines With Mousetrap Vehicles” 2016 ITEEA – Washington, D. C. National Harbor Conference Center Presenter Chuck Goodwin, DTE

Getting To STEM With Mouse Trap Vehicles Introduction • The Mouse Trap Vehicle is a TRUE STEM Machine! • An Integrated STEM Approach • Levels – Middle School & High School • Car Parts, Function, Construction, Adjustment • Physical Science (Physics) Principles • Mathematical analysis and modeling • Use of Technological Tools • Engineering Design Process

Our STEM Approach • Science – Physics: Forces, Motion, Units, Momentum, Spring Constant, Rate, Speed, Coefficient of Friction, etc. • Technology – Construction, Problem Solving, Resources, Tools, Machines, Computers, Sensors, Measurement, Timers, Video • Engineering – Optimization, Design, Modeling, Systems, Ethics, – Technology, Society, Integration • Math – Measurement, Basic Math, Geometry, Algebra, Trigonometry, Excel Spreadsheets

Levels • Middle School – Show car operating; cover springs, forces – Function of Parts, friction, Perform rate and speed calculations, Summative Writing – How much time do you have? • High School – Spring scale, vectors, kinetic & Potential Energy, Torque, Acceleration – Friction- (Kinetic, Static & Rolling) – Develop graphs and Work equations – Keep an Engineering Log – Summative Writing

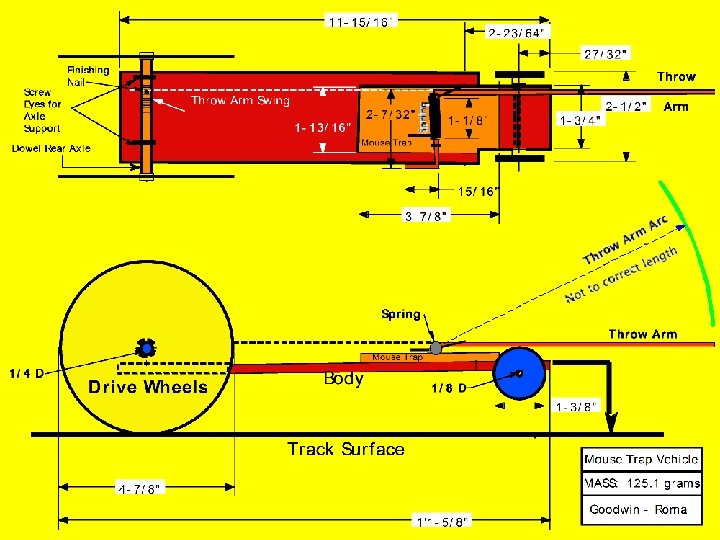
Vehicle Construction • • Safety First Measure and Record Parts Design – Sketches, Drafting or CAD Problem Solve, Plan Construction – Research how to get the best performance? • Kit or Scratch built Construction Options Advantages and Disadvantages • Weigh the Finished Vehicle (convert grams to lbs)

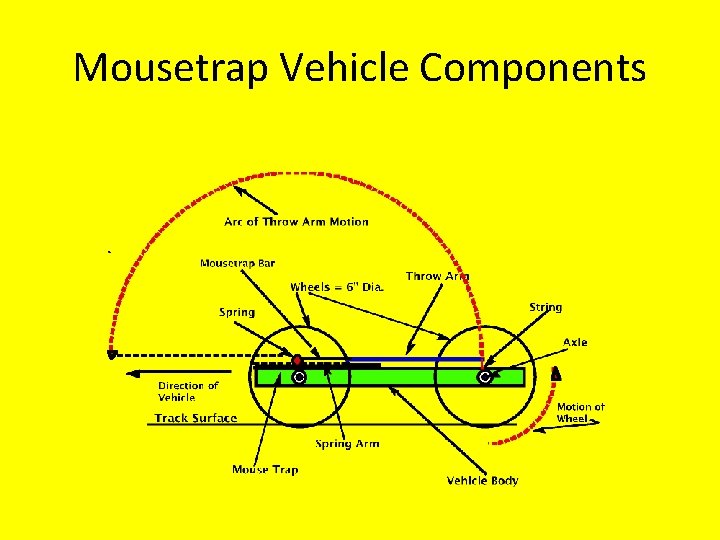
Mouse Trap Rear Drive Wheels ne h Li s i F r e Driv Vehicle Body Front Wheels es y E w Scre Throw Arm Plastic g Tubin St Dowel Rear Axle Front Axle sing Hou e l x A raw Finishing Nail Nomenclature - Parts Function

Mousetrap Vehicle Components

Physics • Where are forces involved? – Loading the trap (Potential Energy) – Springing the trap ( Kinetic Energy) – Transfer to the axle and Rear Wheels (Torque) – Transfer the force to the run way surface – Speed / Velocity / Distance of travel – Momentum

Forces [3] • Transfer of the force to the axle – Slippage – Axle, Fish Line, Wheel to Road • Torque applied to wheels (later) – “foot-pounds- Ftlb” “Newton-Meters-NM” • Wheel friction – Static – Kinetic – Rolling

Forces [4] Spring the Trap • Observe / time the trap after springing • Time various distances for speed Calculate the Force • Calculate the car speed immediately after the springing. • Calculate the acceleration and force

Force • • Force= mass x acceleration Newton’s 2 nd Law F = ma F = 2 kg x 9. 8 m/s 2 F = 19. 6 kg m/s 2 = 19. 6 Newtons 1 Newton =. 225 pounds 19. 6 Newtons x. 225 lbs / Newton= 4. 41 lbs F = 4. 41 lbs

Math [1] • Mousetrap bar length of travel • Bar extension

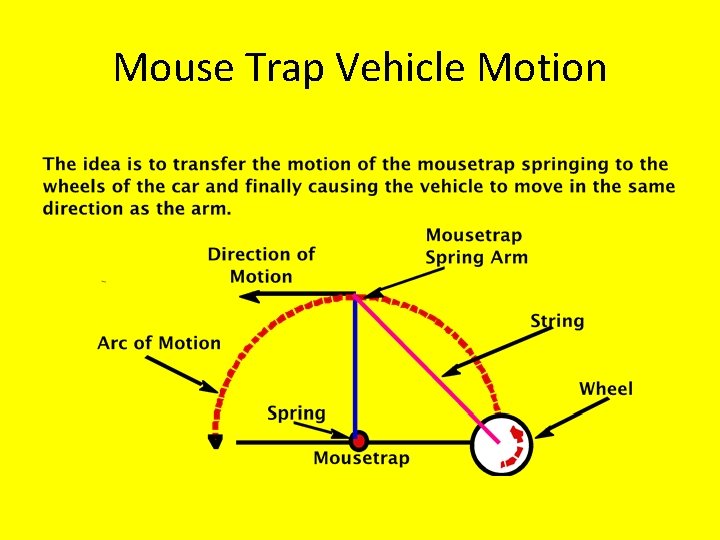
Mouse Trap Vehicle Motion

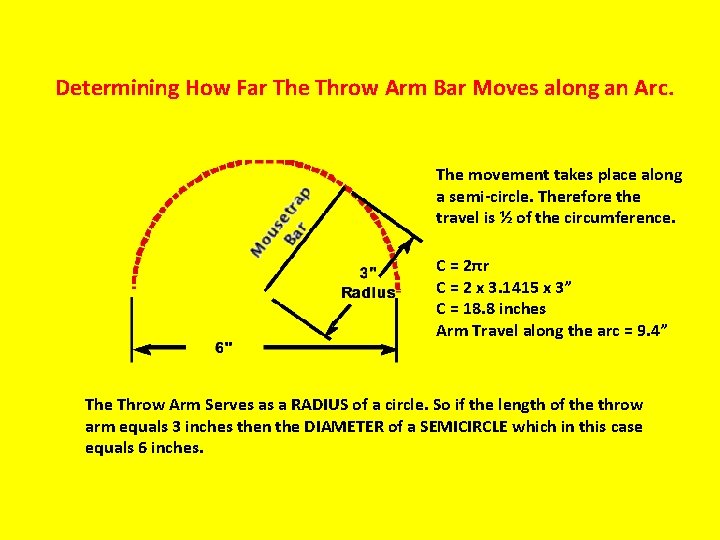
Determining How Far The Throw Arm Bar Moves along an Arc. The movement takes place along a semi-circle. Therefore the travel is ½ of the circumference. C = 2πr C = 2 x 3. 1415 x 3” C = 18. 8 inches Arm Travel along the arc = 9. 4” The Throw Arm Serves as a RADIUS of a circle. So if the length of the throw arm equals 3 inches then the DIAMETER of a SEMICIRCLE which in this case equals 6 inches.

Forces [1] • Loading the trap – Pull the mousetrap using a spring scale and observe the reading at certain points on arm. – Using distance of travel for the bar • Measure the angle using a protractor • Use geometry (Angle/360) (2πr) – Calculate spring constant, k • F= kx

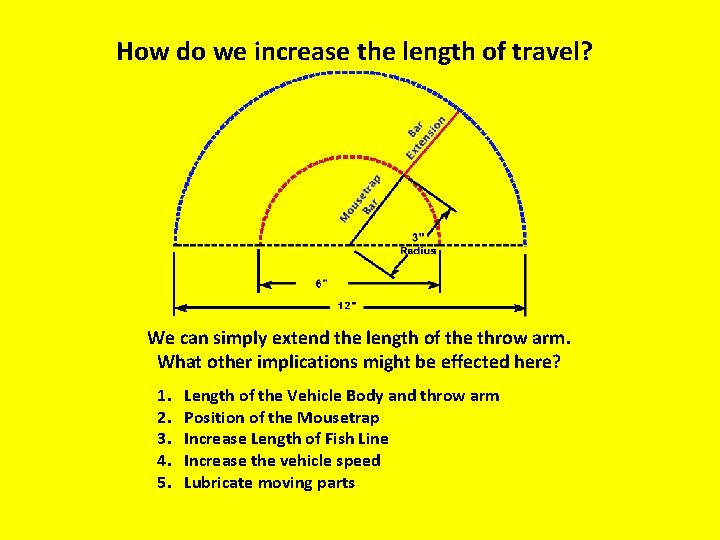
How do we increase the length of travel? We can simply extend the length of the throw arm. What other implications might be effected here? 1. 2. 3. 4. 5. Length of the Vehicle Body and throw arm Position of the Mousetrap Increase Length of Fish Line Increase the vehicle speed Lubricate moving parts

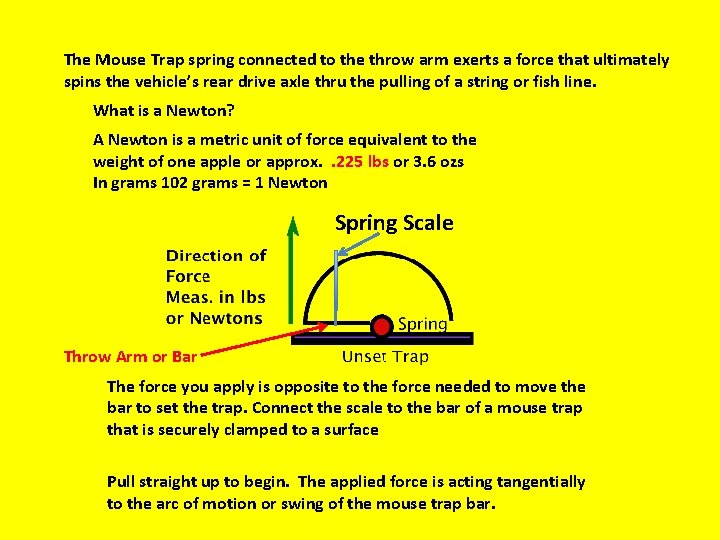
The Mouse Trap spring connected to the throw arm exerts a force that ultimately spins the vehicle’s rear drive axle thru the pulling of a string or fish line. What is a Newton? A Newton is a metric unit of force equivalent to the weight of one apple or approx. . 225 lbs or 3. 6 ozs In grams 102 grams = 1 Newton Spring Scale Throw Arm or Bar The force you apply is opposite to the force needed to move the bar to set the trap. Connect the scale to the bar of a mouse trap that is securely clamped to a surface Pull straight up to begin. The applied force is acting tangentially to the arc of motion or swing of the mouse trap bar.

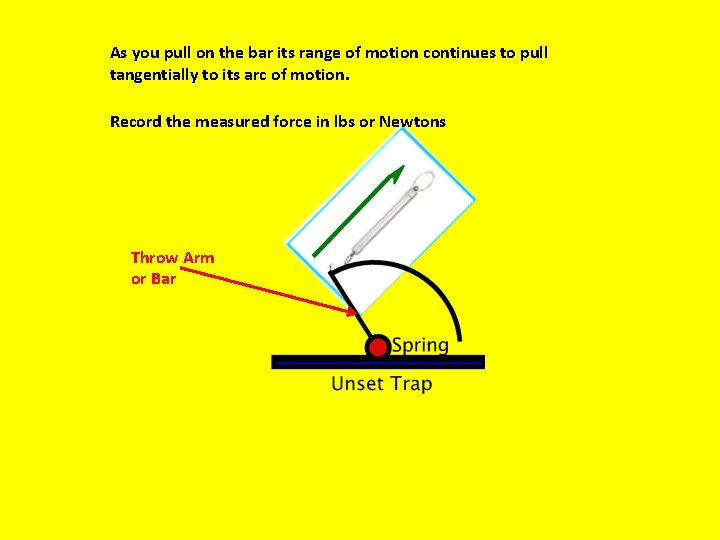
As you pull on the bar its range of motion continues to pull tangentially to its arc of motion. Record the measured force in lbs or Newtons Throw Arm or Bar

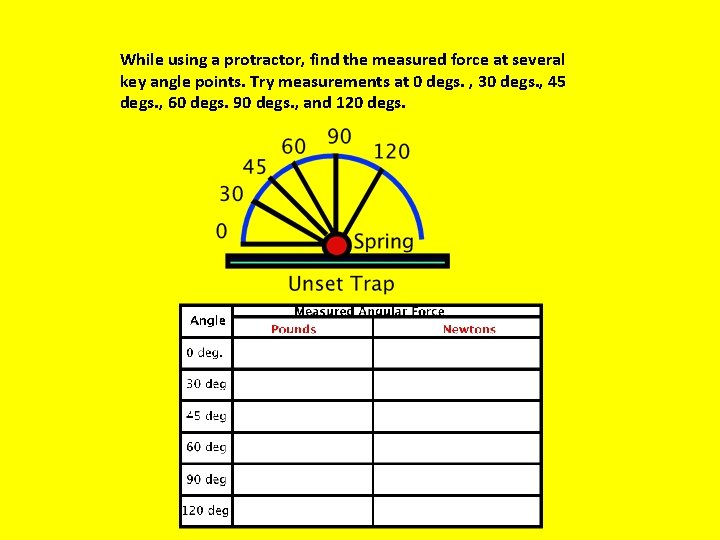
While using a protractor, find the measured force at several key angle points. Try measurements at 0 degs. , 30 degs. , 45 degs. , 60 degs. 90 degs. , and 120 degs.

Forces [2] Force 1 • Introduce vectors F t l su Re t an Force 2 e c or

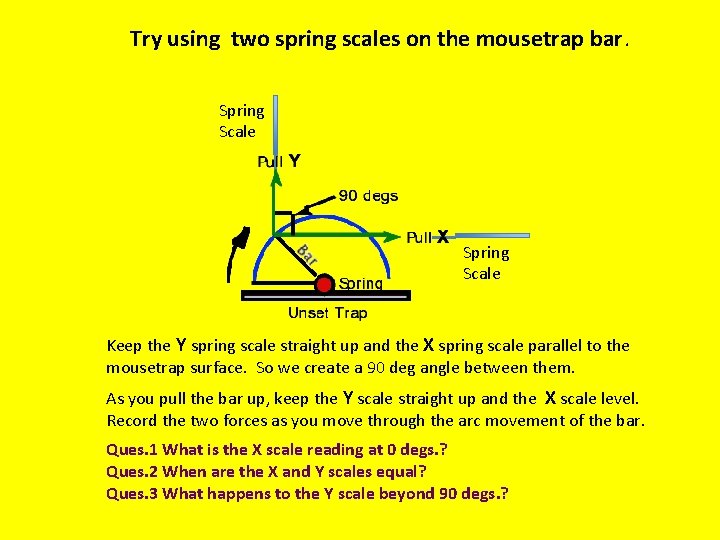
Try using two spring scales on the mousetrap bar. Spring Scale Keep the Y spring scale straight up and the X spring scale parallel to the mousetrap surface. So we create a 90 deg angle between them. As you pull the bar up, keep the Y scale straight up and the X scale level. Record the two forces as you move through the arc movement of the bar. Ques. 1 What is the X scale reading at 0 degs. ? Ques. 2 When are the X and Y scales equal? Ques. 3 What happens to the Y scale beyond 90 degs. ?

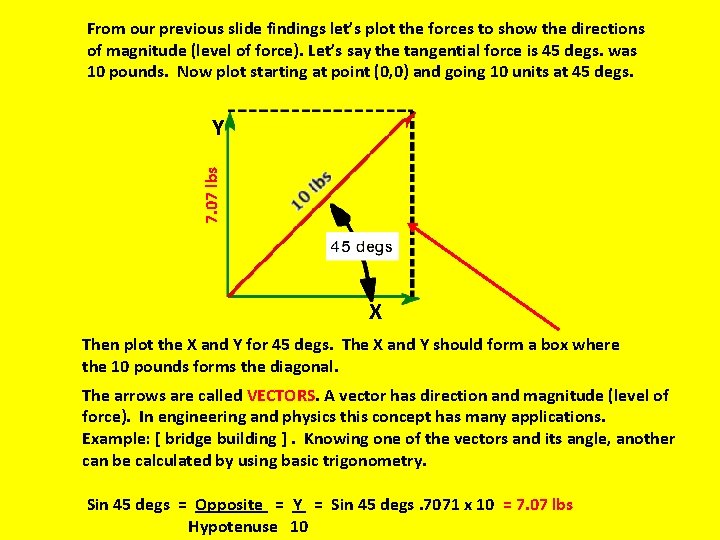
From our previous slide findings let’s plot the forces to show the directions of magnitude (level of force). Let’s say the tangential force is 45 degs. was 10 pounds. Now plot starting at point (0, 0) and going 10 units at 45 degs. 7. 07 lbs Y X Then plot the X and Y for 45 degs. The X and Y should form a box where the 10 pounds forms the diagonal. The arrows are called VECTORS. A vector has direction and magnitude (level of force). In engineering and physics this concept has many applications. Example: [ bridge building ]. Knowing one of the vectors and its angle, another can be calculated by using basic trigonometry. Sin 45 degs = Opposite = Y = Sin 45 degs. 7071 x 10 = 7. 07 lbs Hypotenuse 10

Math/Physics • Axle Diameter Table and Question • Wheel Diameter Table

Determining Rotational Speed with Axle Diameter

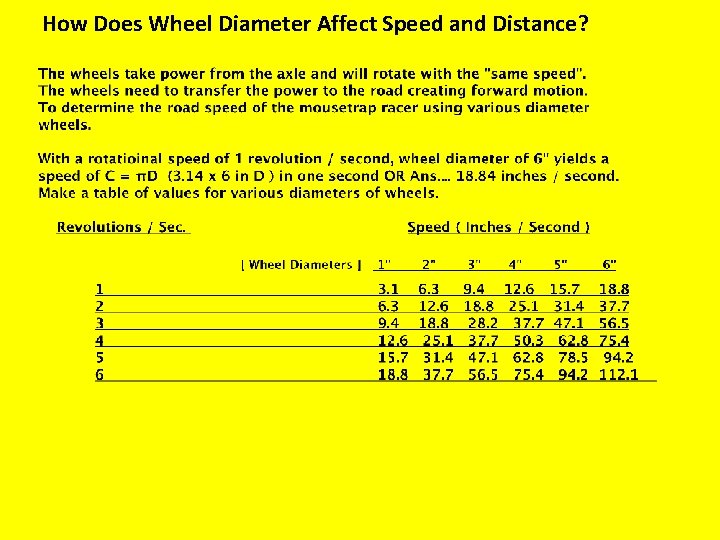
How Does Wheel Diameter Affect Speed and Distance?

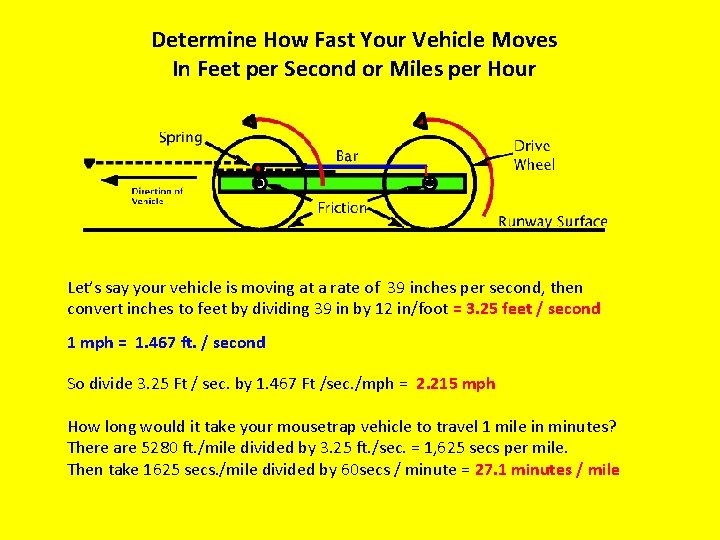
Determine How Fast Your Vehicle Moves In Feet per Second or Miles per Hour Let’s say your vehicle is moving at a rate of 39 inches per second, then convert inches to feet by dividing 39 in by 12 in/foot = 3. 25 feet / second 1 mph = 1. 467 ft. / second So divide 3. 25 Ft / sec. by 1. 467 Ft /sec. /mph = 2. 215 mph How long would it take your mousetrap vehicle to travel 1 mile in minutes? There are 5280 ft. /mile divided by 3. 25 ft. /sec. = 1, 625 secs per mile. Then take 1625 secs. /mile divided by 60 secs / minute = 27. 1 minutes / mile

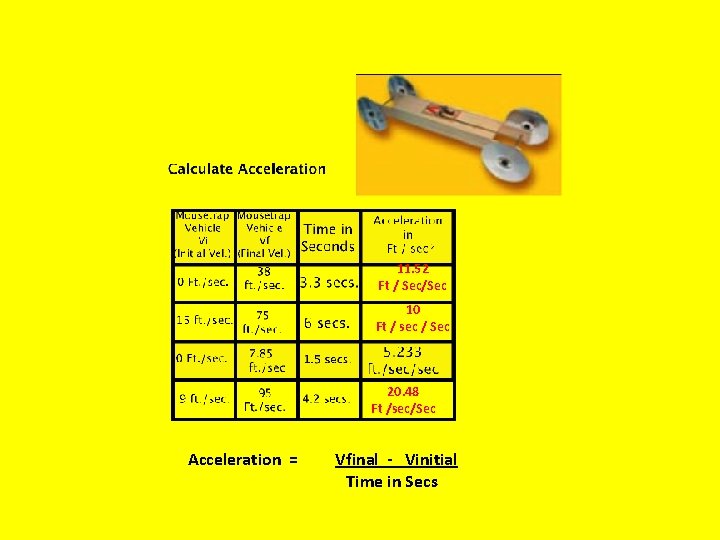
11. 52 Ft / Sec/Sec 10 Ft / sec / Sec 20. 48 Ft /sec/Sec Acceleration = Vfinal - Vinitial Time in Secs

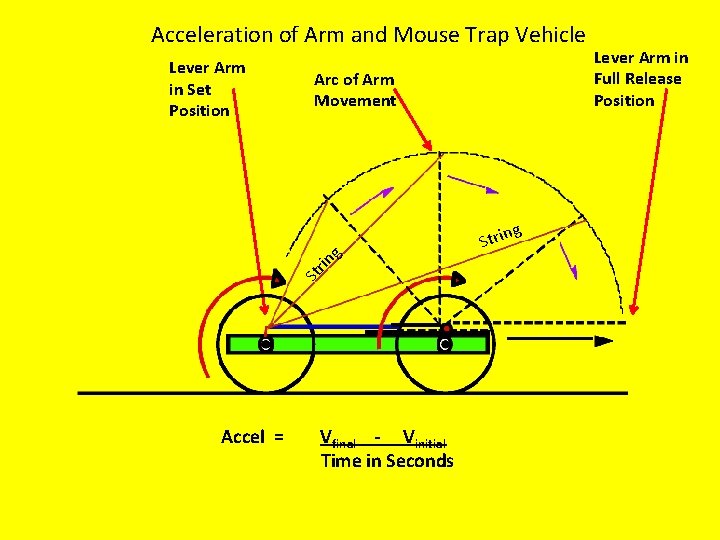
Acceleration of Arm and Mouse Trap Vehicle Lever Arm in Set Position Arc of Arm Movement g St ri ng Strin Accel = Vfinal - Vinitial Time in Seconds Lever Arm in Full Release Position

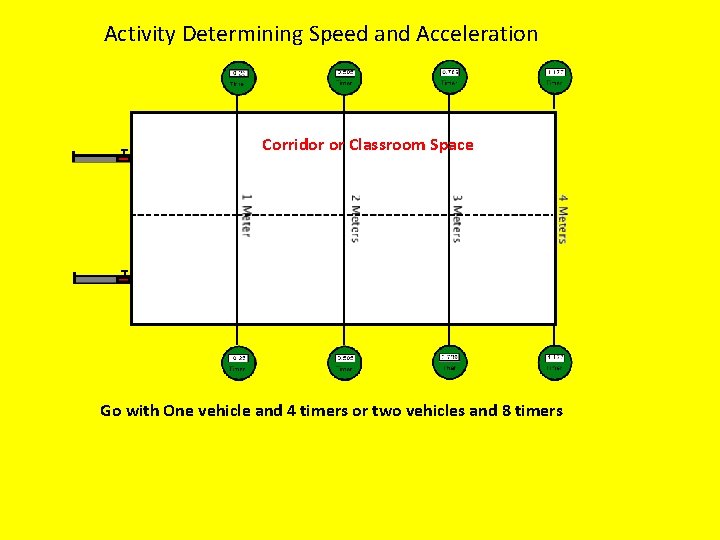
Activity Determining Speed and Acceleration Corridor or Classroom Space Go with One vehicle and 4 timers or two vehicles and 8 timers

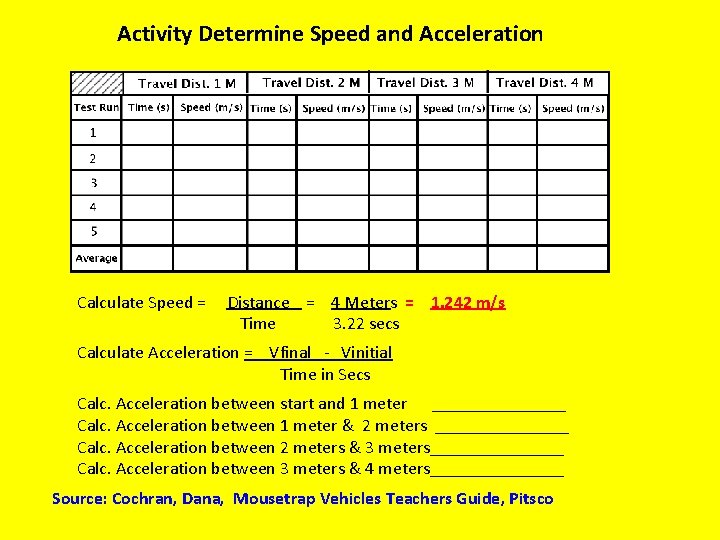
Activity Determine Speed and Acceleration Calculate Speed = Distance = 4 Meters = 1. 242 m/s Time 3. 22 secs Calculate Acceleration = Vfinal - Vinitial Time in Secs Calc. Acceleration between start and 1 meter ________ Calc. Acceleration between 1 meter & 2 meters ________ Calc. Acceleration between 2 meters & 3 meters________ Calc. Acceleration between 3 meters & 4 meters________ Source: Cochran, Dana, Mousetrap Vehicles Teachers Guide, Pitsco

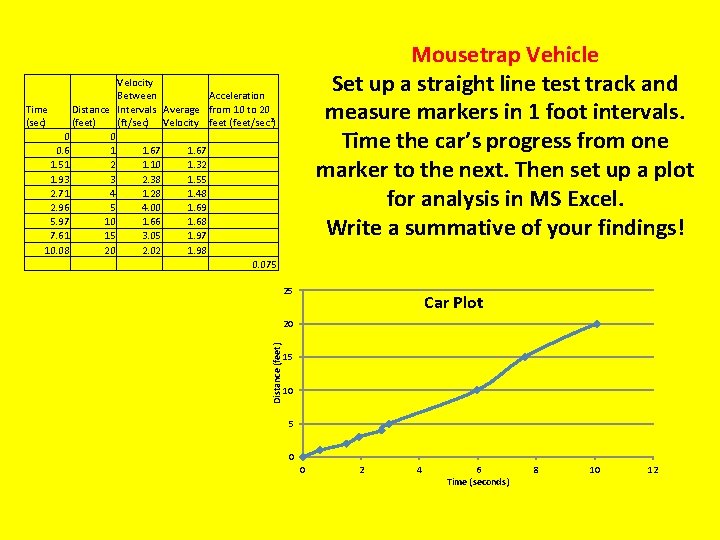
Mousetrap Vehicle Set up a straight line test track and measure markers in 1 foot intervals. Time the car’s progress from one marker to the next. Then set up a plot for analysis in MS Excel. Write a summative of your findings! Velocity Acceleration Between Time Distance Intervals Average from 10 to 20 (sec) (feet) (ft/sec) Velocity feet (feet/sec 2) 0 0 0. 6 1 1. 67 1. 51 2 1. 10 1. 32 1. 93 3 2. 38 1. 55 2. 71 4 1. 28 1. 48 2. 96 5 4. 00 1. 69 5. 97 10 1. 66 1. 68 7. 61 15 3. 05 1. 97 10. 08 20 2. 02 1. 98 0. 075 25 Car Plot Distance (feet) 20 15 10 5 0 0 2 4 6 Time (seconds) 8 10 12

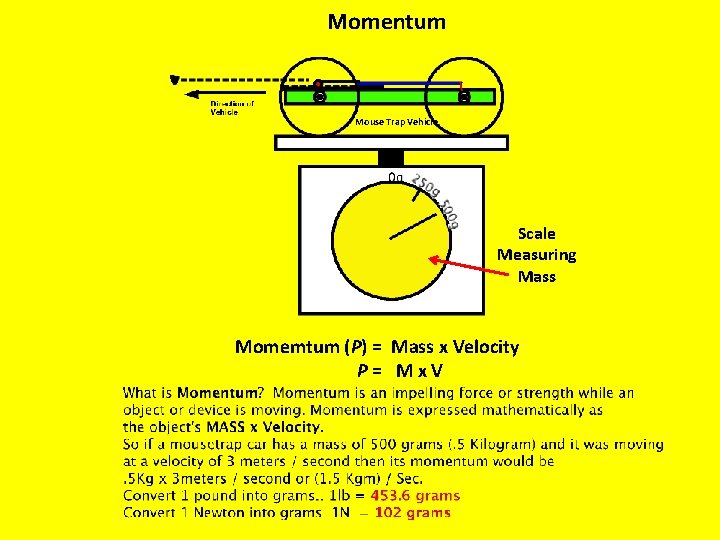
The Big Mo • Momentum = Mass x Velocity • P = M x V

Momentum Mouse Trap Vehicle Scale Measuring Mass Momemtum (P) = Mass x Velocity P= Mx. V

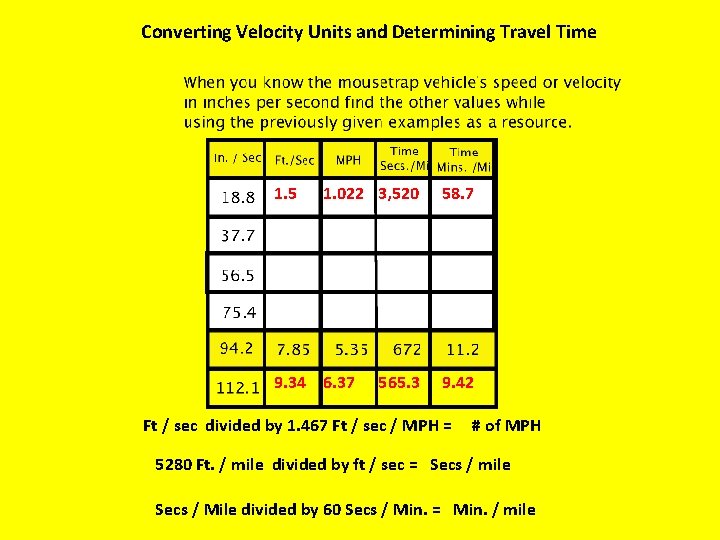
Converting Velocity Units and Determining Travel Time 1. 5 1. 022 3, 520 9. 34 6. 37 565. 3 58. 7 9. 42 Ft / sec divided by 1. 467 Ft / sec / MPH = # of MPH 5280 Ft. / mile divided by ft / sec = Secs / mile Secs / Mile divided by 60 Secs / Min. = Min. / mile

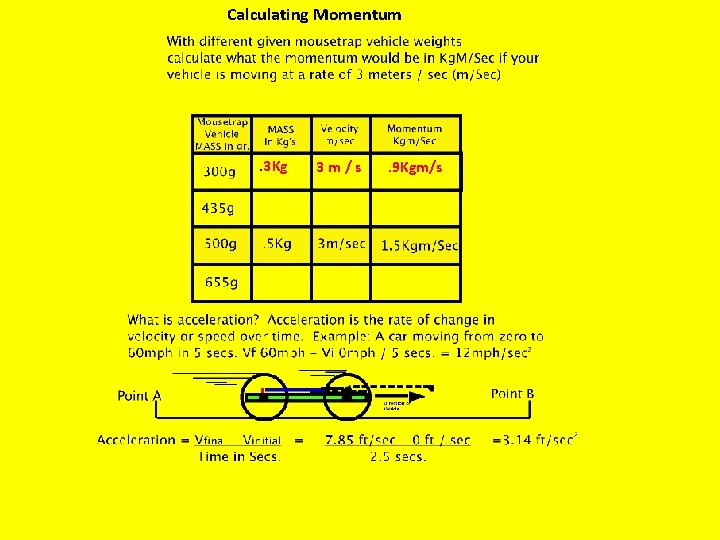
Calculating Momentum . 3 Kg 3 m/s . 9 Kgm/s

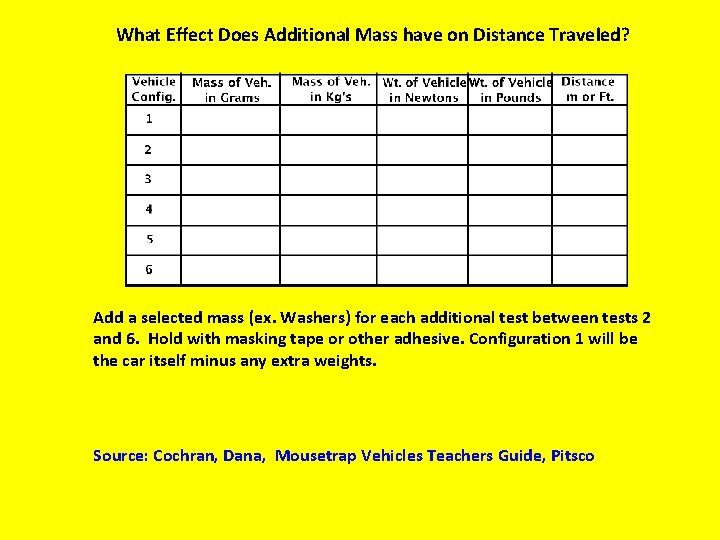
What Effect Does Additional Mass have on Distance Traveled? Add a selected mass (ex. Washers) for each additional test between tests 2 and 6. Hold with masking tape or other adhesive. Configuration 1 will be the car itself minus any extra weights. Source: Cochran, Dana, Mousetrap Vehicles Teachers Guide, Pitsco

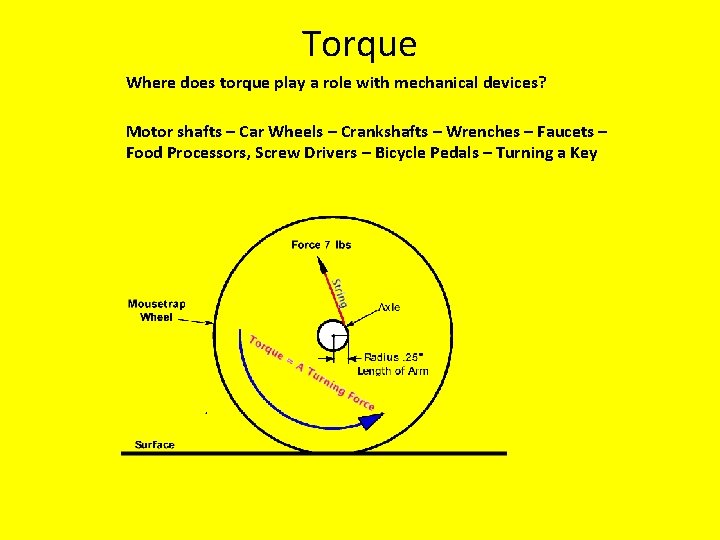
Torque Where does torque play a role with mechanical devices? Motor shafts – Car Wheels – Crankshafts – Wrenches – Faucets – Food Processors, Screw Drivers – Bicycle Pedals – Turning a Key

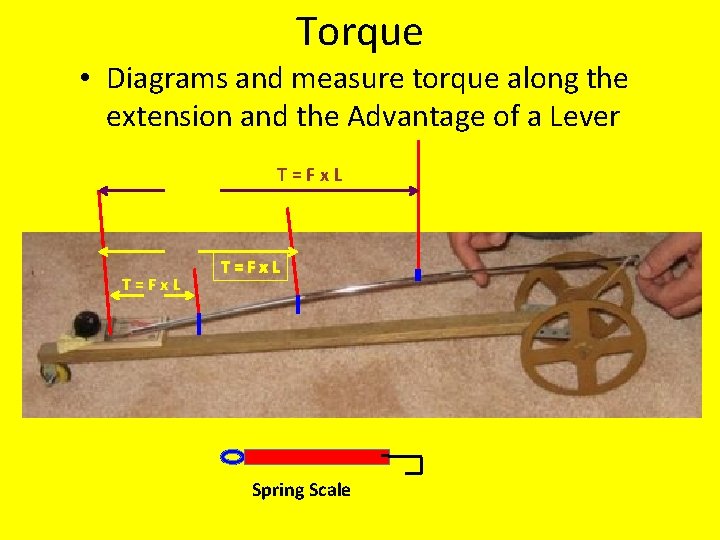
Torque • Diagrams and measure torque along the extension and the Advantage of a Lever T=Fx. L Spring Scale

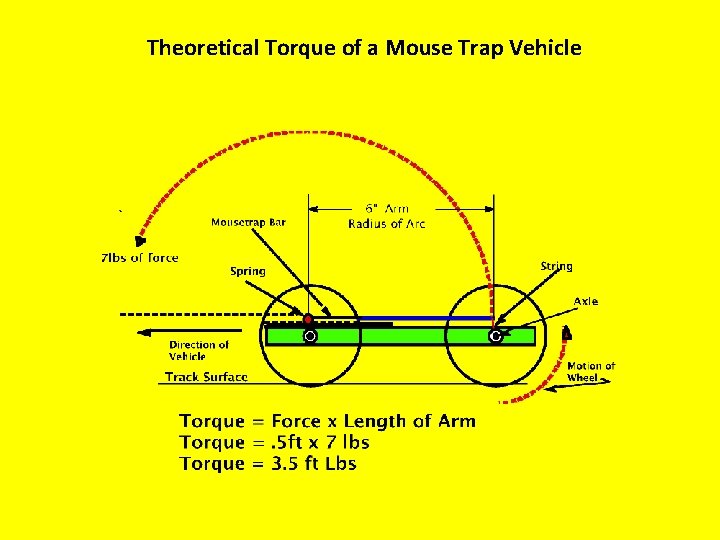
Theoretical Torque of a Mouse Trap Vehicle

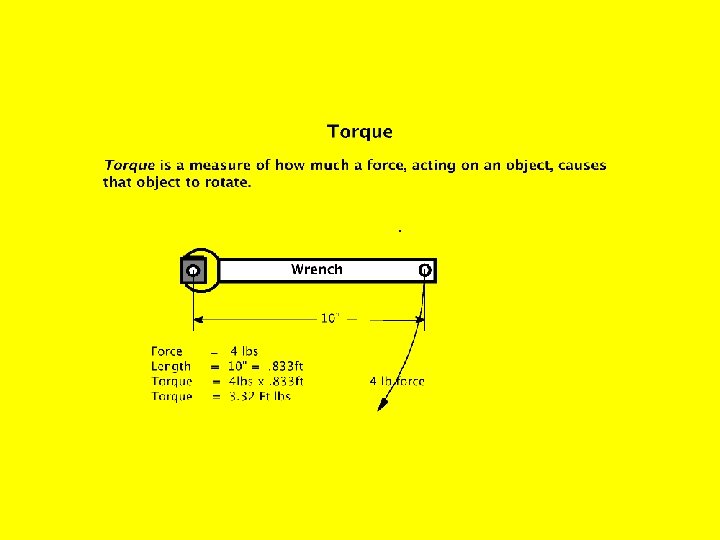
Torsion Wheel For Measuring Force of Trap Spring Torque by definition is a force that produces rotation Springs that store energy are called Torsion Springs Torque = Force x Radius OR Force x Length of Arm Radius of Mouse Trap Spring =. 1465 in. Force to lift and turn spring = 8 Newtons or 1. 8 lbs. 1 Newton =. 225 lbs Thus 8 N x. 225 lbs = 1. 8 lbs Torque = Force x Radius T= 1. 8 lb x. 1465 in T=. 265 in lbs

Friction • Coefficient of Friction – Static Friction - Fs – Kinetic Friction - Fk – Rolling Friction - Fr • Another example – Box

Friction and the Coefficient of Friction Happens! Friction is a “Force” brought on by two surfaces or materials rubbing against each other, that slows motion, reduces energy efficiency and has an outcome of heat losses. Static Friction = Fs and is normally greater than Kinetic Friction (Fk) Kinetic Friction= Fk and is normally less than Static Friction (Fs) Rolling Friction = Fr is less than Kinetic Friction ( Fk ) Coefficient of Friction Formula µ = Applied Force Normal Force

Friction Coefficient 20 lbs 80 lbs Coefficient of Friction µ = Applied Force Normal Force Coefficient of Friction µ = 20 lbs =. 25 80 lbs

Friction Coefficient 65 N 175 N Coefficient of Friction µ = Applied Force Normal Force Coefficient of Friction µ = 65 N 175 N =. 371

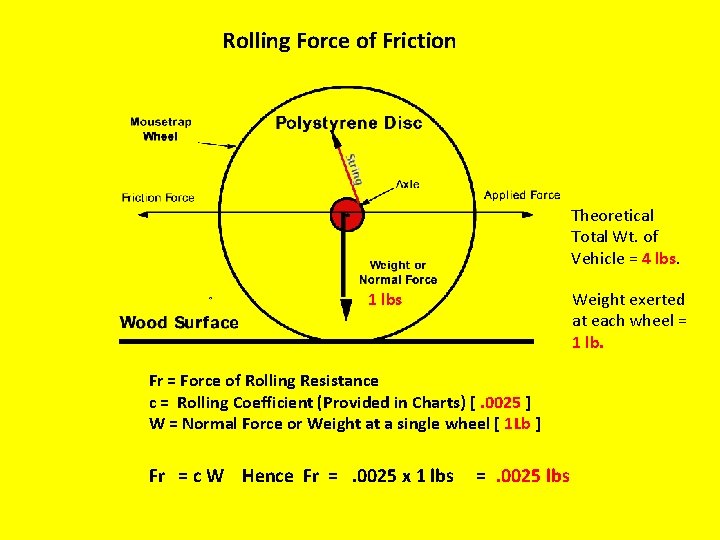
Rolling Force of Friction Theoretical Total Wt. of Vehicle = 4 lbs. 1 lbs Weight exerted at each wheel = 1 lb. Fr = Force of Rolling Resistance c = Rolling Coefficient (Provided in Charts) [. 0025 ] W = Normal Force or Weight at a single wheel [ 1 Lb ] Fr = c W Hence Fr =. 0025 x 1 lbs =. 0025 lbs

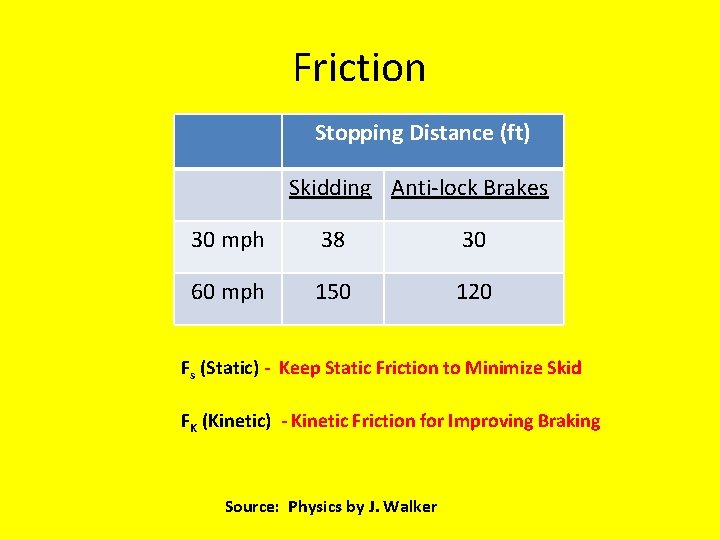
Friction Stopping Distance (ft) Skidding Anti-lock Brakes 30 mph 38 30 60 mph 150 120 Fs (Static) - Keep Static Friction to Minimize Skid FK (Kinetic) - Kinetic Friction for Improving Braking Source: Physics by J. Walker

Where Static Friction is Important Con Handicap Ramp veyo r Syst em

Where do you find Friction and Heat Losses in your Mousetrap Vehicle? FRICTION HAPPENS!! 1. Between Front Axle & Straw 2. Between Fish line and Rear Axle 3. Between Wheels and the Run Way Surface 4. Between Screw Eyes and Rear Axle 5. Between Torsion Spring Arm and Throw Arm 6. Between Throw Arm and the Torsion Spring’s Interior

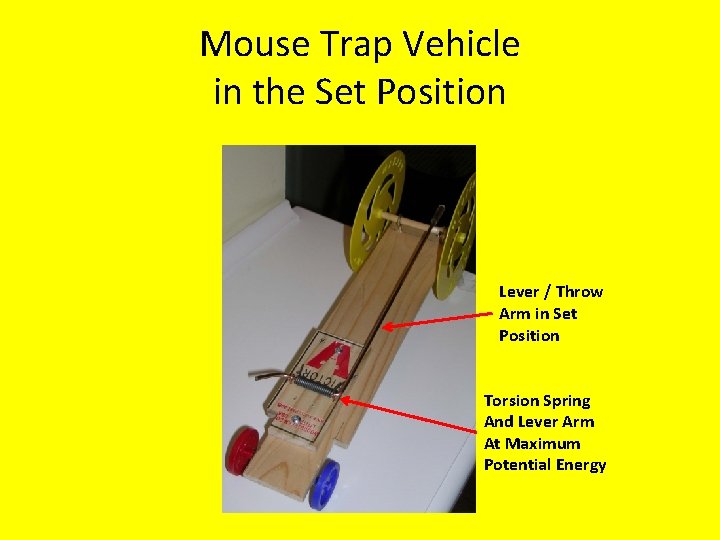
Mouse Trap Vehicle in the Set Position Lever / Throw Arm in Set Position Torsion Spring And Lever Arm At Maximum Potential Energy

Mouse Trap Vehicle Determining Mass / Weight 125. 1 gm = 1. 2255 N 125. 1 gm =. 267861 lb or 4. 29 oz 1 Newton = 102 Grams / 1 Lb = 453. 6 gm / 1 lb = 4. 45 N

Mousetrap Vehicle Questions That We Can Now Answer 1. What is Momentum? How can momentum be calculated? 2. Explain what is the Coefficient of Friction? 3. What is Torque? How do you calculate Torque? 4. How do you determine acceleration mathematically with final and initial velocity? 5. How can you determine Speed when you know distance and time? 6. What design modifications can control the distance the vehicle moves? 7. Does Mass effect how far a vehicle can travel? 8. What are the units for mass vs the units for weight? 9. What can you do to make your vehicle go faster? 10. How does wheel diameter affect speed and distance?

Questions, Answers, Suggestions? Chuck Goodwin, DTE Endicott, New York cgnystea@stny. rr. com Mouse Trap Vehicles ROCK!

Moustrap Video Trip • • • Distance Traveled = 27 feet Time of Travel = 6. 85 secs. Diameter of Driver Wheel = 4. 75 inches Solve for Circumference = πD Solve for Speed = Distance / Time (Ft/ Sec) Solve for Speed in MPH 1. 47 ft/Sec/mph Solve for Total Revolutions Completed Solve for Revs per Second Solve for Radians Covered Over Distance

Solve to Find Data Of An Actual Mouse. Trap Vehicle Run Circumference: = πD = 3. 14 x 4. 75 inches = How many feet in Wheel Circumference? Speed = Dist/Time = 27 ft / 6. 85 secs = Speed in Ft/Sec / 1. 47 Ft/Sec/mph = Revolutions Completed over 27 Ft How Many Revs. Per. Second? 3. 14 x 4. 75 In = 14. 915 in / 12 in/foot = 1. 243 ft. 3. 94 Ft / Sec 2. 68 MPH 27 Ft. / 1. 243 Ft / Rev = 21. 72 Revs / 6. 85 Secs = 3. 17 Revs/Sec. How Many Radians Completed over 27 Ft=. 21. 72 Revs x 6. 28 Rads / Rev = 136. 42 Rads