Program Linier Riset Operasi I Apakah Program Linier

Program Linier Riset Operasi I

Apakah Program Linier ? • Definisi : – Suatu model matematik yang berhubungan dengan alokasi yang efisien dari sumber yang terbatas untuk mencapai tujuan yang diinginkan (memaksimumkan keuntungan atau meminimumkan biaya) • Karakteristik dari Programa Linier : – Seluruh variabel adalah kontinu (dapat berbentuk nilai fraksional). – Tujuan (obyektif) nya tunggal (maximum atau minimum) – Fungsi Obyektif dan Pembatas adalah fungsi linier

Penerapan Program Linier • • Work scheduling Production planning & Production process Capital budgeting Financial planning Blending (Mis: Oil refinery management) Farm planning Distribution Multi-period decision problems – Inventory model – Financial models – Work scheduling

Model Programa Linier Maksimasi atau Minimasi : x 0 = c 1 x 1 + c 2 x 2 +. . . + cnxn Fungsi a 11 x 1 + a 12 x 2 +. . . + a 1 nxn ( , =, atau ) b 1 Pembatas a 21 x 1 + a 22 x 2 +. . . + a 2 nxn ( , =, atau ) b 2. . . am 1 x 1 + am 2 x 2 +. . . + amnxn ( , =, atau ) bm x 1, x 2, …. , xn 0

Bentuk Kanonik Program Linier Maksimasi Semua variabel keputusan adalah non-negatif (xj) Fungsi obyektifnya adalah tipe maksimasi 1. Semua pembatas mempunyai tipe

Asumsi Dasar Pada Program Linier • Proporsional. – Kontribusi fungsi obyektif dari tiap variabel keputusan proporsional terhadap nilai variabel – Konstribusi tiap variabel keputusan terhadap sisi sebelah kiri tiap pembatas adalah proporsional terhadap nilai variabel keputusan.

Asumsi Dasar Pada Program Linier • Ketidaktergantungan – Konstribusi dari fungsi obyektif untuk setiap variabel keputusan tidak bergantung dari variabel keputusan lainnya. – Konstribusi dari suatu variabel keputusan terhadap sisi kiri tiap batasan tidak bergantung dari nilai-nilai dari variabel keputusan lainnya.

Asumsi Dasar Pada Program Linier • Dapat Dibagi. – Tiap variabel keputusan diperbolehkan bernilai pecahan. Jika tidak, maka harus menggunakan Integer Programming (IP). • Tertentu. – Tiap parameter diketahui dengan pasti.

Tranformasi Permasalahan Program Linier (1) Lima cara mentranformasi permasalahan program linier – Fungsi Minimasi, x 0 sama dengan g 0 = - x 0 maksimasi dari Minimasi x 0 = c 1 x 1 + c 2 x 2 +. . . + cnxn Sama dengan Maksimasi g 0 = -x 0 = - c 1 x 1 - c 2 x 2 -. . . - cnxn

Tranformasi Permasalahan Program Linier (2) • Ketidaksamaan pada satu arah ( , atau ) dapat diubah menjadi ketidaksamaan pada arah berlawanan ( , atau ) • Contoh : a 1 x 1 + a 2 x 2 b ekuivalen dengan - a 1 x 1 - a 2 x 2 -b Atau a 1 x 1 + a 2 x 2 b ekuivalen dengan - a 1 x 1 - a 2 x 2 -b

Tranformasi Permasalahan Program Linier (3) • Bila fungsi pembatas dalam bentuk persamaan dapat diubah menjadi dua bentuk ketidaksamaan. • Contoh : a 1 x 1 + a 2 x 2 = b menjadi a 1 x 1 + a 2 x 2 b dan Atau a 1 x 1 + a 2 x 2 b dan a 1 x 1 + a 2 x 2 b - a 1 x 1 - a 2 x 2 -b

Tranformasi Permasalahan Program Linier (4) • Batasan dalam bentuk ketidaksamaan dengan ruas kiri bernilai absolut dapat diubah menjadi dua ketidaksamaan. • Contoh : | a 1 x 1 + a 2 x 2 | b untuk b 0 menjadi : a 1 x 1 + a 2 x 2 -b dan a 1 x 1 + a 2 x 2 b | a 1 x 1 + a 2 x 2 | b untuk b 0 menjadi : a 1 x 1 + a 2 x 2 b dan a 1 x 1 + a 2 x 2 -b

Transformasi Ketidaksamaan Persamaan • Untuk penyelesaian masalah programa linier, pembatas yang berbentuk ketidaksamaan harus dirubah menjadi persamaan. • Bila bentuk ketidaksamaannya adalah , untuk menjadi persamaan harus dikurangi sebesar S, biasanya disebut surplus variabel. • Bila bentuk ketidaksamaannya adalah , untuk menjadi persamaan harus ditambah sebesar S, biasanya disebut slack variabel.

Contoh : Maksimasi : x 0 = x 1 - 3 x 2 Fungsi Pembatas menjadi Fungsi Pembatas : - x 1 + 2 x 2 5 - x 1 + 2 x 2 + S 1 = 5 x 1 + 3 x 2 10 x 1 + 3 x 2 - S 2 = 10 x 1, x 2 0 Bila Fungsi Pembatas menjadi Fungsi = 5 Pembatas : - x 1 + 2 x 2 5 - x 1 + 2 x 2 + S 1 x 1 + 3 x 2 10 x 1 + 3 x 2 - S 2 = 10 | 5 x 1 + 2 x 2 | 25 5 x + 2 x + S 3 = 25 1 2 x 1, x 2 0 5 x 1 + 2 x 2 - S 4 = -25

Metoda Penyelesain Program Linier Dua metoda digunakan untuk penyelesaian programa linier, yaitu : – Metoda Grafik. (Khusus untuk 2 variabel) Metoda penyelesaian permasalahan programa linier dengan jumlah variabel tidak lebih dari dua dengan menggambarkan secara grafis. – Metoda Simplex. Metoda penyelesaian programa linier secara aljabar dengan menggunakan bentuk persamaan standard. Jumlah variabelnya tidak dibatasi.

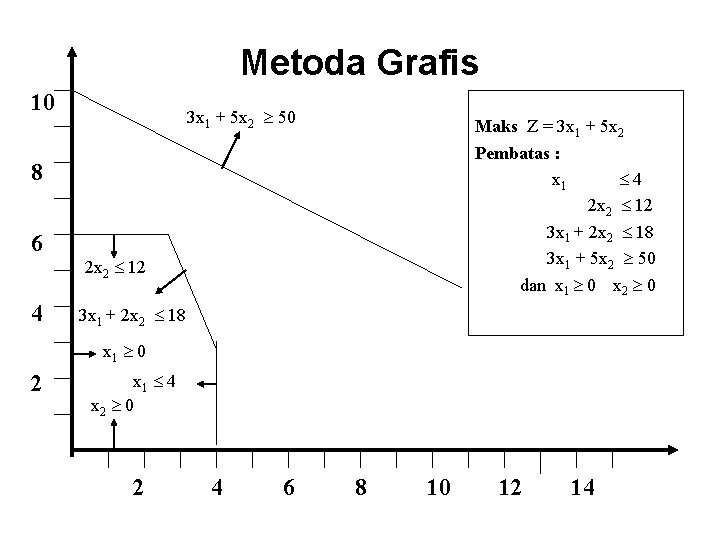
Metoda Grafis 10 3 x 1 + 5 x 2 50 Maks Z = 3 x 1 + 5 x 2 Pembatas : x 1 4 2 x 2 12 3 x 1 + 2 x 2 18 3 x 1 + 5 x 2 50 dan x 1 0 x 2 0 8 6 4 2 x 2 12 3 x 1 + 2 x 2 18 x 1 0 2 x 1 4 x 2 0 2 4 6 8 10 12 14

Terminologi Solusi Secara Grafis • Feasible Solution : Suatu solusi yang memenuhi semua fungsi yang ada pada batasan dari permasalahan. • Infeasible solution : Suatu solusi yang mempunyai paling sedikit satu fungsi tidak memenuhi batasan permasalahan. • Feasible region : Kumpulan dari semua ‘feasible solution’. Ada kemungkinan permasalahan yang tidak mempunyai satupun ‘feasible solution’.

Terminologi Solusi Secara Grafis (Lanjutan) • Optimal Solution : Suatu ‘feasible solution’ yang mempunyai nilai yang paling baik untuk fungsi tujuan. • Nilai Yang Paling Baik (Most Favourable Value) : Nilai terbesar bila fungsi obyektifnya Maksimum atau terkecil bila fungsi obyektifnya terkecil. • Multiple Optimal Solution : Suatu solusi dengan nilai optimal yang sama untuk kombinasi nilai variabel dari fungsi obyektif yang berbeda-beda.

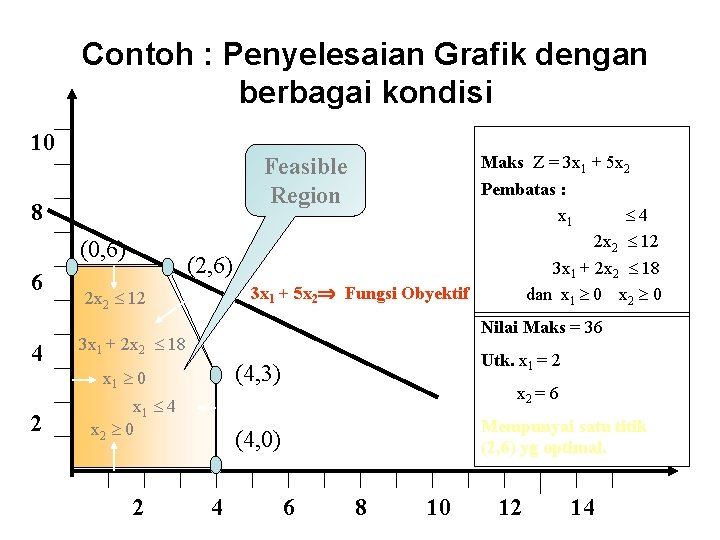
Contoh : Penyelesaian Grafik dengan berbagai kondisi 10 8 (0, 6) 6 4 2 Maks Z = 3 x 1 + 5 x 2 Pembatas : x 1 4 2 x 2 12 3 x 1 + 2 x 2 18 3 x 1 + 5 x 2 Fungsi Obyektif dan x 1 0 x 2 0 Feasible Region (2, 6) 2 x 2 12 Nilai Maks = 36 3 x 1 + 2 x 2 18 (4, 3) x 1 0 x 1 4 x 2 0 2 Utk. x 1 = 2 x 2 = 6 Mempunyai satu titik (2, 6) yg optimal. (4, 0) 4 6 8 10 12 14

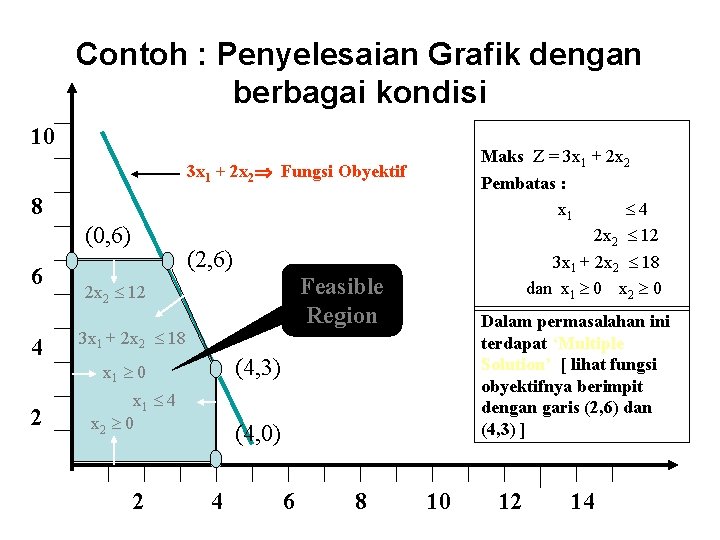
Contoh : Penyelesaian Grafik dengan berbagai kondisi 10 Maks Z = 3 x 1 + 2 x 2 Pembatas : x 1 4 2 x 2 12 3 x 1 + 2 x 2 18 dan x 1 0 x 2 0 3 x 1 + 2 x 2 Fungsi Obyektif 8 (0, 6) 6 (2, 6) Feasible Region 2 x 2 12 4 3 x 1 + 2 x 2 18 2 x 1 4 x 2 0 (4, 3) x 1 0 2 Dalam permasalahan ini terdapat ‘Multiple Solution’ [ lihat fungsi obyektifnya berimpit dengan garis (2, 6) dan (4, 3) ] (4, 0) 4 6 8 10 12 14

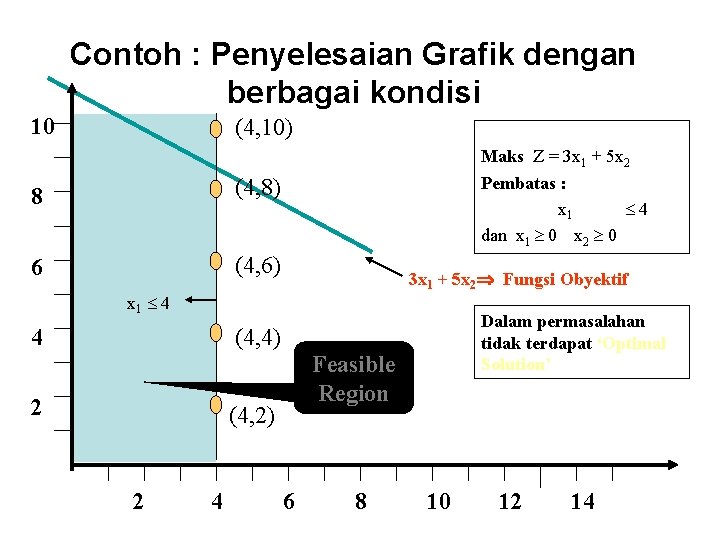
Contoh : Penyelesaian Grafik dengan berbagai kondisi 10 (4, 10) 8 (4, 8) 6 (4, 6) Maks Z = 3 x 1 + 5 x 2 Pembatas : x 1 4 dan x 1 0 x 2 0 3 x 1 + 5 x 2 Fungsi Obyektif x 1 4 Dalam permasalahan tidak terdapat ‘Optimal Solution’ (4, 4) 4 2 Feasible Region (4, 2) 2 4 6 8 10 12 14

1. 2. 3. 2 X 1 + X 2 ≥ 15 3 X 1 + 2 X 2 ≥ 10 X 1 ≥ 0 dan X 2 ≥ 0 1. 2. 3. 30 Xm + 20 Xk ≤ 300 5 Xm + 10 Xk ≤ 110 Xm ≥ 0 ; Xk ≥ 0 1. 2. 3. 4 XA + 6 XB ≥ 48 12 XA + 10 XB ≥ 120 XA ≥ 0 dan XB ≥ 0