RISET OPERASI METODE TRANSPORTASI Dosen Wawan Hari Subagyo

RISET OPERASI METODE TRANSPORTASI Dosen : Wawan Hari Subagyo

METODE TRANSPORTASI suatu metode yang digunakan untuk mengatur distribusi dari sumber-sumber yang menyediakan produk yang sama, ke tempat-tempat yang membutuhkan secara optimal Metode yang dipelajari : 1. Stepping Stone 2. Modi (Modified Distribution) 3. VAM (Vogel Aproximation Methode)

Metode Stepping-Stone Metode ini dalam merubah alokasi produk untuk mendapatkan alokasi produksi yang optimal menggunakan cara trial and error.

Metode Stepping-Stone Contoh : · Suatu perusahaan yang mempunyai 3 buah pabrik di W, H, P. Perusahaan menghadapi masalah alokasi hasil produksinya dari pabrik -pabrik tersebut ke gudang-gudang penjualan di A, B, C

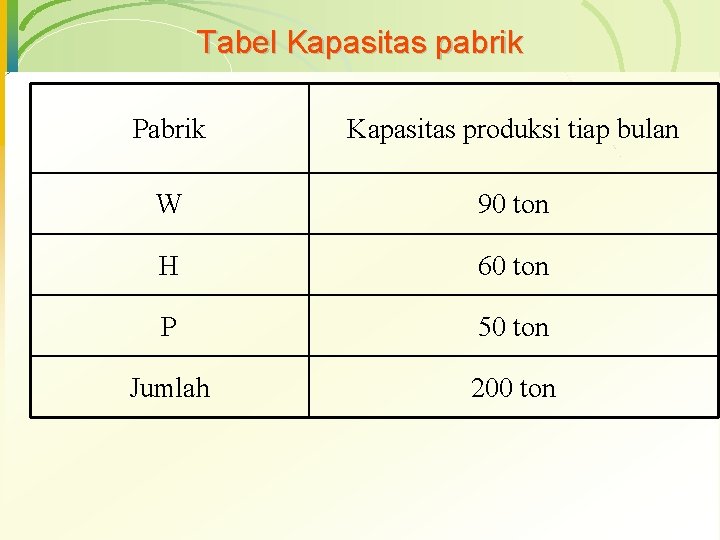
Tabel Kapasitas pabrik Pabrik Kapasitas produksi tiap bulan W 90 ton H 60 ton P 50 ton Jumlah 200 ton

Tabel Kebutuhan gudang Gudang Kebutuhan tiap bulan A 50 ton B 110 ton C 40 ton Jumlah 200 ton

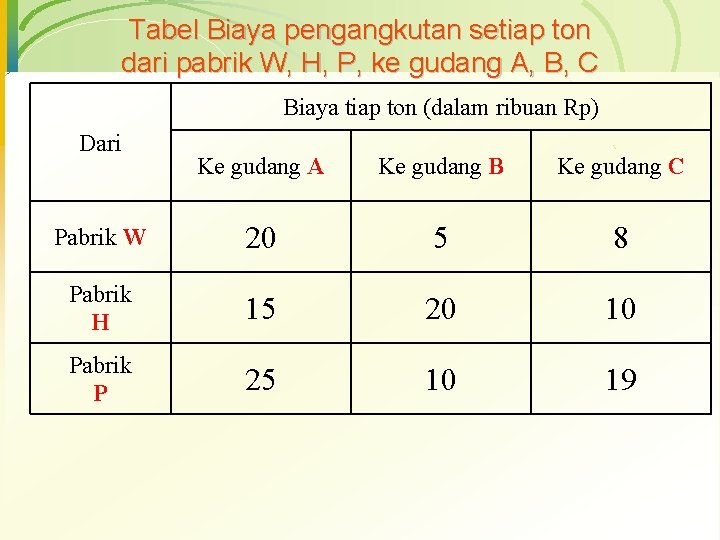
Tabel Biaya pengangkutan setiap ton dari pabrik W, H, P, ke gudang A, B, C Biaya tiap ton (dalam ribuan Rp) Dari Ke gudang A Ke gudang B Ke gudang C Pabrik W 20 5 8 Pabrik H 15 20 10 Pabrik P 25 10 19

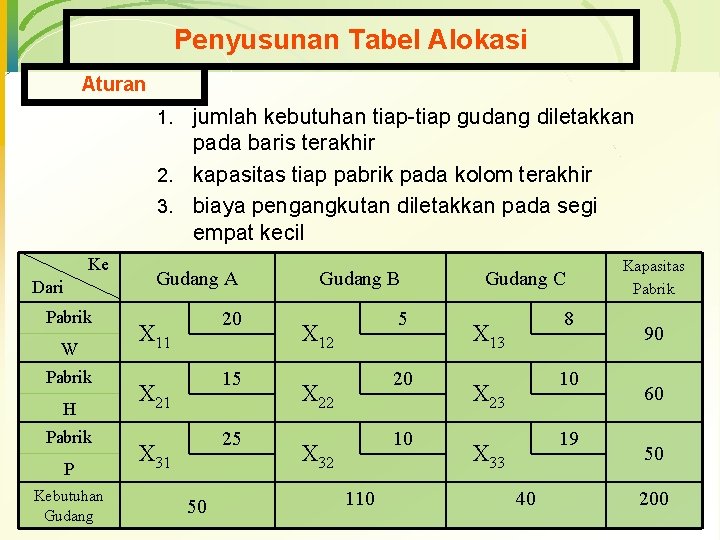
Penyusunan Tabel Alokasi Aturan jumlah kebutuhan tiap-tiap gudang diletakkan pada baris terakhir 2. kapasitas tiap pabrik pada kolom terakhir 3. biaya pengangkutan diletakkan pada segi empat kecil 1. Ke Dari Pabrik W Pabrik H Pabrik P Kebutuhan Gudang A 20 X 11 15 X 21 25 X 31 50 Gudang B 5 X 12 20 X 22 10 X 32 110 Gudang C 8 X 13 10 X 23 19 X 33 40 Kapasitas Pabrik 90 60 50 200

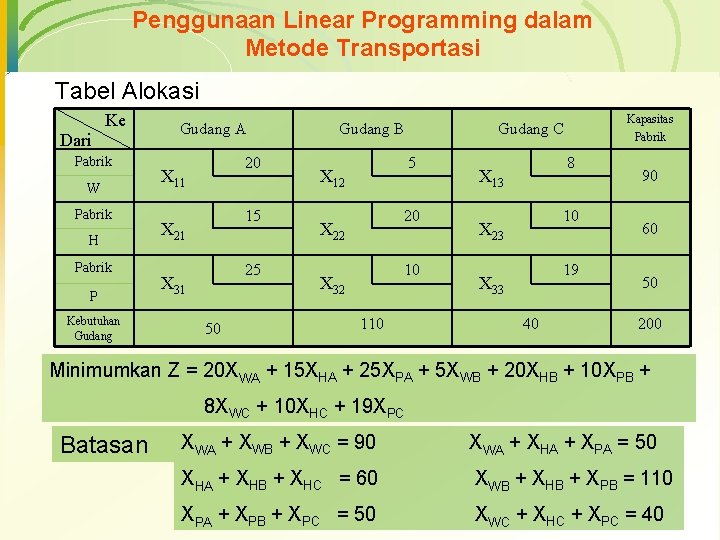
Penggunaan Linear Programming dalam Metode Transportasi Tabel Alokasi Dari Ke Pabrik W Pabrik H Pabrik P Kebutuhan Gudang A 20 X 11 15 X 21 25 X 31 50 Gudang B 5 X 12 20 X 22 10 X 32 110 Kapasitas Gudang C Pabrik 8 X 13 10 X 23 19 X 33 40 90 60 50 200 Minimumkan Z = 20 XWA + 15 XHA + 25 XPA + 5 XWB + 20 XHB + 10 XPB + 8 XWC + 10 XHC + 19 XPC Batasan XWA + XWB + XWC = 90 XWA + XHA + XPA = 50 XHA + XHB + XHC = 60 XWB + XHB + XPB = 110 XPA + XPB + XPC = 50 XWC + XHC + XPC = 40

Prosedur Alokasi Pedoman sudut barat laut (nortwest corner rule) yaitu pengalokasian sejumlah maksimum produk mulai dari sudut kiri atas (X 11) dengan melihat kapasitas pabrik dan kebutuhan gudang). 1. Mulai dari sudut kiri atas dari X 11 dialokasikan sejumlah maksimum produk dengan melihat kapasitas pabrik dan kebutuhan gudang 2. Setelah itu, bila Xij merupakan kotak terakhir yang dipilih dilanjutkan dengan mengalokasikan pada Xi, j+1 bila i mempunyai kapasitas yang tersisa 3. Bila tidak, alokasikan ke Xi+1, j, dan seterusnya sehingga semua kebutuhan telah terpenuhi

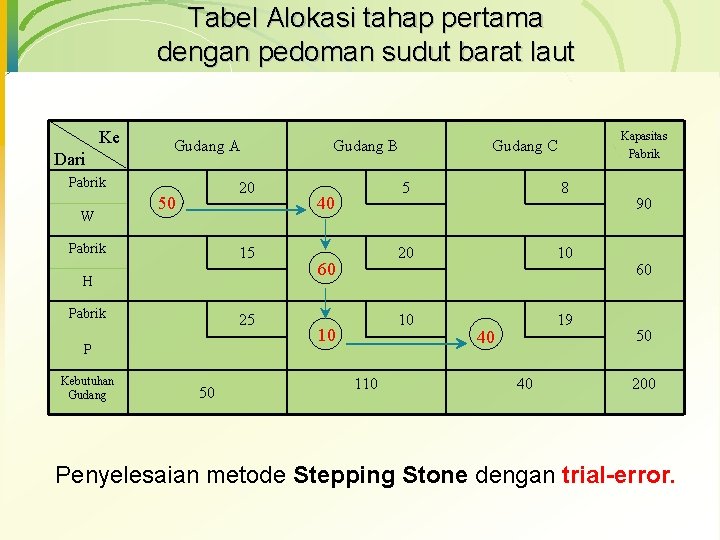
Tabel Alokasi tahap pertama dengan pedoman sudut barat laut Ke Dari Gudang A Pabrik W 20 50 Pabrik 15 H Pabrik 25 P Kebutuhan Gudang 50 Gudang B 40 60 10 110 Kapasitas Gudang C Pabrik 5 8 20 10 10 19 40 40 90 60 50 200 Penyelesaian metode Stepping Stone dengan trial-error.

Metode MODI (Modified Distribution) Formulasi Ri + Kj = Cij Ri = nilai baris i Kj = nilai kolom j C ij = biaya pengangkutan dari sumber i ke tujuan j

Metode MODI (Modified Distribution) Langkah Penyelesaian 1. Isilah tabel pertama dari sudut kiri atas ke kanan bawah 2. Menentukan nilai baris dan kolom dengan cara: • • Baris pertama selalu diberi nilai 0 Nilai baris yang lain dan nilai semua kolom ditentukan berdasarkan rumus Ri + Kj = Cij. Nilai baris W = RW = 0 Mencari nilai kolom A: RW + KA = CWA 0 + KA = 20, nilai kolom A = KA = 20 Mencari nilai kolom dan baris yg lain: RW + KB = CWB; 0 + KB = 5; KB = 5 RH + KB = CHB; RH + 5 = 20; RH = 15 RP + KB = CPB; RP + 5 = 10; RP = 5 RP + KC = CPC; 5 + KC = 19; KC = 14

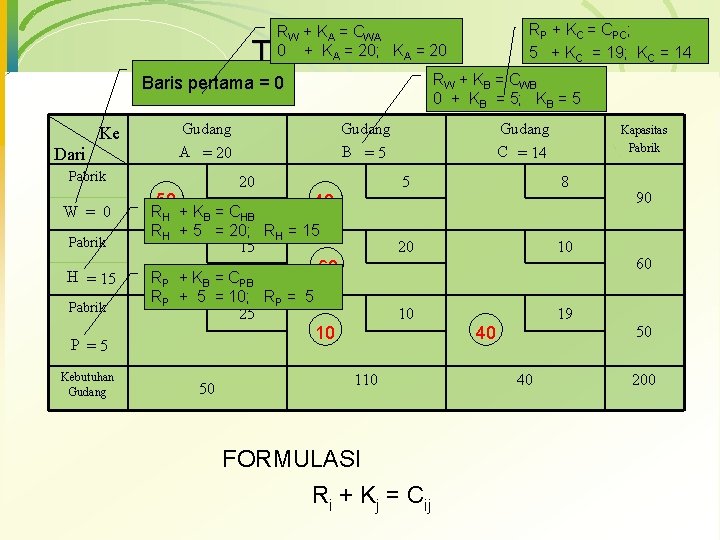
RP + KC = CPC; 5 + KC = 19; KC = 14 RW + KA = CWA 0 + KA = 20; KA = 20 Tabel Pertama RW + KB = CWB 0 + KB = 5; KB = 5 Baris pertama = 0 Gudang A = 20 Ke Dari Pabrik W = 0 Pabrik H = 15 Pabrik 20 50 40 RH + KB = CHB RH + 5 = 20; RH = 15 15 RP + KB = CPB RP + 5 = 10; RP = 5 25 P =5 Kebutuhan Gudang B =5 50 Gudang C = 14 Kapasitas Pabrik 5 8 20 10 10 19 60 10 110 FORMULASI Ri + Kj = Cij 40 40 90 60 50 200

3. Menghitung Indeks perbaikan adalah nilai dari segi empat air (segi empat yang kosong). Rumus : Cij - Ri - Kj = indeks perbaikan Tabel Indeks Perbaikan : Segi empat air Cij - Ri - Kj indeks perbaikan HA 15 – 15 - 20 -20 PA WC 25 – 20 8 – 0 – 14 0 -6 HC 10 – 15 – 14 -19

4. Memilih titik tolak perubahan Segi empat yang merupakan titik tolak perubahan adalah segi empat yang indeksnya bertanda negatif dan yang memenuhi syarat adalah segi empat HA dan dipilih sebagai segi empat yang akan diisi angkanya terbesar Segi empat air Cij - Ri - Kj indeks perbaikan HA 15 – 15 - 20 -20 PA 25 – 20 0 WC 8 – 0 – 14 -6 HC 10 – 15 – 14 -19

5. Memperbaiki alokasi 1. 2. 3. 4. Berikan tanda positif pada sel terpilih (HA) Pilihlah 1 sel terdekat yang mempunyai isi dan sebaris (HB), Pilihlah 1 sel terdekat yang mempunyai isi dan sekolom (WA); berilah tanda negatif keduanya Pilihlah 1 sel sebaris atau sekolom dengan 2 sel yang bertanda negatif tadi (WB), dan berilah sel ini tanda positif Pindahkanlah alokasi dari sel yang bertanda negatif ke yang bertanda positif sebanyak isi terkecil dari sel yang bertanda negatif (50) Jadi sel HA kemudian berisi 50, sel HB berisi 60 – 50 = 10, sel WB berisi 40 + 50 = 90, sel WA menjadi tidak berisi

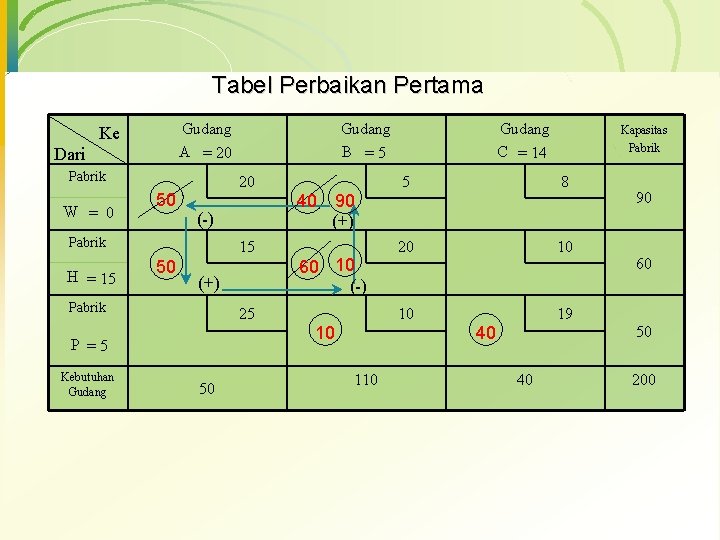
Tabel Perbaikan Pertama Gudang A = 20 Ke Dari Pabrik W = 0 50 20 (-) Pabrik H = 15 15 50 (+) Pabrik 25 P =5 Kebutuhan Gudang B =5 50 40 90 (+) 60 10 (-) 10 110 Gudang C = 14 Kapasitas Pabrik 5 8 20 10 10 19 40 40 90 60 50 200

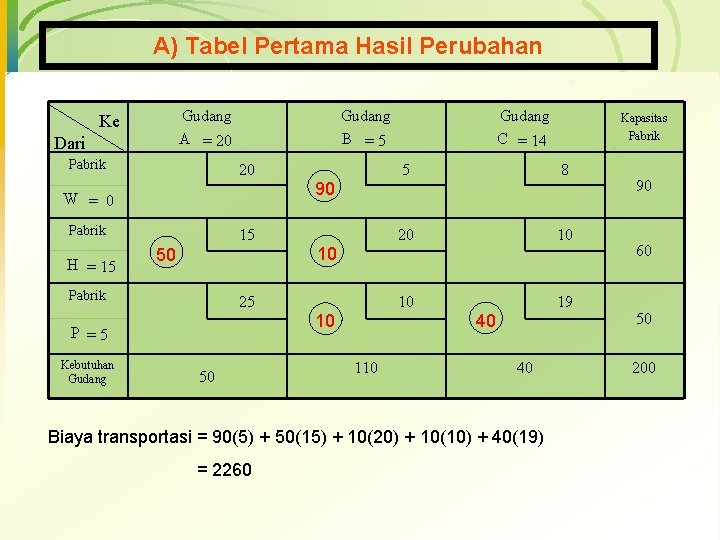
A) Tabel Pertama Hasil Perubahan Gudang A = 20 Ke Dari Pabrik Gudang B =5 20 Pabrik 15 50 Pabrik 10 25 10 P =5 Kebutuhan Gudang Kapasitas Pabrik 5 8 20 10 10 19 90 W = 0 H = 15 Gudang C = 14 50 40 110 40 Biaya transportasi = 90(5) + 50(15) + 10(20) + 10(10) + 40(19) = 2260 90 60 50 200

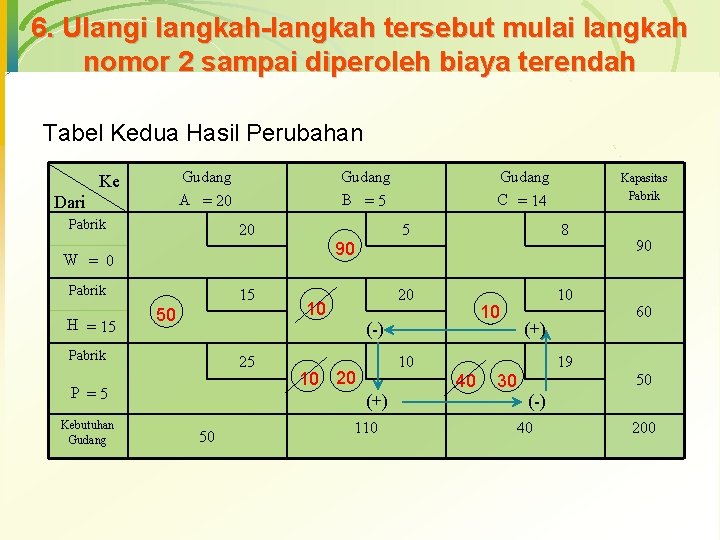
6. Ulangi langkah-langkah tersebut mulai langkah nomor 2 sampai diperoleh biaya terendah Tabel Kedua Hasil Perubahan Gudang A = 20 Ke Dari Pabrik Gudang B =5 20 90 W = 0 Pabrik H = 15 15 50 25 P =5 (+) 50 110 Pabrik 8 20 10 10 10 20 Kapasitas 5 10 (-) Pabrik Kebutuhan Gudang 10 Gudang C = 14 40 (+) 19 30 90 60 50 (-) 40 200

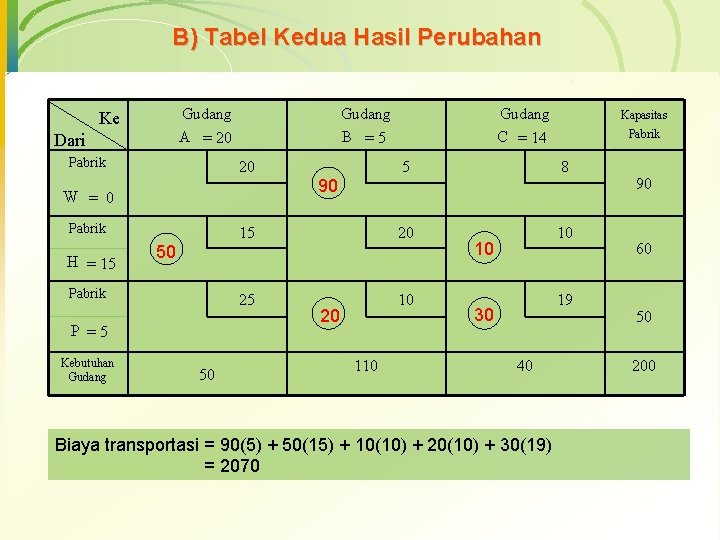
B) Tabel Kedua Hasil Perubahan Gudang A = 20 Ke Dari Pabrik Gudang B =5 20 H = 15 P =5 Kebutuhan Gudang 50 Pabrik 8 15 20 10 25 10 90 50 Pabrik Kapasitas 5 W = 0 Pabrik Gudang C = 14 20 110 10 19 30 40 Biaya transportasi = 90(5) + 50(15) + 10(10) + 20(10) + 30(19) = 2070 90 60 50 200

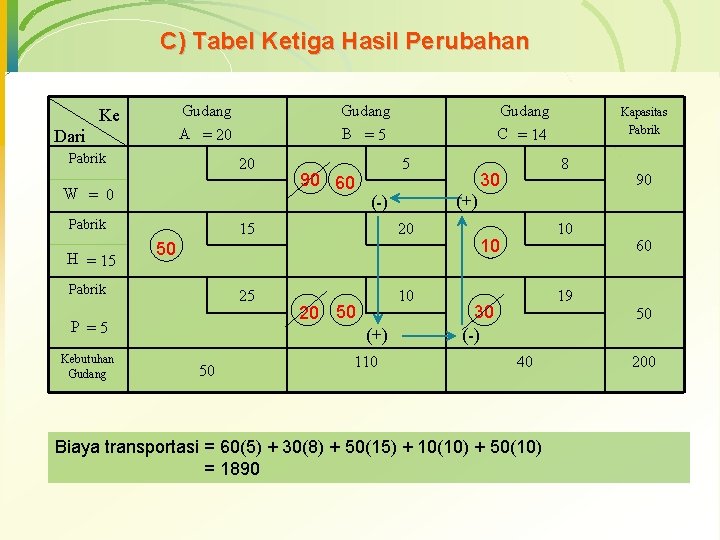
C) Tabel Ketiga Hasil Perubahan Gudang A = 20 Ke Dari Pabrik Gudang B =5 20 W = 0 Pabrik H = 15 5 15 20 25 10 P =5 20 50 (+) 50 110 Kapasitas Pabrik 8 30 90 (+) (-) 50 Pabrik Kebutuhan Gudang 90 60 Gudang C = 14 10 10 19 30 (-) 40 Biaya transportasi = 60(5) + 30(8) + 50(15) + 10(10) + 50(10) = 1890 60 50 200

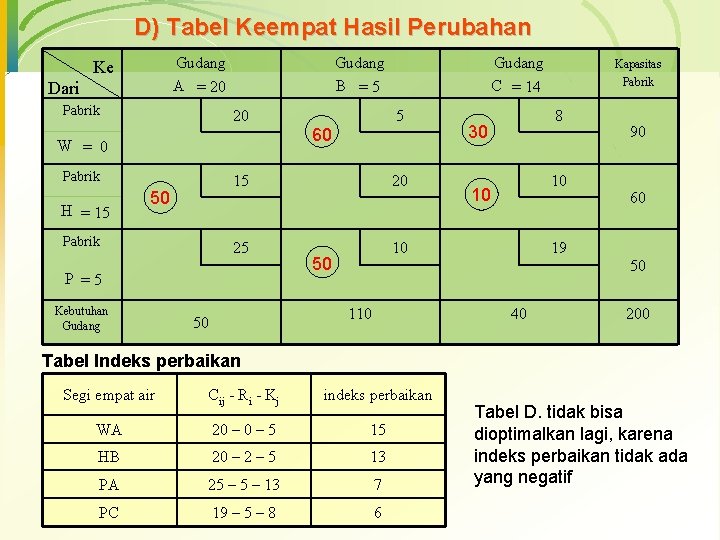
D) Tabel Keempat Hasil Perubahan Gudang A = 20 Ke Dari Pabrik Gudang B =5 20 5 60 W = 0 Pabrik H = 15 Gudang C = 14 50 Pabrik 15 20 25 10 P =5 Kebutuhan Gudang 50 110 50 Kapasitas Pabrik 8 30 10 10 19 40 90 60 50 200 Tabel Indeks perbaikan Segi empat air Cij - Ri - Kj indeks perbaikan WA 20 – 5 15 HB 20 – 2 – 5 13 PA 25 – 13 7 PC 19 – 5 – 8 6 Tabel D. tidak bisa dioptimalkan lagi, karena indeks perbaikan tidak ada yang negatif

Metode Vogel’s Approximation Langkah-langkah nya: 1. Susunlah kebutuhan, kapasitas masing-masing sumber, dan biaya pengangkutan ke dalam matrik 2. Carilah perbedaan dari dua biaya terkecil (dalam nilai absolut), yaitu biaya terkecil dan terkecil kedua untuk tiap baris dan kolom pada matrik (Cij) 3. Pilihlah 1 nilai perbedaan-perbedaan yang terbesar di antara semua nilai perbedaan pada kolom dan baris 4. Isilah pada salah satu segi empat yang termasuk dalam kolom atau baris terpilih, yaitu pada segi empat yang biayanya terendah di antara segi empat lain pada kolom/baris itu. Isiannya sebanyak mungkin yang bisa dilakukan

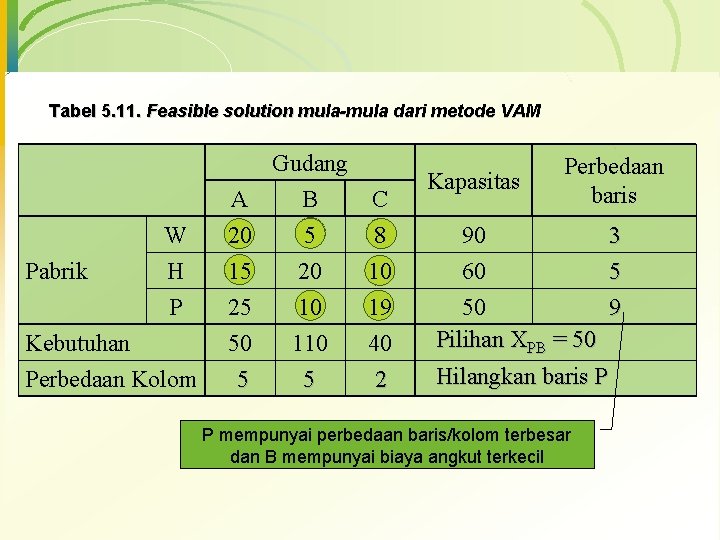
Tabel 5. 11. Feasible solution mula-mula dari metode VAM Pabrik Gudang A B C W 20 5 8 90 H 15 20 10 60 P 25 50 5 10 110 5 19 40 2 Kebutuhan Perbedaan Kolom Kapasitas Perbedaan baris 50 Pilihan XPB = 50 Hilangkan baris P P mempunyai perbedaan baris/kolom terbesar dan B mempunyai biaya angkut terkecil 3 5 9

Tabel 5. 11. Feasible solution mula-mula dari metode VAM Pabrik Gudang A B C W 20 5 8 90 H 15 20 10 60 50 5 60 15 40 2 Kebutuhan Perbedaan Kolom Kapasitas Perbedaan baris 3 5 Pilihan XWB = 60 Hilangkan kolom B Kebutuhan Gd B menjadi 60 krn telah diisi B mempunyai perbedaan baris/kolom kapasitas pabrik P=50 (dihilangkan) terbesar dan W mempunyai biaya angkut terkecil

Tabel 5. 11. Feasible solution mula-mula dari metode VAM Pabrik Gudang A B C W 20 8 30 H 15 10 60 50 5 40 2 Kebutuhan Perbedaan Kolom Kapasitas Pabrik W menjadi 30 krn telah W mempunyai perbedaan baris/kolom diangkut ke pabrik B=60 (dihilangkan) terbesar dan C mempunyai biaya angkut terkecil Kapasitas Perbedaan baris 12 5 Pilihan XWC = 30 Hilangkan baris W

Tabel 5. 11. Feasible solution mula-mula dari metode VAM Gudang A B C 15 10 50 10 Kapasitas Perbedaan baris 60 5 W Pabrik H Kebutuhan Perbedaan Kolom Pilihan XHA = 50 Pilihan XHC = 10 H mempunyai perbedaan baris/kolom Kebutuhan gudang C menjadi 10 krn terbesar dan C mempunyai biaya angkut telah diisi pabrik W=30 (dihilangkan) terkecil

Matrik hasil alokasi dengan metode VAM Ke Dari Gudang A Pabrik 20 W Pabrik H 50 Pabrik P Kebutuhan Gudang 50 Gudang B Gudang C 5 60 15 20 25 10 50 110 Kapasitas Pabrik 8 30 10 10 19 40 90 60 50 200 Setelah terisi semua, maka biaya transportasinya yang harus dibayar adalah 60(Rp 5, -) + 30(Rp 8, -) + 50(Rp 15, -) + 10(Rp 10, -) + 50(Rp 10, -) = Rp 1. 890, -

Metode VAM (Vogel Approkximation Method ) · Metode VAM lebih sederhana penggunaannya, karena tidak memerlukan closed path (jalur tertutup). Metode VAM dilakukan dengan cara mencari selisih biaya terkecil dengan biaya terkecil berikutnya untuk setiap kolom maupun baris. Kemudian pilih selisih biaya terbesar dan alokasikan produk sebanyak mungkin ke sel yang memiliki biaya terkecil. Cara ini dilakukan secara berulang hingga semua produk sudah dialokasikan.

Prosedur Pemecahan: (1) Hitung perbedaan antara dua biaya terkecil dari setiap baris dan kolom. (2) Pilih baris atau kolom dengan nilai selisih terbesar, lalu beri tanda kurung. Jika nilai pada baris atau kolom adalah sama, pilih yang dapat memindahkan barang paling banyak. (3) Dari baris/kolom yang dipilih pada (2), tentukan jumlah barang yang bisa terangkut dengan memperhatikan pembatasan yang berlaku bagi baris atau kolomnya serta sel dengan biaya terkecil. (4) Hapus baris atau kolom yang sudah memenuhi syarat sebelumnya (artinya suplai telah dapat terpenuhi). (5) Ulangi langkah (1) sampai (4) hingga semua alokasi terpenuhi.

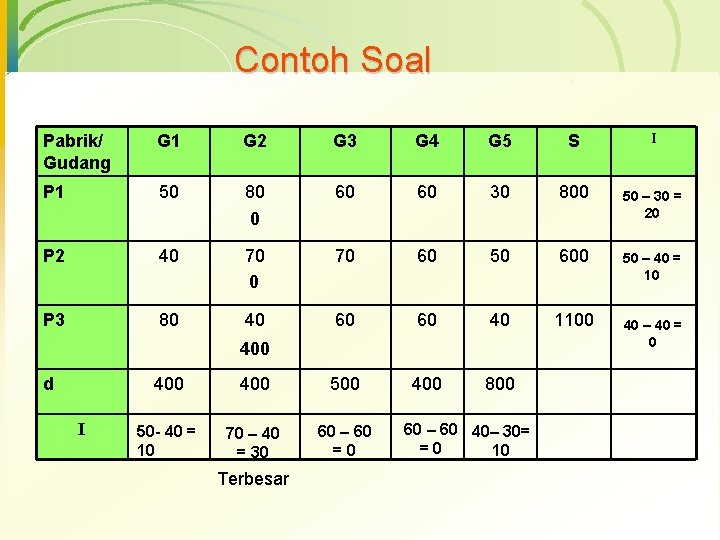
Contoh Soal Pabrik/ Gudang G 1 G 2 G 3 G 4 G 5 S P 1 50 80 60 60 30 800 0 P 2 40 70 60 50 600 P 3 80 40 60 40 1100 400 60 400 500 400 800 50 - 40 = 10 70 – 40 = 30 60 – 60 =0 d I Terbesar 60 – 60 40– 30= =0 10 I 50 – 30 = 20 50 – 40 = 10 40 – 40 = 0

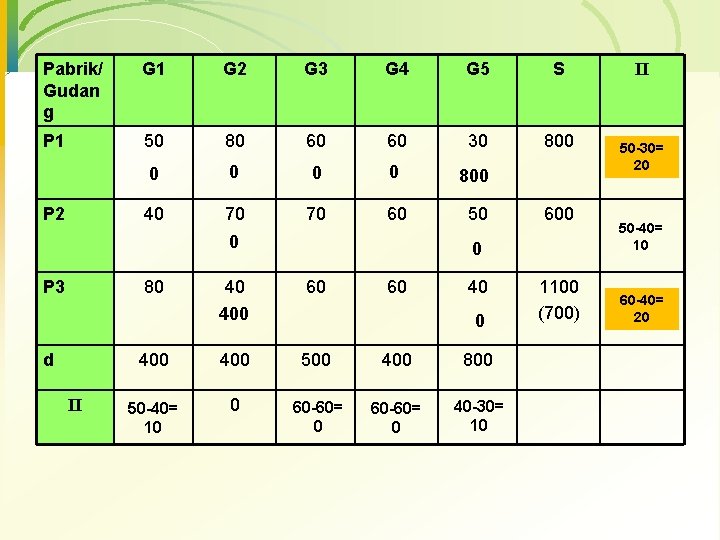
Pabrik/ Gudan g G 1 G 2 G 3 G 4 G 5 S P 1 50 80 60 60 30 800 0 0 800 40 70 70 60 50 P 2 0 P 3 80 d II 40 600 0 60 400 60 40 400 500 400 800 50 -40= 10 0 60 -60= 0 40 -30= 10 0 1100 (700) II 50 -30= 20 50 -40= 10 60 -40= 20

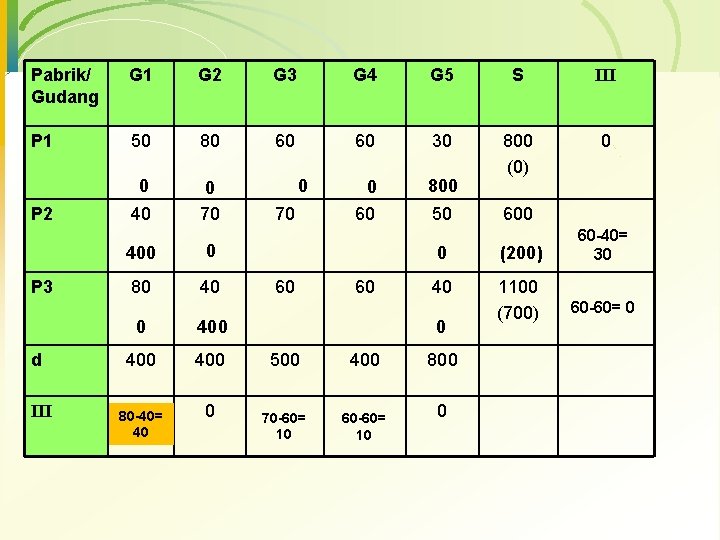
Pabrik/ Gudang G 1 G 2 G 3 G 4 G 5 S III P 1 50 80 60 60 30 0 70 0 60 800 (0) P 2 P 3 d III 40 400 0 80 400 400 80 -40= 40 0 0 70 60 500 400 70 -60= 10 60 -60= 10 50 600 0 (200) 60 -40= 30 40 1100 (700) 60 -60= 0 0 800 0

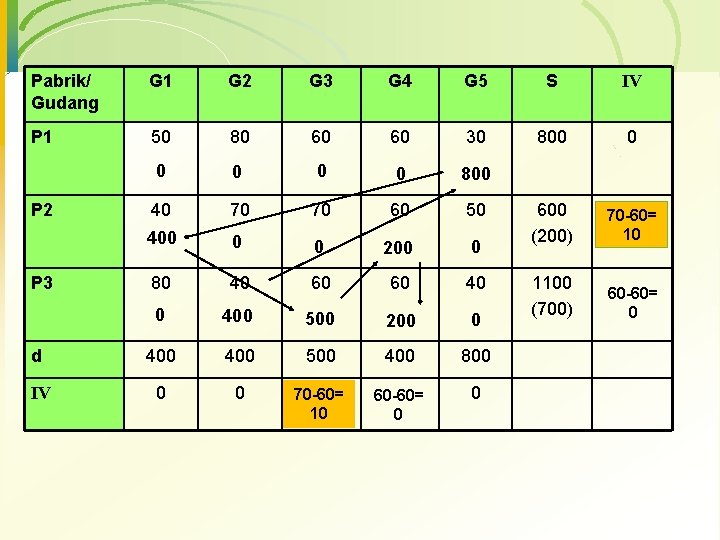
Pabrik/ Gudang G 1 G 2 G 3 G 4 G 5 S IV P 1 50 80 60 60 30 800 0 0 800 40 70 70 60 50 400 0 0 200 0 600 (200) 70 -60= 10 80 40 60 400 60 500 200 0 1100 (700) 60 -60= 0 d 400 500 400 800 IV 0 0 70 -60= 10 60 -60= 0 0 P 2 P 3

· Biaya Total = (400. 40) + (800. 30) + (400. 40) + (500. 60) + (200. 60) = 1. 100. 000

Tugas · Sebuah Perusahaan memproduksi Suatu Suku Cadang yang disetorkan kepada empat produsen mesin yaitu I, III dan IV. Suku cadang tersebut pada masing-masing cabang usaha perusahaan yang tersebar di tiga tempat yaitu A, B dan C. karena perbedaan efisiensi pada masing-masing tempat maka terjadi perbedaan biaya produksinya, yaitu biaya untuk memproduksi satu unit suku cadang di A adalah Rp 1, 10 dan di B dan C Rp 1, 03. Disamping itu, kapasitas produksi per bulan pada masing-masing tempat juga berbeda yaitu A = 7500 unit, B = 10000 unit dan C = 8100 unit. Permintaan suku cadang dari keempat produsen mesin itu adalah I = 4200 unit, II = 8300 unit, III = 6300 unit dan IV = 7200 unit.

Tugas (lanjut) · Biaya untuk mengirim satu unit suku cadang dari tiga cabang keempat produsen mesin itu Adalah : I II IV A 0. 12 0. 14 0. 08 0. 21 B 0. 13 0. 17 0. 10 0. 16 C 0. 15 0. 12 0. 14