MATERI 1 Program Linier Dengan Grafik RISET OPERASI

MATERI - 1 Program Linier Dengan Grafik

RISET OPERASI (1) • Merupakan ilmu interdisipliner yang menggunakan metode-metode ilmiah (pemodelan matematika, statistika) dan analisis kuantitatif untuk pengambilan keputusan. • Ketika diperhadapkan dengan pengambilan keputusan manajerial suatu proses bisnis, kata Riset operasi lebih disebut sebagai manajemen sains atau manajemen kuantitatif.

RISET OPERASI (2) Dalam riset operasi, faktor manusia sangat penting, karena riset operasi lebih dimaknai sebagai teknik untuk mengambil keputusan yang mampu memberikan berbagai solusi terhadap permasalahan sistem/proses bisnis yang ada.

PENERAPAN RISET OPERASI • Di bidang penerbangan (airlines) meminimalkan biaya, memaksimalkan keuntungan. • Di bidang telekomunikasi teori antrian, algoritma network. • Di bidang transportasi routing, logistik • Di bidang produksi inventori, simulasi, supply chain management. • Di bidang finance model kuantitatif

Pemrograman Linier (1) • Pemrograman linier (pemrograman di sini berarti memilih serangkaian tindakan/ perencanaan) merupakan suatu pendekatan pemecahan masalah yang dikembangkan untuk membantu para manajer mengambil keputusan. • Digunakan dengan tujuan memperoleh keuntungan yang maksimal dengan biaya yang minimal

Pemrograman Linier (2) • Program komputer yang dirancang untuk menyelesaikan masalah pemrograman linier antara lain LINDO, Qm dan Microsoft Excel-solver. • Maple

Pemrograman Linier (3) • Program linear dan variasinya merupakan kelompok teknik analisis kuantitatif yang mengandalkan model matematika (model simbolik). • Setiap penyelesaian masalah harus didahului dengan perumusan masalah ke dalam simbol-simbol matematika.

Pemrograman Linier (4) • Program linear pada hakekatnya merupakan salah satu teknik perencanaan yang bersifat analitis yang analisisnya memakai model matematika dengan tujuan menemukan beberapa kombinasi alternatif pemecahan masalah. • Pemrograman linear mencakup pemilihan serangkaian tindakan jika model matematis untuk suatu masalah hanya terdiri dari fungsi-fungsi linear (fungsi tujuan dan semua fungsi kendala linear).

Model PL (1) • Prosedur (umum) merumuskan model pemrograman linear 1. Menentukan jenis permasalahan program linear. • Jika permasalahan membicarakan keuntungan (profit), maka jenis permasalahan PL adalah maksimalisasi. • Jika permasalahan membicarakan biaya (cost), maka jenis permasalahan PL adalah minimalisasi. • Jika ada informasi tentang selisih antara hasil penjualan (sales) dan biaya dengan pokok pembicaraan profit, maka jenis permasalahannya adalah maksimalisasi.

Model PL (2) • Prosedur (umum) merumuskan model pemrograman linear 2. Mendefinisikan peubah keputusan (decision variable) • Umumnya peubah keputusan merupakan pernyataan dalam permasalahan yang hendak dicari penyelesaiannya. Beberapa hal yang harus diperhatikan adalah: – Banyaknya koefisien peubah keputusan seringkali dapat membantu dalam mengidentifikasikan peubah-peubah keputusan. – Jika x dimisalkan/diandaikan sebagai peubah keputusan berkaitan dengan kursi yang diproduksi, maka x kursi, tetapi x = banyaknya kursi yang diproduksi.

Model PL (3) • Prosedur (umum) merumuskan model pemrograman linear 3. Merumuskan kombinasi fungsi tujuan/sasaran (objective function) • • Kombinasi informasi tentang jenis permasalahan PL dan definisi peubah keputusan akan merumuskan fungsi tujuan. Jika peubah keputusan terdefinisi dengan jelas, maka fungsi tujuan akan mudah ditetapkan.

Model PL (4) • Prosedur (umum) merumuskan model pemrograman linear 4. Merumuskan model kendala/syarat ikatan (constraint) • Ada dua pendekatan umum untuk merumuskan model kendala: – Pendekatan Ruas Kanan » Maksimalisasi, kendala dengan tanda pertidaksamaan : » Minimalisasi, kendala dengan tanda pertidaksamaan : – Pendekatan Ruas Kiri » Semua koefisien dan peubah dinyatakan dalam bentuk matriks

Model PL (5) • Prosedur (umum) merumuskan model pemrograman linear 5. Menetapkan syarat non negatip • Setiap peubah keputusan dari kedua jenis permasalahan PL tidak boleh negatip (harus lebih besar atau sama dengan nol)

• • Pemrograman linear adalah rancangan model matematika untuk mengoptimumkan suatu fungsi tujuan yang memenuhi kendala yang ada. Pada program linear terdiri dari tiga elemen yaitu: – Variabel keputusan – Kendala – Fungsi objektif

Bentuk Umum PL (1)

Bentuk Umum PL (2)

Penyelesaian PL dengan Metode Grafik Masalah program linear dengan dua variabel dapat diselesaikan dengan metode grafik.

Penyelesaian PL dengan Metode Grafik Sebidang tanah seluas 30 m 2 akan ditanami 50 pohon jeruk dan apel, setiap satu pohon jeruk memakan tempat 1 m 2, sedang pohon apel ½ m 2. Setelah 5 tahun setiap pohon jeruk menghasilkan 20 ribu rupiah dan apel 15 ribu rupiah tiap pohonnya. Berapa pohon tiap jenis harus ditanam agar pada panen nanti didapatkan uang sebanyaknya (gunakan grafik untuk menyelesaikannya) !

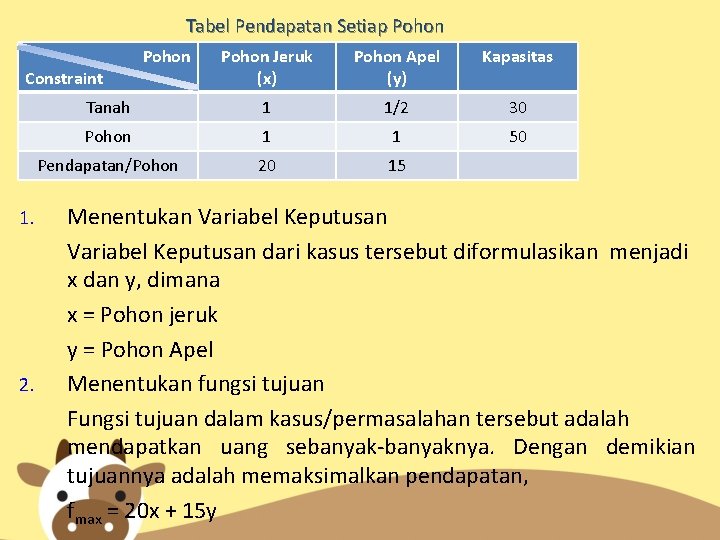
Penyelesaian : Berdasarkan data yang ada, maka permasalahan berapa pohon tiap jenis harus ditanam agar pada panen nanti didapatkan uang sebanyak-banyaknya, dapat disederhanakan dengan memasukkan angka-angka ke dalam tabel. Tabel Pendapatan Setiap Pohon Constraint Tanah Pohon Pendapatan/Pohon Jeruk Pohon Apel (x) (y) 1 1/2 1 1 20 15 Kapasitas 30 50

Tabel Pendapatan Setiap Pohon Jeruk (x) Pohon Apel (y) Kapasitas Tanah 1 1/2 30 Pohon 1 1 50 Pendapatan/Pohon 20 15 Constraint 1. 2. Pohon Menentukan Variabel Keputusan dari kasus tersebut diformulasikan menjadi x dan y, dimana x = Pohon jeruk y = Pohon Apel Menentukan fungsi tujuan Fungsi tujuan dalam kasus/permasalahan tersebut adalah mendapatkan uang sebanyak-banyaknya. Dengan demikian tujuannya adalah memaksimalkan pendapatan, fmax = 20 x + 15 y

Tabel Pendapatan Setiap Pohon Jeruk (x) Pohon Apel (y) Kapasitas Tanah 1 1/2 30 Pohon 1 1 50 Pendapatan/Pohon 20 15 Constraint 3. Pohon Menentukan Kendala (constraint) dari permasalahan linier tersebut Batasan untuk pendapatan setiap pohon adalah luas tanah yang ditanami, dan jumlah pohon yang ditanam. Kapasitas/persediaan masing-masing batasan adalah 30 m 2, dan 50 pohon Tanah : x + 1/2 y 30 Pohon : x + y 50

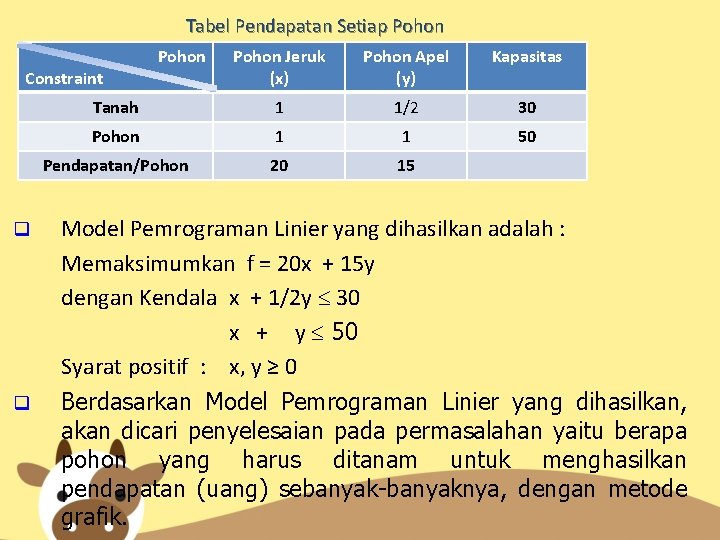
Tabel Pendapatan Setiap Pohon Jeruk (x) Pohon Apel (y) Kapasitas Tanah 1 1/2 30 Pohon 1 1 50 Pendapatan/Pohon 20 15 Constraint q q Pohon Model Pemrograman Linier yang dihasilkan adalah : Memaksimumkan f = 20 x + 15 y dengan Kendala x + 1/2 y 30 x + y 50 Syarat positif : x, y ≥ 0 Berdasarkan Model Pemrograman Linier yang dihasilkan, akan dicari penyelesaian pada permasalahan yaitu berapa pohon yang harus ditanam untuk menghasilkan pendapatan (uang) sebanyak-banyaknya, dengan metode grafik.

q Model Pemrograman Linier yang dihasilkan adalah : Memaksimumkan f = 20 x + 15 y dengan Kendala x + 1/2 y 30 x + y 50 Syarat positif : x, y ≥ 0 Penyelesaian : 1. Menentukan titik potong setiap kendala Kendala 1: x + 1/2 y 30 Perpotongan dengan sumbu x y = 0 x + 1/2. 0 = 30 x = 30 (30, 0) Perpotongan dengan sumbu y x = 0 0 + 1/2 y = 30 y = 60 (0, 60)

Kendala 2: x + y 50 Perpotongan dengan sumbu x y = 0 x + 0 = 50 x = 50 (50, 0) Perpotongan dengan sumbu y x = 0 0 + y = 50 (0, 50) Syarat positif : x, y 0

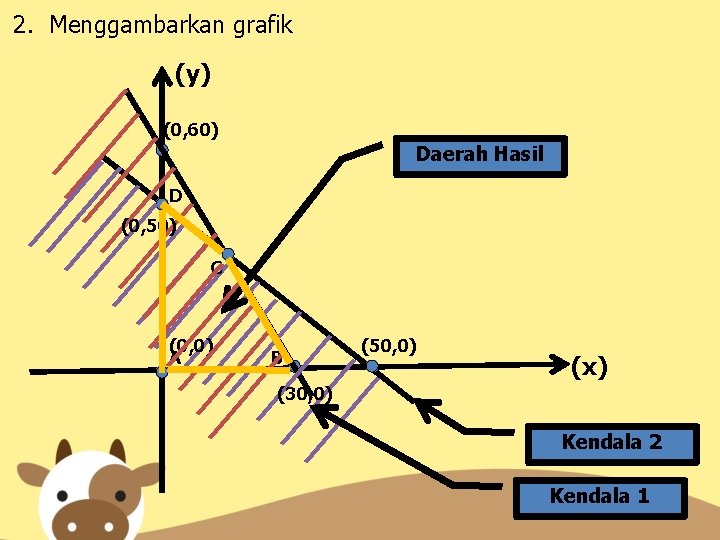
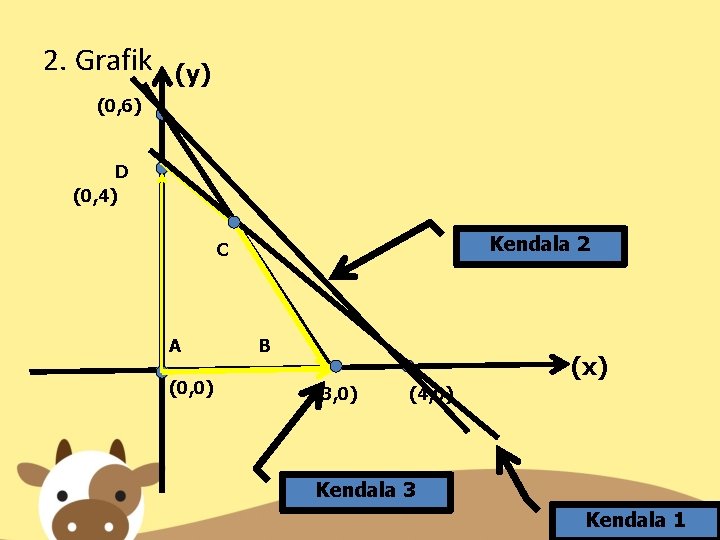
2. Menggambarkan grafik (y) (0, 60) Daerah Hasil D (0, 50) C (0, 0) A B (50, 0) (x) (30, 0) Kendala 2 Kendala 1

3. Menentukan titik-titik sudut Sudut A pada titik (0, 0) Sudut B pada titik (30, 0) Sudut C merupakan titik hasil perpotongan kendala 1 & 2: x + 1/2 y = 30 x + y = 50 -1/2 y = -20 y = 40 x + 40 = 50 (10, 40) x = 10 Sudut D pada titik (0, 50)

4. Membuat Tabel Optimal Sudut Titik fmax = 20 x + 15 y (0, 0) f = 20. 0 + 15. 0 = 0 A B (30, 0) f = 20. 30 + 15. 0 = 600 C (10, 40) f = 20. 10 + 15. 40 = 800 D (0, 50) f = 20. 0 + 15. 50 = 750 fmax = 800 5. Membuat Kesimpulan f = 20 x + 15 y mencapai nilai maksimum = 800, pada nilai x = 10 dan y = 40 Berdasarkan hasil tersebut, maka jumlah pohon yang harus ditanam untuk setiap jenis pohon adalah 10 pohon jeruk dan 40 pohon apel

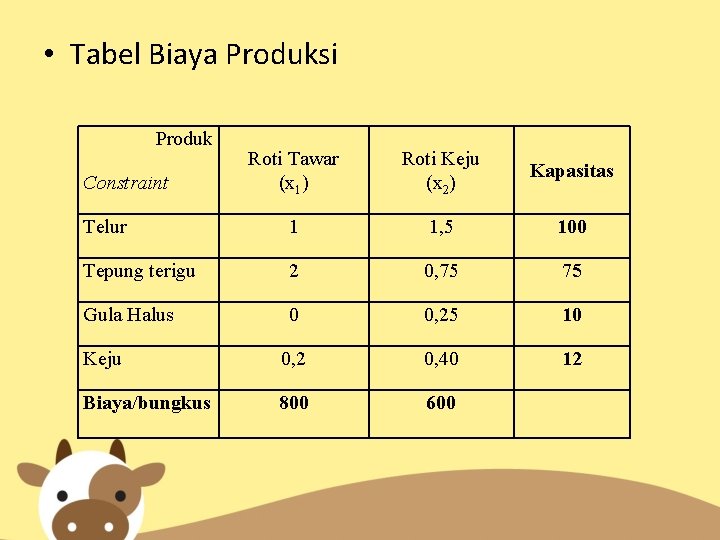
Penyelesaian PL dengan Metode Grafik • Perusahaan roti ”MAIP” telah menghitung biaya untuk memproduksi 2 jenis roti, yaitu roti tawar dan roti keju. Total biaya pembuatan roti tawar per bungkus sebesar Rp. 800, - dan roti keju sebesar Rp. 600, -. Untuk membuat roti keju dibutuhkan adonan yang terdiri atas: telur, tepung terigu, gula halus dan keju. Masing-masing sebanyak 1, 5 ons, 0, 75 ons, 0, 25 ons, 0, 4 blok. Untuk membuat roti tawar dibutuhkan adonan yang terdiri atas: telur, tepung terigu dan keju sebanyak 1 ons, 2 ons dan 0, 2 blok. Persediaan telur 100 ons, tepung terigu 75 ons, gula halus 10 ons dan keju 12 blok. Berapakah idealnya perusahaan memproduksi roti tawar dan roti keju dengan biaya yang dikeluarkan minimal? – – – Tentukan variabel keputusan kasus tersebut Tentukan fungsi tujuan kasus tersebut ! Tentukan kendala (constraint) kasus tersebut!

• Tabel Biaya Produksi Produk Roti Tawar (x 1) Roti Keju (x 2) Kapasitas Telur 1 1, 5 100 Tepung terigu 2 0, 75 75 Gula Halus 0 0, 25 10 Keju 0, 2 0, 40 12 Biaya/bungkus 800 600 Constraint

• Tentukan variabel keputusan kasus tersebut! Variabel keputusan roti ”MAIP” adalah 2 (dua). Variabel keputusan ini diformulasikan menjadi x 1 dan x 2, dimana : x 1 = Jumlah roti tawar x 2 = Jumlah roti keju

• Tentukan fungsi tujuan kasus tersebut ! Fungsi tujuan dalam permasalahan ini adalah pada biaya minimal. Dengan demikian, tujuan perusahaan roti ”MAIP” adalah minimalisasi biaya (Zmin) Zmin = 800 x 1 + 600 x 2

• Tentukan kendala (constraint) kasus tersebut! • Batasan untuk memproduksi roti tawar adalah telur, tepung terigu dan keju. Sedangkan batasan untuk memproduksi roti keju adalah telur, tepung terigu, gula halus dan keju. Persediaan masing batasan adalah 100 ons, 75 ons, 10 ons dan 12 blok. Telur : x 1 + 1, 5 x 2 100 Tepung terigu : 2 x 1 + 0, 75 x 2 75 Gula halus : 0, 25 x 2 10 Keju : 0, 2 x 1 + 0, 40 x 2 12 Syarat : x 1, x 2 0

Selesaikan masalah program linear berikut ini dengan metode grafik: • Maksimumkan f = 3 x 1 + 2 x 2 dengan kendala 2 x 1 + 2 x 2 8 3 x 1 + 2 x 2 12 x 1 + 0, 5 x 2 3 x 1, x 2 0

Penyelesaian : 1. Menentukan titik potong setiap kendala Kendala 1: 2 x 1 + 2 x 2 8 Perpotongan dengan x 1 x 2 = 0 2 x 1 + 0 = 8 2 x 1 = 8 x 1 = 4 (4, 0) Perpotongan dengan x 2 x 1 = 0 0 + 2 x 2 = 8 x 2 = 4 (0, 4)

Kendala 2: 3 x 1 + 2 x 2 12 Perpotongan dengan x 1 x 2 = 0 3 x 1 + 0 = 12 3 x 1 = 12 x 1 = 4 (4, 0) Perpotongan dengan x 2 x 1 = 0 0 + 2 x 2 = 12 x 2 = 6 (0, 6)

Kendala 3: x 1 + 0, 5 x 2 3 Perpotongan dengan x 1 x 2 = 0 x 1 + 0 = 3 x 1 = 3 (3, 0) Perpotongan dengan x 2 x 1 = 0 0 + 0, 5 x 2 = 3 x 2 = 6 (0, 6) • Syarat positif : x 1, x 2 0

2. Grafik (y) (0, 6) D (0, 4) Kendala 2 C A (0, 0) B (x) (3, 0) (4, 0) Kendala 3 Kendala 1

3. Menentukan titik-titik sudut Sudut A pada titik (0, 0) Sudut B pada titik (3, 0) Sudut C merupakan titik hasil perpotongan kendala 1 & 3 : 2 x 1 + 2 x 2 = 8 x 1 + 0, 5 x 2 = 3 2 x 1 + 2 x 2 = 8 2 x 1 + x 2 = 6 ---------- _ x 2 = 2 2 x 1 + 2. 2 = 8 2 x 1 + 4 = 8 2 x 1 = 4 x 1 = 2 (2, 2) Sudut D pada titik (0, 4)

Kejadian khusus pada masalah program linear dengan dua variabel • • • Masalah program linear belum tentu mempunyai satu penyelesaian optimal. Ada tiga kejadian khusus dari masalah program linear yaitu: Masalah program linear mempunyai beberapa penyelesaian. Contoh : Maksimumkan Z = 300 x 1 + 200 x 2 Dengan kendala : 6 x 1 + 4 x 2 240 x 1 + x 2 50 x 1 , x 2 0

Kejadian khusus pada masalah program linear dengan dua variabel • • Masalah program linear tidak mempunyai penyelesaian optimal (infeasible solution). Contoh : Maksimumkan Z = x 1 + x 2 Dengan kendala : x 1 + x 2 4 x 1 - x 2 5 x 1 , x 2 0

Kejadian khusus pada masalah program linear dengan dua variabel • • Masalah program linear mempunyai penyelesaian tak terbatas (unbounded solutions) masalah program linear tidak mempunyai penyelesaian optimal. Contoh : Maksimumkan Z = 2 x 1 - x 2 Dengan kendala : x 1 - x 2 1 2 x 1 + x 2 6 x 1 , x 2 0