Problem Complexity Review Problem Complexity LB Online Survey

Problem Complexity Review

Problem Complexity

LB Online Survey The Spring term course/instructor opinion survey will be available during the period Monday, April 17 th through Friday, April 28 th from 6 am to 11: 59 pm each day: http: //www. coursesurvey. gatech. edu

LB Final Exam Schedule • CS 1311 Sections L/M/N Tuesday/Thursday 10: 00 A. M. • Exam Scheduled for 8: 00 Friday May 5, 2000 • Physics L 1

LB Final Exam Schedule • CS 1311 Sections E/F Tuesday/Thursday 2: 00 P. M. • Exam Scheduled for 2: 50 Wednesday May 3, 2000 • Physics L 1
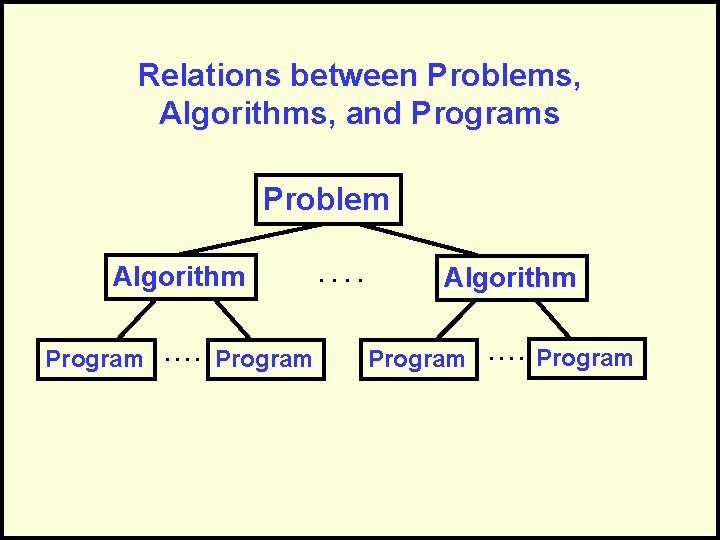
Relations between Problems, Algorithms, and Programs Problem Algorithm Program . . . . Algorithm Program . . Program

Cost and Complexity • Algorithm complexity can be expressed in Order notation, e. g. “at what rate does work grow with N? ”: – O(1) Constant – O(log. N) Sub-linear – O(N) Linear – O(Nlog. N) Nearly linear – O(N 2) Quadratic – O(XN) Exponential • But, for a given problem, how do we know if a better algorithm is possible?

The Problem of Sorting For example, in discussing the problem of sorting: • Two algorithms to solve: – Bubblesort – O(N 2) – Mergesort – O(N Log N) • Can we do better than O(N Log N)?

Algorithm vs. Problem Complexity • Algorithmic complexity is defined by analysis of an algorithm • Problem complexity is defined by – An upper bound – defined by an algorithm – A lower bound – defined by a proof

The Upper Bound • Defined by an algorithm • Defines that we know we can do at least this good • Perhaps we can do better • Lowered by a better algorithm – “For problem X, the best algorithm was O(N 3), but my new algorithm is O(N 2). ”

The Lower Bound • Defined by a proof • Defines that we know we can do no better than this • It may be worse • Raised by a better proof – “For problem X, the strongest proof showed that it required O(N), but my new, stronger proof shows that it requires at least O(N 2). ”

Upper and Lower Bounds • The Upper bound is the best algorithmic solution that has been found for a problem. – “What’s the best that we know we can do? ” • The Lower bound is the best solution that is theoretically possible. – “What cost can we prove is necessary? ”
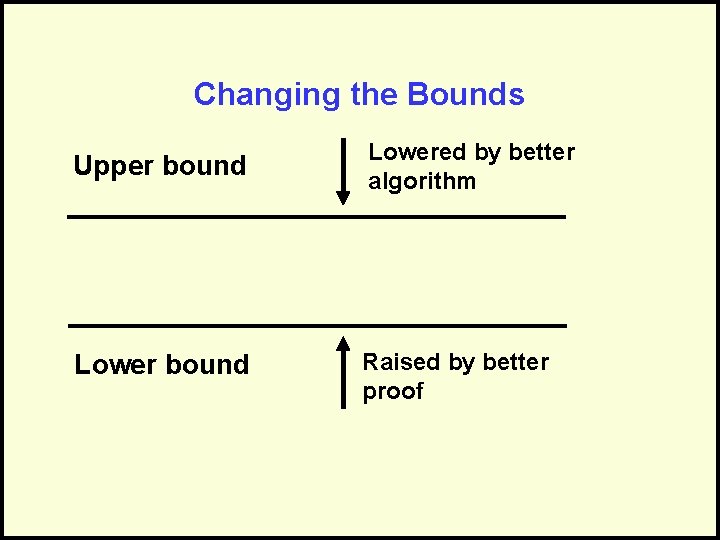
Changing the Bounds Upper bound Lowered by better algorithm Lower bound Raised by better proof
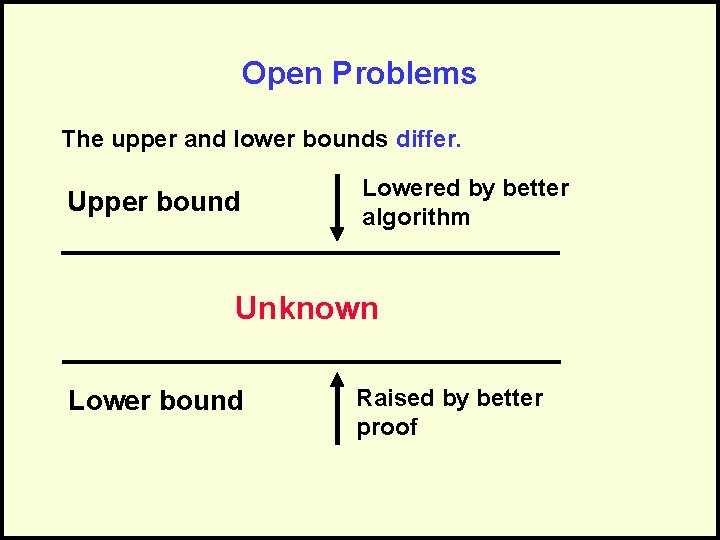
Open Problems The upper and lower bounds differ. Upper bound Lowered by better algorithm Unknown Lower bound Raised by better proof

Closed Problems The upper and lower bounds are identical. Upper bound Lower bound

Closed Problems • Better algorithms are still possible • Better algorithms will not provide an improvement detectable by “Big O” • Better algorithms can improve the constant costs hidden in “Big O” characterizations

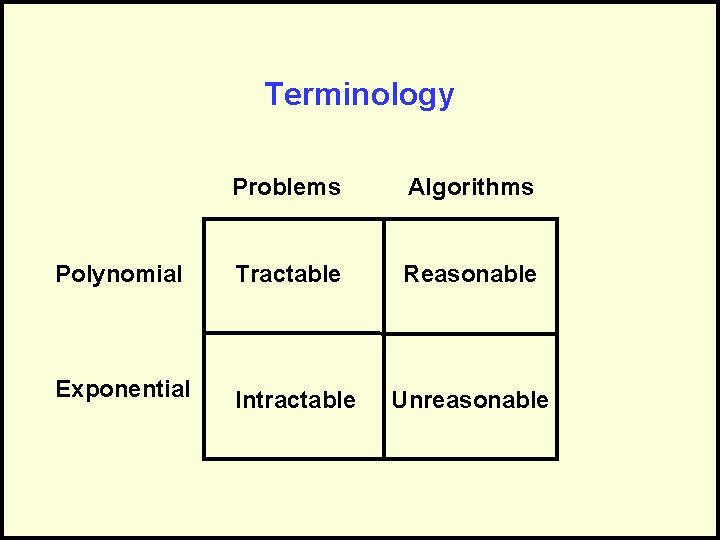
Tractable vs. Intractable Problems are tractable if the upper and lower bounds have only polynomial factors. – O (log N) – O (NK) where K is a constant Problems are intractable if the upper and lower bounds have an exponential factor. – O (N!) – O (NN) – O (2 N)

Problems that “Cross the Line” • The upper bound implies intractable • The lower bound implies a tractable • Could go either way… Next time!!!

Terminology • Polynomial algorithms are reasonable • Polynomial problems are tractable • Exponential algorithms are unreasonable • Exponential problems are intractable
Terminology Problems Algorithms Polynomial Tractable Reasonable Exponential Intractable Unreasonable

Questions?

Review • The Algorithmic Model – Algorithm defined – Properties of good algorithms – How to describe algorithms – Relating problems to algorithms to programs (hierarchy needed)

Review • View of programming languages/algorithms – Data vs. instructions – Built-in vs. user-defined – Complex vs. atomic • Data – Type vs. variable (Declaration and Initialization of variables) – The 4 atomic built-in types (Num, Characters, Booleans, Pointers) – The complex built in type String

Review • Operations – Assignment – Arithmetic • +, -, x, /, div, mod • Precedence rules • Using parenthesis to modify precedence – Input and output • Print • Read

Review • Conditionals – Purpose & defined – Relational operators (<, >, =, <>, >=, <=) – Boolean operators (AND, OR, NOT) – Boolean expressions (Simple & Complex) – Control flow of the if-then-else statement – Elseif as shorthand • Writing an algorithm (how to begin)

Review • Program maintenance • Software Engineering facts about program cost • Documentation • Benefits of Constants

Review • Procedural Abstraction • Why modularity (Benefits) • Need for interface • Scope of variables • Contract (Pre, post, and purpose statements for every module) • Information flow – in, out, in/out • Parameters intro (In, out, in/out) • Types of modules

Review • Procedure • Rules when to use a procedure • Declaration • Function • Rules when to use a function • Declaration • Returning values via the “returns”

Review • Module invocation • Parameters • Formal vs. actual • Parameter matching • How parameters work (In, Out, & In/out) • Tracing • Activation stack • Frames • Rules of parameter matching (In, Out, & In/out) • Examples

Review • Recursion (Intro) • Purpose – repetition • Characteristics – calls itself, terminating condition, move closer • 2 forms – final action or not • Examples • Tracing recursive modules • Recursion (Advanced) • Mutual recursion • Design by Contract

Review • Data Abstraction – Records • Declaring records • Creating variables of record type • Accessing fields of a record variable (the ‘. ’ operator) • Avoid anonymous types • Combining records (records inside records)

Review • Static vs. dynamic memory/data • Pointers • Simple example of ptr toa num • Following the pointer via the ‘^’ operator • Dynamic data structures • Linked Lists • Defined/properties • Proper Record declaration • Accessing information in a linked list via pointers

Review • Linked Lists (continued) – Adding nodes – Simple – no recursion (To front) – Insertion recursive method – To end – In middle (when sorted) – Deleting nodes • Simple - no recursion (From front) • Deletion recursive method

Review • Doubly-linked lists – Defined – Example methods (simple insertion) • Stack – Defined/properties – Push – Pop – Tracing changes (example of algorithm using push & pop)

Review • Queue • Defined/properties • Enqueue • Dequeue • Tracing changes (example of algorithm using enqueue and dequeue) • Trees • Defined/properties • Binary trees (Record declaration) • Binary search trees

Review • Trees (Continued) • Recursive insertion in BST • Deleting from BST (conceptually) • Graphs • Defined/properties • Record definition

Review • Static data structures • Arrays • Defined • Need of constants • Accessing elements via the index • Multi-dimensional arrays (Declaring and accessing)

Review • Iteration • Defined, use for repetition • How looping works • Loop • Endloop • Exitif • Combined types • Examples – array of lists, list of array, tree of lists, etc.

Review • Methods of Accessing Data Structures • Traversal • Lists • Recursive on lists • Iterative on lists • Trees • In-order • Pre-order • Post-order • Miscellaneous Traversals • (Rt before Left)

Review • Breadth-first vs. depth- first • Arrays • Iterative on arrays • Recursive on arrays • Search • Linear • Recursive on lists • Traversal-search on binary tree (not BST) • Linear, iterative search on array

Review • Binary, recursive search on BST • Binary, iterative search on sorted array • Sort • Bubble sort • Merge sort

Review • Conversion • Defined • Helper module advantages • List to Tree • Array to List • Tree to List

Review • Optimization • Defined & example problems • Greedy algorithms • Dynamic programming • Minimum spanning trees • Defined • Prim’s algorithm • Kruskal’s algorithm

Review • Object-Oriented • Defined • Behavioral abstraction (Defined & Advantages) • Encapsulation • Abstract data types • Queue & stack examples • Need formal programmatic construct

Review • Classes • Defined • Advantages • Structure - public & protected • Role for each • Benefits • Examples • Scope of attributes in protected

Review • Initialize (not built-in, but useful) • Using classes • Declaring objects • Objects vs. classes • Accessing methods via the ‘. ’ Operator • Example Classes • Airplane example • Queue example • Pile example

Review • Generic classes • Defined & benefits • Search and replace type then use a “magic” keyword • Syntax • Defining objects in algorithm • Use cases • Clone vs. copy • Inheritance • Defined & benefits • Extension • Redefinition

Review • Resolving method reference ambiguity • Class hierarchies • Deferred class & methods • Polymorphism • Defined & benefits • Simple assignment example • Complex collection example • Pure OO

Review • Algorithm Cost and Complexity • Measuring performance (space & time) • Measuring work (counting instructions) • Best, worst, average • Measuring work growth • O() notation • Complex O() rules (drop constants, keep dominant term, etc. )

Review • Analysis – Linear vs. binary search – Traversals – Data structures • Compare on traversals, search, & insert – Bubblesort vs. mergesort • Exponential growth – Hanoi, Monkey tiling, wise peasant • Reasonable vs. unreasonable • Using O() analysis in data structure design of solution

Review • Systems – Concurrency vs. sequential processing (what we’ve done so far) • Defined & advantages • Multiprogramming • Multiprocessing • Multitasking • Distributed systems

Review • Issues – Protection, mutual exclusion – Starvation, fairness – Deadlock – Time – Synchronization – Overhead costs (context switch)

Review • Parallelism – Defined & advantages – Pipeline processing – Product complexity • Dependencies • Precedence – Dependence Graphs – Precedence Graphs

Review • Problem Complexity – Defined – Problems vs. algorithms – Upper bound – Lower bound – Open vs. closed – Tractable vs. intractable

Review • NP-Complete – Defined – Examples – Certificates – Oracles – Deterministic vs. nondeterministic • Decidable vs. undecidable • Highly vs. partially

Questions? Review slides available at http: //prism. gatech. edu/~wl 48 Double U Ell

- Slides: 57