Tigbur 3 1 Complexity MergeSort Complexity Recurrence Relation

Tigbur 3. 1 Complexity Merge-Sort

Complexity

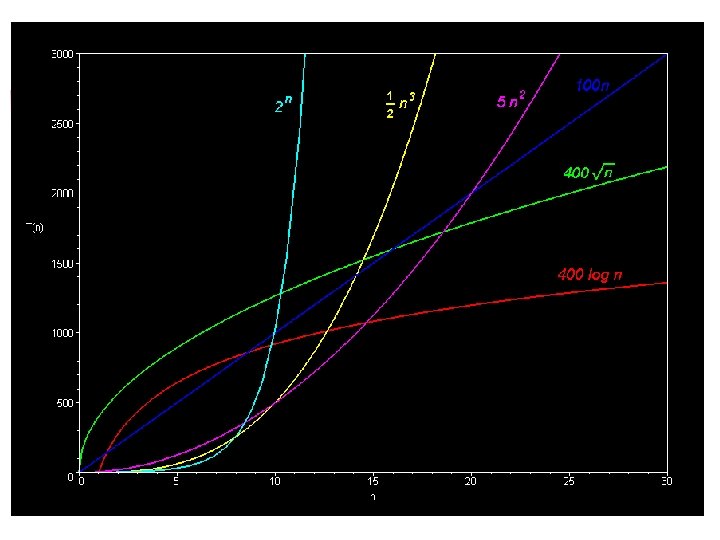
Recurrence Relation: Insertion Sort, Selection Sort, Bubble Sort n n T(n) = T(n - 1) + O(n) T(1) = O(1) [constant time] Array of size 1 – solved in constant time (base case) These relationships are called a recurrence relation because the function T( ) occurs on both sides of the = sign; it should remind you of recursive specifications This recurrence relation describes the sorting functions: insertion, selection, bubble If we could solve the recurrence relation we would know the complexity of these sort algorithms since T(n) is the time for them to execute

Recurrence Relations to Know and Love n T(n) = T(n – 1) + O(n) Selection / Insertion / Bubble Sort O(n 2) n T(n) = T(n – 1) + O(1) Sequential Search O(n) n T(n) = T(n/2) + O(1) Binary Search O(log 2 n)

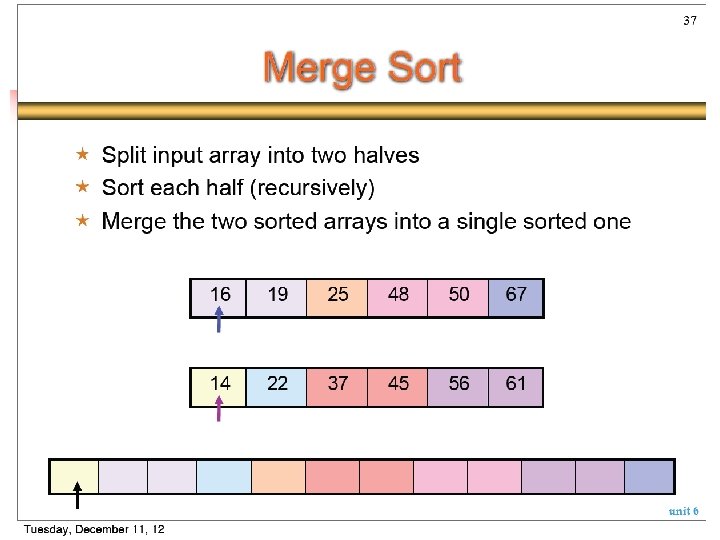
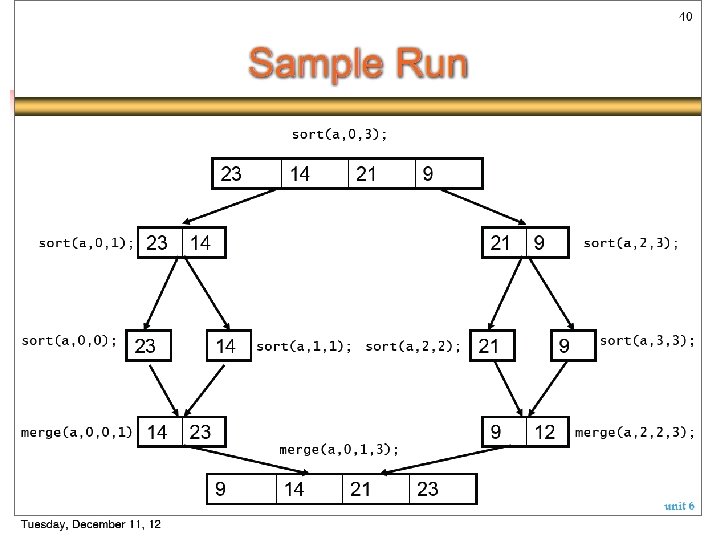
Merge-Sort

Find Sum x+y=z static boolean Find. Sum(int []data, int z){ for (int i=0; i < data. length; i++){ for (int j=i+1; j<data. length; j++){ if (data[i]+data[j] == z){ System. out. println("x=" + data[i] + " and y=" + data[j]); return true; } } } return false; } How do we show the complexity? 21

Complexity n Remember the analysis for Bubble Sort: n n First loop has n iterates. Inner loop:

Find Sum in sorted array x+y=z static boolean Find. Sum. Sorted(int []data, int z){ int lower=0, upper=data. length-1; while ((data[lower]+data[upper] != z) && (lower < upper)) { if (data[lower]+data[upper] > z) upper--; else if (data[lower]+data[upper] < z) lower++; } if (lower >= upper) { return false; } else { System. out. println("x=" + data[lower] + " and y=" + data[upper]); } return true; Complexity? } 23