Tirgul 10 Complexity Sorting Searching Complexity A motivation








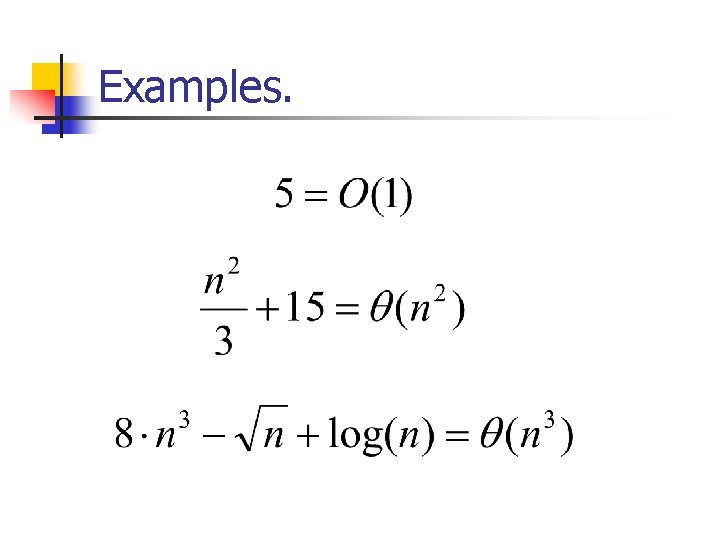






![Bubble Sort public static void bubble 1(int[] data) { for(int j=0; j<data. length-1; j++){ Bubble Sort public static void bubble 1(int[] data) { for(int j=0; j<data. length-1; j++){](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-17.jpg)



![Bubble Sort public static void bubble 1(int[] data) { for(int j=0; j<data. length-1; j++){ Bubble Sort public static void bubble 1(int[] data) { for(int j=0; j<data. length-1; j++){](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-21.jpg)
![Modified Bubble Sort public static void bubble 2(int[] data) { for(int j=0; j<data. length-1; Modified Bubble Sort public static void bubble 2(int[] data) { for(int j=0; j<data. length-1;](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-22.jpg)




![Insert Sort public static void insert. Sort(int[] data){ for(int i=1; i<data. length; i++){ //assume Insert Sort public static void insert. Sort(int[] data){ for(int i=1; i<data. length; i++){ //assume](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-27.jpg)


![Bucket Sort public static void bucket. Sort(int[] data, int max. Val){ int[] temp; temp=new Bucket Sort public static void bucket. Sort(int[] data, int max. Val){ int[] temp; temp=new](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-30.jpg)



![Finding the smallest difference The naïve way: public static int minimal. Dif(int[] numbers){ int Finding the smallest difference The naïve way: public static int minimal. Dif(int[] numbers){ int](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-34.jpg)



![Linear search in a sorted array public static int linear. Search(int[] int. Arr, int Linear search in a sorted array public static int linear. Search(int[] int. Arr, int](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-38.jpg)



![The Binary Search Java Code int binary. Search (int[ ] data, int num) { The Binary Search Java Code int binary. Search (int[ ] data, int num) {](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-43.jpg)















![Solution Tip: Explain and document your code public static int common 1(int[] arr){ int Solution Tip: Explain and document your code public static int common 1(int[] arr){ int](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-60.jpg)
![Counts the number of times arr[index] appears from index and onwards. Tip: Break code Counts the number of times arr[index] appears from index and onwards. Tip: Break code](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-61.jpg)
![A small optimization public static int common 1(int[] arr){ int most. Common = 0; A small optimization public static int common 1(int[] arr){ int most. Common = 0;](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-62.jpg)






![Common 3 private static int ALLOWED_VALS = 100; public static int common 3(int[] arr){ Common 3 private static int ALLOWED_VALS = 100; public static int common 3(int[] arr){](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-70.jpg)


![Ternary Search static int Ternary(int []data, int key) { int pivot 1, pivot 2, Ternary Search static int Ternary(int []data, int key) { int pivot 1, pivot 2,](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-73.jpg)

![Find Sum x+y=z static boolean Find. Sum(int []data, int z){ for (int i=0; i Find Sum x+y=z static boolean Find. Sum(int []data, int z){ for (int i=0; i](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-75.jpg)

![Find Sum in sorted array x+y=z static boolean Find. Sum. Sorted(int []data, int z){ Find Sum in sorted array x+y=z static boolean Find. Sum. Sorted(int []data, int z){](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-77.jpg)
- Slides: 77

Tirgul 10 Complexity Sorting Searching

Complexity

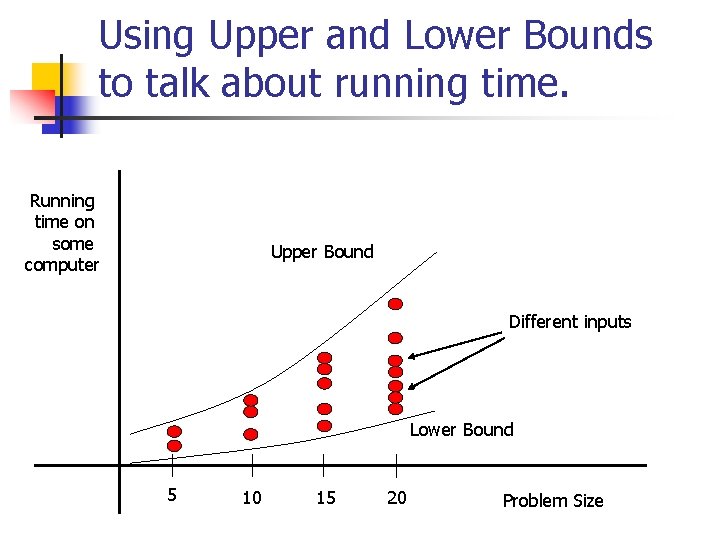
A motivation for complexity n Talking about running time of algorithms is difficult. n n n Different computers will run them at different speeds Different problem sizes run for a different amount of time (even on same computer). Different inputs of the same size run for a different amount of time.

Using Upper and Lower Bounds to talk about running time. Running time on some computer Upper Bound Different inputs Lower Bound 5 10 15 20 Problem Size

Bounds on running time n We want to bound the running time: n n n “for arrays of size n it takes my computer 45·n 2 milliseconds at most to sort the array with bubblesort” But what about other computers? (faster/slower) Instead we say: n n “On any computer, there is a constant c such that it takes at most c·n 2 time units to sort an array of size n with bubblesort” How is this sentence useful?

Big O notation. We say that running time of an alg. is O(f(n)) If there exists c such that for large enough n: Running. Time(n) < c·f(n) n Translation: From some point c·f(n) is an upper bound on the running time. n Why only for “large enough n”?

Use of big-O notation Example: The running time of bubble sort on arrays of size n is O(n 2). Translation: for a sufficiently large array, the running time is less than c·n 2 for some c (No matter how bad the input is). n

Big Omega n n For lower bounds we use Ω(f(n)). I. e. , if we say the running time of an algorithm is Ω(f(n)), we mean that Running. Time(n)>c·f(n) for some c.

Big-O notation n n Do not assume that because we analyze running time asymptotically we no longer care about the constants. If you have two algorithms with different asymptotic limits – easy to choose. n n (may be misleading if constants are really large). Usually we are happy when something runs in polynomial time and not exponential time. O(n 2) is much better than O(2 n).
Examples.

Examples n What is the running time of the following code: for (int i = 0; i < arr. length; i++) { System. out. println(arr[i]); }

Examples n What about this code: for (int i = 0; i < arr. length; i++) { if (arr[i]==1) break; System. out. println(arr[i]); }

Examples n Checking if the number n is prime. n n We can try and divide the number n by all integers in the range 2, …, n 1/2. Best case: sometimes we find it isn’t prime really quickly (e. g. it divides by 2). Worst case: sometimes the number is prime and we try n 1/2 different divisions. Running time is O(n 1/2), and is also Ω(1).

Bounds might not be tight n n n We saw that finding out if a number n is prime takes us O(n 1/2) time. It also takes us O(n 5) time. The second bound guarantees less. It is not tight.

Space Complexity n n n The amount of memory a certain algorithm requires matters to us. Do we have enough memory to run it? When we say something like ‘the space complexity of this algorithm is O(n 2)’ we mean: there exists a ‘c’ such that there at most c*n 2 memory cells used by the alg. at any given time.

Sorting
![Bubble Sort public static void bubble 1int data forint j0 jdata length1 j Bubble Sort public static void bubble 1(int[] data) { for(int j=0; j<data. length-1; j++){](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-17.jpg)
Bubble Sort public static void bubble 1(int[] data) { for(int j=0; j<data. length-1; j++){ for (int i=1; i<data. length-j; i++){ if(data[i-1]>data[i]){ swap(data, i-1, i); } } The internal loop runs n-1 times, then n-2 times, then n-3 times and so on… What is the complexity?

Bubble Sort

Analysis of Running Time n Let’s assume the swapping procedure along with the if that surrounds it run in at most k time units. Total running time is then at most: n What is the lower bound? n

A Stable Sorting Algorithm n n A sorting algorithm is called ‘stable’ if it maintains the original order of two equal items. Example: Original Array Result of a stable sort A non-stable sort 4 3 2 a 1 a 1 b 2 b 1 a 1 b 2 a 2 b 3 4 1 a 1 b 2 b 2 a 3 4
![Bubble Sort public static void bubble 1int data forint j0 jdata length1 j Bubble Sort public static void bubble 1(int[] data) { for(int j=0; j<data. length-1; j++){](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-21.jpg)
Bubble Sort public static void bubble 1(int[] data) { for(int j=0; j<data. length-1; j++){ for (int i=1; i<data. length-j; i++){ if(data[i-1]>data[i]){ swap(data, i-1, i); } } Question: Is this a stable sort? Question: What happens if we start this on a sorted array?
![Modified Bubble Sort public static void bubble 2int data forint j0 jdata length1 Modified Bubble Sort public static void bubble 2(int[] data) { for(int j=0; j<data. length-1;](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-22.jpg)
Modified Bubble Sort public static void bubble 2(int[] data) { for(int j=0; j<data. length-1; j++){ boolean moved. Something = false; //added this for (int i=1; i<data. length-j; i++){ if(data[i-1]>data[i]){ moved. Something = true; //added this swap(data, i-1, i); } } if(!moved. Something) break; //added this } } We detect when the array is sorted and stop in the middle.

Modified Bubble Sort Before the modification, running time was always nearly the same but now what? n What is the best case? What is the worst case? What is the running time in each case? n Which version of bubble sort is better? n n

Complexity of Modified Bubble Sort. n n What is the worst case running time? O(n 2) - The array is sorted in reverse – we don’t exit early. What is the best case running time? Ω(n) – in the best case we start with a sorted array. Go over it once and see that nothing was moved.

Selection Sort (a. k. a. Max-Sort) Pseudo Code: n For i=0, 1, …, n-2 n Run over the array from i onwards. n n Find j- the index of the minimal item. Swap the values in indexes i, j.

Running Time of selection sort n n Note first that the running time is always pretty much the same. Finding the minimal value always requires us to go over the entire sub-array. There is no shortcut, and we never stop early. First, we have an array of size n-1 to scan, then size n-2… We’ve already analyzed this pattern: Running time is O(n 2).
![Insert Sort public static void insert Sortint data forint i1 idata length i assume Insert Sort public static void insert. Sort(int[] data){ for(int i=1; i<data. length; i++){ //assume](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-27.jpg)
Insert Sort public static void insert. Sort(int[] data){ for(int i=1; i<data. length; i++){ //assume before index i the array is sorted insert(data, i); //insert i into array 0. . . (i-1) } } private static void insert(int[] data, int index) { int value = data[index]; int j; for(j=index-1; j>=0 && data[j]>value; j-- ){ data[j+1]=data[j]; } data[j+1] = value; }

Complexity of Insertion Sort n Worst case complexity: n n O(n 2) – If the original array is sorted backwards we insert all the way in. First into an array of size 1, then 2, then 3… Is this pattern familiar? Best case complexity: n Ω(n) – The array is already sorted. Each insert stops after 1 step, but we call insert Ω(n) times.

Bucket Sort n Elements are distributed among beans: n Elements are sorted within each bin:
![Bucket Sort public static void bucket Sortint data int max Val int temp tempnew Bucket Sort public static void bucket. Sort(int[] data, int max. Val){ int[] temp; temp=new](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-30.jpg)
Bucket Sort public static void bucket. Sort(int[] data, int max. Val){ int[] temp; temp=new int[max. Val+1]; int k=0; for(int i=0; i<data. length; i++) temp[data[i]]++; for (int i=0; i<=max. Val ; i++) for (int j=0; j<temp[i]; j++){ data[k]=i; k++; } }

Complexity of Bucket Sort n Worst case complexity: n n Best case complexity: n n O(n 2) Ω(n) Average case complexity: n Ω(n) – if the distribution of elements in the array is uniform.

Conclusions: n The Lesson: n n n Pick the right algorithm for the job. If we know the array is nearly sorted some algorithms may be better. Soon to come: n n Sorting algorithms that sort in O(n·log(n)) This is the best you can do without assumptions on the data (There is a formal proof but we will not learn it in this course).

Why Sort? n n n Faster search (Binary Search). Other things may also work faster. Another Example: Given an array of numbers, find the pair with the smallest difference. Return the difference.
![Finding the smallest difference The naïve way public static int minimal Difint numbers int Finding the smallest difference The naïve way: public static int minimal. Dif(int[] numbers){ int](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-34.jpg)
Finding the smallest difference The naïve way: public static int minimal. Dif(int[] numbers){ int diff = Integer. MAX_VALUE; for(int i=0; i<numbers. length; i++){ for(int j=i+1; j<numbers. length; j++){ int current. Diff = Math. abs(numbers[i]-numbers[j]); if(current. Diff<diff){ diff = current. Diff; } } } return diff; }

Complexity of the naïve case n n The internal loop runs n-1 times, then n-2 times, then n-3 times, … As we’ve seen before , this also gives O(n 2) running time. A faster idea: Use a sorting algorithm that works in O(n·log(n)), then go over consecutive pairs only. What is the total running time this way?

Finding the smallest difference The better way: Assumes numbers is ordered in nondecreasing order. public static int minimal. Dif(int[] numbers){ int diff = Integer. MAX_VALUE; for(int i=0; i<numbers. length-1; i++){ int current. Diff = Math. abs(numbers[i]-numbers[i+1]); if(current. Diff<diff){ diff = current. Diff; } } return diff; }

Linear Search //searching for an element e in an unsorted array public static int linear. Search(int[] int. Arr, int e){ for (inti= 0; i< int. Arr. length; i++){ if (int. Arr[i]==e) return i; } Complexity: O(n), return -1; n = num of elements in the array } //we need to check each and every element till we find e. //if e is not in the array we checked n elements // (n = array length) //if the array is sorted we know when to stop searching even if the element wasn’t found
![Linear search in a sorted array public static int linear Searchint int Arr int Linear search in a sorted array public static int linear. Search(int[] int. Arr, int](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-38.jpg)
Linear search in a sorted array public static int linear. Search(int[] int. Arr, int e){ for (inti= 0; i< int. Arr. length; i++){ if (int. Arr[i]==e) { return i; } if (int. Arr[i] > e){ return -1; Complexity is still } O(n) } return -1; }

Binary Search

Binary search At the start, all of the stored values are unknown: ? ? ? ? look here first ? ? ? > > > > still unknown look here second definitely too high look here next < < < ? ? ? > > > > definitely too still unknown low definitely too high

Termination When the lower and upper bounds of the unknown area pass each other, the unknown area is empty and we terminate (unless we’ve already found the value) Goal: Locate a value, or decide it isn’t there Intentional Bound: We’ve found the value Necessary Bound: The lower and upper bounds of our search pass each other Plan: Pick a component midway between the upper and lower bounds. Reset the lower or upper bound, as appropriate.

The Binary Search Pseudocode initialize lower and upper to the lower and upper array bounds; do { set middle to (lower plus upper) / 2; if the value of data[middle] is lower set middle (plus 1) the new lower bound else set middle (minus 1) the new upper bound } while we find the value or run out of unknown data; decide why we left the loop, and return an appropriate position
![The Binary Search Java Code int binary Search int data int num The Binary Search Java Code int binary. Search (int[ ] data, int num) {](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-43.jpg)
The Binary Search Java Code int binary. Search (int[ ] data, int num) { // Binary search for num in an ordered array int middle, lower = 0, upper = (data. length - 1); do { middle = ((lower + upper) / 2); if (num < data[middle]) upper = middle - 1; else lower = middle + 1; } while ( (data[middle] != num) && (lower <= upper) ); //Postcondition: if data[middle] isn't num, no // component is if (data[middle] == num) Complexity: return middle; O(log 2 n) else return -1; }

Recursive power n n Given an integer x and a non-negative integer n, we want to compute xn What’s the recursive formula? What’s the base case? What do you think? 44

Recursive power #1 public static int power(int x, int n){ if (n == 0) { 3 = 2 return 1; 2 = 2 · 2 } 1 = 2 · 2 return x * power(x, n-1); 2 · 2 · 2 0 = } 2 · 2 · 1 = What is the runtime 8 complexity of this method? 45

Complexity of recursive methods n n When analyzing the complexity of recursive methods, we need to take into account how many recursive calls will be made (relative to the size of the input) When calculating xn, power is called n+1 times Each call takes a constant amount of time, so the runtime complexity is O(n) We can show this more formally… 46

Recursive power #1 complexity n n Let T(n) be the runtime of power(x, n) The base case takes constant time: T(0) = c For the general case, T(n) = c + T(n-1) = c + (c + T(n-2)) = 2 c + T(n-2) = 2 c + (c + T(n-3)) = 3 c + T(n-3) … Is there a pattern here? 47

Recursive power #1 complexity n n n In general, we get (for any i): T(n) = c*i + T(n-i) We would like n-i to be 0, so assign i=n: T(n) = c*n + T(0) = cn + c = O(n) Actually, this gives a lower bound too: T(n) ≥ c*n, so: T(n) = Ω(n) We could prove this by induction 48

Recursive power #1 complexity n n n Ω(f(n)) is a way of saying that an algorithm can’t be more efficient than growth rate of f(n) Lower bounds Ω(f(n)) can be used to show that an algorithm is bad (or worse than …) Upper bounds O(f(n)) can be used to show that an algorithm is good (or better than …) 49

Recursive power #1 complexity n n Don’t be confused when comparing complexity of different contexts. For recursive power #1 algorithm the runtime complexity is O(n), when n is the exponent argument of the power X^n. For insertion sort the runtime complexity is O(n^2), when n is the length of the array to sort. We should be careful when referring to n as 50 the “size” of the input.

Recursive power #1 complexity n n So for recursive power #1 algorithm we got for X^n T(n)=O(n) and T(n)= Ω(n). Can we do better? 51

Recursive power rethought n n n Recall that xa+b = xa · xb We can decompose the power n: n = 2(n / 2) + (n % 2) So we can “divide and conquer”: xn = x 2(n/2)+(n%2) = xn/2 · xn%2 52

Recursive power #2 public static int power(int x, int n){ if (n == 0) Why do we need return 1; two base cases? if (n == 1) return x; int tmp = power(x, n/2); return tmp * power(x, n%2); } Why do we use a temporary variable to store xn/2? 25 = 22· 21 = (21· 20)2· 21 = (2· 2· 1)2· 2 = 32 53

Recursive power #2 complexity n n n How many times is power called when calculating xn? Note that power(x, n%2) is always a base case (n%2 is either 0 or 1) power(x, n) is computed using one call to power(x, n/2) So the runtime complexity is O(log n) More formally… 54

Recursive power #2 complexity n n Let T(n) be the runtime of power(x, n) The base cases take constant time: T(0) = T(1) = c For the general case, T(n) = c + T(n/2) = c + (c + T(n/4)) = 2 c + T(n/4) = 2 c + (c + T(n/8)) = 3 c + T(n/8) … Is there a pattern here? 55

Recursive power #2 complexity n n In general, we get (for any i): T(n) = c*i + T(n/2 i) We would like n/2 i to be 1, so assign i = log 2(n): T(n) = c*(log n) + T(1) = c*(log n) + c = O(log n) 56

Exam questions


Common 1 – The Idea n n n We have less memory and less power (no sorting). We’ll have to work more. For every cell in the array we’ll count the number of appearances of that number. Counting will be inefficient, and we will only remember the most common number so far. Tip: Explain the algorithm you are about to use. If you get the implementation wrong you may still get some points. 59
![Solution Tip Explain and document your code public static int common 1int arr int Solution Tip: Explain and document your code public static int common 1(int[] arr){ int](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-60.jpg)
Solution Tip: Explain and document your code public static int common 1(int[] arr){ int most. Common = 0; Will hold most common int num. Appearances = 0; value found so far For every item, count the number of times it appears for(int i=0; i<arr. length; i++){ int current. Appear = count. Times(i, arr); if(current. Appear>num. Appearances){ most. Common = arr[i]; num. Appearances = current. Appear; } } Check against the current return most. Common; most common value } 60
![Counts the number of times arrindex appears from index and onwards Tip Break code Counts the number of times arr[index] appears from index and onwards. Tip: Break code](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-61.jpg)
Counts the number of times arr[index] appears from index and onwards. Tip: Break code to small manageable pieces private static int count. Times(int index, int[] arr) { int result = 1; for(int j=index+1; j<arr. length; j++){ if(arr[index]==arr[j]){ result++; } } return result; It is enough to count the number of times the item appears after the index. If it } appears before then we already covered it. 61
![A small optimization public static int common 1int arr int most Common 0 A small optimization public static int common 1(int[] arr){ int most. Common = 0;](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-62.jpg)
A small optimization public static int common 1(int[] arr){ int most. Common = 0; A small optimization: if we are close int num. Appearances=0; to the end of the array then count. Times will not be large for(int i=0; i<arr. length - num. Appearances; i++){ int current. Appear = count. Times(i, arr); if(current. Appear>num. Appearances){ most. Common = arr[i]; num. Appearances = current. Appear; } } return most. Common; } 62

Complexity n Best case: n n Tip: Do not forget to answer all parts of the question! An array with the same value (e. g. 1, 1, 1) We count the appearances of cell 0 and then stop early. O(n) running time for this input. Worst case: n n n The array {1, 2, 3, 4, 5, 6…} We count appearances of each value (n passes, then n-1, then n-2…) O(n 2) work for this input. 63

64

Common 2 n n Now we are allowed to sort. This will probably save us running time. Working on a sorted array: 1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 5, 7, 7 n n Each item appears in a consecutive segment. n We’ll use that. 65

Tip: Write a draft and then copy the code to a clean area once you are convinced it works Common 2 public static int common 2(int[] arr){ qsort(arr); int most. Common = 0; int num. Appearances=0; As before, most common value so far Marks the beginning of the current segment int segment. Start = 0; do{ int next. Segment = find. Next. Segment(segment. Start, arr); if(next. Segment-segment. Start>num. Appearances){ num. Appearances = next. Segment-segment. Start; most. Common = arr[segment. Start]; Find start of } next segment, segment. Start = next. Segment; and check the } while(segment. Start<arr. length); length of the return most. Common; People often current one } forget this 66

Complexity? n n What is the running time now? Quick. Sort takes O(n*log(n)) in the best case. O(n 2) in the worst case. Our algorithm touches every array item just once. For every segment we work in linear time in the length of the segment. n n A total of O(n) So the running time of quick sort dominates for both best and worst cases. 67

68

Common 3 n n Now we have information about the data. We can allocate an array with one cell per value, and count the number of appearances (per value) 69
![Common 3 private static int ALLOWEDVALS 100 public static int common 3int arr Common 3 private static int ALLOWED_VALS = 100; public static int common 3(int[] arr){](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-70.jpg)
Common 3 private static int ALLOWED_VALS = 100; public static int common 3(int[] arr){ int[] frequencies = new int[ALLOWED_VALS]; Count the appearances of each item for(int i=0; i<arr. length; i++){ frequencies[arr[i]]++; } Now, find the most common value int most. Common = 0; for(int i=1; i<frequencies. length; i++){ if(frequencies[most. Common]<frequencies[i]){ most. Common = i; } Tip: simulate your code } to see that it works return most. Common; 70

Complexity? n We go over the array of data once, then go over the array of frequencies once. n n The values are limited in range so the array of frequencies is of constant size! Running time is O(n). 71

![Ternary Search static int Ternaryint data int key int pivot 1 pivot 2 Ternary Search static int Ternary(int []data, int key) { int pivot 1, pivot 2,](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-73.jpg)
Ternary Search static int Ternary(int []data, int key) { int pivot 1, pivot 2, lower=0, upper=data. length-1; do { pivot 1 = (upper-lower)/3+lower; pivot 2 = 2*(upper-lower)/3+lower; if (data[pivot 1] > key){ upper = pivot 1 -1; } else if (data[pivot 2] > key){ upper = pivot 2 -1; lower = pivot 1+1; } else { lower = pivot 2+1; } } while((data[pivot 1] != key) && (data[pivot 2] != key) && (lower <= upper)); if (data[pivot 1] == key) return pivot 1; if (data[pivot 2] == key) return pivot 2; else return -1; } 73

Complexity n n Just like binary search, but instead of dividing to two, we divide to three. Same analysis as in binary search can show that the complexity is O(nlog 3 n). We note that: logan = logbn/logba Therefore O(nlog 3 n)=O(nlogn) 74
![Find Sum xyz static boolean Find Sumint data int z for int i0 i Find Sum x+y=z static boolean Find. Sum(int []data, int z){ for (int i=0; i](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-75.jpg)
Find Sum x+y=z static boolean Find. Sum(int []data, int z){ for (int i=0; i < data. length; i++){ for (int j=i+1; j<data. length; j++){ if (data[i]+data[j] == z){ System. out. println("x=" + data[i] + " and y=" + data[j]); return true; } } } return false; } How do we show the complexity? 75

Complexity n Remember the analysis for Bubble Sort: n n First loop has n iterates. Inner loop:
![Find Sum in sorted array xyz static boolean Find Sum Sortedint data int z Find Sum in sorted array x+y=z static boolean Find. Sum. Sorted(int []data, int z){](https://slidetodoc.com/presentation_image/44b7999eb19adf5b5dd250190389b2cb/image-77.jpg)
Find Sum in sorted array x+y=z static boolean Find. Sum. Sorted(int []data, int z){ int lower=0, upper=data. length-1; while ((data[lower]+data[upper] != z) && (lower < upper)) { if (data[lower]+data[upper] > z) upper--; else if (data[lower]+data[upper] < z) lower++; } if (lower >= upper) { return false; } else { System. out. println("x=" + data[lower] + " and y=" + data[upper]); } return true; Complexity? } 77