Primjena harmonijske analize na grupi rotacija Jelena Novosel




















- Slides: 24

Primjena harmonijske analize na grupi rotacija Jelena Novosel, Gordan Kreković Zagreb, siječanj 2010. Sveučilište u Zagrebu Fakultet elektrotehnike i računarstva Zavod za elektroničke sustave i obradbu informacija 1


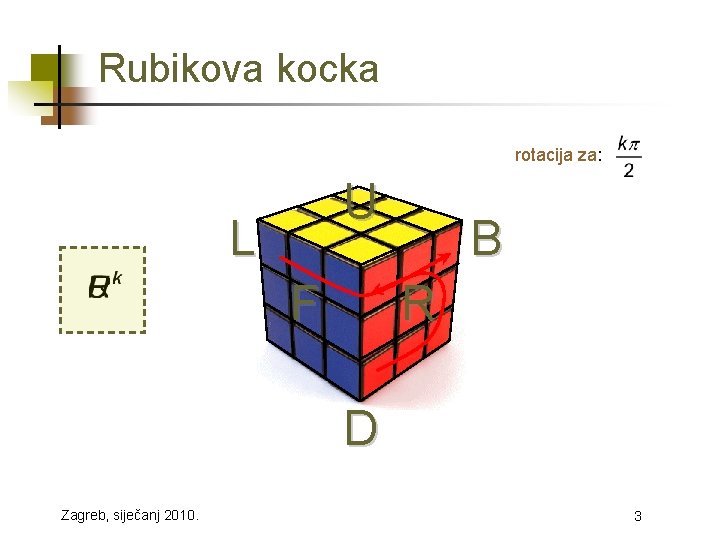
Rubikova kocka rotacija za: U L F B R D Zagreb, siječanj 2010. 3

Rubikova kocka § neutralna operacija § kompozicija: slijed operacija § nije komutativna § postoje nekomutativni elementi u skupu operacija pa se cijeli skup smatra nekomutativnim Zagreb, siječanj 2010. 4

Definicija grupe § Svojstva : skup s binarnom operacijom § grupoidnost § asocijativnost & § postojanje neutralnog elementa § postojanje inverza Zagreb, siječanj 2010. 5

Primjer grupe cijeli brojevi sa zbrajanjem § Svojstva: Zagreb, siječanj 2010. 6

Grupa rotacija SO(3) § Rotacija u trodimenzionalnom Euklidskom prostoru: § linearna transformacija § čuva duljinu vektora čiste rotacija – čuvaju orijentaciju rotacija s refleksijom Zagreb, siječanj 2010. 8

Grupa rotacija SO(3) § Uzastopna primjena rotacija je ponovno rotacija § Duljina vektora je ostala nepromijenjena posebna grupa rotacija (sadrži samo čiste rotacije) Zagreb, siječanj 2010. 9

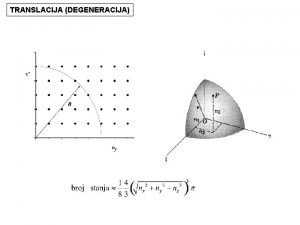
Identifikacija elementa grupe SO(3) § Neki od načina: § § § Eulerovi kutevi četvorka parametara (quartenion) osno-kutna reprezentacija kutna brzina rotacijska matrica § Za svaki je potrebno najmanje tri vrijednosti. α Zagreb, siječanj 2010. β γ 10

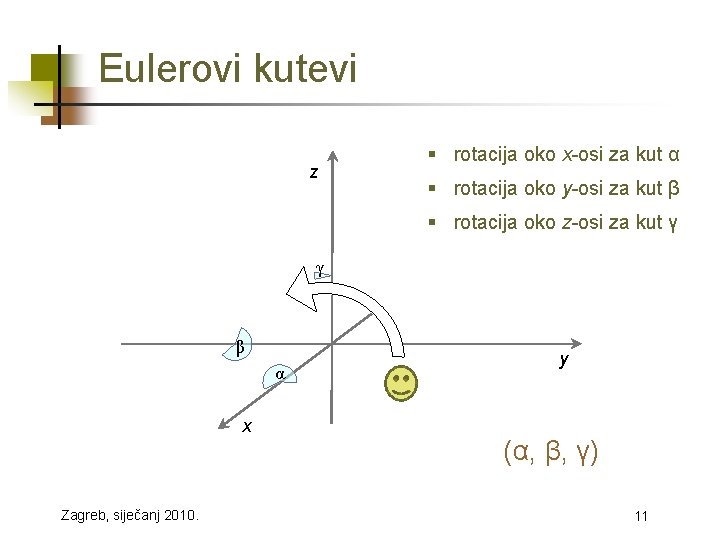
Eulerovi kutevi z § rotacija oko x-osi za kut α § rotacija oko y-osi za kut β § rotacija oko z-osi za kut γ γ β α x Zagreb, siječanj 2010. y (α, β, γ) 11

Eulerova dekompozicija § Redoslijed rotacija oko osi je važan § ukupno 6 reprezentacija koliko je i permutacija uređene trojke Ali to nije sve! § Može se pokazati da se sve 3 D rotacije mogu dobiti kombiniranjem rotacija iz samo dvije ravnine. Zagreb, siječanj 2010. 12

Eulerova dekompozicija § Jedan mogući odabir § rotacije oko z i y osi rotacija oko z osi rotacija oko y osi Zagreb, siječanj 2010. 13

Fourierova transformacija Zagreb, siječanj 2010. 14

DSOFT § Diskretna SO(3) Fourierova transformacija § integrale pretvoriti u konačne sume § funkciju uzorkovati konačnom rešetkom § Funkcija treba biti pojasno ograničena Zagreb, siječanj 2010. 15

Inverzna stereografska projekcija § Oblici inicijalno žive negdje u euklidskoj ravnini § Potrebno je ih je preslikati na sferu § Kontrakcija grupe translacija i rotacija u ravnini SE(2) u grupu rotacija u prostoru SO(3) S – južni pol T – točka na sferi T’ – stereografsk projekcija točke T Zagreb, siječanj 2010. 16

Inverzna stereografska projekcija § Cijeli slika se smješta na malu površinu blizu sjevernog pola § prednost: izobličenja proporcionalno manja § nedostatak: neučinkovita iskoristivost prostora na sferi; kompenzacija višestrukim uparivanjem Zagreb, siječanj 2010. 17

Pojasno neograničeni oblici § 6 uzoraka za demonstraciju algoritma za uparivanje § Oštri rubovi § koeficijenti vrlo visokog reda § Pojasno ograničavanje Zagreb, siječanj 2010. 18

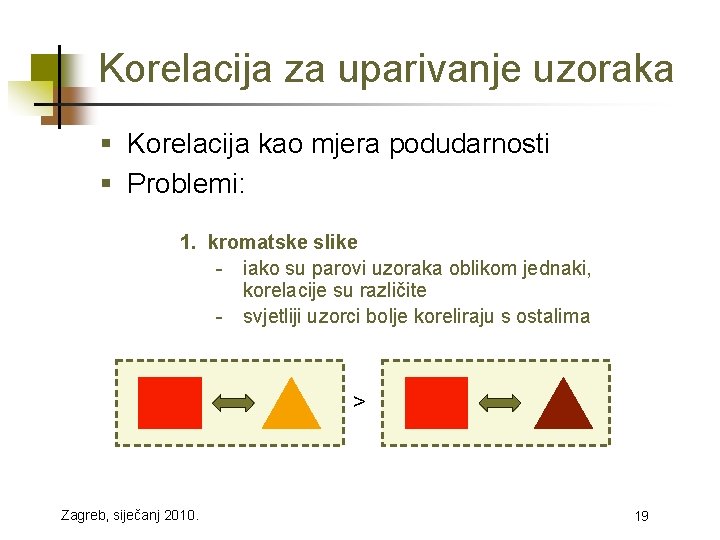
Korelacija za uparivanje uzoraka § Korelacija kao mjera podudarnosti § Problemi: 1. kromatske slike - iako su parovi uzoraka oblikom jednaki, korelacije su različite - svjetliji uzorci bolje koreliraju s ostalima > Zagreb, siječanj 2010. 19

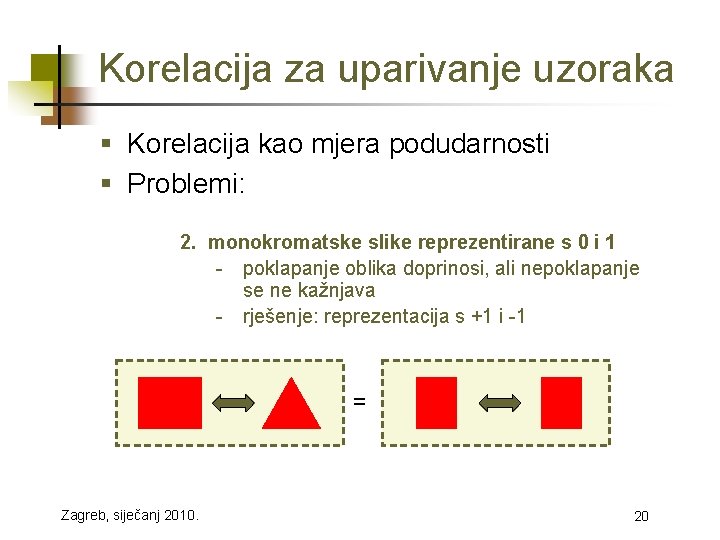
Korelacija za uparivanje uzoraka § Korelacija kao mjera podudarnosti § Problemi: 2. monokromatske slike reprezentirane s 0 i 1 - poklapanje oblika doprinosi, ali nepoklapanje se ne kažnjava - rješenje: reprezentacija s +1 i -1 = Zagreb, siječanj 2010. 20

Korelacija za uparivanje uzoraka § Dvije sfere § referentna sfera – strateški razmješteni oblici § sfera s projiciranom slikom Zagreb, siječanj 2010. 21

Korelacija za uparivanje uzoraka § Uparivanje uzoraka § sortiranje maksimuma korelacije § odlučivanje o paru iz trojke kuteva Grupiranje 200 najboljih poklapanja za svaki uzorak. Razlog podjela u grupe: simetričnost uzoraka. Zagreb, siječanj 2010. 22

Praktični rad § priprema MEX datoteke § dinamičko pozivanje funkcija napisanih u drugim programskih jezika iz Matlaba § razlog: § performanse § postojeći programski kod Zagreb, siječanj 2010. 23

Zaključak § klasična teorija Fourierove analize i konvolucije od izrazitog je značaja § prirodno je pokušati teoriju generalizirati § u primjeni najčešće grupe gibanja § nastavak istraživanja § proširiti skup uzoraka § testirati različite širine pojasa § definirati problem u više dimenzija Zagreb, siječanj 2010. 24

Završetak Hvala na pozornosti!
 Jelena novosel
Jelena novosel Dipl med techn
Dipl med techn Alkoolet projekt kimi
Alkoolet projekt kimi Gjenerata e peste e kompjuterit
Gjenerata e peste e kompjuterit Shkruani dy fjali me numeror
Shkruani dy fjali me numeror Grupi 8a
Grupi 8a Komunikacija u grupi
Komunikacija u grupi Bekim baliqi
Bekim baliqi Grupi polariseerumine
Grupi polariseerumine Vanjska rotacija nadlaktice
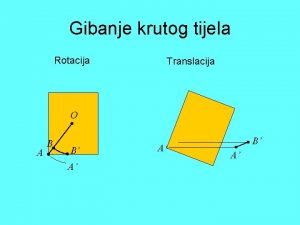
Vanjska rotacija nadlaktice Translacija i rotacija
Translacija i rotacija Senka stevanovic
Senka stevanovic Kutna akceleracija
Kutna akceleracija Mehanika krutog tijela
Mehanika krutog tijela Rotacija matematika
Rotacija matematika Primjena logaritamske funkcije
Primjena logaritamske funkcije Primijena
Primijena Zakon poluge fizika 7 zadaci
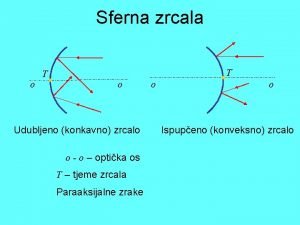
Zakon poluge fizika 7 zadaci Konkavno zrcalo
Konkavno zrcalo Dvostrana poluga
Dvostrana poluga Odnos dužina u prirodi i na karti
Odnos dužina u prirodi i na karti Primjena pitagorinog poučka na romb
Primjena pitagorinog poučka na romb Pitagorin poučak pravokutnik
Pitagorin poučak pravokutnik Kvadratna funkcija primjena
Kvadratna funkcija primjena Primjena znanstvenog zapisa u svakodnevnom životu
Primjena znanstvenog zapisa u svakodnevnom životu