7 POLUGA I PRIMJENE POLUGE ibenik 2014 2015

7 POLUGA I PRIMJENE POLUGE Šibenik, 2014. /2015.

. . . često smo u situaciji da naša mišićna sila nije dovoljna za svladavanje neke veće sile OSLONAC POLUGA – čvrsto tijelo poduprto u jednoj točki (osloncu) oko kojeg se može zakretati, a služi za savladavanje veće sile manjom silom
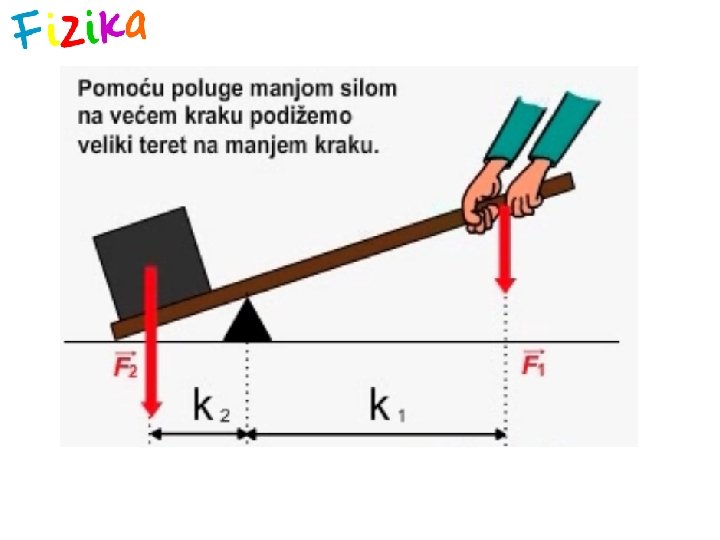
Zakon poluge „Dajte mi dovoljno dugu motku i oslonac u svemiru i podići ću Zemlju. ” Grčki matematičar i fizičar Arhimed (3. stoljeće pr. Krista) Arhimedova poluga
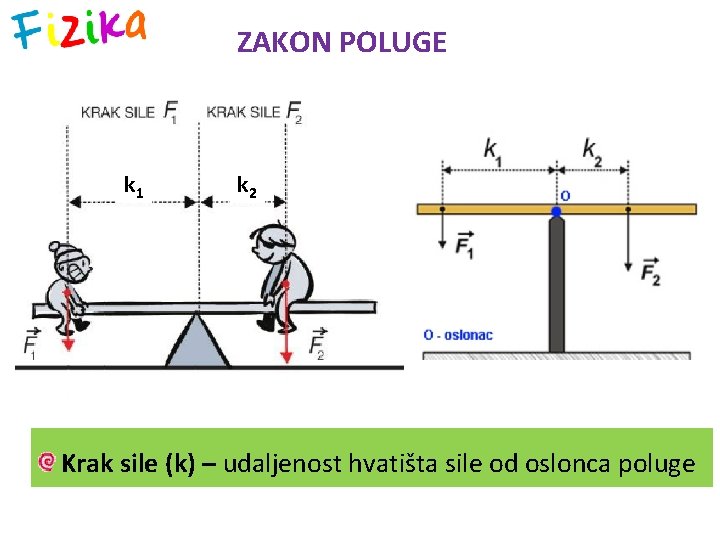
ZAKON POLUGE k 1 k 2 Krak sile (k) – udaljenost hvatišta sile od oslonca poluge
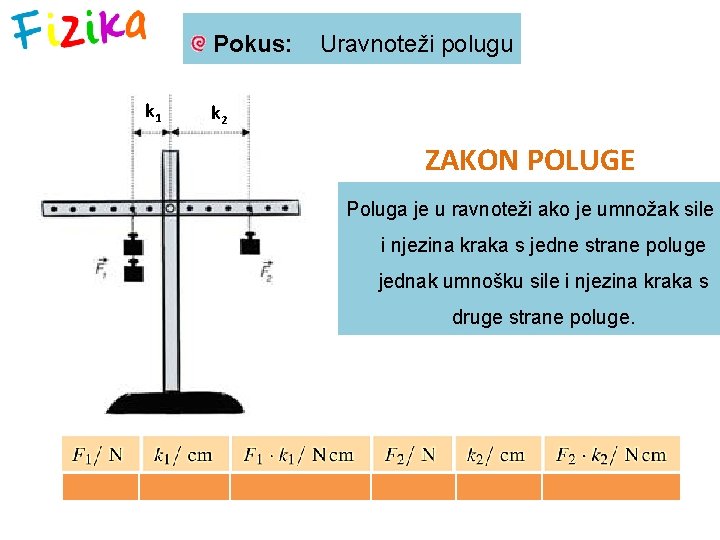
Pokus: k 1 Uravnoteži polugu k 2 ZAKON POLUGE Poluga je u ravnoteži ako je umnožak sile i njezina kraka s jedne strane poluge jednak umnošku sile i njezina kraka s druge strane poluge.
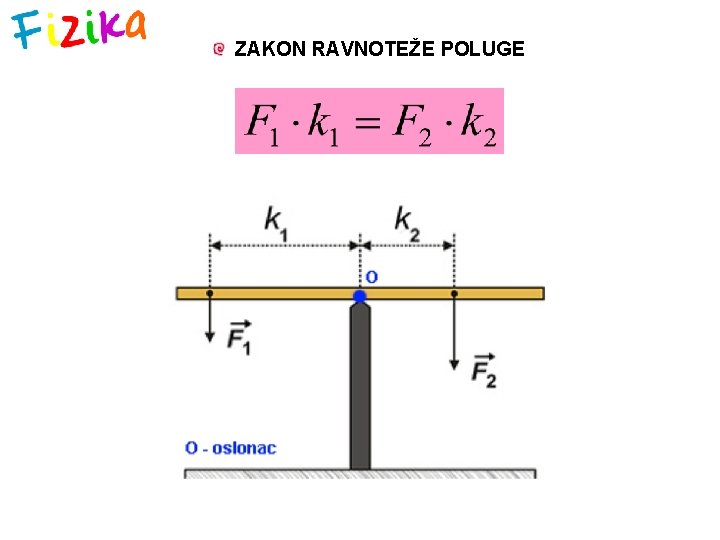
ZAKON RAVNOTEŽE POLUGE
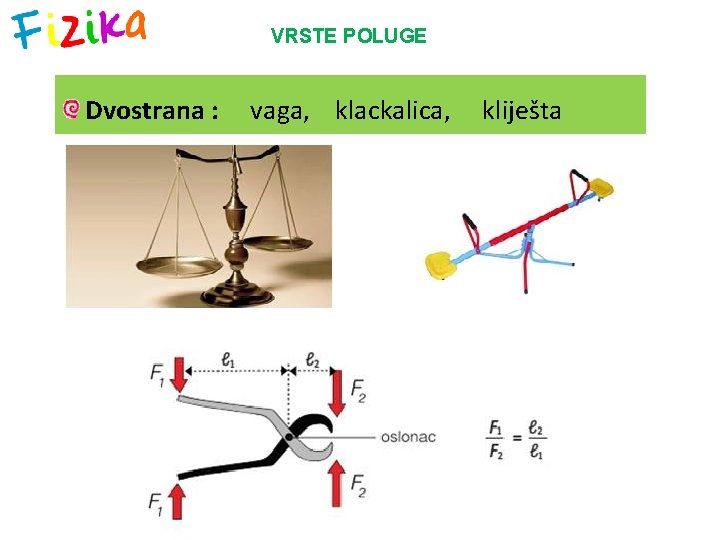
VRSTE POLUGE Dvostrana : vaga, klackalica, kliješta
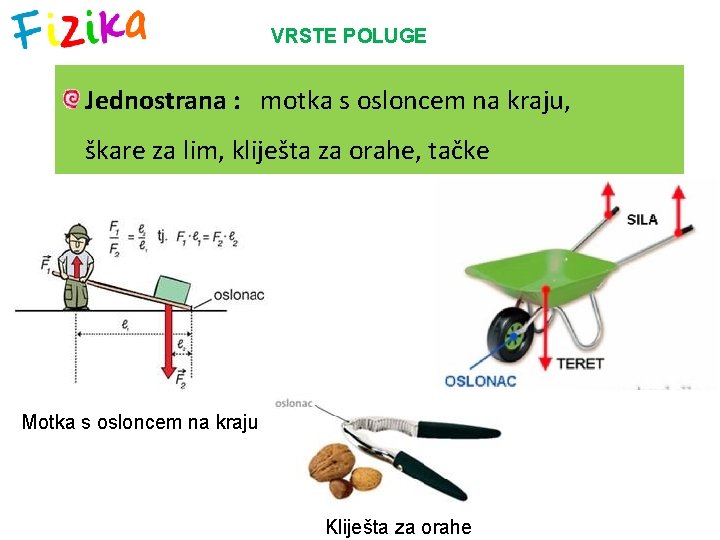
VRSTE POLUGE Jednostrana : motka s osloncem na kraju, škare za lim, kliješta za orahe, tačke Motka s osloncem na kraju Kliješta za orahe
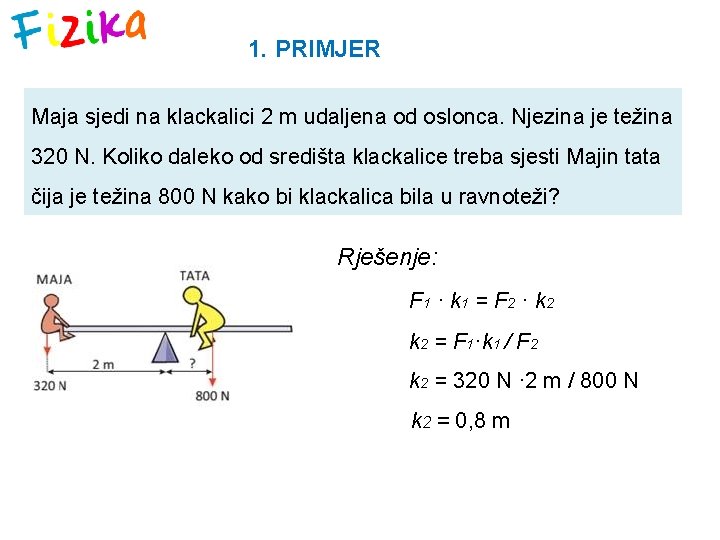
1. PRIMJER Maja sjedi na klackalici 2 m udaljena od oslonca. Njezina je težina 320 N. Koliko daleko od središta klackalice treba sjesti Majin tata čija je težina 800 N kako bi klackalica bila u ravnoteži? Rješenje: F 1 · k 1 = F 2 · k 2 = F 1·k 1 / F 2 k 2 = 320 N · 2 m / 800 N k 2 = 0, 8 m
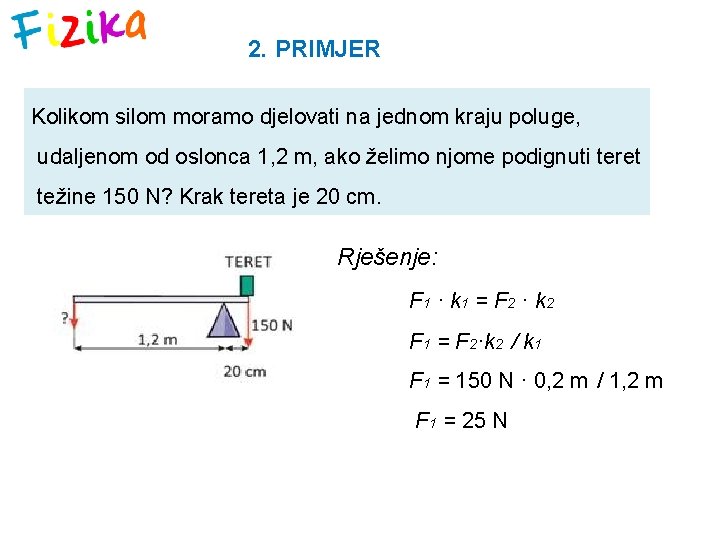
2. PRIMJER Kolikom silom moramo djelovati na jednom kraju poluge, udaljenom od oslonca 1, 2 m, ako želimo njome podignuti teret težine 150 N? Krak tereta je 20 cm. Rješenje: F 1 · k 1 = F 2 · k 2 F 1 = F 2·k 2 / k 1 F 1 = 150 N · 0, 2 m / 1, 2 m F 1 = 25 N
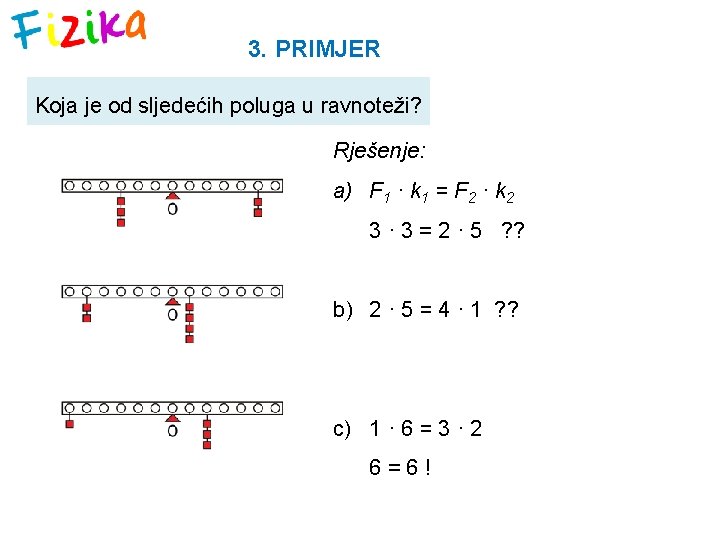
3. PRIMJER Koja je od sljedećih poluga u ravnoteži? Rješenje: a) F 1 · k 1 = F 2 · k 2 3 · 3 = 2 · 5 ? ? b) 2 · 5 = 4 · 1 ? ? c) 1 · 6 = 3 · 2 6=6!
- Slides: 12