Pitgoras Fermat y Wiles Una historia de 2500

Pitágoras, Fermat y Wiles Una historia de 2500 años

Pitágoras Siglo VI AC

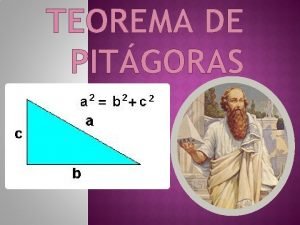
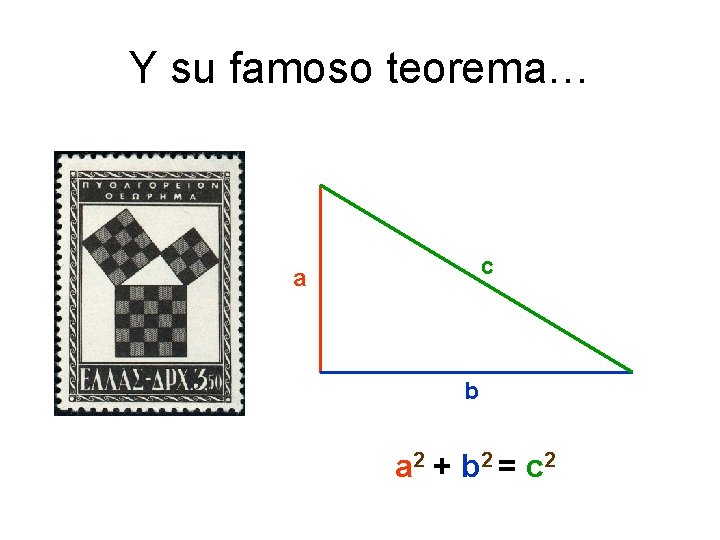
Y su famoso teorema… c a b a 2 + b 2 = c 2

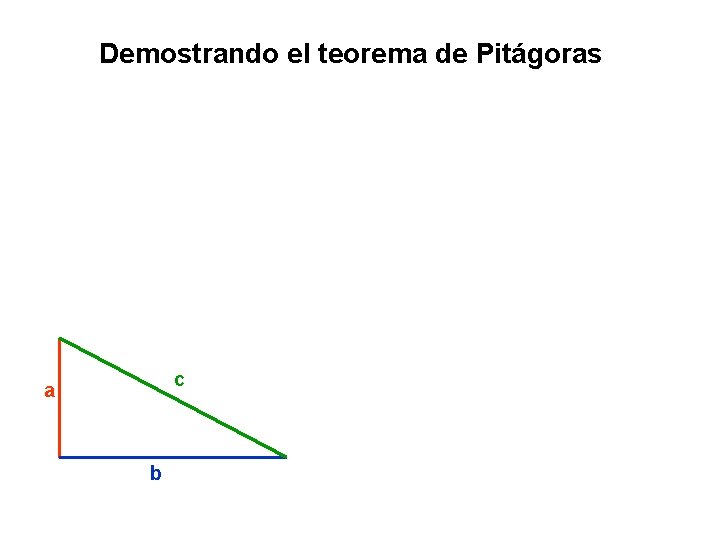
Demostrando el teorema de Pitágoras c a b

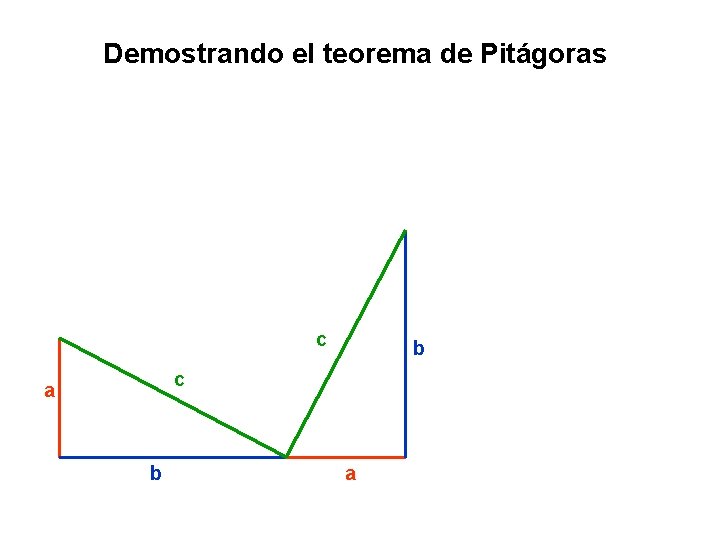
Demostrando el teorema de Pitágoras c b c a b a

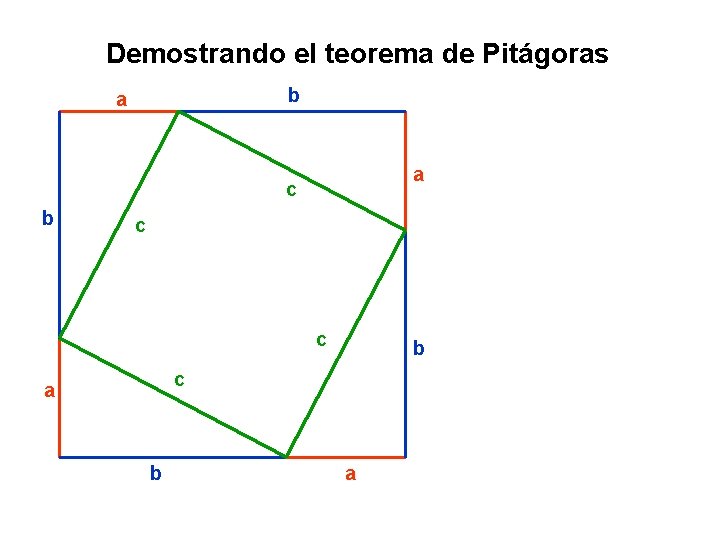
Demostrando el teorema de Pitágoras b a a c b c a b a

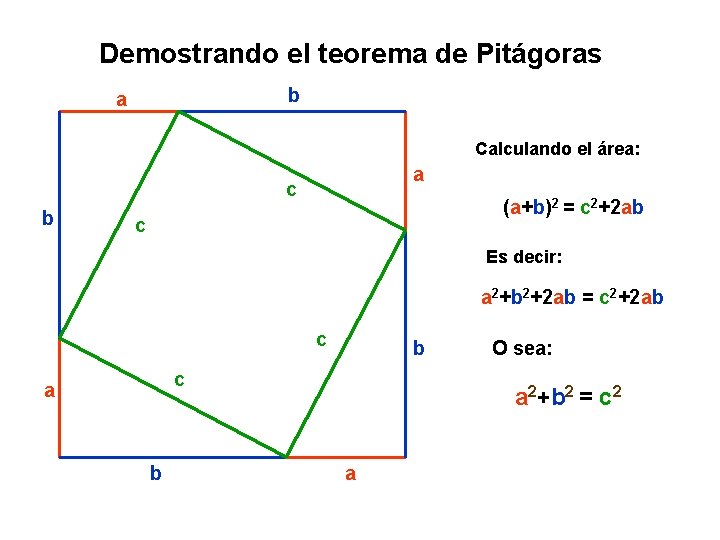
Demostrando el teorema de Pitágoras b a Calculando el área: a c b (a+b)2 = c 2+2 ab c Es decir: a 2+b 2+2 ab = c 2+2 ab c a b O sea: a 2+b 2 = c 2 a

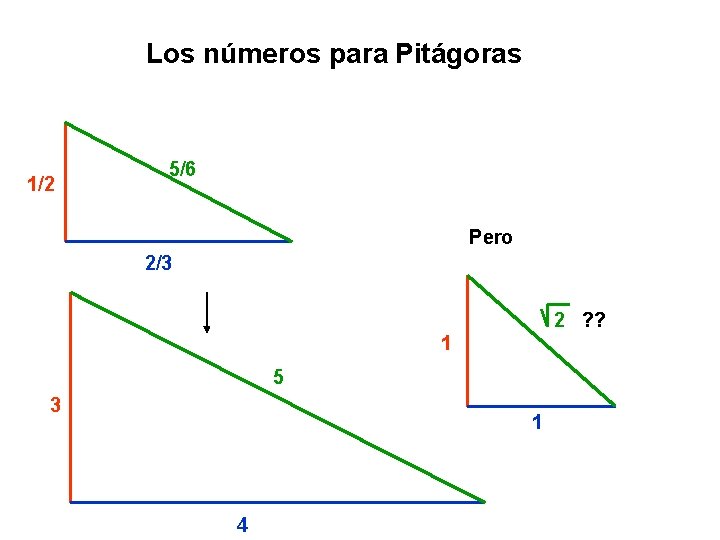
Los números para Pitágoras 1/2 5/6 Pero 2/3 2 ? ? 1 5 3 1 4

Las ternas Pitagóricas (3, 4, 5) (2. 3, 2. 4, 2. 5) (3. 3, 3. 4, 3. 5) … (k. 3, k. 4, k. 5) 32 + 42 = 52 (2. 3)2 + (2. 4)2 = (2. 5)2 (3. 3)2 + (3. 4)2 = (3. 5)2 (k. 3)2 + (k. 4)2 = (k. 5)2 Hay otras de las que son “en serio”? Sí: por ejemplo (5, 12, 13) 52 + 122 = 132

Hay muchas ternas de las que son “en serio”? Escribo todos los números: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

Hay muchas ternas de las que son “en serio”? Escribí todos los números: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Los elevo al cuadrado: 12 22 32 42 52 62 72 82 92 102 112 122 132 142 152 162 172 182 192 Lo que da: 1 4 9 16 25 36 49 64 81 100 121 144 169 194 225 256 289 324 361

Hay muchas ternas de las que son “en serio”? Escribí todos los números: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Los elevé al cuadrado: 12 22 32 42 52 62 72 82 92 102 112 122 132 142 152 162 172 182 192 Lo que dió: 1 4 9 16 25 36 49 64 81 100 121 144 169 194 225 256 289 324 361 Le resto a cada cuadrado el cuadrado anterior: 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37

Hay muchas ternas de las que son “en serio”? Escribí todos los números: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Los elevé al cuadrado: 12 22 32 42 52 62 72 82 92 102 112 122 132 142 152 162 172 182 192 Lo que dió: 1 4 9 16 25 36 49 64 81 100 121 144 169 194 225 256 289 324 361 Le resté a cada cuadrado el cuadrado anterior, y dió: 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 …

Hay muchas ternas de las que son “en serio”? Escribí todos los números: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Los elevé al cuadrado: 12 22 32 42 52 62 72 82 92 102 112 122 132 142 152 162 172 182 192 1 4 9 16 25 36 49 64 81 100 121 144 169 194 225 256 289 324 361 Le resté a cada cuadrado el cuadrado anterior, y dió: 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 3 5 7 32 11 13 15 17 19 21 23 52 27 29 31 33 35 37

Hay infinitas ternas de las que son “en serio”… 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 12 22 32 42 52 62 72 82 92 102 112 122 132 142 152 162 172 182 192 202 1 4 9 16 25 36 49 64 81 100 121 144 169 194 225 256 289 324 361 400 3 5 7 9 11 13 15 17 19 21 32 Es decir: 52 – 42 = 32 Así: 23 25 27 29 31 33 35 37 39 52 52 = 32 + 42 y 132 – 122 = 52 132 = 52 + 122 (3, 4, 5) , (5, 12, 13) , (7, 24, 25) , (9, 40, 41) , (11, 60, 61) , … Estos no son los únicos, aún más: por ejemplo (8, 15, 17) (Euclides)

Pierre de Fermat 1601 -1665

Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis ` exigitas non capere. Es imposible para un cubo escribirse como suma de dos cubos, o para una potencia cuarta escribirse como suma de dos potencias cuartas, o en general, para cualquier número igual a una potencia superior a dos escribirse como la suma de dos potencias iguales. Tengo una prueba maravillosa de este hecho pero no cabe en este margen estrecho. Pierre de Fermat, ~1937

El último teorema de Fermat No existen a , b , c tales que a 3 + b 3 = c 3, o tales que a 4 + b 4 = c 4. O más generalmente, para cualquier n>2, no existen a , b , c tales que an + b n = cn

Extendiendo los números Para resolver a 2 + b 2 = c 2, se hace a 2 = c 2 – b 2, O sea a 2 = (c - b) (c + b) = (c – 1. b) (c – ( -1. b)) Para resolver a 3 + b 3 = c 3, se hace a 3 = c 3 – b 3 y ? ? w = -1/2 + √ 3 /2 i y w 2 = -1/2 - √ 3 /2 i w Vale w 3 = 1. 1 -1 Entonces a 3 = c 3 – b 3 es lo mismo que w 2 a 3 = (c - b) (c - w b) (c – w 2 b)

Y se trabaja en el conjunto { x + y w + z w 2 } con x , y , z números enteros Pero esos conjuntos pueden ser tramposos … Por ejemplo si trabajamos en el conjunto { x + y √ 3 i } con x , y números enteros, Se tiene 4 = 2. 2 = ( 1 + √ 3 i ) ( 1 - √ 3 i ) …

Andrew Wiles 1953 – 1993/1994

Para terminar recomiendo mucho… Muchas Gracias!!!