PERSAMAAN DIFERENSIAL Definisinya Suatu persamaan yang mempunyai satu

PERSAMAAN DIFERENSIAL Definisinya : Suatu persamaan yang mempunyai satu atau lebih turunan dari sebuah fungsi yang tidak diketahui. Persamaan Umum: I. Persamaan Homogen Linear Persamaan diferensial linear orde ke –n dimana n≥ 2

Bentuk notasi operator: Ø Persamaan Linear Orde ke-2 Bentuk rumusannya: Dua asumsi penyederhanaan: 1. dan = konstanta 2. k(x) identik dengan nol

Ø Persamaan diferensial homogen linear orde ke dua Solusi dari persamaan diatas: Ø Persamaan Pelengkap dimana merupakan solusi Persamaan dalam bentuk operator: ……………. (1)

Persamaan diatas akan nol apabila: ……………(2) Persamaan(2) disebut persamaan pelengkap § Teorema A Akar-akar Real yang Berbeda Solusi Umumnya:

§ Teorema B Akar Tunggal Berulang Solusi Umumnya: § Teorema C Akar-Akar Gabungan Kompleks Akar gabungan kompleks= (α±β) Solusi Umumnya: Ø Persamaan dengan Orde yang Lebih Tinggi Akar-akar persamaan pelengkap

Contoh: Solusi umum: Contoh Soal: Tentukan solusi umum untuk: Penyelesaian:

Persamaan pelengkap: dengan akar-akar 2 i, -2 i, 1 dan -1 maka solusi umumnya II. Persamaan Tak Homogen Rumusan persamaan linear tak homogen umum: Penyelesaian Umum: 1. Solusi umum

2. Solusi khusus yp untuk tak homogen 3. Solusi Total Penyelesaian persamaan diatas mengunakan 2 metode: § Metode Koefisien Tak Tentu § Metode Variasi Parameter Ø Metode Koefisien Tak Tentu Definisi : Solusi khusus didapat dengan menduga bentuk yp jika bentuk k(x) diketahui. Bentuk k(x) polinomial, eksponensial , sinus dan cosinus

Jika k(x)= bmxm+…. +b 1 x+b 0 beαx b cos βx +c sin βx Cobalah yp = Bmxm+…. . +B 1 x+B 0 Beαx B cos βx + C sin βx Modifikasi: Jika sebuah suku di dalam fungsi k(x) merupakan solusi untuk persamaan homogen, kalikan solusi coba-coba tersebut dengan x ( atau pangkat x yang lebih tinggi ) Ilustrasi tabel diatas : 1.

2. 3. 4. 5. 6. Ø Contoh soal : Selesaikan Penyelesaian: Persamaan pelengkap akar -2 dan 1 § Solusi Umum mempunyai akar-

§ Solusi khusus : Substitusi persamaan ini ke persamaan diferensial diatas hasilnya : § Solusi Ø Metode Variasi Parameter Solusi khusus untuk persamaan tak homogen :

dimana : Contoh soal: Tentukan Solusi untuk Peny elesaian: § Solusi umum: § Solusi khusus : dimana:

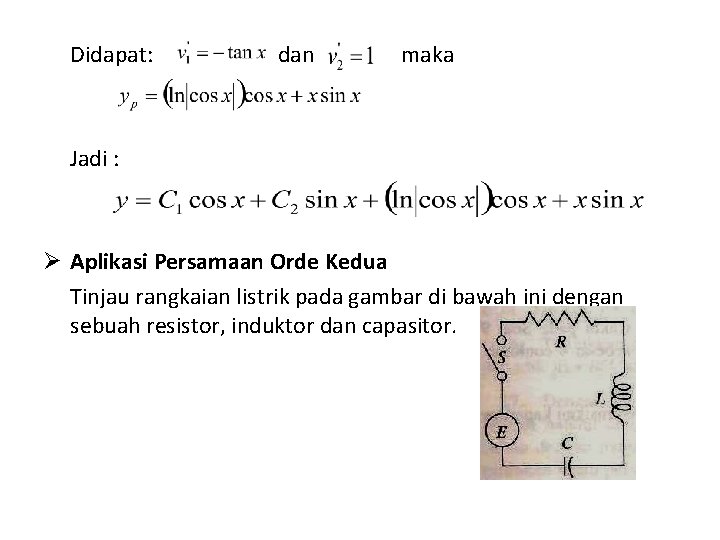
Didapat: dan maka Jadi : Ø Aplikasi Persamaan Orde Kedua Tinjau rangkaian listrik pada gambar di bawah ini dengan sebuah resistor, induktor dan capasitor.

Hukum kirchhoff dalam muatan Q (Coulomb) ……. . (1) Arus diukur dalam Amper , dan per(1) di Deferensialkan terhadap t yaitu:

Contoh : Tentukan muatan Q dan arus I sebagai fungsi-fungsi dari waktu t di dalam sebuah rangkaian RLC jika R=16 Ώ, L = 0, 02 H, C = 2 x 10 -4 F dan E = 12 V. Asumsikan Q =0 dan I = 0 di t=0 (ketika saklar tertutup) Peny: Berdasarkan hukum kirchhoff dalam rumus (1) ……. (1)

Pers pelengkap: maka: solusi khusus dari persamaan tak homogen

maka: Solusi umumnya : Syarat awal Q=0 dan I=0 pada saat t=0 maka : C 1= -2, 4 x 10 -3 I = d. Q/dt C 2= -3, 2 x 10 -3 maka:

I=d. Q/dt maka :

Pembahasan soal-soal : Selesaikan persamaan diferensial dengan koefisien tak tentu berikut ini: 1. pada x=0 2. pada x=π/3 3. 4. ketika x =0 Selesaikan PD berikut dengan variasi parameter: 5. 6. Tentukan muatan Q pada kapasitornya sebagai fungsi waktu jika S adalah rangkaian tertutup pada waktu t=0. Dimana E=1 V, R=106Ω, C=10 -6 F. Asumsikan kapasitor tersebut awalnya belum bermuatan.