1 MEKANIKA I TIM MEKANIKA PRODI FISIKA FST

1 MEKANIKA I TIM MEKANIKA PRODI FISIKA FST UNIVERSITAS JAMBI

2 GAYA BERGANTUNG KECEPATAN Hambatan Fluida dan Kecepatan Terminal kasus benda yang bergerak di dalam fluida dimana terdapat hambatan viskositas Dengan melakukan separasi variabel, maka integrasi akan menghasilkan t dan x sebagai fungsi v. integrasi kedua akan menghasilkan hubungan antara t dan x.

3

4

5 hambatan fluida termasuk gesekan udara F(v )=−c 1 v−c 2 v∣v∣=−v (c 1+c 2∣v∣) dimana c 1 dan c 2 adalah konstanta yang bergantung pada ukuran dan bentuk benda.

6 Gerak Horizontal dengan Resistansi Linier Misalkan balok dilempar dengan kecepatan awal vo pada permukaan yang smooth dan terdapat gesekan udara sehingga suku linier yang dominan. Kemudian, searah dengan gerakan Fo=0 dan F(v )=−c 1 v. Persamaan diferensial geraknya adalah Penyelesaian: Nyatakan v sebagai fungsi t dan kalikan dengan suku –c 1/m, maka dengan mudah diperoleh

7 For an object falling vertically in a resisting fluid, the force F 0 in Equations 2. 17 and 2. 18 is the weight of the object, namely, —mg for the x axis positive in the upward direction. For the linear case of fluid resistance, we then have for the differential equation of motion

8 GAYA BERGANTUNG POSISI (konsep energi kinetik dan potensial) Contoh gaya bergantung posisi adalah gaya gravitasi, gaya Coulomb, dan gaya pada pegas. Persamaan diferensial yang menggambarkan gerak lurus dari sebuah benda di bawah pengaruh gaya bergantung pada posisi adalah

9 Jika gaya tidak gayut terhadap kecepatan atau waktu, maka persamaan gerak rectilinier adalah Teorema Kerja – Energi Kinetik dimana W adalah usaha yang dilakukan partikel karena gaya F. Jadi kerja sama dengan perubahan energi kinetik partikel.

10 Jika didefinisikan fungsi V ( x) yaitu dimana V(x) adalah energi potensial, maka kerja yang dilakukan partikel Teorema Kerja – Energi Potensial

11 Jika kedua teorema digabungkan, maka yang merupakan persamaan energi, dimana E adalah energi total partikel. Persamaan ini menyatakan bahwa jika sebuah partikel bergerak di bawah pengaruh gaya bergantung posisi, kemudian penjumlahan energi kinetik dan energi potensial adalah konstan, maka gaya demikian disebut gaya konservatif. Untuk gaya non konservatif, K + V konstan, dan fungsi energi potensial tidak ada pada gaya ini. Contoh gaya non konservatif adalah gaya gesek.

12 Gerak partikel dapat peroleh dengan menyelesaikan persamaan energi tersebut, yaitu yang ditulis dengan ungkapan integral Dan diperoleh t sebagai fungsi x.

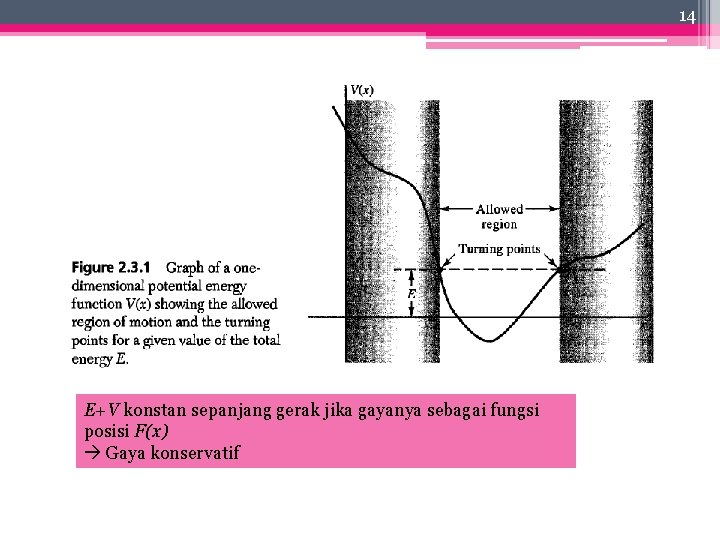
13 Dari pers. tersebut dapat dijelaskan bahwa v akan bernilai nyata apabila nilai x sedemikian rupa hingga V(x) bernilai kurang dari atau sama dengan E. Secara fisis berarti bahwa partikel tsb dibatasi pada daerah sedemikian hingga V ( x)≤E terpenuhi. Selanjutnya, jika V ( x)=0 berarti partikel dalam keadaan diam. Ini berarti partikel berhenti (diam) dan membalik gerakannya melewati titik dimana persamaan masih berlaku. Titik titik ini disebut sebagai titik balik gerakan.

14 E+V konstan sepanjang gerak jika gayanya sebagai fungsi posisi F(x) Gaya konservatif

15 Contoh: Jatuh Bebas gerak jatuh bebas adalah contoh dari gerak konservatif. Jika diambil sumbu x positif mengarah ke atas, maka gaya gravitasi sama dengan mg, sehingga d. V/dx= mg dan V=mgx + C. Jika dipilih C=0 yang berarti bahwa V=0 pada saat x=0. Persamaan energinya kemudian dimana energi total E ditentukan oleh keadaan awalnya. Misalnya, jika benda dilempar keatas dengan kecepatan awal vo dari x=o , maka sehingga Titik balik gerakan yang merupakan tinggi maksimum diperoleh dengan mensetting v=0, sehingga diperoleh

16 OSILATOR HARMONIK

17 Gerak harmonik sederhana memperlihatkan dua ciri penting: 1. Digambarkan oleh orde kedua, persamaan diferensial linear dengan koefisien konstan. Dengan demikian, prinsip superposisi dipegang; jika dua penyelesaian tertentu ditemukan, penjumlahan mereka juga sebuah penyelesaian. Kita akan melihat bukti dari contoh yang datang. 2. Periode dari gerak, atau waktu yang diperlukan untuk sebuah konfigurasi tertentu (tidak hanya posisi, tetapi kecepatan juga) untuk berulang, tidak terikat pada perpindahan maksimum dari keseimbangan.

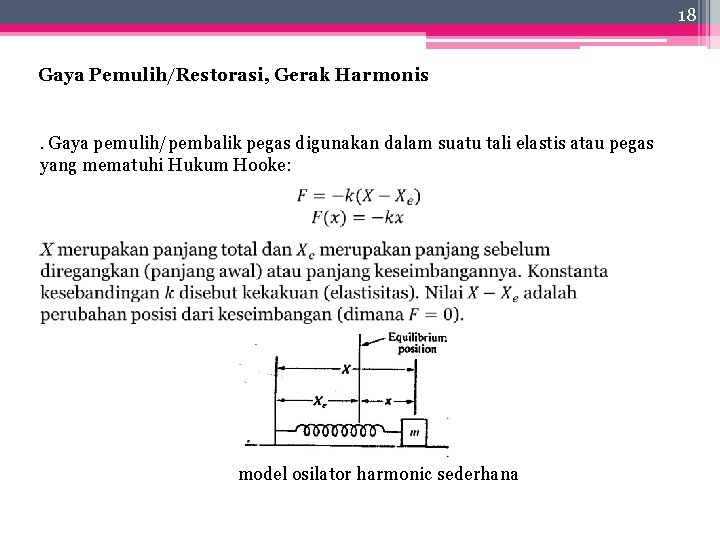
18 Gaya Pemulih/Restorasi, Gerak Harmonis . Gaya pemulih/pembalik pegas digunakan dalam suatu tali elastis atau pegas yang mematuhi Hukum Hooke: model osilator harmonic sederhana

19 Jika gaya tersebut dikenakan pada benda bermassa m, seperti pada balok di atas pada suatu permukaan horizontal tanpa gesekan solusinya adalah

20 Andaikan sebuah benda bermassa m dan pada benda itu bekerja gaya total yang berupa gaya restorasi : ΣF = − kr = −kxi − kyj − kz k, dengan k suatu tetapan positif dan r posisi benda itu. Penerapan hukum Newton menghasilkan persamaan gerak Ini adalah persamaan gerak untuk sistem mekanik yang disebut getaran selaras isotropis. Bila benda dibatasi geraknya hanya pada suatu lintasan yang hanya bergantung pada satu peubah (variable) yang menunjukkan posisinya pada suatu saat, maka diperoleh getaran selaras satu dimensi.

21 Apabila satu variabel yang dimaksud ditulis sebagai u(t), maka getaran selaras satu dimensi diwakili oleh persamaan Fungsi u(t) disebut simpangan. Solusi umum bagi persamaan diatas dengan A dan B suatu tetapan yang bergantung pada syarat awal, yakni bagaimana cara kita memberi simpangan awal.

22 Contoh Ditinjau sebuah pegas yang panjangnya l 0 (dalam keadaan rileks) yang tunduk pada hukum Hooke dengan konstanta k. Salah satu ujung pegas tersebut dihubungkan dengan sebuah balok yang bermassa m, sedang ujung yang lain dikaitkan dengan dinding sebagaimana yang diperlihatkan oleh gambar di bawah. Andaikan gesekan antara balok dengan lantai cukup kecil sehingga boleh diabaikan. Pada saat balok ditarik ke kanan sejauh x, maka pegas akan teregang dan mengerjakan gaya F pada balok yang arahnya selalu berlawanan dengan arah pergeseran balok. Jika sebagai sumbu x kita sepakati seperti pada gambar dengan titik nol berada sejauh l 0 dari dinding sebelah kiri, maka Balok hanya akan bergerak sepanjang sumbu x.

23 Solusi umum bagi persamaan diatas Andaikan mula balok ditarik sehingga berada pada titik x = x 0 dan dijaga diam di sana. Lalu pada saat t = 0 dilepaskan. Jadi, berlaku syarat awal berikut Maka diperoleh dan Jadi, B = x 0 dan A = 0. Sehingga

24 Untuk OHS, perpindahan adalah sedangkan kecepatan adalah dan nilai maksimum dari kecepatan adalah Maka energi kinetik sistem adalah dengan K 0 adalah energi kinetik maksimum dan ditulis

25 Energi potensial sistem sama dengan kerja yang dilakukan oleh gaya Fa = -F = -(-kx) = kx saat sistem berpindah dari x = 0 ke x = x. Maka dengan mensubstitusi x, diperoleh dengan V 0 adalah energi potensial maksimum saat x = A, yaitu

26 Maka energi total adalah Dari persamaan ini dapat ditentukan x(t) diperoleh solusi atau Dengan adalah dan adalah konstanta, sedangkan amplitudo

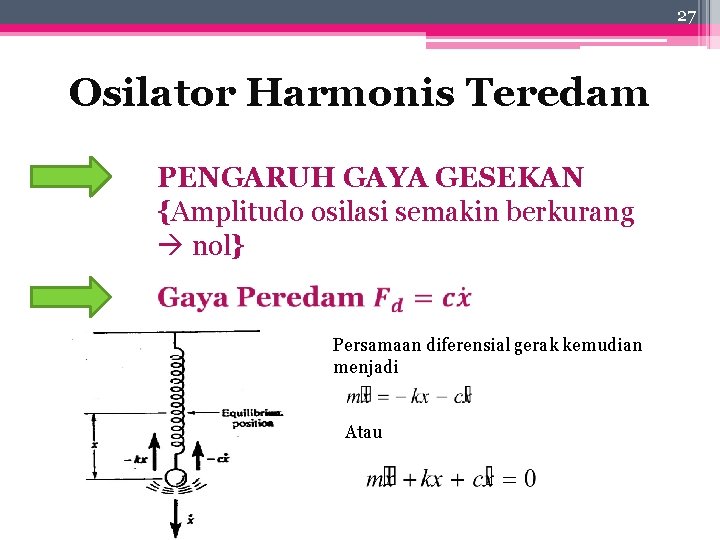
27 Osilator Harmonis Teredam PENGARUH GAYA GESEKAN {Amplitudo osilasi semakin berkurang nol} Persamaan diferensial gerak kemudian menjadi Atau

28 Apabila di samping gaya pemulih F = − kx i terdapat pula gaya peredam dan persamaan gerak

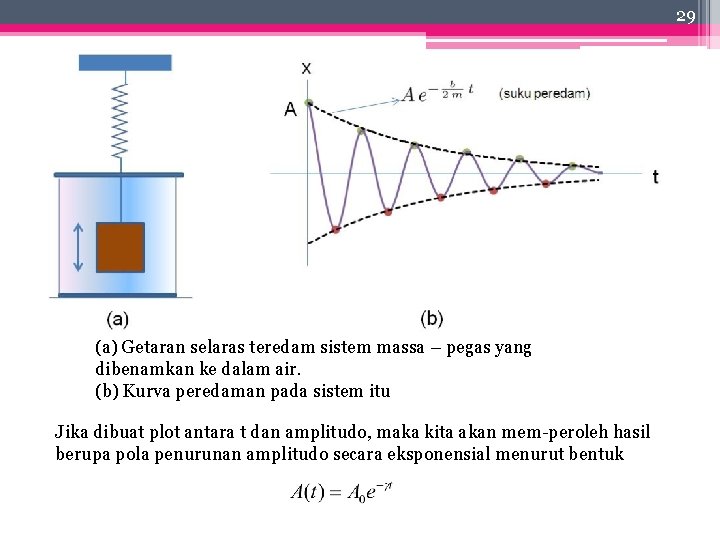
29 (a) Getaran selaras teredam sistem massa – pegas yang dibenamkan ke dalam air. (b) Kurva peredaman pada sistem itu Jika dibuat plot antara t dan amplitudo, maka kita akan mem peroleh hasil berupa pola penurunan amplitudo secara eksponensial menurut bentuk

30 Hilangkan faktor x, maka menjadi persamaan kuadrat atau disebut persamaan karakteristik :

31 Jika faktor redaman c bernilai besar, tentu akar kuadrat dalam persamaan tersebut akan bernilai real atau sebaliknya bisa menjadi imaginer. Kita ambil suku akar kuadrat D

32 Teredam tinggi

33 Solusi umum diberikan oleh Konstanta A 1 dan A 2 ditentukan dari syarat awal. Karena kedua syarat menunjukkan peluruhan/penurunan eksponensial, secara fisis gerakan juga terjadi secara exponensial dengan dua konstanta peluruhan berbeda. Dalam hal ini gaya peredam mencegah benda dari gerak bolak balik, sehingga benda menuju titik seimbang secara eksponensial tanpa mengalami gerak osilasi. grafik perpindahan dengan waktu pada kasus teredam tinggi dan teredam kritis dalam osilator harmonic.

34 Contoh Tentukan solusi umum dari persamaan OHS teredam kuat dan solusi khusus bila nilai awal x(0) = 1 dan x’(0) = 0 Solusi 1. Solusi Umum Persamaan karakteristiknya :

35 2. Solusi Khusus Substitusi nilai awal ke dalam solusi umum dan turunan pertamanya : Jadi solusi khususnya :

36 Teredam Kritis Keadaan OSH teredam kritis, mempunyai nilai akar persamaan sama, = 1 = 2 sehingga solusinya adalah : Dalam hal ini juga tidak terjadi gerak osilasi selama benda mencapai titik keseimbangan.

37 Contoh Tentukan solusi umum dari persamaan OHS teredam kritis dan solusi khusus bila nilai awal x(0) = 1 dan x’(0) = 1 Solusi 1. Solusi Umum Persamaan karakteristiknya :

38 2. Solusi Khusus Substitusi nilai awal ke dalam solusi umum dan turunan pertamanya : A=-2 dan B=1 Jadi solusi khususnya :

39 Soal Carilah solusi umum dan khusus persamaan OHS teredam berikut ini ; 1. 2.

40 Teredam Rendah Jika konstanta hambatan c cukup kecil sedemikian sehingga , kasus kita adalah teredam rendah. Dalam hal ini nilai adalah negatif, maka konsekwensi kedua q adalah angka kompleks. Jika dan . Maka

41 Solusi umum persamaan gerak kemudian dapat dinyatakan dalam kombinasi linier solusi umum dalam kaitannya dengan fungsi trigonometric Di mana konstanta C+, C , A, dan B terkait dengan cara yang sama seperti pada kasus yang tidak terendam : Dalam hal ini benda mengalami getaran dengan amplitudo semakin menyusut menuju ke titik kesetimbangan.

42 Sebagai gambaran, misalnya amplitudo pada saat t = 0 adalah bernilai satu. Kita ingin mengetahui waktu τ yang diperlukan untuk meredam hingga mencapai keadaan 1/e atau ekivalen dengan nilai 0, 37 kali amplitudo semula. Besaran ini disebut dengan waktu relaksasi. Saat t=1, kita memiliki simpangan sebesar , maka untuk keadaan yang ditanyakan berlaku Ketika redaman bertambah, τ mengecil, yang berarti bahwa proses peredaman berlang sung lebih cepat.

43 Contoh Tentukan solusi persamaan OHS teredam lemah berikut ini : Penyelesaian Persamaan karakteristiknya :

44 Osilator Harmonis Teredam Terpaksa Osilasi harmonik sederhana (OHS), adalah osilasi yang terjadi dalam suatu sistem yang hanya dipengaruhi oleh gaya konservatif yang ada padanya. disebabkan adanya gaya luar yang bekerja selain gaya konservatifnya, yaitu gaya redaman yang selalu melawan arah gerak beban.

45 Sebagai contoh seorang anak TK yang sedang main ayunan lama kelamaan ayunannya akan berhenti. Tetapi bila sang ibu selalu mendorongnya manakala ayunan si anak sampai kedirinya, maka ayunan anak itu akan berlangsung terus menerus. Dalam kasus yang dikatakan ayunan anak lebih dominan disebabkan oleh gaya dorongan sang ibu. Dengan kata lain sistem (dalam hal ini anak itu) dipaksa berosilasi oleh gaya luar yang menggeraknya. Osilasi semacam ini dinamakan osilasi terpaksa.

46 Gaya total yang digunakan merupakan penjumlahan tiga gaya: gaya pemulih/pembalik elastis –kx, gaya peredaman kekentalan (gaya gesek) dan gaya penggerak / gaya pemaksa / gaya luar Maka Persamaan differensial dari gerak tersebut dimana Fext berubah secara sinusoidal terhadap waktu.

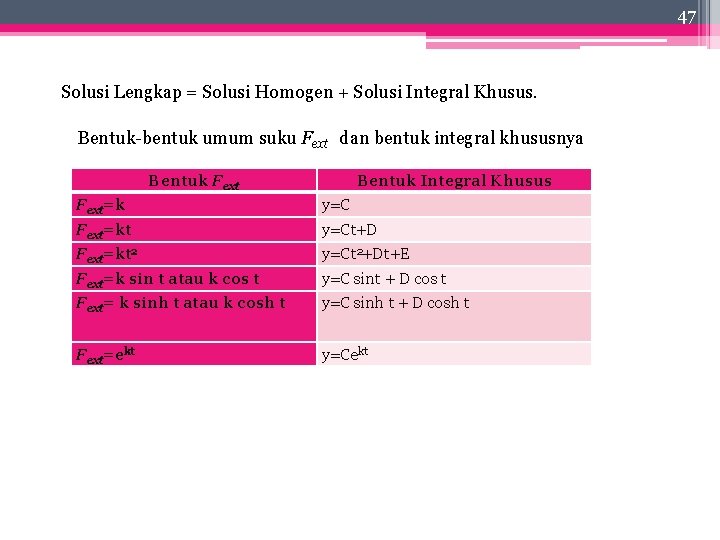
47 Solusi Lengkap = Solusi Homogen + Solusi Integral Khusus. Bentuk bentuk umum suku Fext dan bentuk integral khususnya Bentuk Fext Bentuk Integral Khusus Fext=k y=C Fext=kt y=Ct+D Fext=kt 2 y=Ct 2+Dt+E Fext=k sin t atau k cos t y=C sint + D cos t Fext= k sinh t atau k cosh t y=C sinh t + D cosh t Fext=ekt y=Cekt

48 Contoh Tentukan solusi persamaan OHS berikut ini : Penyelesaian Solusi Homogen : Solusi homogennya menjadi Solusi Integral Khusus Untuk memperoleh integral khususnya, kita gunakan bentuk umum ruas kanan yaitu fungsi berderajat dua. Misalkan y=Ct 2+Dt+E maka

49 Subtitusikan ke dalam persamaan awal, kita peroleh : 2 C – 5(2 Ct+D) + 6(Ct 2+Dt+E)=t 2 2 C – 10 Ct – 5 D + 6 Ct 2 + 6 Dt + 6 E = t 2 6 Ct 2 + (6 D – 10 C)t + (2 C – 5 D + 6 E) = t 2 Dengan menyamakan koefisien dari t yang berpangkat sama, kita dapatkan : t 2 ------ 6 C = 1 t ------ 6 D-10 C =0 2 C-5 D+6 E=0 maka C=1/6 maka D=5/18 maka E=19/108

50 Jadi solusi integral khususnya adalah Solusi lengkapnya :

51 Soal Tentukan solusi dari :