Diferensial Fungsi Majemuk Diferensial Parsial Diferensial Total Chain

Diferensial Fungsi Majemuk -Diferensial Parsial - Diferensial Total - Chain rule - dll

Diferensial Parsial Diferensial Total

High Order Partial Derivatives Fungsi dengan lebih dari satu variabel bebas juga dapat diturunkan lebih dari satu kali Turunan parsial z = f (x, y) kalau kontinyu dapat mempunyai turunannya sendiri. empat turunan parsial : • Dapat dilambangkan fxx, fxy, fyx, dan fyy • fxy = fyx

Partial derivatives Cobb-Douglas Q = 96 K 0. 3 L 0. 7 production function ( + =1)

�Market model Techniques of partial differentiation

• Market model Geometric interpretation of partial derivatives

• Market model

Q Q S 0 S S 1 D P D P

S 1 Q Q S 0 D P Q 0 Q 1 D 0 P Market model

Y = C + I 0 + G 0 C = a + b(Y-T); T=d+t. Y; b = MPC t = MPT Y=( a-bd+I+G)/(1 -b+tb) C=(b(1 -t)(I+G)+a-bd)/ (1 -b+tb) T=(t(I+G)+ta+d(1 -b))/ (1 -b+tb) National-income model (a > 0; 0 < b < 1) (d > 0; 0 < t < 1)

Input-output model ∂x 1/∂d 1 = b 11

�Use Jacobian determinants to test the existence of functional dependence between the functions /J/ �Not limited to linear functions as /A/ (special case of /J/ �If /J/ = 0 then the non-linear or linear functions are dependent and a solution does not exist. Note on Jacobian Determinants

Total Differentials

Diferensial Total

Let Utility function U = U (x 1, x 2, …, xn) Differentiation of U wrt x 1. . n U/ xi is the marginal utility of the good xi dxi is the change in consumption of good xi

• Given a function y = f (x 1, x 2, …, xn) • Total differential dy is: • Total derivative of y with respect to x 2 found by dividing both sides by dx 2 (partial total derivative) Finding the total derivative from the differential

Chain rule (kaidah rantai) � This is a case of two or more differentiable functions, in which each has a distinct independent variable. where z = f(g(x)), i. e. , z = f(y), i. e. , z is a function of variable y and • y If=Rg(x), = f(Q)i. e. , and ify Q is =a g(L) function of variable x

z x Kaidah Rantai y t Pohon rantai

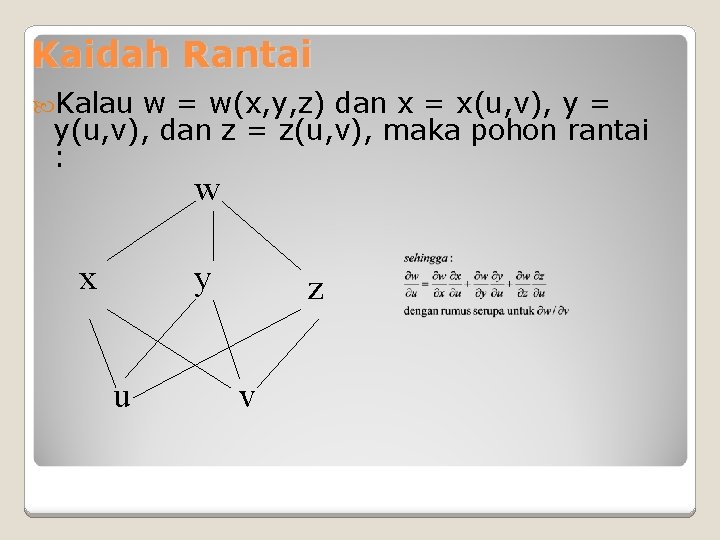
Kaidah Rantai Kalau w = w(x, y, z) dan x = x(u, v), y = y(u, v), dan z = z(u, v), maka pohon rantai : w x y u z v

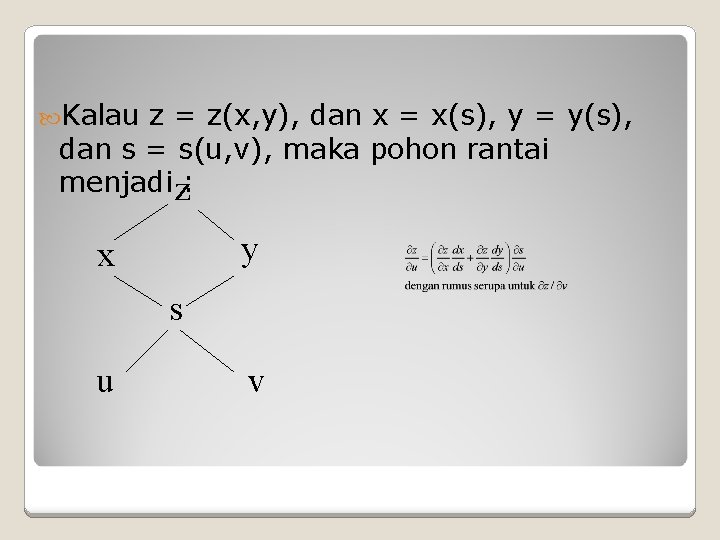
Kalau z = z(x, y), dan x = x(s), y = y(s), dan s = s(u, v), maka pohon rantai menjadi z: y x s u v