PDE Methods are Not Necessarily Level Set Methods

PDE Methods are Not Necessarily Level Set Methods Allen Tannenbaum Georgia Institute of Technology Emory University 1

PDE Methods in Computer Vision and Imaging q. Image Enhancement q. Segmentation q. Edge Detection q. Shape-from-Shading q. Object Recognition q. Shape Theory q. Optical Flow q. Visual Tracking q. Registration 2

Scale in Biological Systems 3

Micro/Macro Models-Scale I 4

Micro/Macro Models-Scale II 5

How to Move Curves and Surfaces q. Parameterized Objects: methods dominate control and visual tracking; ideal for filtering and state space techniques. q. Level Sets: implicitly defined curves and surfaces. Several compromises; narrow banding, fast marching. q. Minimize Directly Energy Functional: conjugate gradient on triangulated surface (Ken Brakke). 6

Level Sets-A History Independently: Peter Olver (1976), Ph. D. thesis Sigurd Angenent (Leiden University Report, 1982) Mathematical Justification: Chen-Giga-Goto (1991) Evans and Spruck (1991) 7

When Do They Work 8

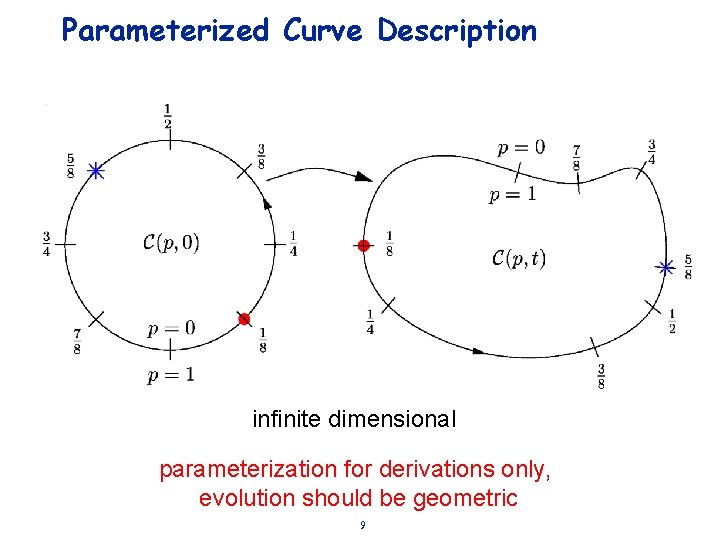
Parameterized Curve Description infinite dimensional parameterization for derivations only, evolution should be geometric 9

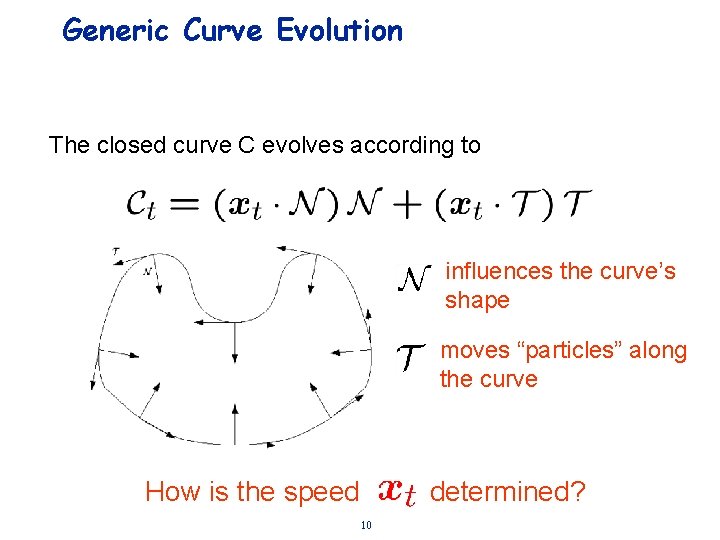
Generic Curve Evolution The closed curve C evolves according to influences the curve’s shape moves “particles” along the curve How is the speed 10 determined?

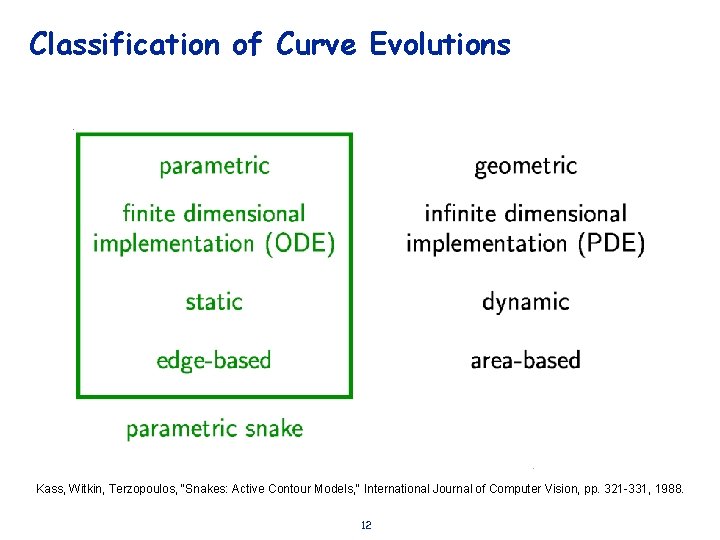
Classification of Curve Evolutions 11

Classification of Curve Evolutions Kass, Witkin, Terzopoulos, "Snakes: Active Contour Models, " International Journal of Computer Vision, pp. 321 -331, 1988. 12

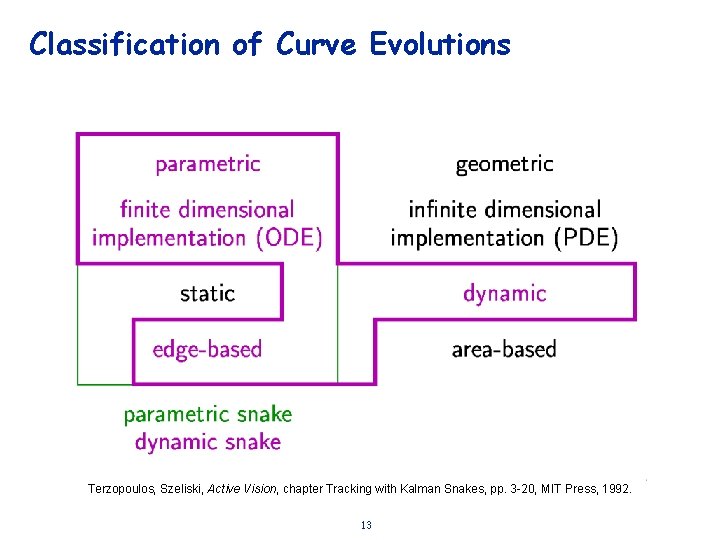
Classification of Curve Evolutions Terzopoulos, Szeliski, Active Vision, chapter Tracking with Kalman Snakes, pp. 3 -20, MIT Press, 1992. 13

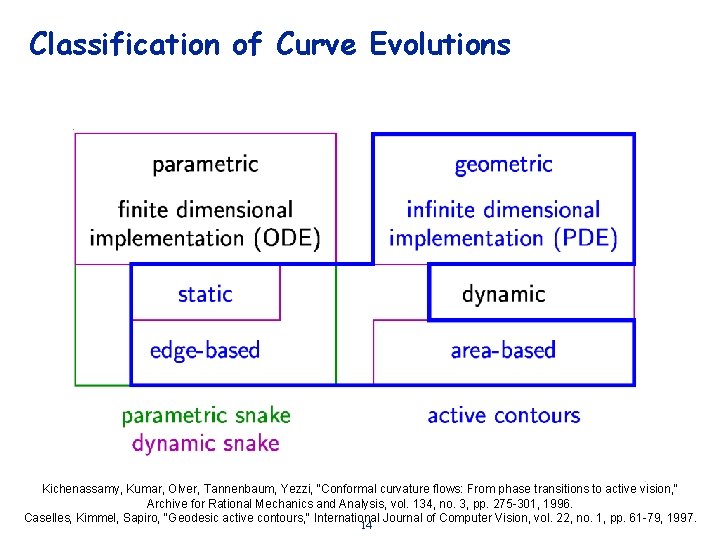
Classification of Curve Evolutions Kichenassamy, Kumar, Olver, Tannenbaum, Yezzi, "Conformal curvature flows: From phase transitions to active vision, " Archive for Rational Mechanics and Analysis, vol. 134, no. 3, pp. 275 -301, 1996. Caselles, Kimmel, Sapiro, "Geodesic active contours, " International Journal of Computer Vision, vol. 22, no. 1, pp. 61 -79, 1997. 14

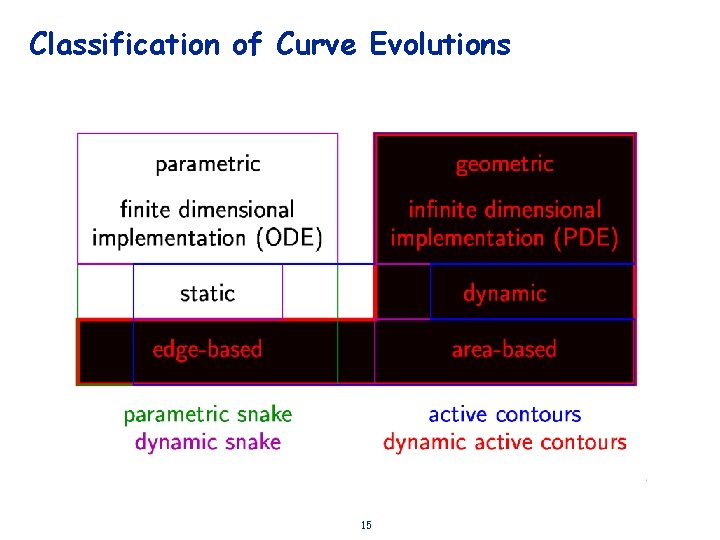
Classification of Curve Evolutions 15

Static Approaches Minimize using the functionals Kass snake (parametric) Geodesic active contour (geometric) 16

Static Approaches Minimizing leads to the Euler-Lagrange equations Kass snake (parametric) Geodesic active contour (geometric) 17

Static Approaches Minimizing results in the gradient descent flow Kass snake (parametric) Geodesic active contour (geometric) is an artificial time parameter 18

Dynamic Approach Minimize the action integral where is the Lagrangian, is the kinetic energy and is the potential energy. 19

Dynamic Approach Minimizing using the functional Terzopoulos and Szeliski (parametric) 20

Dynamic Approach Minimizing results in the Euler-Lagrange equation Terzopoulos and Szeliski (parametric) Here, is physical time 21

Dynamic Approach Minimizing results in the Euler-Lagrange equation Terzopoulos and Szeliski (parametric) But what about a geometric formulation? 22

Geometric Dynamic Approach Minimize using the Lagrangian results in the Euler-Lagrange equation 23

Geometric Dynamic Approach We can write We then obtain the following two coupled PDEs for the tangential and the normal velocities: The tangential velocity matters. 24

PDE’s Without Level Sets: Some Examples 25

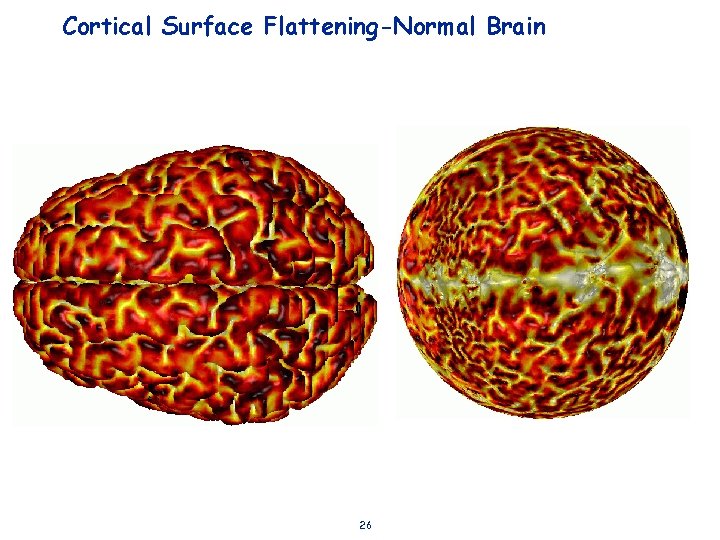
Cortical Surface Flattening-Normal Brain 26

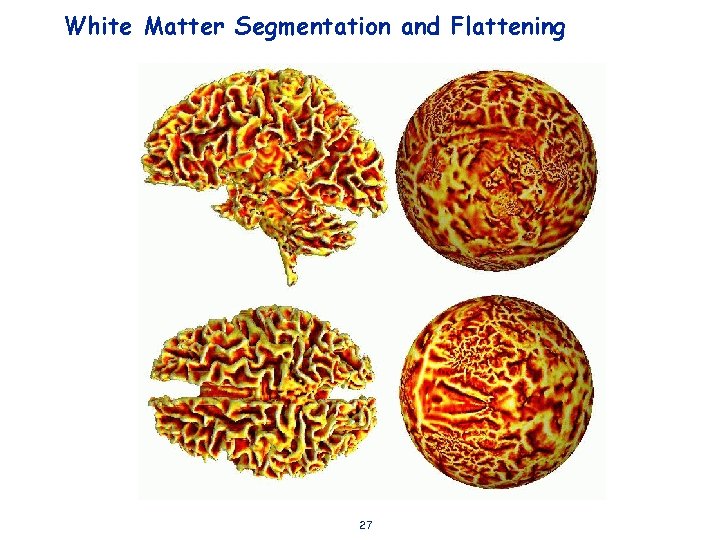
White Matter Segmentation and Flattening 27

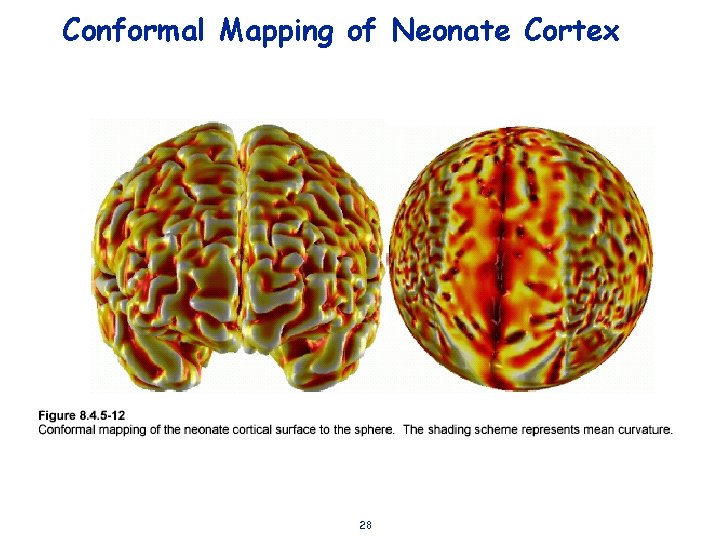
Conformal Mapping of Neonate Cortex 28

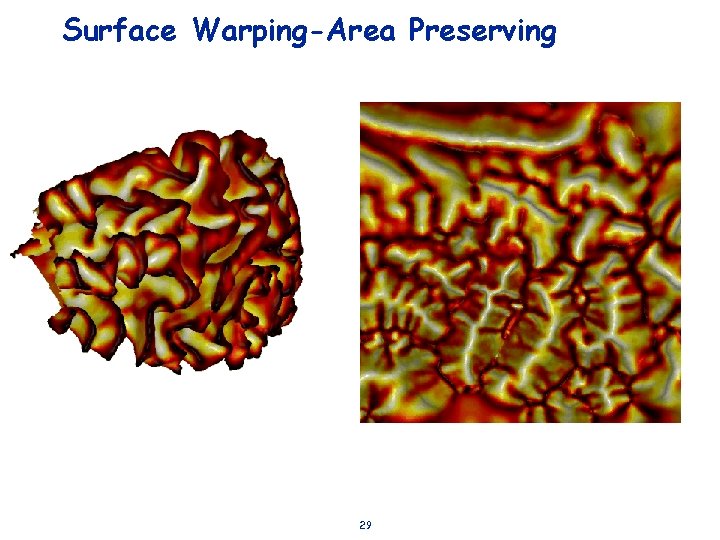
Surface Warping-Area Preserving 29

Flame Morphing 30

Anisotropic active contours • Add directionality 31

Curve minimization q. Calculus of variations l Start with initial curve l Deform to minimize energy l Steady state is locally optimum Registration, Atlas-based segmentation q. Dynamic programming l Choose seed point s l For any point t, determine globally optimal curve t s 32 Segmentation

Synthetic example (3 D) 33

Stochastic Approximations 34

Curvature Driven Flows 35

Euclidean and Affine Flows 36

Euclidean and Affine Flows 37

Birth/Death Zero Range Processes-I q. S: discrete torus TN, W=N q. Particle configuration space: N q. Markov generator: 38 T N

Birth/Death Zero Range Processes-II q. Markov generator: 39

Birth/Death Zero Range Process-III q. Markov generator: q Each particle configuration defines a positive measure on the un q To make the curve zero barycenter, a corrected measure is use q Reconstruct the curve with: 40

The Tangential Component is Important 41

Nonconvex Curves 42

Stochastic Interpretation-I 43

Stochastic Interpretation-II 44

Stochastic Interpretation-III 45

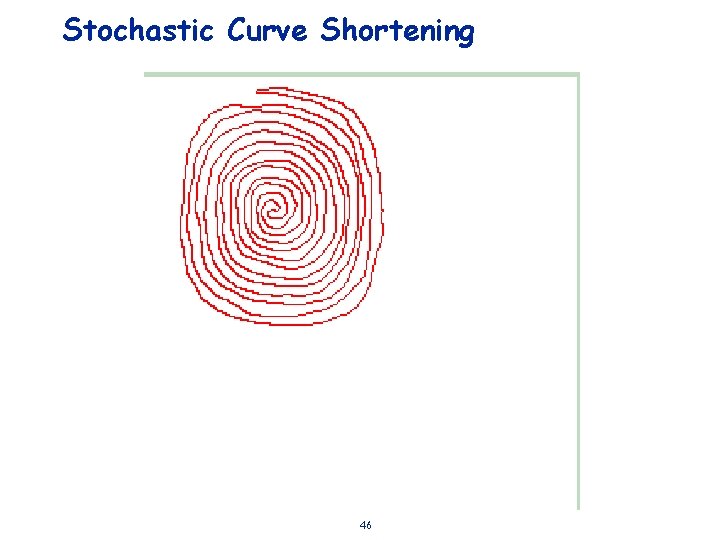
Stochastic Curve Shortening 46

Conclusions q. Level sets are a way of implementing curvature driven flows. q. Loss of information. q. Modifications are necessary. q. Do not work if no maximum principle. q. Combination with other methods, e. g. Bayesian. 47