SE 301 Numerical Methods Topic 9 Partial Differential

SE 301: Numerical Methods Topic 9 Partial Differential Equations (PDEs) Lectures 37 -39 KFUPM Read 29. 1 -29. 2 & 30. 1 -30. 4 CISE 301_Topic 9 KFUPM 1

Lecture 37 Partial Differential Equations p p CISE 301_Topic 9 Partial Differential Equations (PDEs). What is a PDE? Examples of Important PDEs. Classification of PDEs. KFUPM 2

Partial Differential Equations A partial differential equation (PDE) is an equation that involves an unknown function and its partial derivatives. CISE 301_Topic 9 KFUPM 3

Notation CISE 301_Topic 9 KFUPM 4

Linear PDE Classification CISE 301_Topic 9 KFUPM 5

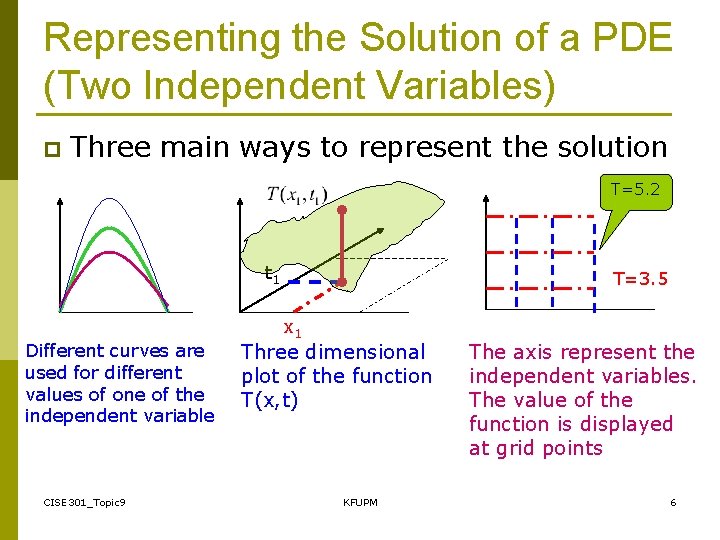
Representing the Solution of a PDE (Two Independent Variables) p Three main ways to represent the solution T=5. 2 t 1 Different curves are used for different values of one of the independent variable CISE 301_Topic 9 T=3. 5 x 1 Three dimensional plot of the function T(x, t) KFUPM The axis represent the independent variables. The value of the function is displayed at grid points 6

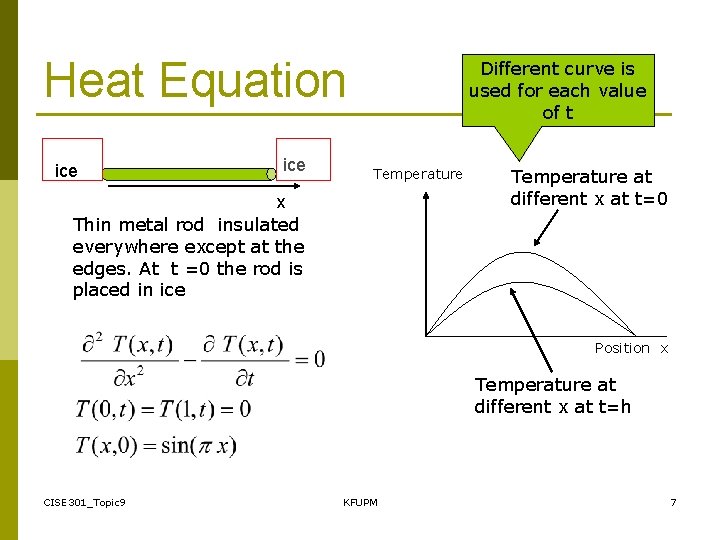
Heat Equation ice Different curve is used for each value of t Temperature x Thin metal rod insulated everywhere except at the edges. At t =0 the rod is placed in ice Temperature at different x at t=0 Position x Temperature at different x at t=h CISE 301_Topic 9 KFUPM 7

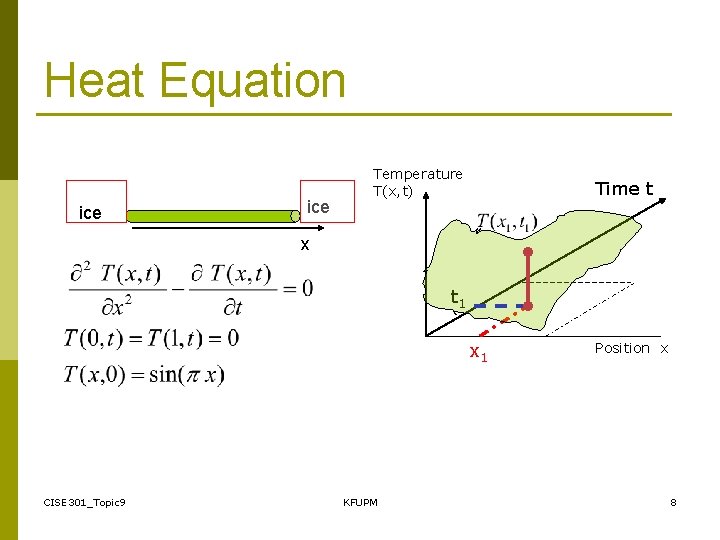
Heat Equation ice Temperature T(x, t) Time t x t 1 x 1 CISE 301_Topic 9 KFUPM Position x 8

Linear Second Order PDEs Classification CISE 301_Topic 9 KFUPM 9

Linear Second Order PDE Examples (Classification) CISE 301_Topic 9 KFUPM 10

Classification of PDEs Linear Second order PDEs are important sets of equations that are used to model many systems in many different fields of science and engineering. Classification is important because: n n Each category relates to specific engineering problems. Different approaches are used to solve these categories. CISE 301_Topic 9 KFUPM 11

Examples of PDEs are used to model many systems in many different fields of science and engineering. Important Examples: n n Wave Equation Heat Equation Laplace Equation Biharmonic Equation CISE 301_Topic 9 KFUPM 12

Heat Equation The function u(x, y, z, t) is used to represent the temperature at time t in a physical body at a point with coordinates (x, y, z). CISE 301_Topic 9 KFUPM 13

Simpler Heat Equation x u(x, t) is used to represent the temperature at time t at the point x of the thin rod. CISE 301_Topic 9 KFUPM 14

Wave Equation The function u(x, y, z, t) is used to represent the displacement at time t of a particle whose position at rest is (x, y, z). Used to model movement of 3 D elastic body. CISE 301_Topic 9 KFUPM 15

Laplace Equation Used to describe the steady state distribution of heat in a body. Also used to describe the steady state distribution of electrical charge in a body. CISE 301_Topic 9 KFUPM 16

Biharmonic Equation Used in the study of elastic stress. CISE 301_Topic 9 KFUPM 17

Boundary Conditions for PDEs To uniquely specify a solution to the PDE, a set of boundary conditions are needed. p Both regular and irregular boundaries are possible. t p region of interest x 1 CISE 301_Topic 9 KFUPM 18

The Solution Methods for PDEs p Analytic solutions are possible for simple and special (idealized) cases only. p To make use of the nature of the equations, different methods are used to solve different classes of PDEs. p The methods discussed here are based on the finite difference technique. CISE 301_Topic 9 KFUPM 19

Lecture 38 Parabolic Equations p p p CISE 301_Topic 9 Parabolic Equations Heat Conduction Equation Explicit Method Implicit Method Cranks Nicolson Method KFUPM 20

Parabolic Equations CISE 301_Topic 9 KFUPM 21

Parabolic Problems ice x CISE 301_Topic 9 KFUPM 22

First Order Partial Derivative Finite Difference Central Difference Method CISE 301_Topic 9 Forward Difference Method KFUPM Backward Difference Method 23

Finite Difference Methods CISE 301_Topic 9 KFUPM 24

Finite Difference Methods New Notation Superscript for t-axis and Subscript for x-axis Til-1=Ti, j-1=T(x, t-∆t) CISE 301_Topic 9 KFUPM 25

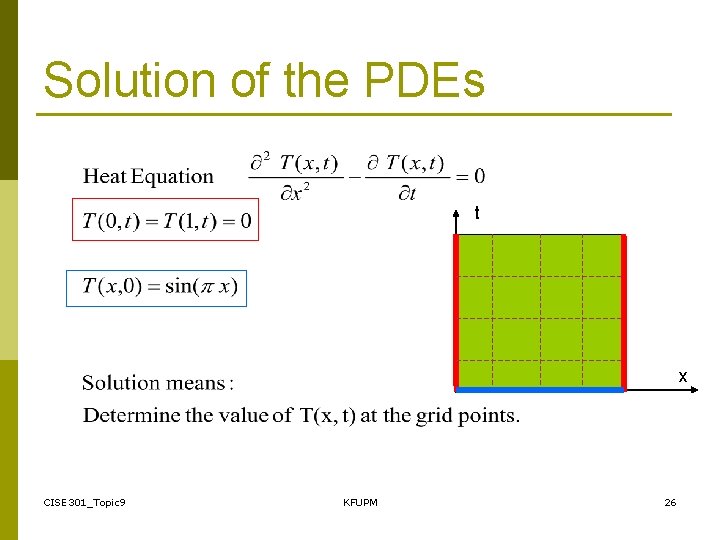
Solution of the PDEs t x CISE 301_Topic 9 KFUPM 26

Solution of the Heat Equation • Two solutions to the Parabolic Equation (Heat Equation) will be presented: 1. Explicit Method: Simple, Stability Problems. 2. Crank-Nicolson Method: Involves the solution of a Tridiagonal system of equations, Stable. CISE 301_Topic 9 KFUPM 27

Explicit Method CISE 301_Topic 9 KFUPM 28

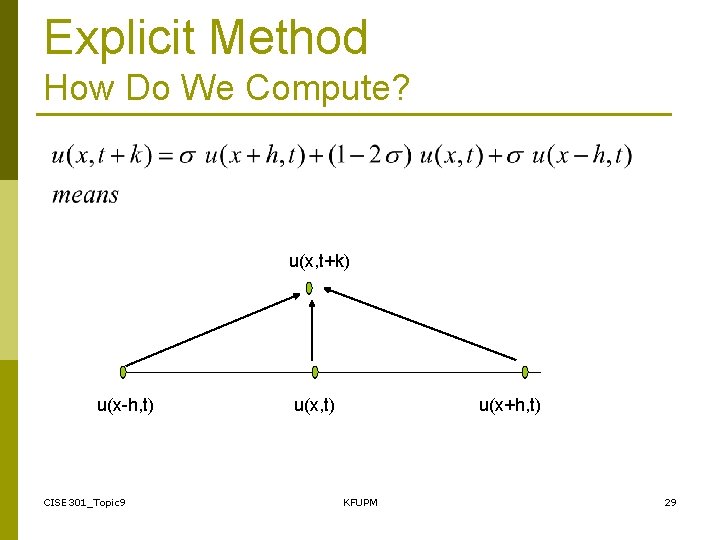
Explicit Method How Do We Compute? u(x, t+k) u(x-h, t) CISE 301_Topic 9 u(x, t) u(x+h, t) KFUPM 29

Explicit Method How Do We Compute? CISE 301_Topic 9 KFUPM 30

Explicit Method CISE 301_Topic 9 KFUPM 31

Crank-Nicolson Method CISE 301_Topic 9 KFUPM 32

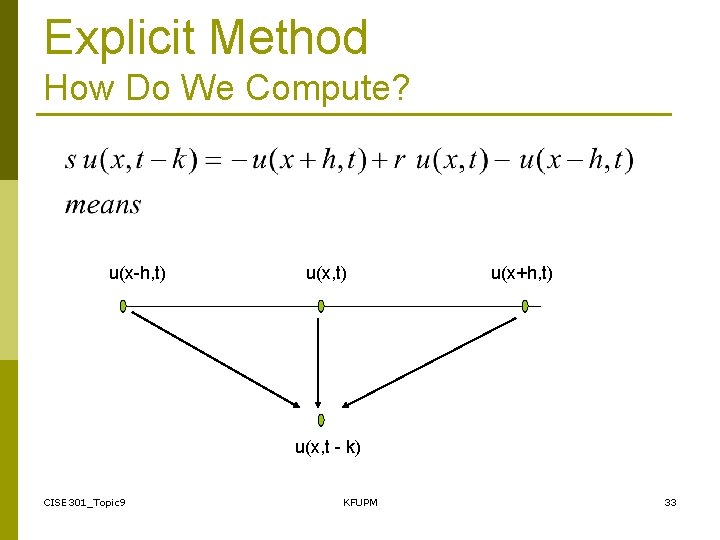
Explicit Method How Do We Compute? u(x-h, t) u(x+h, t) u(x, t - k) CISE 301_Topic 9 KFUPM 33

Crank-Nicolson Method CISE 301_Topic 9 KFUPM 34

Crank-Nicolson Method CISE 301_Topic 9 KFUPM 35

Examples p Explicit method to solve Parabolic PDEs. p Cranks-Nicholson Method. CISE 301_Topic 9 KFUPM 36

Heat Equation ice x CISE 301_Topic 9 KFUPM 37

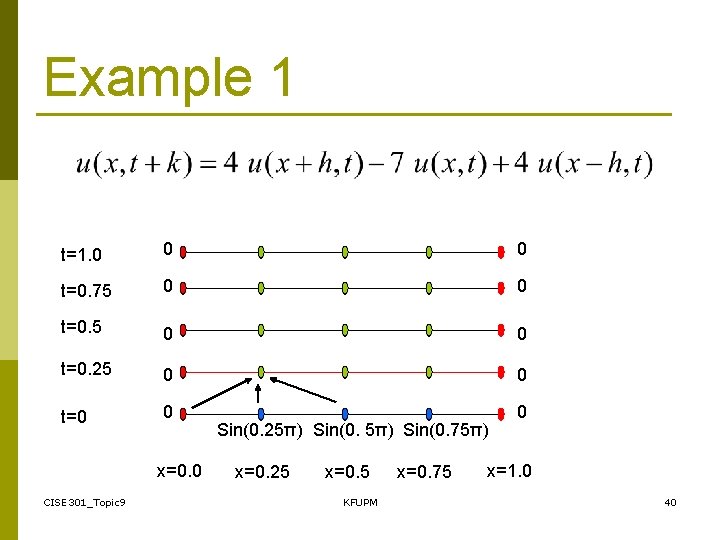
Example 1 CISE 301_Topic 9 KFUPM 38

Example 1 (Cont. ) CISE 301_Topic 9 KFUPM 39

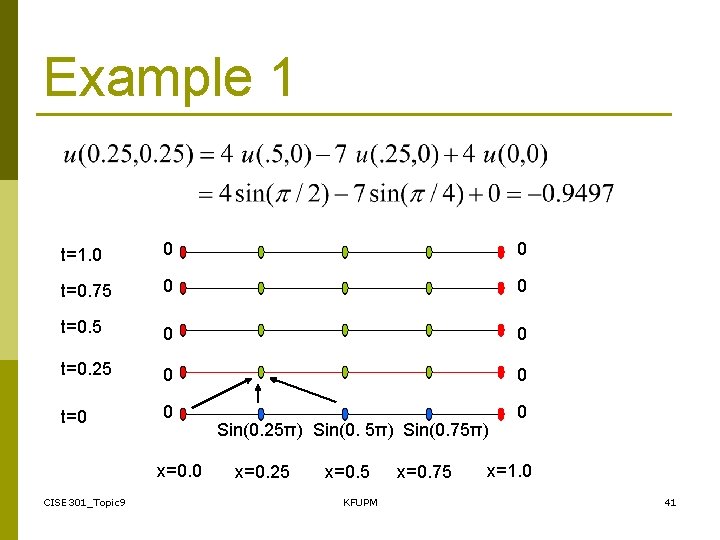
Example 1 t=1. 0 0 0 t=0. 75 0 0 t=0. 25 0 0 t=0 0 0 x=0. 0 CISE 301_Topic 9 Sin(0. 25π) Sin(0. 75π) x=0. 25 x=0. 5 KFUPM x=0. 75 x=1. 0 40

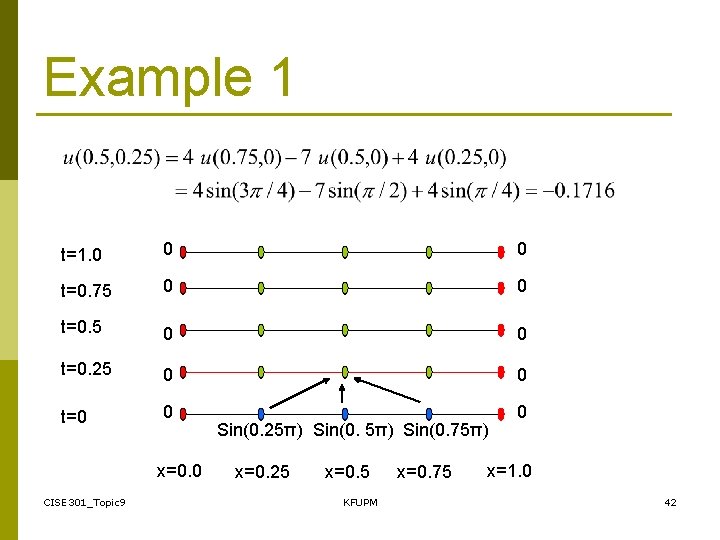
Example 1 t=1. 0 0 0 t=0. 75 0 0 t=0. 25 0 0 t=0 0 0 x=0. 0 CISE 301_Topic 9 Sin(0. 25π) Sin(0. 75π) x=0. 25 x=0. 5 KFUPM x=0. 75 x=1. 0 41

Example 1 t=1. 0 0 0 t=0. 75 0 0 t=0. 25 0 0 t=0 0 0 x=0. 0 CISE 301_Topic 9 Sin(0. 25π) Sin(0. 75π) x=0. 25 x=0. 5 KFUPM x=0. 75 x=1. 0 42

Remarks on Example 1 CISE 301_Topic 9 KFUPM 43

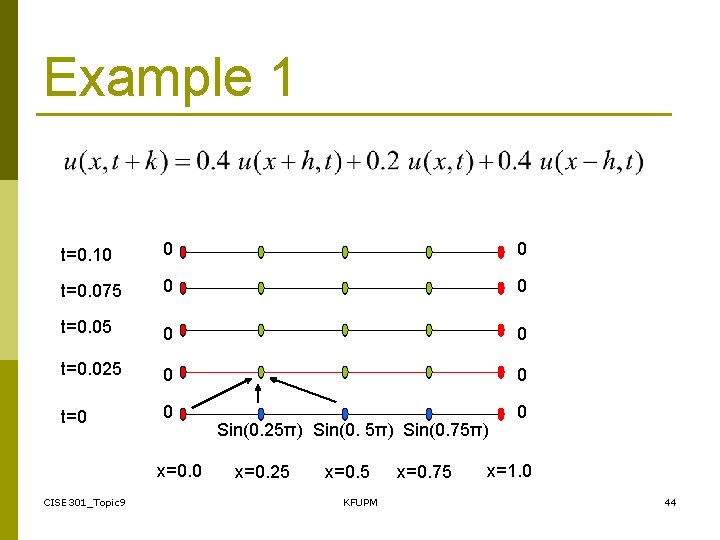
Example 1 t=0. 10 0 0 t=0. 075 0 0 t=0. 025 0 0 t=0 0 0 x=0. 0 CISE 301_Topic 9 Sin(0. 25π) Sin(0. 75π) x=0. 25 x=0. 5 KFUPM x=0. 75 x=1. 0 44

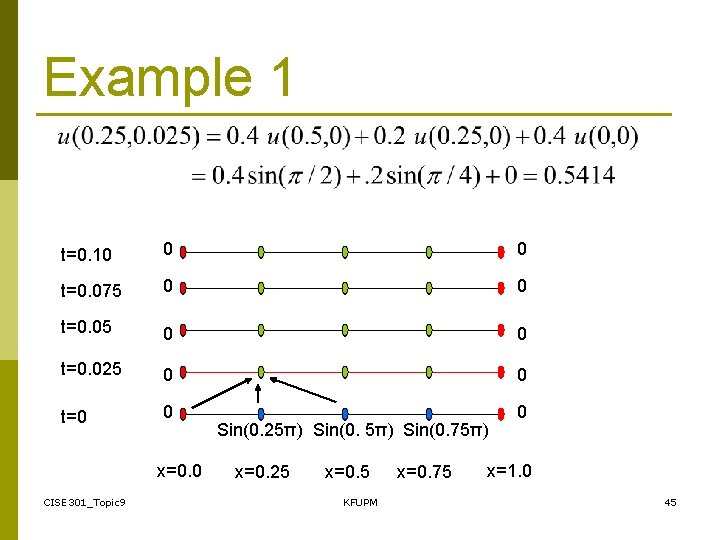
Example 1 t=0. 10 0 0 t=0. 075 0 0 t=0. 025 0 0 t=0 0 0 x=0. 0 CISE 301_Topic 9 Sin(0. 25π) Sin(0. 75π) x=0. 25 x=0. 5 KFUPM x=0. 75 x=1. 0 45

Example 1 t=0. 10 0 0 t=0. 075 0 0 t=0. 025 0 0 t=0 0 0 x=0. 0 CISE 301_Topic 9 Sin(0. 25π) Sin(0. 75π) x=0. 25 x=0. 5 KFUPM x=0. 75 x=1. 0 46

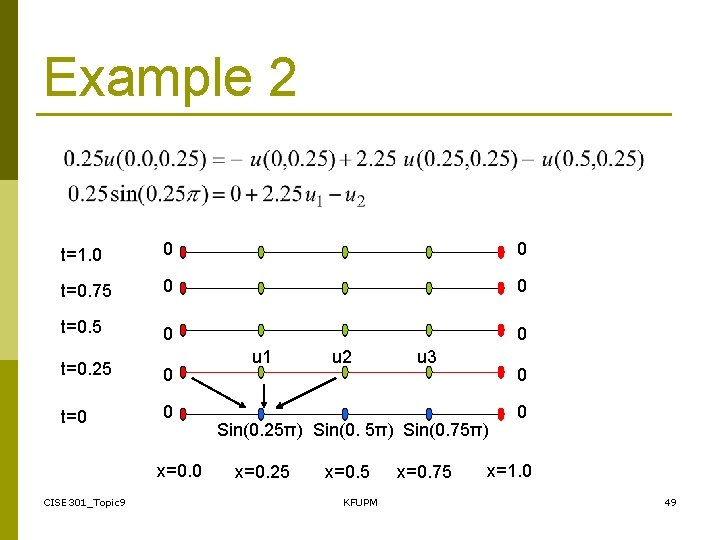
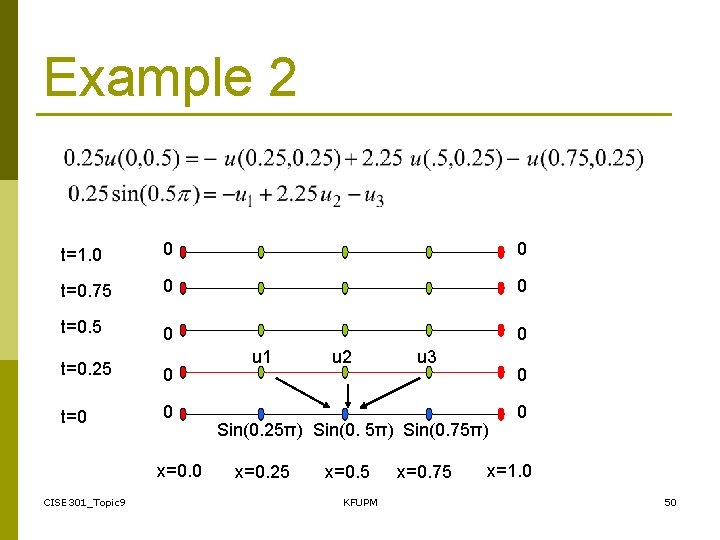
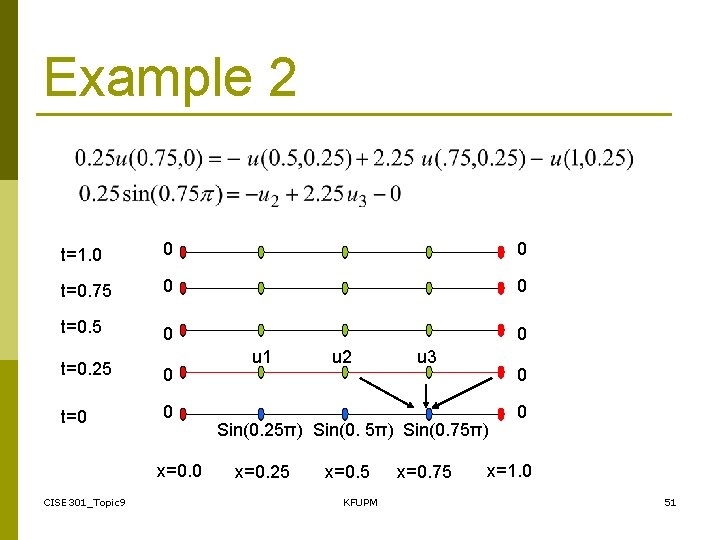
Example 2 CISE 301_Topic 9 KFUPM 47

Example 2 Crank-Nicolson Method CISE 301_Topic 9 KFUPM 48

Example 2 t=1. 0 0 0 t=0. 75 0 0 t=0. 25 0 t=0 0 x=0. 0 CISE 301_Topic 9 u 1 u 2 u 3 0 Sin(0. 25π) Sin(0. 75π) x=0. 25 x=0. 5 KFUPM x=0. 75 0 x=1. 0 49

Example 2 t=1. 0 0 0 t=0. 75 0 0 t=0. 25 0 t=0 0 x=0. 0 CISE 301_Topic 9 u 1 u 2 u 3 0 Sin(0. 25π) Sin(0. 75π) x=0. 25 x=0. 5 KFUPM x=0. 75 0 x=1. 0 50

Example 2 t=1. 0 0 0 t=0. 75 0 0 t=0. 25 0 t=0 0 x=0. 0 CISE 301_Topic 9 u 1 u 2 u 3 0 Sin(0. 25π) Sin(0. 75π) x=0. 25 x=0. 5 KFUPM x=0. 75 0 x=1. 0 51

Example 2 Crank-Nicolson Method CISE 301_Topic 9 KFUPM 52

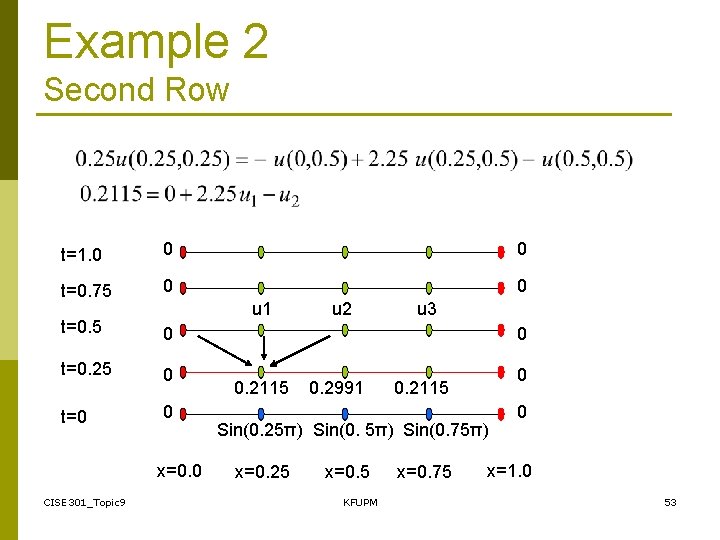
Example 2 Second Row t=1. 0 0 0 t=0. 75 0 0 t=0. 5 0 t=0. 25 0 t=0 0 u 1 x=0. 0 CISE 301_Topic 9 u 2 u 3 0 0. 2115 0. 2991 0 0. 2115 Sin(0. 25π) Sin(0. 75π) x=0. 25 x=0. 5 KFUPM x=0. 75 0 x=1. 0 53

Example 2 The process is continued until the values of u(x, t) on the desired grid are computed. CISE 301_Topic 9 KFUPM 54

Remarks The Explicit Method: • One needs to select small k to ensure stability. • Computation per point is very simple but many points are needed. Cranks Nicolson: • Requires the solution of a Tridiagonal system. • Stable (Larger k can be used). CISE 301_Topic 9 KFUPM 55

Lecture 39 Elliptic Equations p p p CISE 301_Topic 9 Elliptic Equations Laplace Equation Solution KFUPM 56

Elliptic Equations CISE 301_Topic 9 KFUPM 57

Laplace Equation Laplace equation appears in several engineering problems such as: n n Studying the steady state distribution of heat in a body. Studying the steady state distribution of electrical charge in a body. CISE 301_Topic 9 KFUPM 58

Laplace Equation p Temperature is a function of the position (x and y) p When no heat source is available f(x, y)=0 CISE 301_Topic 9 KFUPM 59

Solution Technique A grid is used to divide the region of interest. p Since the PDE is satisfied at each point in the area, it must be satisfied at each point of the grid. p A finite difference approximation is obtained at each grid point. p CISE 301_Topic 9 KFUPM 60

Solution Technique CISE 301_Topic 9 KFUPM 61

Solution Technique CISE 301_Topic 9 KFUPM 62

Solution Technique CISE 301_Topic 9 KFUPM 63

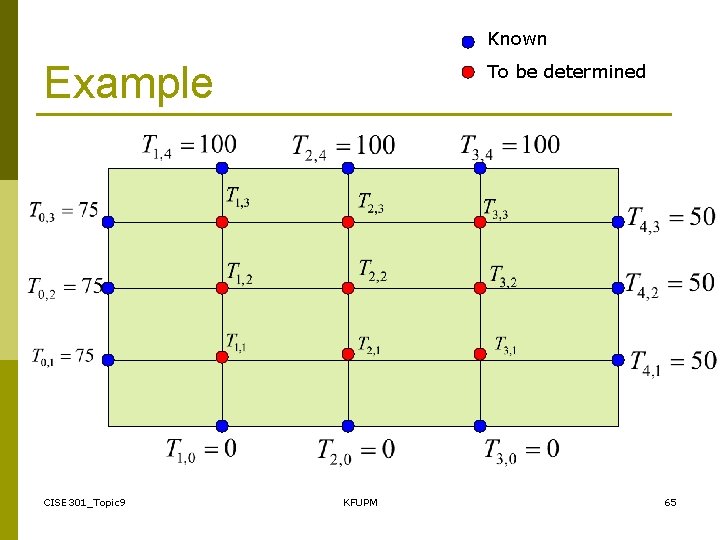
Example It is required to determine the steady state temperature at all points of a heated sheet of metal. The edges of the sheet are kept at a constant temperature: 100, 50, 0, and 75 degrees. 100 75 50 The sheet is divided to 5 X 5 grids. CISE 301_Topic 9 0 KFUPM 64

Known Example CISE 301_Topic 9 To be determined KFUPM 65

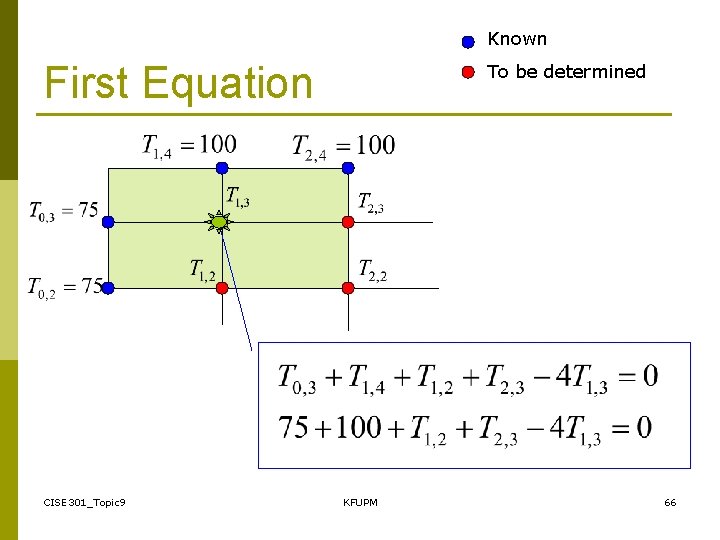
Known First Equation CISE 301_Topic 9 To be determined KFUPM 66

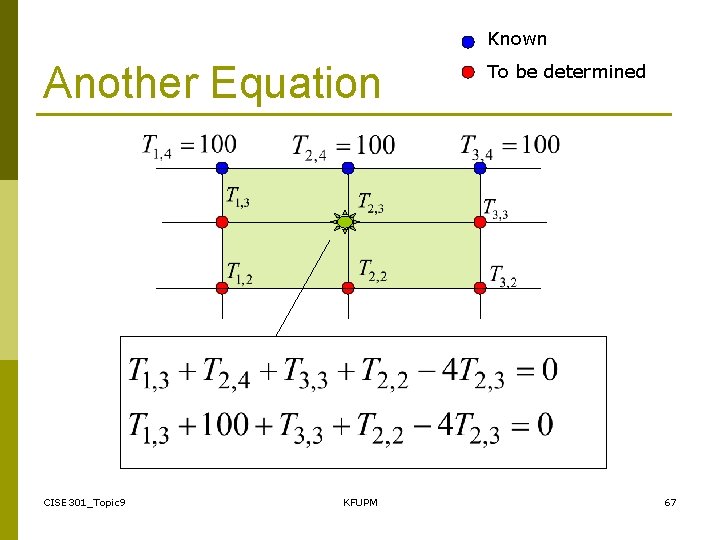
Known Another Equation CISE 301_Topic 9 KFUPM To be determined 67

Solution The Rest of the Equations CISE 301_Topic 9 KFUPM 68

Convergence and Stability of the Solution p Convergence The solutions converge means that the solution obtained using the finite difference method approaches the true solution as the steps approach zero. p Stability: An algorithm is stable if the errors at each stage of the computation are not magnified as the computation progresses. CISE 301_Topic 9 KFUPM 69