Patterson Space and Heavy Atom Isomorphous Replacement MIR

Patterson Space and Heavy Atom Isomorphous Replacement MIR = Multiple heavy atom Isomorphous Replacement phasing SIR = Single heavy atom Isomorphous Replacement phasing

Amplitudes for a 2 atom crystal The amplitude of a wave F(h k l) scattered by just 2 atoms depends on the distance between them in the (h k l) direction. Ignoring phase, what happens to the amplitude as the two atoms slide perpendicular to the Bragg planes? It stays the same. Only the phase changes.

Largest amplitudes are when atoms are in-phase If two atoms are in-phase, they have the largest amplitude. If one of the atoms (either one) is at the origin, then the phase is 0°

Phase zero Fourier transform Whatever the true phases of the F’s, if they are set to zero, then the density goes to the points of intecsection, which are the interatom vectors. The phase zero inverse Fourier is called a Patterson Map

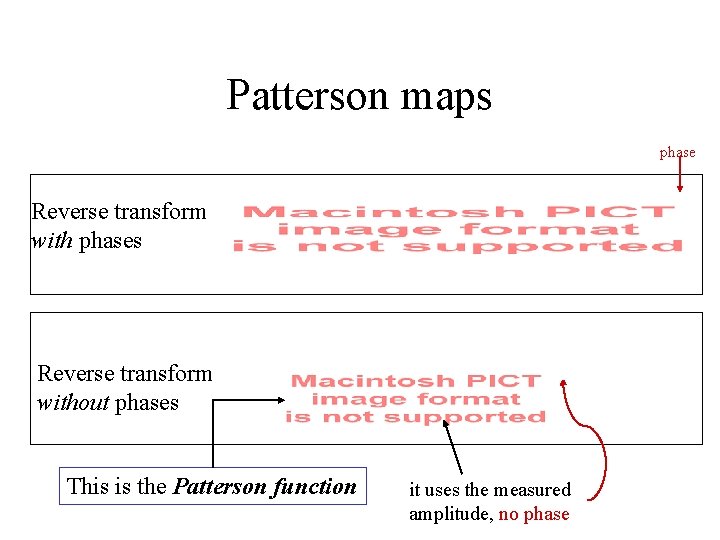
Patterson maps phase Reverse transform with phases Reverse transform without phases This is the Patterson function it uses the measured amplitude, no phase

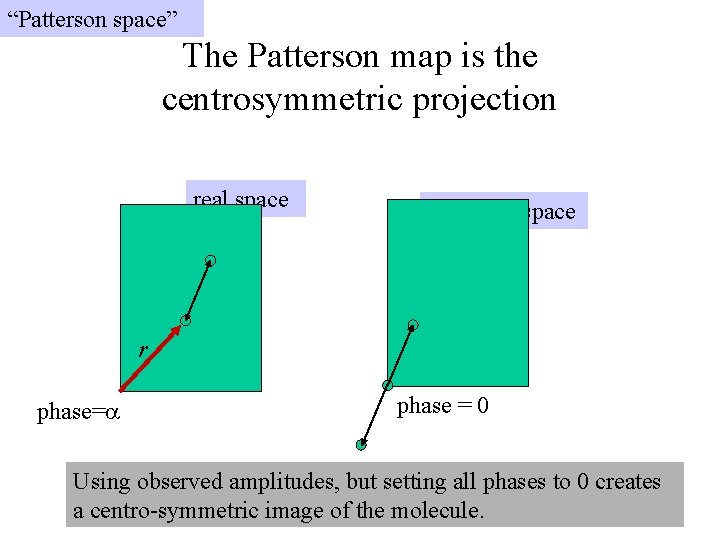
“Patterson space” The Patterson map is the centrosymmetric projection real space Patterson space r phase=a phase = 0 Using observed amplitudes, but setting all phases to 0 creates a centro-symmetric image of the molecule.

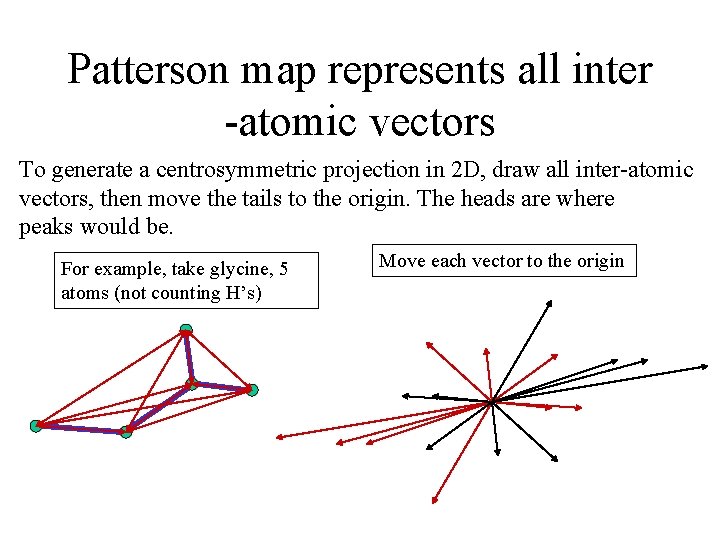
Patterson map represents all inter -atomic vectors To generate a centrosymmetric projection in 2 D, draw all inter-atomic vectors, then move the tails to the origin. The heads are where peaks would be. For example, take glycine, 5 atoms (not counting H’s) Move each vector to the origin

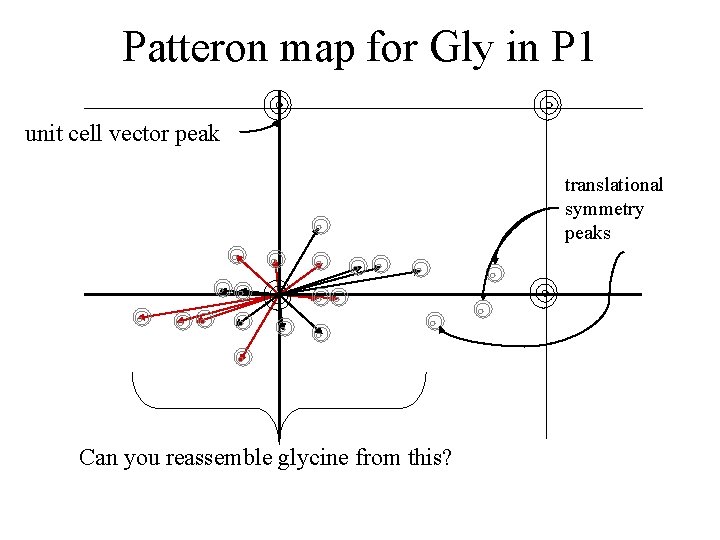
Patteron map for Gly in P 1 unit cell vector peak translational symmetry peaks Can you reassemble glycine from this?

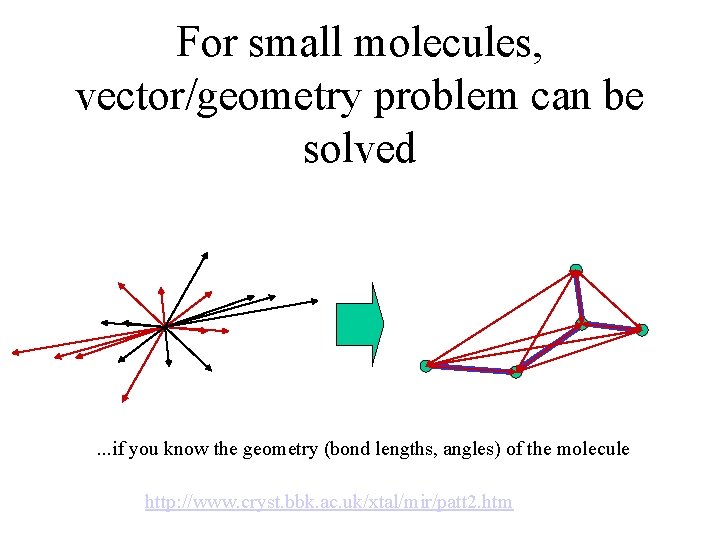
For small molecules, vector/geometry problem can be solved . . . if you know the geometry (bond lengths, angles) of the molecule http: //www. cryst. bbk. ac. uk/xtal/mir/patt 2. htm

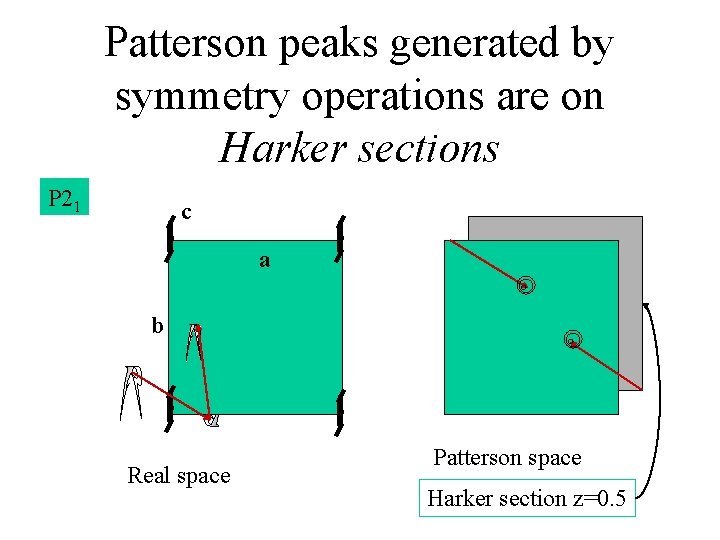
Patterson peaks generated by symmetry operations are on Harker sections P 21 c a b Real space Patterson space Harker section z=0. 5

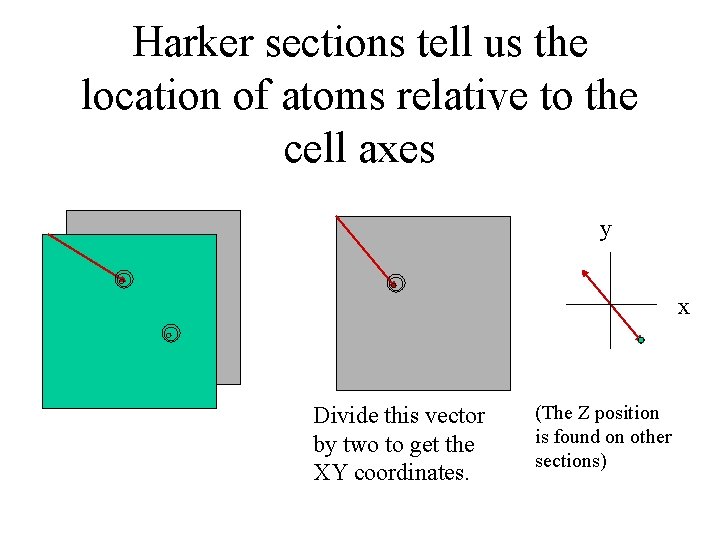
Harker sections tell us the location of atoms relative to the cell axes y x Divide this vector by two to get the XY coordinates. (The Z position is found on other sections)

Non-Harker sections tell us interatomic vectors not related by symmetry If there is more than one atom in the asu, you can get the vector between them by searching for peaks in non-Harker sections of the Patterson. (like the glycine example) Then, combining knowledge from Harker sections (giving absolute positions) and non-Harker sections (giving relative positions) we can get the atomic coordinates.

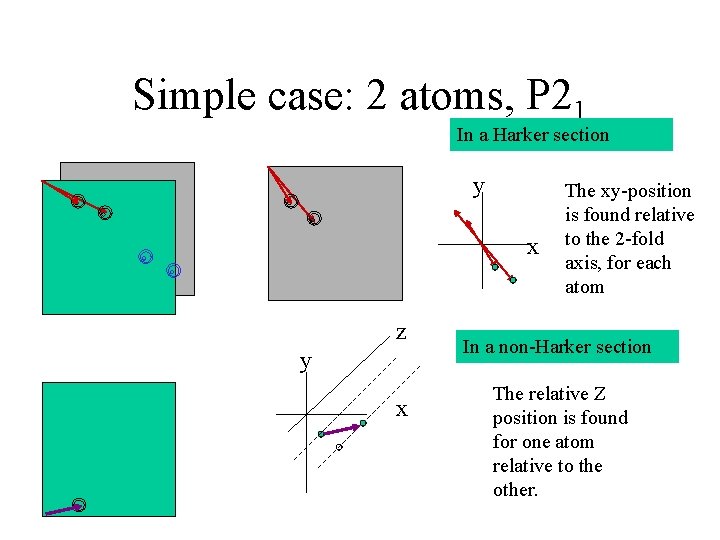
Simple case: 2 atoms, P 21 In a Harker section y x z y x The xy-position is found relative to the 2 -fold axis, for each atom In a non-Harker section The relative Z position is found for one atom relative to the other.

Protein Patterson maps are a mess Even if atomic resolution data is available, no individual atom-atom peaks can be identified because of overlap. The number of atom-atom peaks goes up as the square of the number of atoms.

In class exercise: make a Patterson map Using the Escher Web Sketch: Set the space group to P 4 mm Place one atom at (0. 4, 0. 25) Draw the Patterson vectors. Place a second atom (different color) at (0. 2, 0. 1) Draw the Patterson vectors.

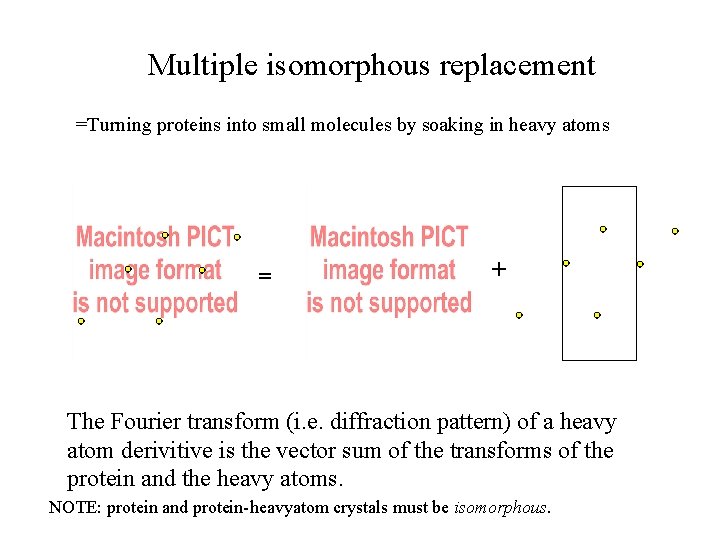
Multiple isomorphous replacement =Turning proteins into small molecules by soaking in heavy atoms = + The Fourier transform (i. e. diffraction pattern) of a heavy atom derivitive is the vector sum of the transforms of the protein and the heavy atoms. NOTE: protein and protein-heavyatom crystals must be isomorphous.

Subtracting amplitudes is like subtracting density, almost = – FH = FPH –FP FH, the Fourier transform of the heavy atoms is the vector difference of FPH and FH. |FH| ≈ |FPH| – |FP|

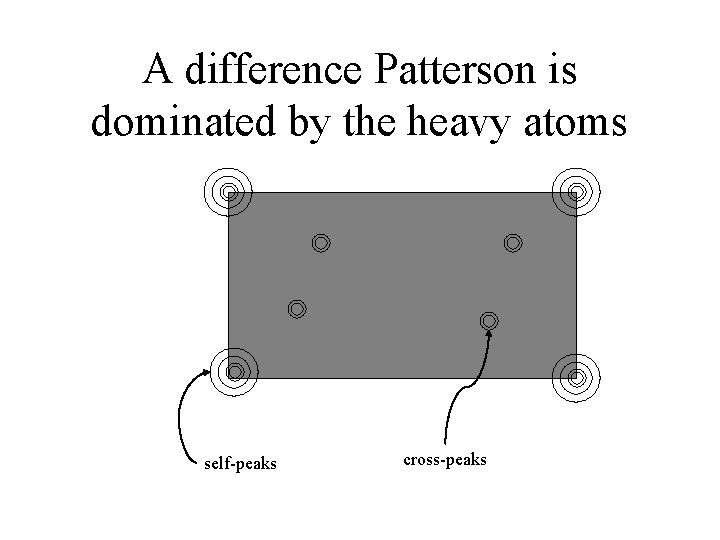
Subtracting Fourier transforms We can’t do FPH – FP = FH i directly because we don’t know the phases. Assume, for the moment, that |FH| << |FP| , |FPH|. Then the phases of FP and FPH are approximately the same. So, |FPH–FP| ≈ |FPH| – |FP| FP FH FPH In that case, the Patterson map based on |FPH|–|FP| will be approximately equal to Patterson map based on the true |FH|.

A difference Patterson is dominated by the heavy atoms self-peaks cross-peaks

In class exercise: solving a simple Patterson peak (0. 5, 0. 1, 0. 333) Space group is P 31 a Where are the 3 heavy atoms? (1) Draw a trigonal unit cell (2) Draw an equilateral triangle around the cell origin such that XY from these two vectors are the sides. b (3) Estimate the coordinates of the triangle vectices.

In class exercise: solving a Patterson peaks at (0. 4, 0. 2, 0. 333), (-0. 1, 0. 5, 0. 333), (0. 5, -0. 3, 333) Space group is P 31 Where are the 3 heavy atoms? (1) Draw a trigonal unit cell (2) Draw an equilateral triangle around the cell origin such that XY from these two vectors are the sides. (3) Estimate the coordinates of the triangle vectices.

Calculating FH from the heavy atom coordinates g=all heavy atoms Once we know the heavy atom coordinates, we can calculate amplitude and phase for all reflections FH.

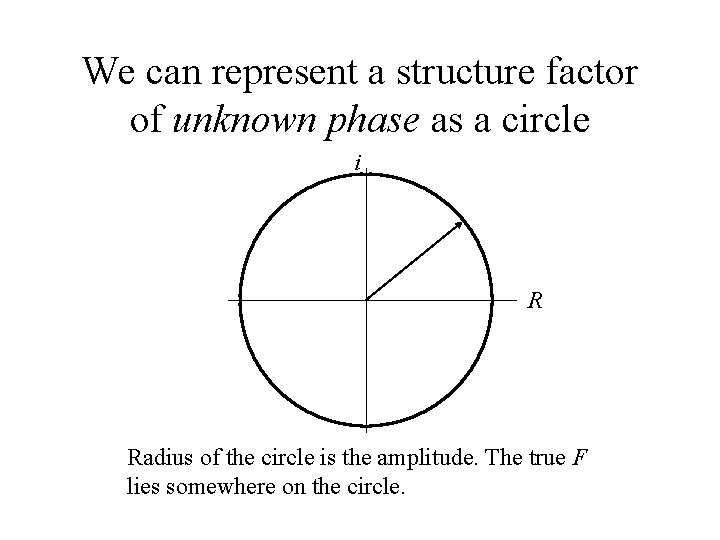
We can represent a structure factor of unknown phase as a circle i R Radius of the circle is the amplitude. The true F lies somewhere on the circle.

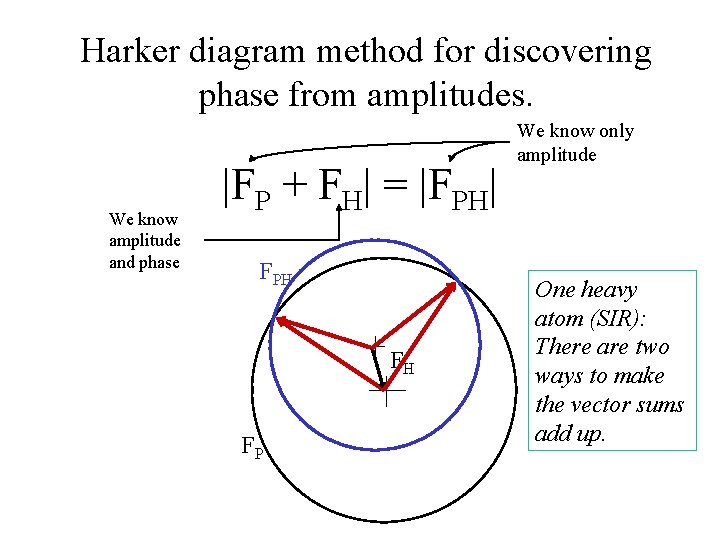
Harker diagram method for discovering phase from amplitudes. We know amplitude and phase |FP + FH| = |FPH| FPH FH FP We know only amplitude One heavy atom (SIR): There are two ways to make the vector sums add up.

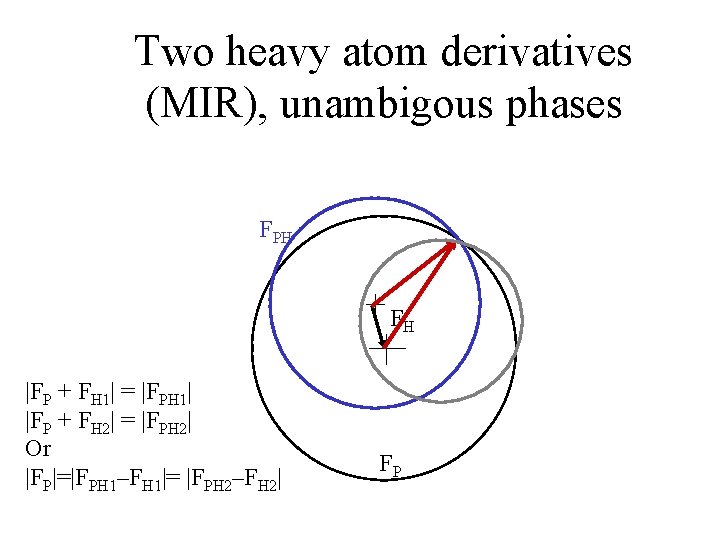
Two heavy atom derivatives (MIR), unambigous phases FPH FH |FP + FH 1| = |FPH 1| |FP + FH 2| = |FPH 2| Or |FP|=|FPH 1–FH 1|= |FPH 2–FH 2| FP

In class exercise: Solve the phase problem for one F using two FH’s |FP| = 29. 0 Draw three circles with the three diameters (scale doesn’t matter) |FPH 1| = 26. 0 Offset the PH 1 circle from the P circle by -FH 1 |FPH 2| = 32. 0 Offset the PH 2 circle from the P circle by -FH 2 FH 1 = 7. 8 a. H 1 =155° FH 2 = 11. 0 a. H 1 =9° Find the intersection of the circles

Additional topics Crystal packing, solvent content, Mathews number, reciprocal space symmetry, amplitude error and phase error.

Crystal packing Protein crystal packing interactions are salt-bridges and Hbonds mostly. These are much weaker than the hydrophobic interactions that hold proteins together. This means that (1) protein crystals are fragile, and (2) proteins in crystals are probably not significantly distorted from their native conformations.

Reminder: The asymmetric unit = the smallest region of the unit cell that is sufficient to generate the whole unit cell by symmetry. For space group P 1, the whole cell is the asymmetric unit. For other space groups, it is the fraction of the unit cell corresponding to 1/Z where Z = the number of equivalent positions. For P 212121 Z = 4 (x, y, z) (–x, –y+1/2, –z+1/2) (–x+1/2, y+1/2, –z)� (x+1/2, –y, z+1/2). So the asymmetric unit will be 1/4 of the unit cell. asu

How many molecules are in the asu? (1)First find the total volume of the unit cell, Vcell. (2)Divide by the number of equivalent positions, Z, this is the volume of the asymmetric unit (Vasu=Vcell/Z) (3)Calculate the approximate volume of your molecule using the molecular weight and the density of protein, about 1. 35 g/ml. Vmol = ((MW/(1. 35 g/ml))/Nav) • 1024Å3/ml (4)Assume the number of molecules in the asu is n. Calculate percent solvent in the crystal: Psol=100% • (Vasu-n Vmol)/ Vasu

Quicker and easier: Matthews’ number is VM= Vcell/MW • Z Molecular weight is roughly the number of residues in the sequence x 110. Z is the number of equivalent positions. Matthews’ number for proteins varies from 1. 66 to 4. 0 for crystals with 30% to 75% solvent. If VM is too high, there must be more molecules in the asu than you thought.

In class exercise: how many molecules are in the asymmetric unit? Your molecule has 62 residues. Your crystal cell dimensions are 40 x 50 x 60Å, orthorhombic. P 212121 (Z=4). Use Matthews’ number to get n. VM= Vcell/(n. MW • Z) Get molecular volume. Vmol=((MW/(1. 35 g/ml))/Nav) • 1024Å3/ml ≈ 1. 23 MW Percent solvent? Psol=100% • (Vasu-n Vmol)/ Vasu

answer Molecular weight is roughly 62*110 = 6820 g/mol Vmol = 1. 23 * 6820 = 8390Å3 Vasu = (40*50*60)/4 = 30000Å3 if n=1, VM = 120000/(4* 6820) = 4. 39 too high!! if n=2, VM = 120000/(4* 2*6820) = 2. 2 =just right so n=2 Percent solvent = (30000 - 2*8390)/30000 = 44%

The Phase Problem Oh no. We can’t measure phases! X-ray detectors (film, photomultiplier tubes, CCDs, etc) can measure only the intensity of the X-rays (which is the amplitude squared), but we need the full wave equations Aeia for each reflection to do the reverse Fourier transform. And because it is called the phase “problem”, the process of getting the phases is called a “solution”. That’s why we say we “solved” the crystal structure, instead of “measured” or “determined” it.

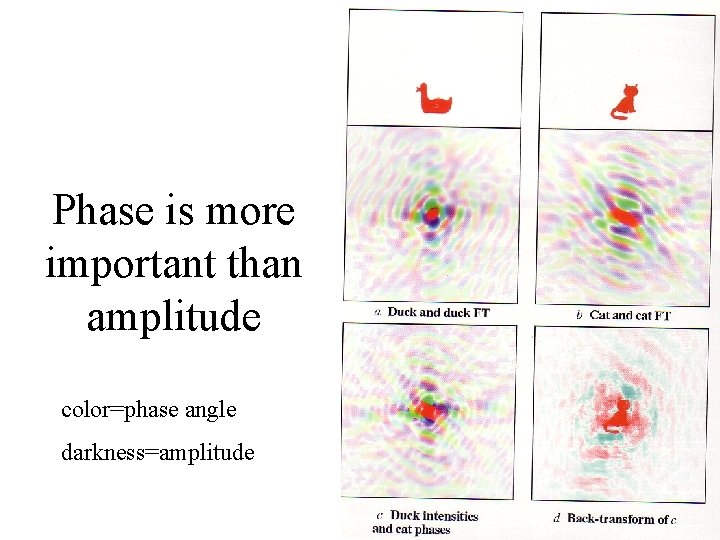
Phase is more important than amplitude color=phase angle darkness=amplitude

Reciprocal space symmetry Rotating the crystal rotates the reciprocal lattice by the same amount. Applying a mirror or inversion does the same to the reciprocal lattice. So the symmetry in the reciprocal lattice is the same as the symmetry in the crystal, with the addition of Friedel symmetry, but without translational symmetry. The addition of Friedel symmetry causes mirror planes to appear in reciprocal space when there is 2 -fold rotational symmetry in the crystal. (h, k, l) ===> (-h, -k, l) ===> (h, k, -l) 2 -fold Friedel mirror (h, k, -l)

Reciprocal space symmetry operators are the transpose. . . of the real space symmetry operators. The forward transform is summed over all atoms in the asu, and all symmetry operators Z. So the reverse transform is summed over the unique set, times Z.

Transposing the matrix is the same as reversing the order of multiplication Flip the matrix and change the order, and you get the same thing (written as a column instead of a row)

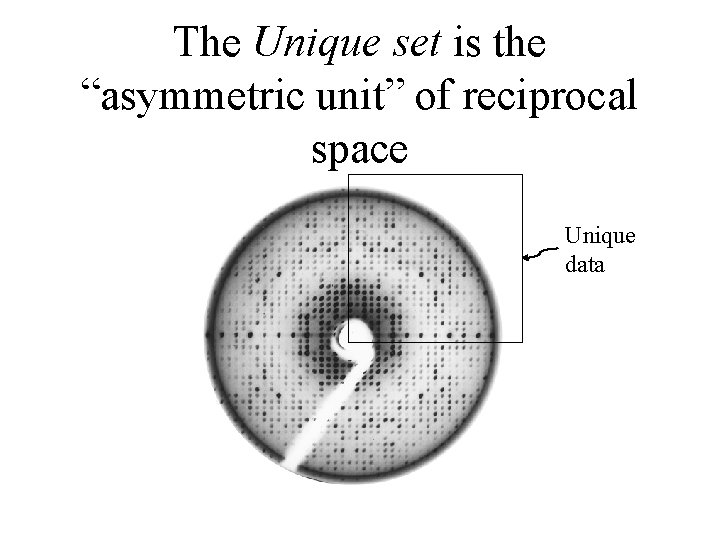
The Unique set is the “asymmetric unit” of reciprocal space Unique data

Initial phases Phases are not measured exactly because amplitudes are not measured exactly. Error bars on FP and FPH create a distribution of possible phase values a. width of circle is 1 s deviation, derived from data collection statistics.