Patrulatere nscrise n cerc Poligoane regulate Definiii Aplicaii

Patrulatere înscrise în cerc Poligoane regulate §Definiţii §Aplicaţii §Construcţii §Formule Şcoala cu clasele I-VIII Petőfi Sándor, Tg. Secuiesc Prof. Istók Éva

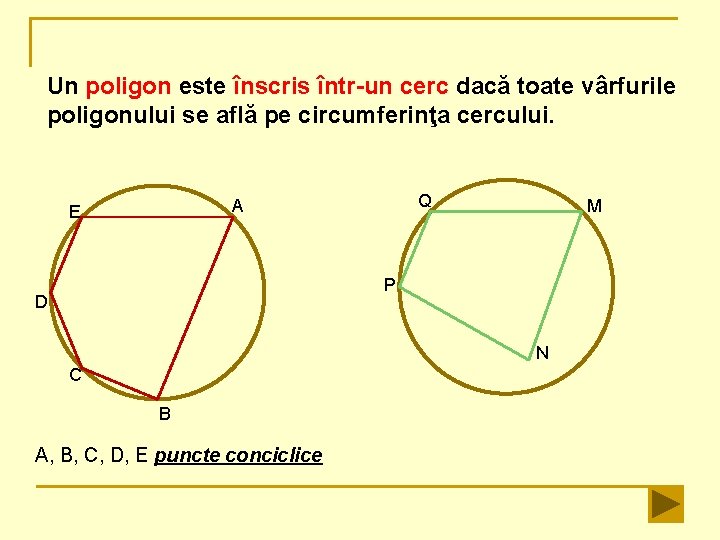
Un poligon este înscris într-un cerc dacă toate vârfurile poligonului se află pe circumferinţa cercului. Q A E M P D N C B A, B, C, D, E puncte conciclice

Un poligon se numeşte inscriptibil într-un cerc, dacă există un cerc care trece prin fiecare vârf al său. Orice triunghi este inscriptibil, centrul cercului circumscris fiind punctul de intersecţie al mediatoarelor. Nu orice patrulater este inscriptibil ! Teoreme

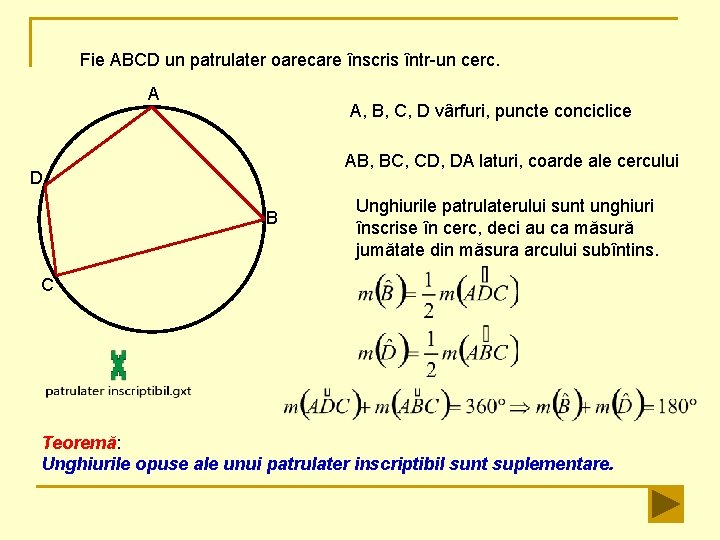
Fie ABCD un patrulater oarecare înscris într-un cerc. A A, B, C, D vârfuri, puncte conciclice AB, BC, CD, DA laturi, coarde ale cercului D B Unghiurile patrulaterului sunt unghiuri înscrise în cerc, deci au ca măsură jumătate din măsura arcului subîntins. C Teoremă: Unghiurile opuse ale unui patrulater inscriptibil sunt suplementare.

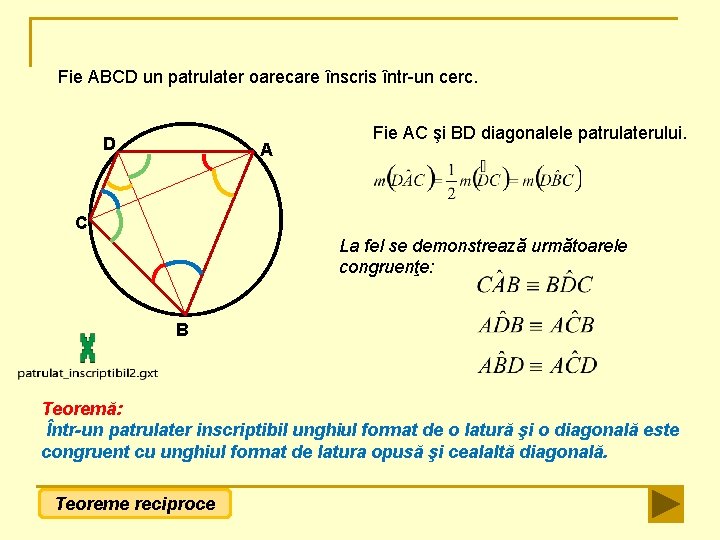
Fie ABCD un patrulater oarecare înscris într-un cerc. D A Fie AC şi BD diagonalele patrulaterului. C La fel se demonstrează următoarele congruenţe: B Teoremă: Într-un patrulater inscriptibil unghiul format de o latură şi o diagonală este congruent cu unghiul format de latura opusă şi cealaltă diagonală. Teoreme reciproce

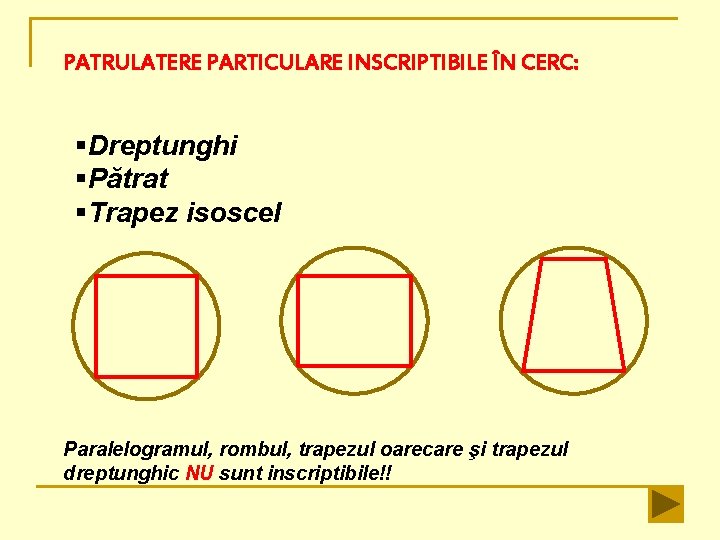
PATRULATERE PARTICULARE INSCRIPTIBILE ÎN CERC: §Dreptunghi §Pătrat §Trapez isoscel Paralelogramul, rombul, trapezul oarecare şi trapezul dreptunghic NU sunt inscriptibile!!

• Definiţii • Aplicaţii • Construcţii • Formule

Poligonul cu toate laturile şi toate unghiurile congruente se numeşte poligon regulat. !!Dreptunghiul şi rombul NU sunt poligoane regulate!! §Triunghi regulat = triunghi echilateral §Patrulater regulat = pătrat §Poligon regulat cu şase laturi = hexagon regulat Centrul poligonului regulat coincide cu centrul cercului circumscris/înscris §Triunghi echilateral: intersecţia mediatoarelor §Pătrat şi hexagon regulat: intersecţia diagonalelor

Distanţa de la centrul cercului de la laturile poligonului regulat se numeşte apotema poligonului. Într-un poligon regulat cu „n” laturi avem relaţiile: Măsura unghiurilor: Perimetrul: Aria:

Aplicaţii: 1. Utilizând formula precedentă determinaţi măsurile unghiurilor unui triunghi echilateral, al unui hexagon regulat şi al pentagonului regulat. (pentagon = poligon cu cinci laturi) 2. Ştiind că un pligon regulat are unghiurile de măsură 150°, determinaţi numărul laturilor. 3. Determinaţi măsurile unghiurilor la centru ce se formează la unirea centrului unui cerc cu vârfurile poligonului regulat cu opt laturi înscris în cerc! Cum se poate utiliza rezultatul găsit în construcţia acestui poligon?

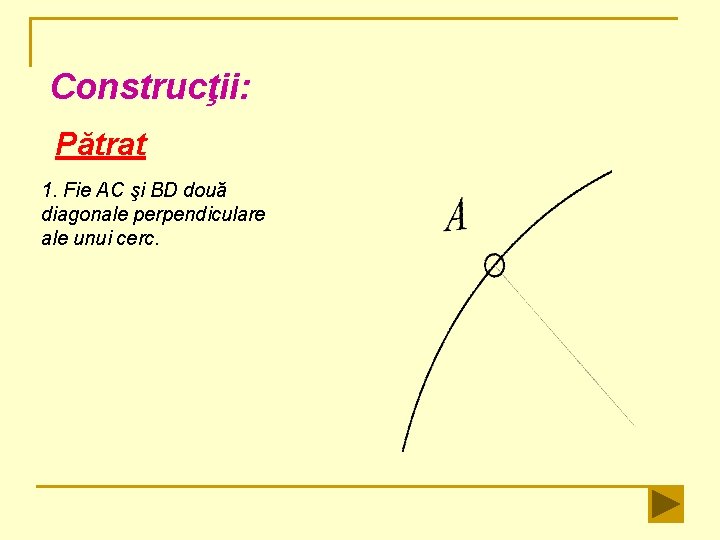
Construcţii: Pătrat 1. Fie AC şi BD două diagonale perpendiculare ale unui cerc.

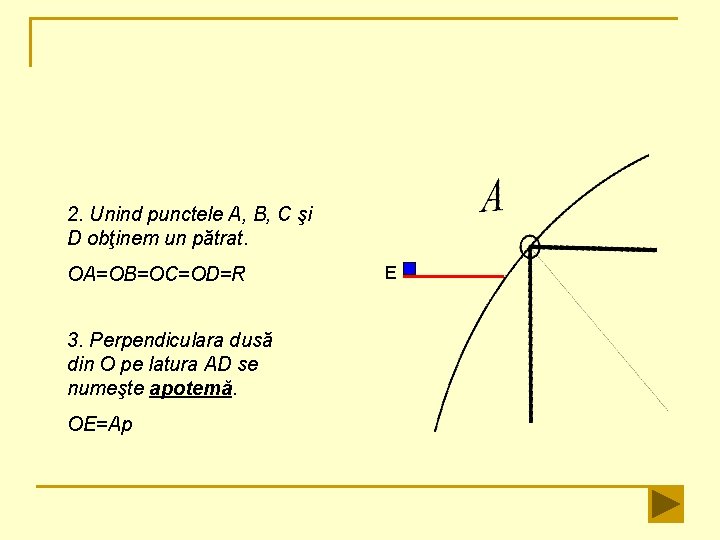
2. Unind punctele A, B, C şi D obţinem un pătrat. OA=OB=OC=OD=R 3. Perpendiculara dusă din O pe latura AD se numeşte apotemă. OE=Ap E

Hexagon regulat 1. Fie un cerc de rază R şi centru O. Cu ajutorul compasului cercul se împarte în şase arce congruente. R

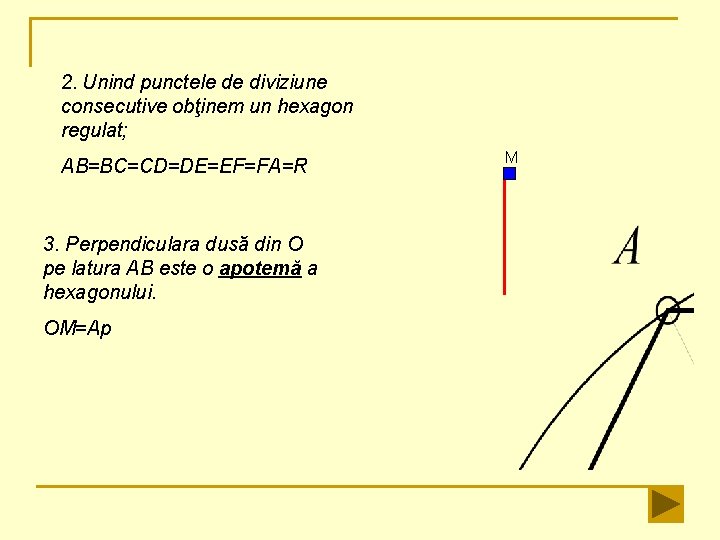
2. Unind punctele de diviziune consecutive obţinem un hexagon regulat; AB=BC=CD=DE=EF=FA=R 3. Perpendiculara dusă din O pe latura AB este o apotemă a hexagonului. OM=Ap M

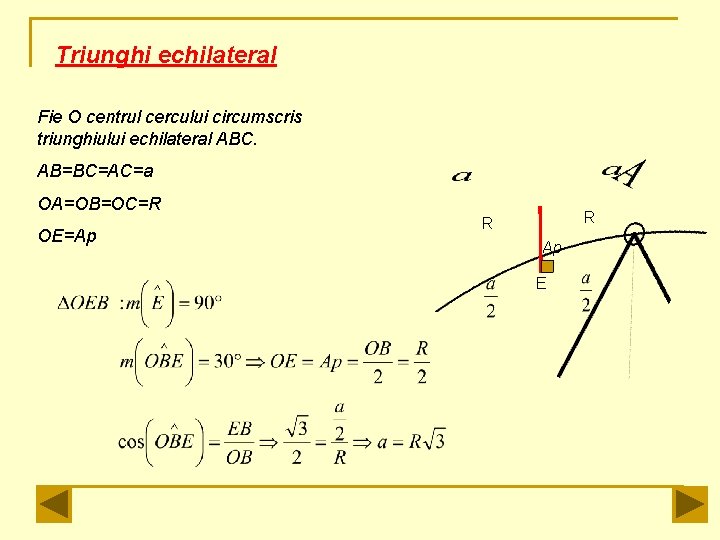
Triunghi echilateral 1. Costrucţia este identică cu cea a hexagonului, dar nu se vor uni punctele de diviziune consecutive. 2. Perpendiculara dusă din O pe latura AB este o apotemă a triunghiului. OE=Ap OA=OB=OC=R E

Triunghi echilateral Fie O centrul cercului circumscris triunghiului echilateral ABC. AB=BC=AC=a OA=OB=OC=R OE=Ap R R Ap E

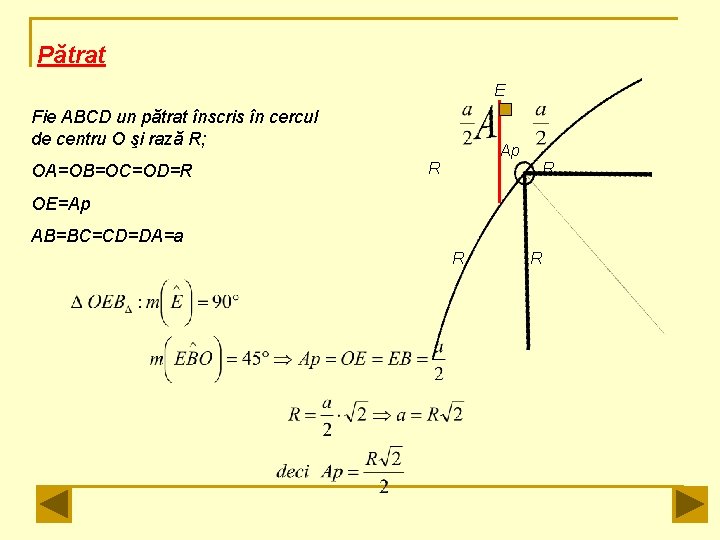
Pătrat E Fie ABCD un pătrat înscris în cercul de centru O şi rază R; OA=OB=OC=OD=R Ap R R OE=Ap AB=BC=CD=DA=a R R

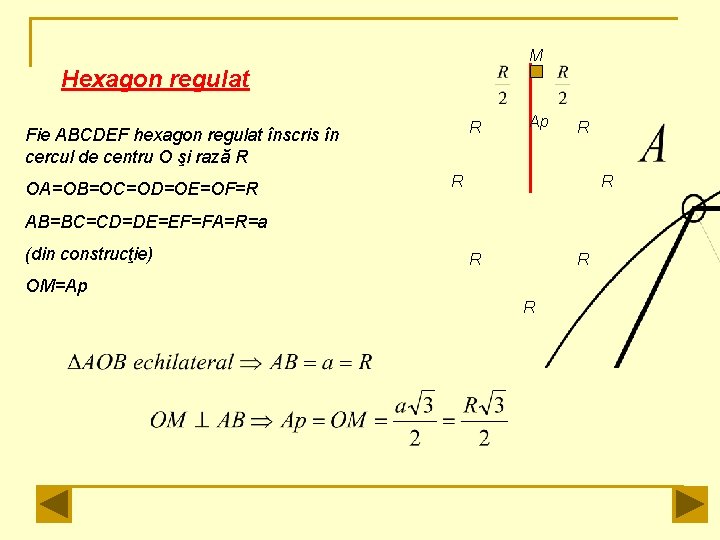
M Hexagon regulat R Fie ABCDEF hexagon regulat înscris în cercul de centru O şi rază R OA=OB=OC=OD=OE=OF=R Ap R R R AB=BC=CD=DE=EF=FA=R=a (din construcţie) R R OM=Ap R

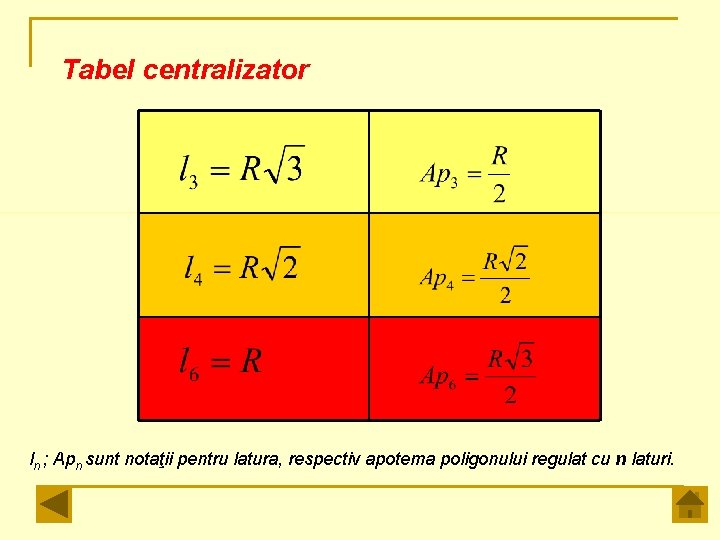
Tabel centralizator ln ; Apn sunt notaţii pentru latura, respectiv apotema poligonului regulat cu n laturi.