5 Poliedre platonice feele sunt poligoane regulate de

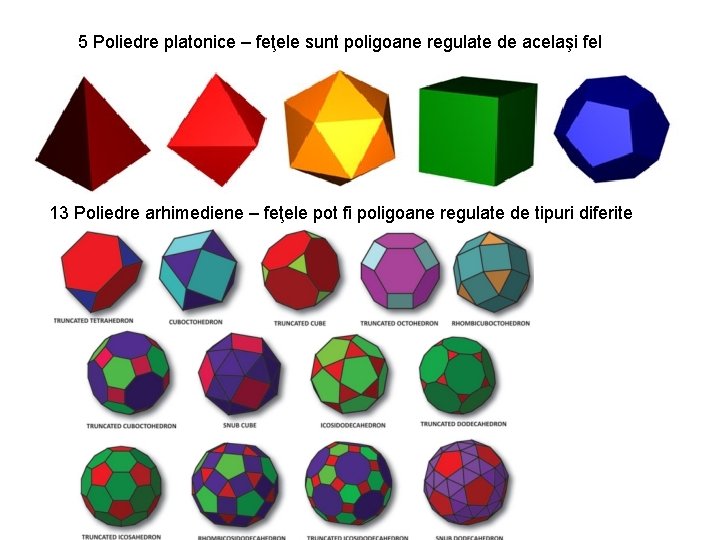
5 Poliedre platonice – feţele sunt poligoane regulate de acelaşi fel 13 Poliedre arhimediene – feţele pot fi poligoane regulate de tipuri diferite

Toate tipurile de grupuri finite de ordin ≤ 12: 1) (de ordin 1) grupul cu un element 2) (de ordin 2) grupul ciclic C 2 3) (de ordin 3) grupul ciclic C 3 4) (de ordin 4) grupul ciclic C 4 şi grupul lui Klein C 2 × C 2 5) (de ordin 5) grupul ciclic C 5 6) (de ordin 6) grupul ciclic C 6 şi grupul simetric S 3≈D 3≈A 3 7) (de ordin 7) grupul ciclic C 7 8) (de ordin 8) Grupul ciclic C 8, grupul C 4 × C 2, grupul C 2 × C 2 ≈D 2 x. C 2, grupul diedral D 4 şi grupul cuaternionilor H 8 ≈Q 2 9) (de ordin 9) grupul ciclic C 9 şi grupul C 3 × C 3 10) (de ordin 10) grupul ciclic C 10 şi grupul diedral D 5 11) (de ordin 11) grupul ciclic C 11 12) (de ordin 12) grupul ciclic C 12, grupul C 6 x. C 2≈C 3 x. D 2, grupul diedral D 6, grupul diciclic Q 3, grupul alternativ A 4. Singurele grupuri finite de simetrie (de rotaţie) posibile în trei dimensiuni sunt: Cn, Dn, A 4, S 4, A 5 Sau dacă se consideră şi inversiile (x -x) atunci: Cn x C 2, Dn x C 2, A 4 x C 2, S 4 x C 2, A 5 x C 2

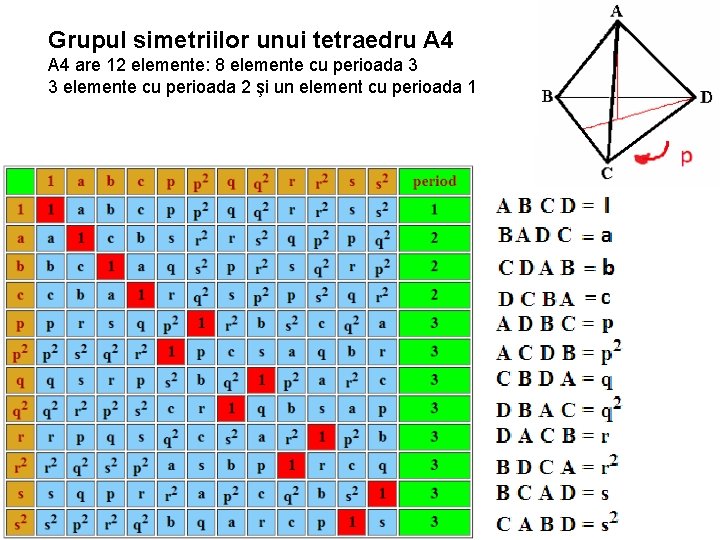
Grupul simetriilor unui tetraedru A 4 are 12 elemente: 8 elemente cu perioada 3 3 elemente cu perioada 2 şi un element cu perioada 1

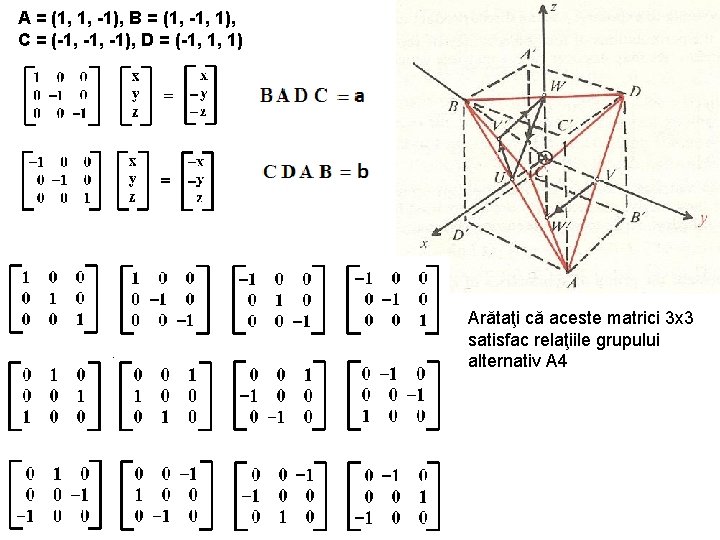
A = (1, 1, -1), B = (1, -1, 1), C = (-1, -1), D = (-1, 1, 1) Arătaţi că aceste matrici 3 x 3 satisfac relaţiile grupului alternativ A 4

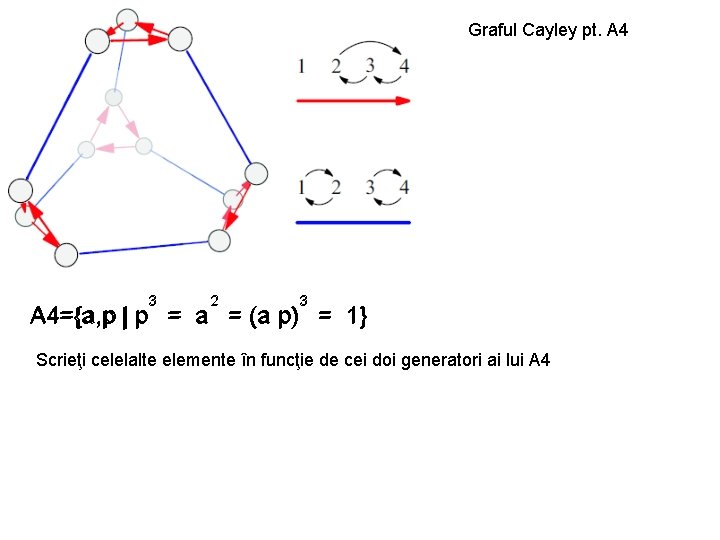
Graful Cayley pt. A 4 3 2 3 A 4={a, p | p = a = (a p) = 1} Scrieţi celelalte elemente în funcţie de cei doi generatori ai lui A 4

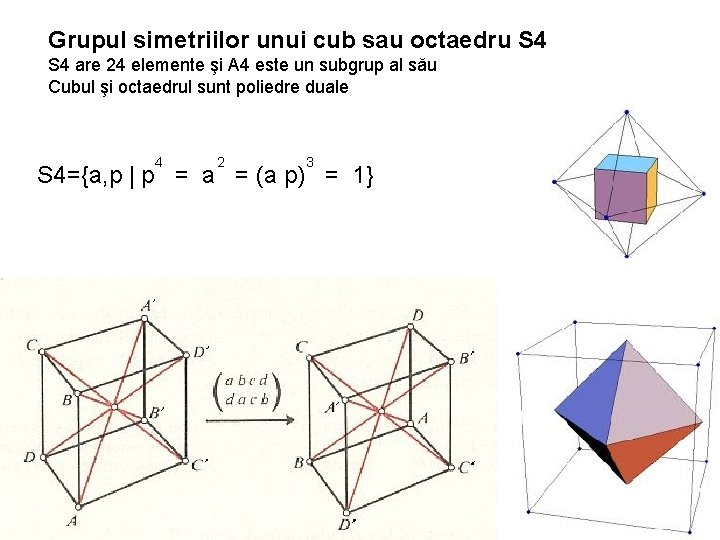
Grupul simetriilor unui cub sau octaedru S 4 are 24 elemente şi A 4 este un subgrup al său Cubul şi octaedrul sunt poliedre duale 4 2 3 S 4={a, p | p = a = (a p) = 1}

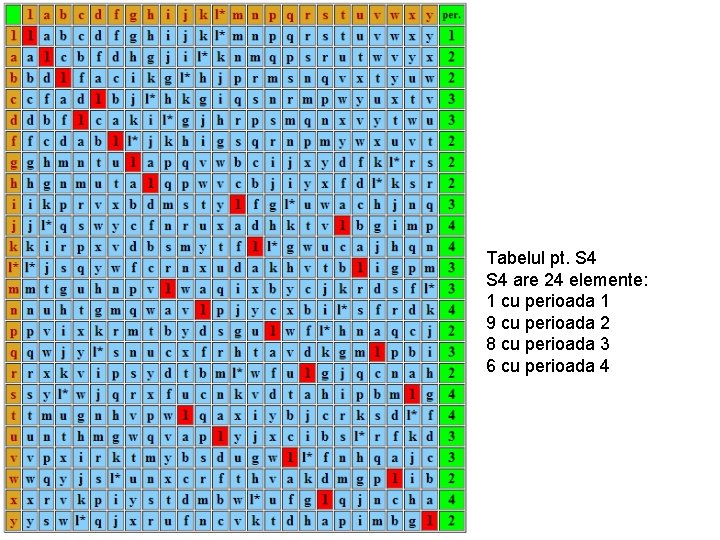
Tabelul pt. S 4 are 24 elemente: 1 cu perioada 1 9 cu perioada 2 8 cu perioada 3 6 cu perioada 4

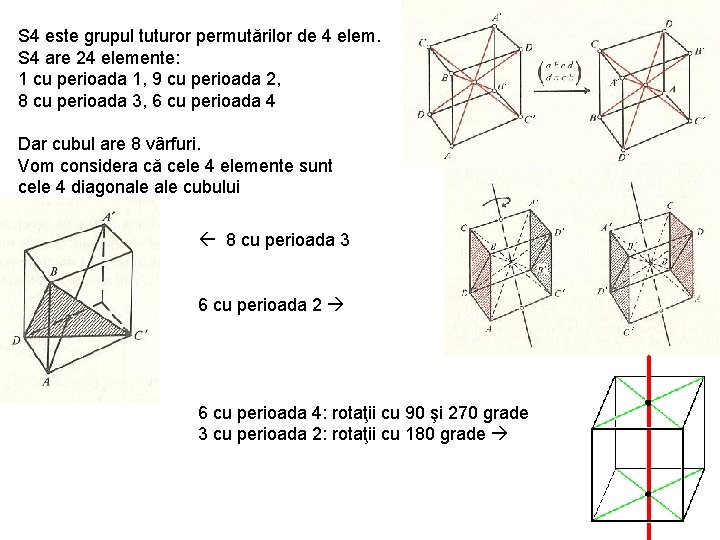
S 4 este grupul tuturor permutărilor de 4 elem. S 4 are 24 elemente: 1 cu perioada 1, 9 cu perioada 2, 8 cu perioada 3, 6 cu perioada 4 Dar cubul are 8 vârfuri. Vom considera că cele 4 elemente sunt cele 4 diagonale cubului 8 cu perioada 3 6 cu perioada 2 6 cu perioada 4: rotaţii cu 90 şi 270 grade 3 cu perioada 2: rotaţii cu 180 grade

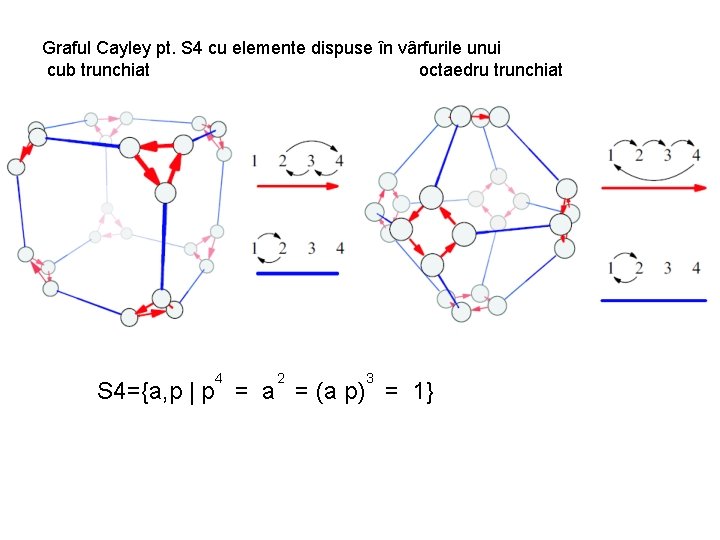
Graful Cayley pt. S 4 cu elemente dispuse în vârfurile unui cub trunchiat octaedru trunchiat 4 2 3 S 4={a, p | p = a = (a p) = 1}

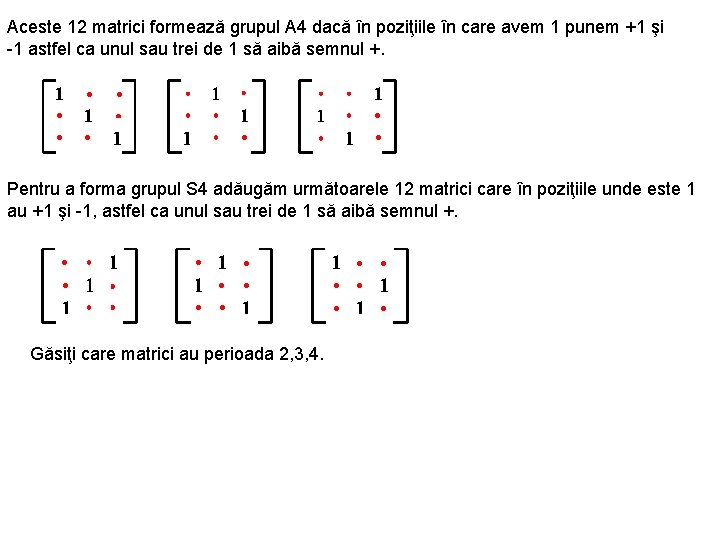
Aceste 12 matrici formează grupul A 4 dacă în poziţiile în care avem 1 punem +1 şi -1 astfel ca unul sau trei de 1 să aibă semnul +. Pentru a forma grupul S 4 adăugăm următoarele 12 matrici care în poziţiile unde este 1 au +1 şi -1, astfel ca unul sau trei de 1 să aibă semnul +. Găsiţi care matrici au perioada 2, 3, 4.

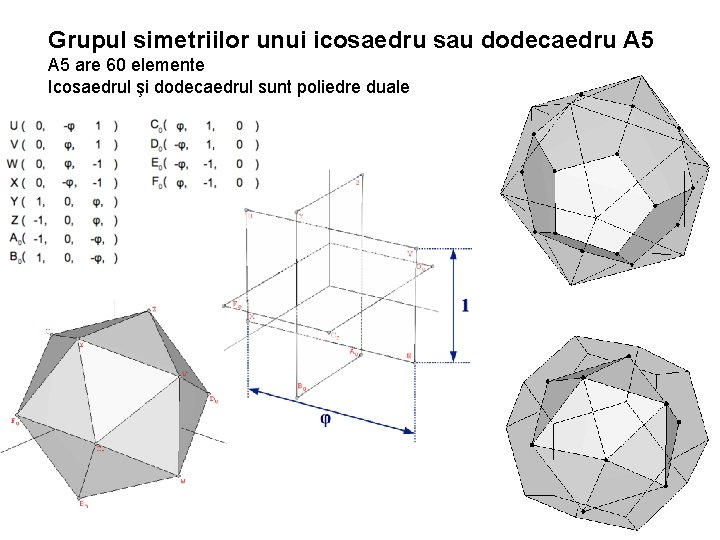
Grupul simetriilor unui icosaedru sau dodecaedru A 5 are 60 elemente Icosaedrul şi dodecaedrul sunt poliedre duale

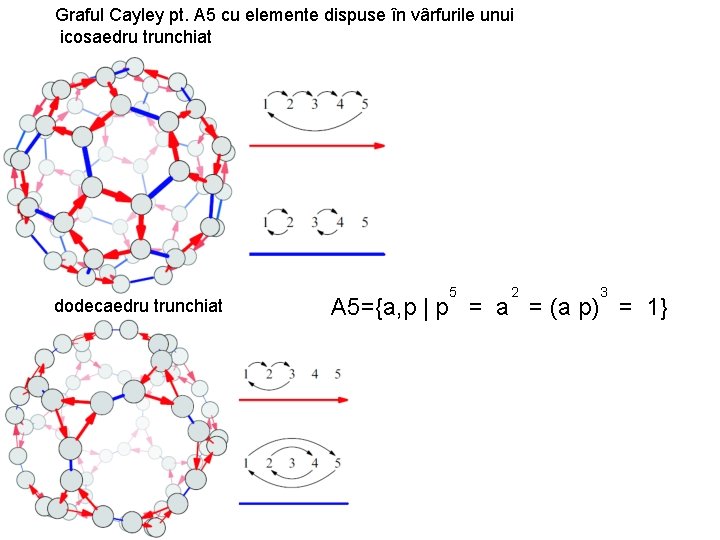
Graful Cayley pt. A 5 cu elemente dispuse în vârfurile unui icosaedru trunchiat dodecaedru trunchiat 5 2 3 A 5={a, p | p = a = (a p) = 1}

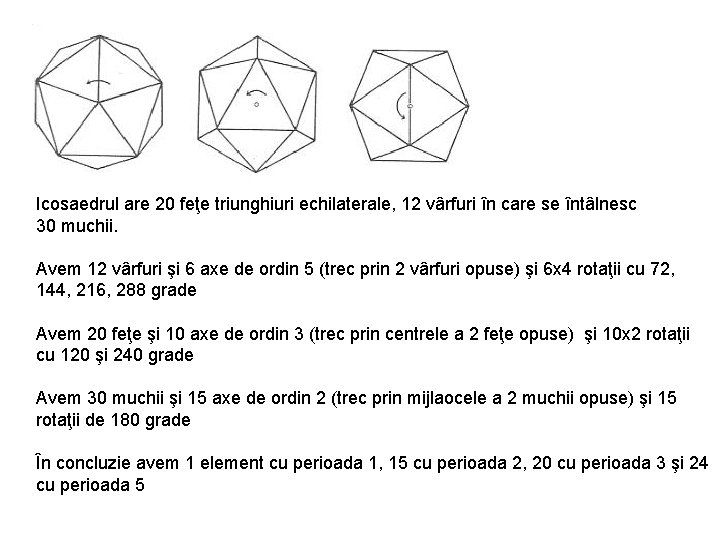
Icosaedrul are 20 feţe triunghiuri echilaterale, 12 vârfuri în care se întâlnesc 30 muchii. Avem 12 vârfuri şi 6 axe de ordin 5 (trec prin 2 vârfuri opuse) şi 6 x 4 rotaţii cu 72, 144, 216, 288 grade Avem 20 feţe şi 10 axe de ordin 3 (trec prin centrele a 2 feţe opuse) şi 10 x 2 rotaţii cu 120 şi 240 grade Avem 30 muchii şi 15 axe de ordin 2 (trec prin mijlaocele a 2 muchii opuse) şi 15 rotaţii de 180 grade În concluzie avem 1 element cu perioada 1, 15 cu perioada 2, 20 cu perioada 3 şi 24 cu perioada 5

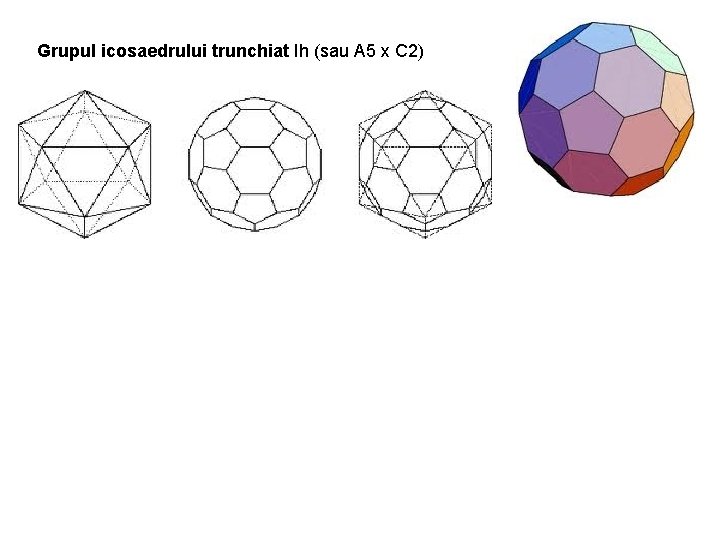
Grupul icosaedrului trunchiat Ih (sau A 5 x C 2)

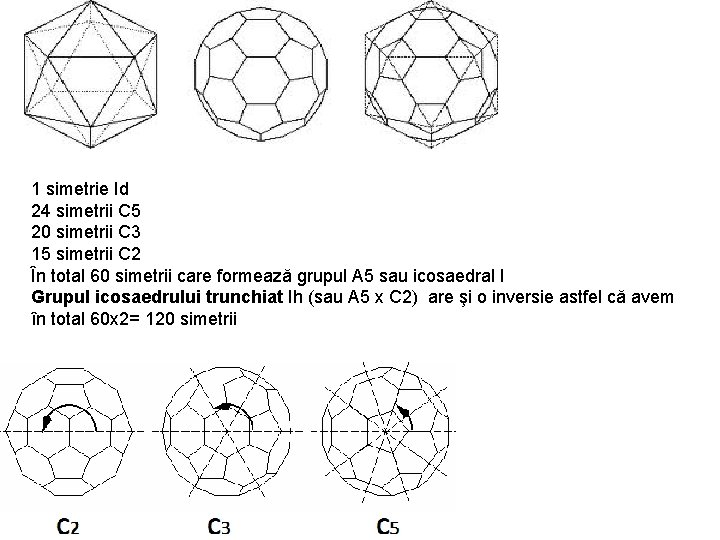
1 simetrie Id 24 simetrii C 5 20 simetrii C 3 15 simetrii C 2 În total 60 simetrii care formează grupul A 5 sau icosaedral I Grupul icosaedrului trunchiat Ih (sau A 5 x C 2) are şi o inversie astfel că avem în total 60 x 2= 120 simetrii