Corpuri geometrice arii i volume Profesor MARIUS FRATILA

Corpuri geometrice arii şi volume Profesor : MARIUS FRATILA Scoala cu clasele I-VIIII Ulmeni, judetul Buzau

Corpuri geometrice Poliedre: • Prisma • Piramida • Trunchiul de piramidă

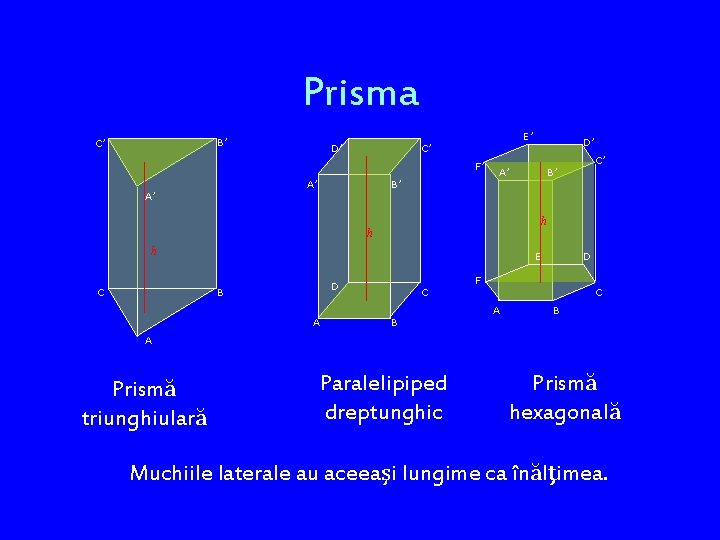
Prisma B’ C’ D’ E’ C’ F’ A’ A’ B’ A’ h E D B A C’ B’ h h C D’ C B D F C A B A Prismă triunghiulară Paralelipiped dreptunghic Prismă hexagonală Muchiile laterale au aceeaşi lungime ca înălţimea.

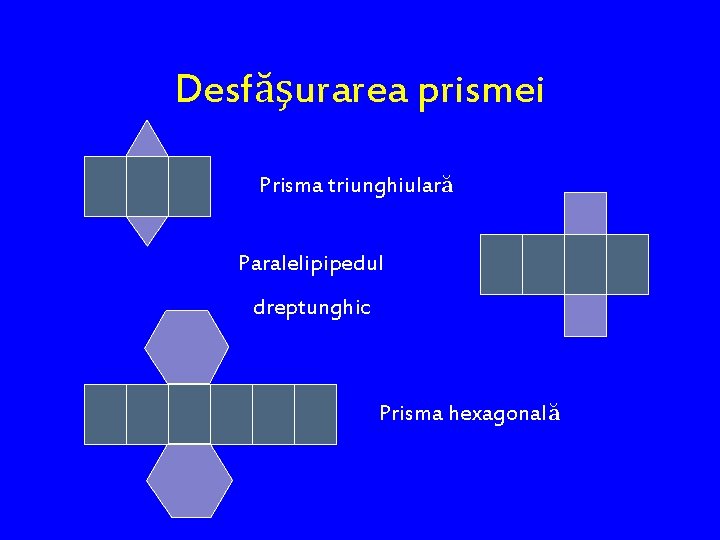
Desfăşurarea prismei Prisma triunghiulară Paralelipipedul dreptunghic Prisma hexagonală

Aria şi volumul prismei Orice prismă are două baze, care pot fi triunghiuri, patrulatere, hexagoane, sau orice alt poligon, şi un număr de feţe laterale egal cu numărul laturilor poligonului de bază. În cazul prismei drepte, aceste feţe laterale sunt dreptunghiuri. Aria unei astfel de feţe laterale este produsul dintre lungimea muchiei corespunzătoare a bazei şi înălţimea prismei. Aria tuturor feţelor laterale este egală cu produsul dintre perimetrul bazei şi înălţimea prismei. Al = P b · h Pentru a calcula aria totală trebuie să luăm în calcul şi aria celor două baze congruente At = Al + 2 Ab. De multe ori, baza este un poligon regulat. Pentru a-ţi reaminti formulelele de calcul ale ariei poligoanelor regulate, urmareste mai departe.

Volumul prismei este egal cu produsul dintre aria bazei şi înălţimea prismei: V = Ab · h.

Paralelipipedul dreptunghic este un caz particular de prismă patrulateră dreaptă. Toate feţele paralelipipedului dreptunghic sunt dreptunghiuri. Paralelipipedul dreptunghic are trei dimensiuni: lungime (L), lăţime (l) şi înălţime (h). Aria totală este suma ariilor celor şase feţe ale paralelipipedului, două câte două congruente: d At = 2 L · l + 2 L · h + 2 l · h. h Volumul său este egal cu produsul celor trei dimensiuni: V = L · l · h. Pătratul lungimii diagonalei paralelipipedului dreptunghic este suma pătratelor lungimilor celor trei dimensiuni ale sale: d 2 = L 2 + l 2 + h 2 Această formulă se mai numeşte şi teorema lui Pitagora în spaţiu. l L

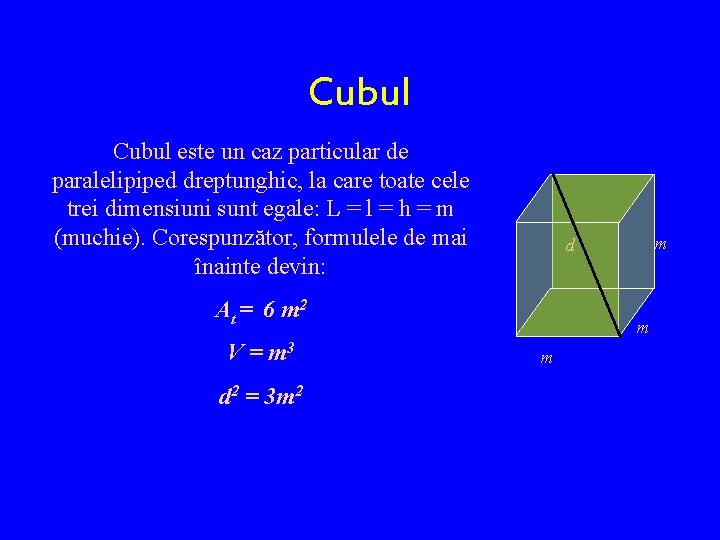
Cubul este un caz particular de paralelipiped dreptunghic, la care toate cele trei dimensiuni sunt egale: L = l = h = m (muchie). Corespunzător, formulele de mai înainte devin: At = 6 m 2 V = m 3 d 2 = 3 m 2 m d m m

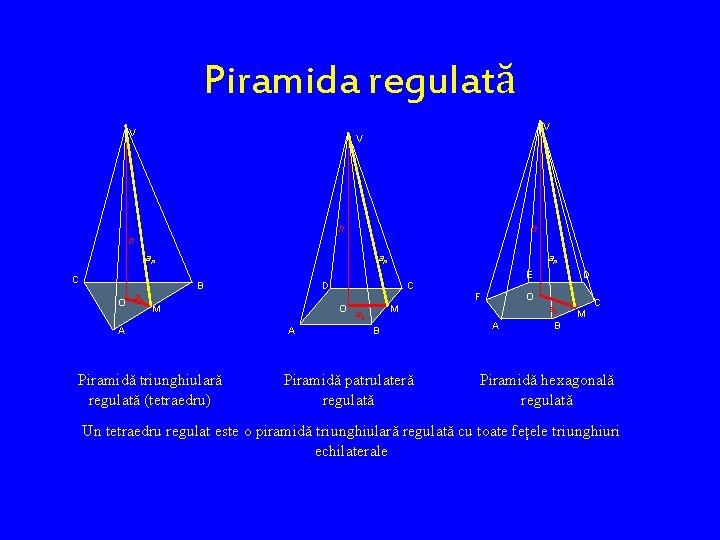
Piramida regulată V V V h h h ap ap ap E C B O ab D F M A Piramidă triunghiulară regulată (tetraedru) O A D C O M ab B Piramidă patrulateră regulată ab A C M B Piramidă hexagonală regulată Un tetraedru regulat este o piramidă triunghiulară regulată cu toate fețele triunghiuri echilaterale

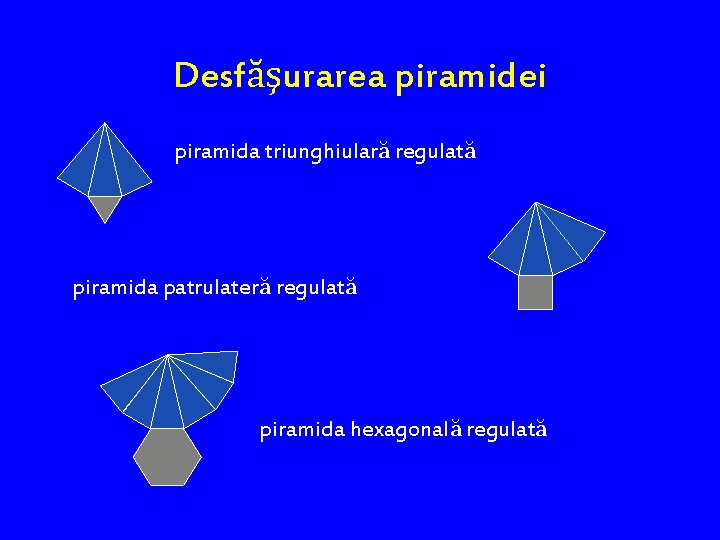
Desfăşurarea piramidei piramida triunghiulară regulată piramida patrulateră regulată piramida hexagonală regulată

Aria şi volumul piramidei regulate Piramidele au o singură bază, care poate fi orice poligon, şi un număr de feţe laterale egal cu numărul laturilor poligonului de bază. În cazul piramidelor regulate, toate aceste feţe laterale sunt triunghiuri isoscele congruente, ale căror baze sunt reprezentate de muchiile bazei piramidei, şi ale căror înălţimi sunt apoteme ale piramidei. Prin urmare, aria unei astfel de feţe laterale este semiprodusul dintre lungimea muchiei bazei piramidei şi cea a apotemei, iar aria laterală, sumă a ariilor tuturor feţelor laterale, este: Al = Pb · ap / 2 Aria totală este suma ariei laterale cu aria bazei unice: At = A b + A l Fiind poligon regulat, aria bazei se poate calcula cu formula: Ab = Pb · ab / 2, de unde rezultă că, pentru a calcula aria totală a unei piramide, putem utiliza şi formula: At = Pb ·( ap + ab) / 2

Volumul piramidei reprezintă o treime din produsul ariei bazei şi lungimea înălţimii piramidei: V = Ab · h / 3 Apotema bazei, apotema piramidei şi înălţimea piramidei sunt legate prin formula: ap 2 = ab 2 + h 2

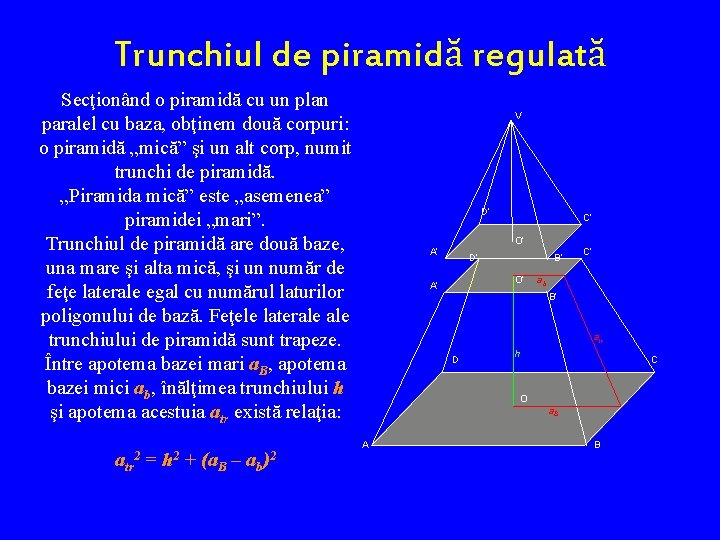
Trunchiul de piramidă regulată Secţionând o piramidă cu un plan paralel cu baza, obţinem două corpuri: o piramidă „mică” şi un alt corp, numit trunchi de piramidă. „Piramida mică” este „asemenea” piramidei „mari”. Trunchiul de piramidă are două baze, una mare şi alta mică, şi un număr de feţe laterale egal cu numărul laturilor poligonului de bază. Feţele laterale trunchiului de piramidă sunt trapeze. Între apotema bazei mari a. B, apotema bazei mici ab, înălţimea trunchiului h şi apotema acestuia atr există relaţia: atr 2 = h 2 + (a. B – ab )2 V D’ C’ O’ A’ D’ B’ O’ A’ C’ ab B’ atr D h C O a. B A B

Aria laterală a trunchiului de piramidă regulată este suma ariilor feţelor laterale, care au formă de trapez. Aria unei astfel de feţe este: A = (m. B + mb) · atr / 2, unde m. B şi mb sunt lungimile muchiilor bazei mari, respective ale bazei mici. Sumând toate ariile feţelor laterale, obţinem pentru aria laterală formula: Al = (PB + Pb) · atr / 2, unde PB şi Pb sunt perimetrele celor două baze. Aria totală este suma ariei laterale cu ariile celor două baze: At = A l + A B + A b = (PB + Pb) atr / 2 + PB · a. B /2 + Pb · ab / 2 Volumul se calculează cu formula: V = h · (AB + Ab + AB · Ab) / 3 mb ab h a. B m. B atr

Poligoane regulate Poligoanele regulate sunt poligoane ale căror laturi sunt congruente şi ale căror unghiuri sunt congruente. Următoarele aspecte sunt caracteristice poligoanelor regulate: - vârfurile poligoanelor regulate sunt puncte conciclice; cercul determinat de aceste puncte se numeşte cercul circumscris poligonului. - există un cerc tangent tuturor laturilor poligonului; acesta este cercul înscris, raza sa se mai numeşte apotemă (a poligonului regulat). - cele două cercuri menţinonate mai sus sunt concentrice; centrul lor comun se numeşte, pur şi simplu, centrul poligonului. - unghiurile poligonului regulat cu n laturi au măsura 180° · (n - 2) / n. - aria unui poligon regulat se poate calcula cu formula: A = P · a / 2, unde P este perimetrul poligonului şi a este apotema sa. Pentru fiecare din următoarele poligoane regulate, vom nota latura, apotema, raza cercului circumscris şi aria sa cu l, a, r şi A, respectiv.

Triunghiul echilateral r=l· 3/3=2 a a=r/2=l· 3/6 l l=r· 3=2 a· 3 R a A = l 2 · 3 / 4 = r 2 · 3 3 / 4 = a 2 · 3 3

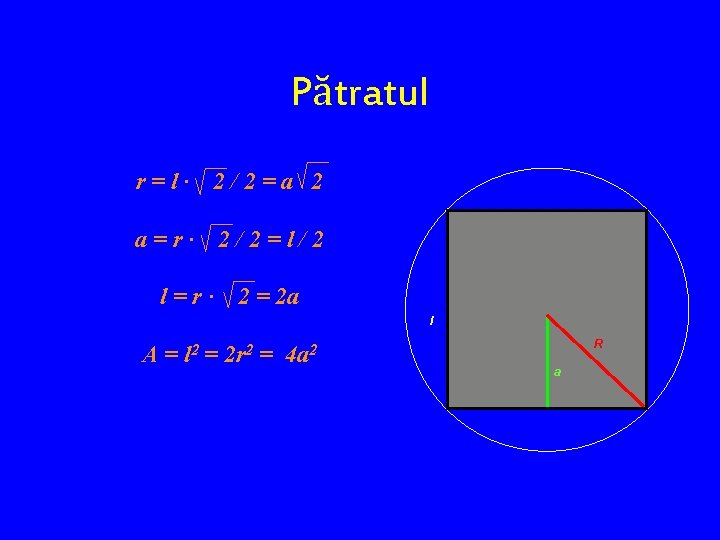
Pătratul r=l· 2/2=a 2 a=r· 2/2=l/2 l=r· 2 = 2 a l A= l 2 = 2 r 2 = 4 a 2 R a

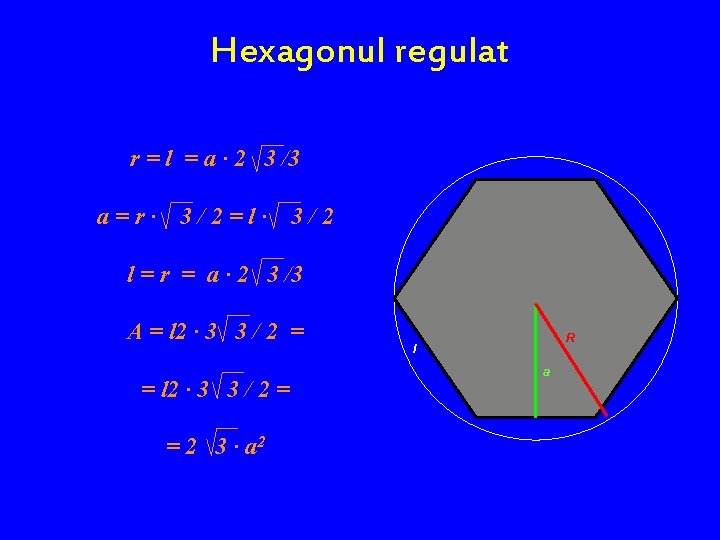
Hexagonul regulat r = l = a · 2 3 /3 a=r· 3/2=l· 3/2 l = r = a · 2 3 /3 A = l 2 · 3 3 / 2 = = 2 3 · a 2 R l a

Probleme 1. Determinaţi aria totală şi volumul tetraedrului regulat de muchie m. 2. Determinaţi volumul tetraedrului care două muchii opuse perpendiculare, de lungime a şi respectiv b, şi ambele perpendiculare pe segmentul de lungime c care uneşte mijloacele lor. 3. Prisma dreaptă ABCA’B’C’ are ca bază triunghiul isoscel ABC (AB = AC). Să se determine măsura unghiului BAC, astfel încât volumul prismei să fie maxim. 4. Calculaţi aria laterală, aria totală şi volumul unei piramide triunghiulare / patrulatere / hexagonale regulate, cunoscând măsura unghiului diedru format de muchia laterală cu planul bazei / măsura unghiului format de o muchie laterală şi una din laturile pe care cade.