GEOMETRIE Clasa a VIa PATRULATERE PATRULATER poligonul cu

GEOMETRIE Clasa a VI-a PATRULATERE

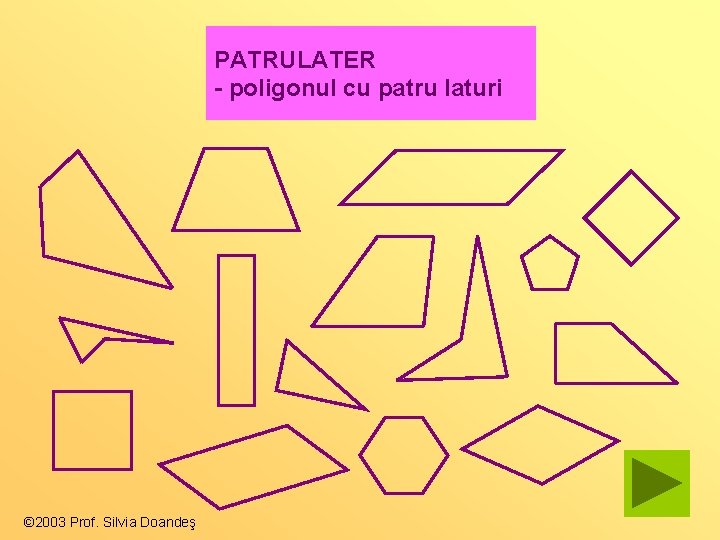
PATRULATER - poligonul cu patru laturi © 2003 Prof. Silvia Doandeş

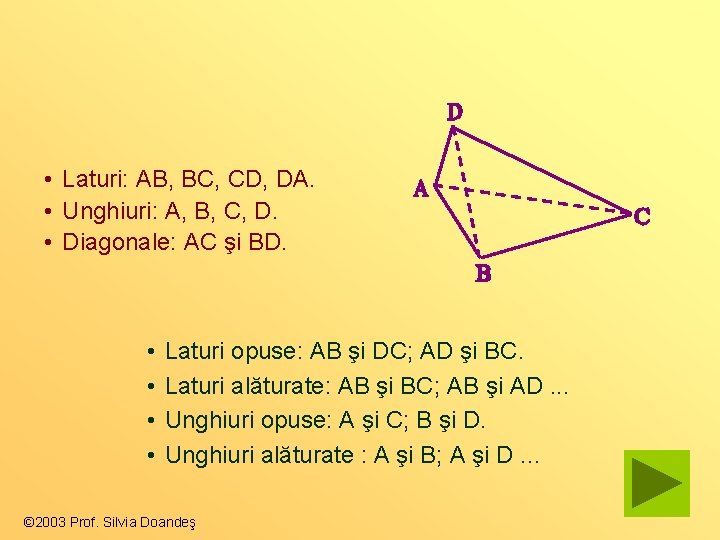
• Laturi: AB, BC, CD, DA. • Unghiuri: A, B, C, D. • Diagonale: AC şi BD. • • Laturi opuse: AB şi DC; AD şi BC. Laturi alăturate: AB şi BC; AB şi AD. . . Unghiuri opuse: A şi C; B şi D. Unghiuri alăturate : A şi B; A şi D. . . © 2003 Prof. Silvia Doandeş

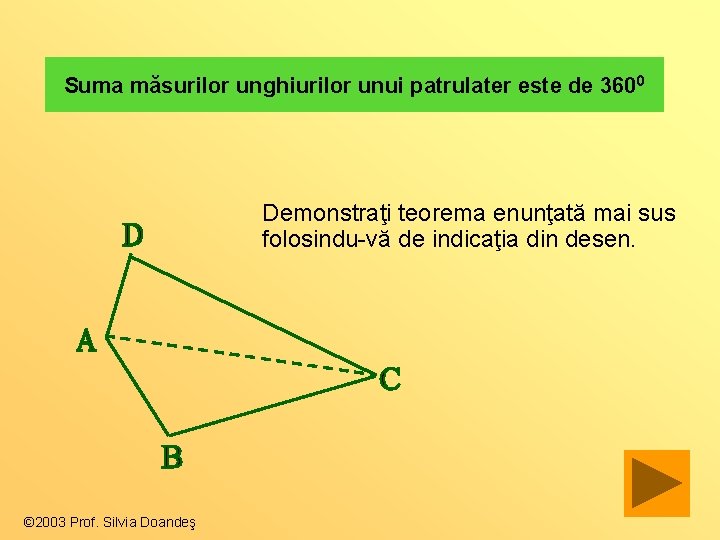
Suma măsurilor unghiurilor unui patrulater este de 3600 Demonstraţi teorema enunţată mai sus folosindu-vă de indicaţia din desen. © 2003 Prof. Silvia Doandeş

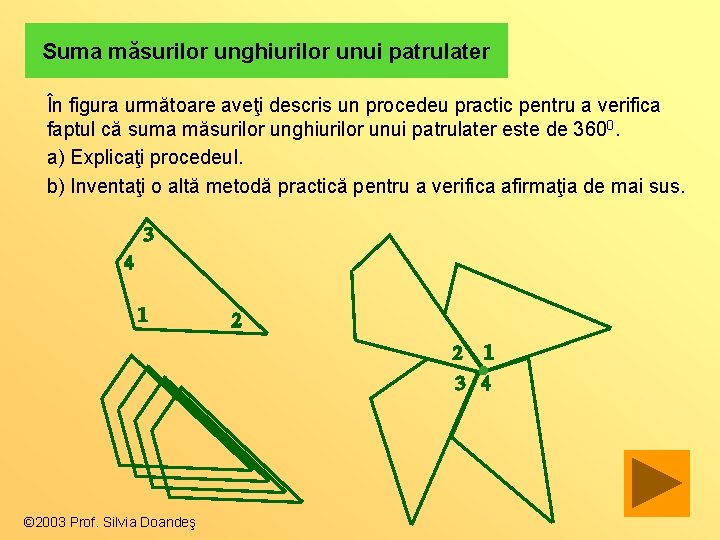
Suma măsurilor unghiurilor unui patrulater În figura următoare aveţi descris un procedeu practic pentru a verifica faptul că suma măsurilor unghiurilor unui patrulater este de 3600. a) Explicaţi procedeul. b) Inventaţi o altă metodă practică pentru a verifica afirmaţia de mai sus. © 2003 Prof. Silvia Doandeş

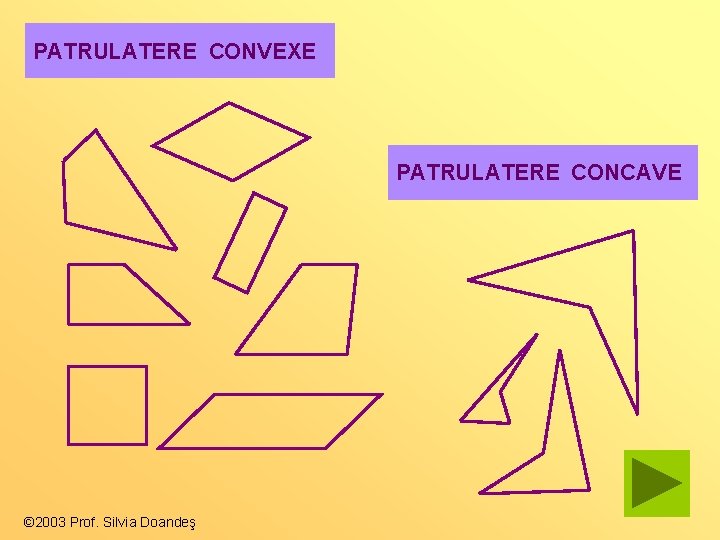
PATRULATERE CONVEXE PATRULATERE CONCAVE © 2003 Prof. Silvia Doandeş

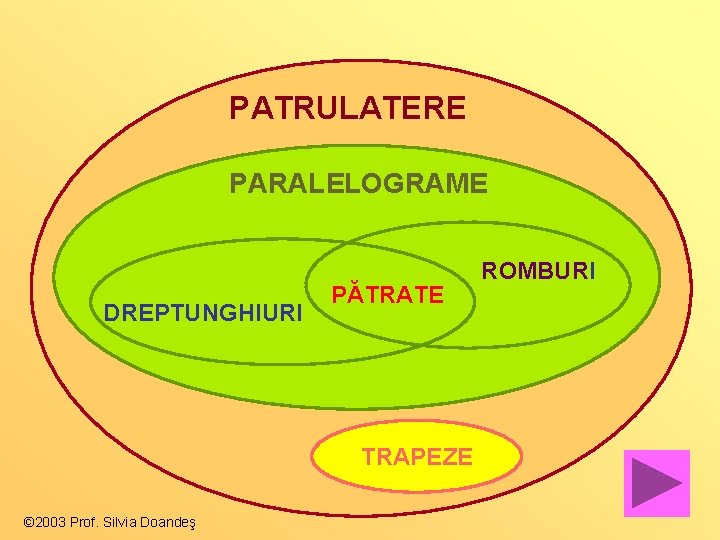
PATRULATERE PARALELOGRAME DREPTUNGHIURI PĂTRATE TRAPEZE © 2003 Prof. Silvia Doandeş ROMBURI

ţi ii m e i i ă r ţ r in t t ă f e t s e e n i m D i r o s p m o e e r d E d P i C ţ I T ă m t C u e A i e C r R r P p a I o o R t r S i Ă P c R U i C B h U L G RE © 2003 Prof. Silvia Doandeş

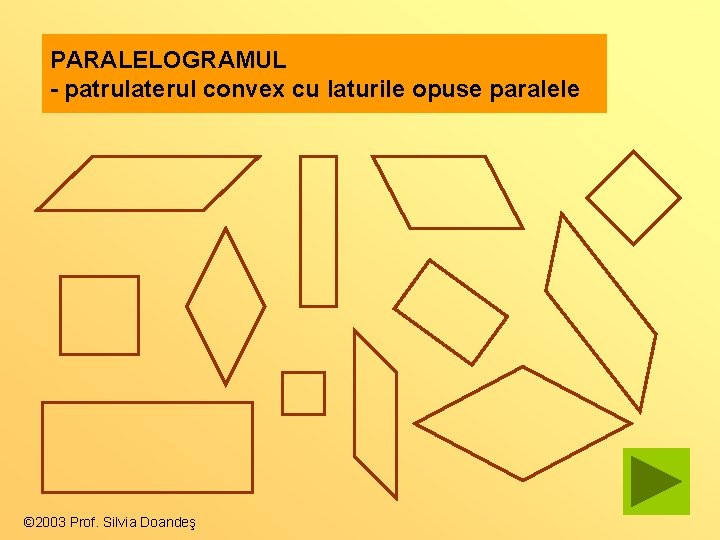
PARALELOGRAMUL - patrulaterul convex cu laturile opuse paralele © 2003 Prof. Silvia Doandeş

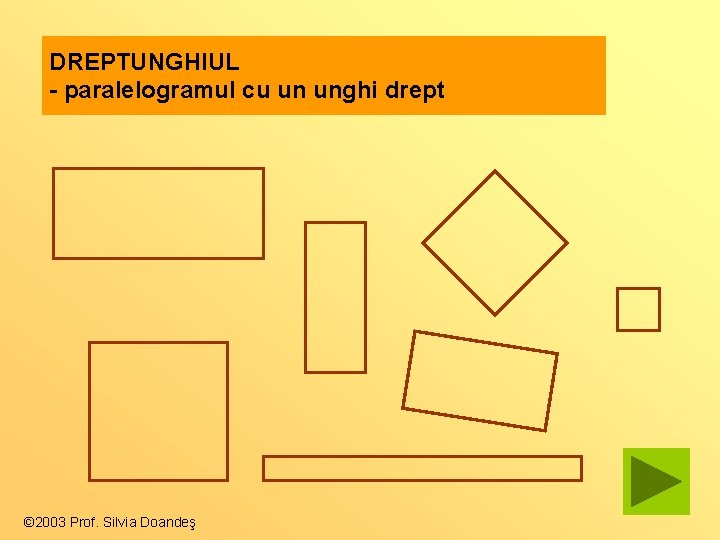
DREPTUNGHIUL - paralelogramul cu un unghi drept © 2003 Prof. Silvia Doandeş

ROMBUL - palelogramul cu două laturi consecutive congruente © 2003 Prof. Silvia Doandeş

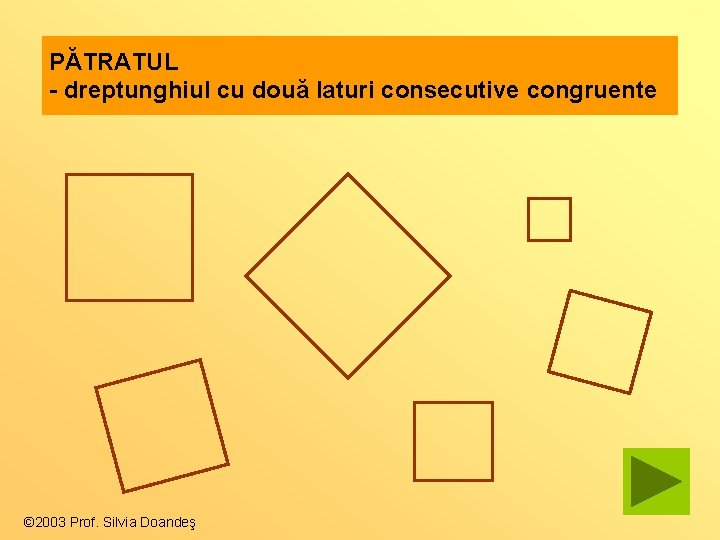
PĂTRATUL - dreptunghiul cu două laturi consecutive congruente © 2003 Prof. Silvia Doandeş

TRAPEZUL -patrulater cu două laturi opuse paralele şi două laturi opuse neparalele © 2003 Prof. Silvia Doandeş

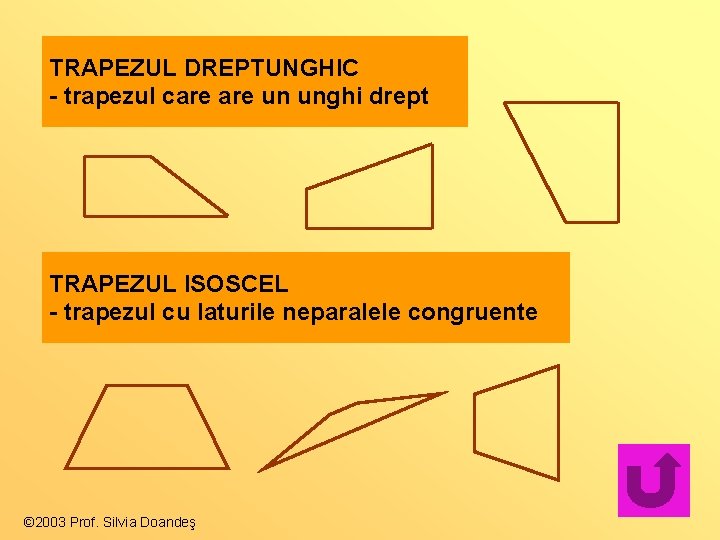
TRAPEZUL DREPTUNGHIC - trapezul care un unghi drept TRAPEZUL ISOSCEL - trapezul cu laturile neparalele congruente © 2003 Prof. Silvia Doandeş

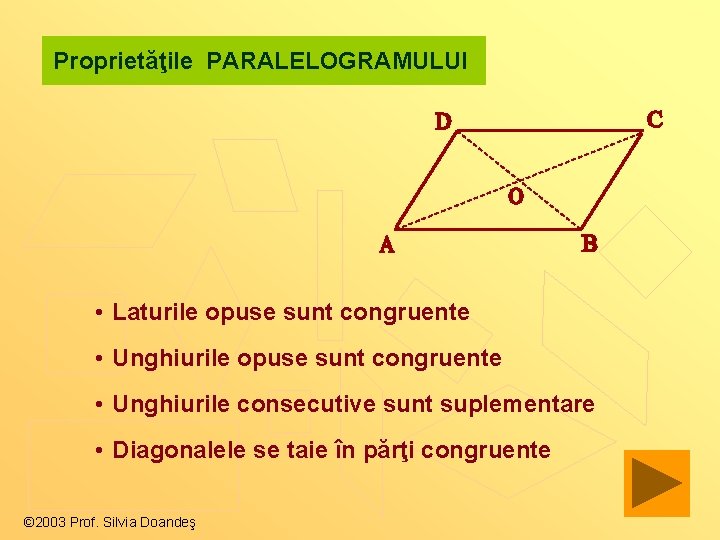
Proprietăţile PARALELOGRAMULUI • Laturile opuse sunt congruente • Unghiurile consecutive sunt suplementare • Diagonalele se taie în părţi congruente © 2003 Prof. Silvia Doandeş

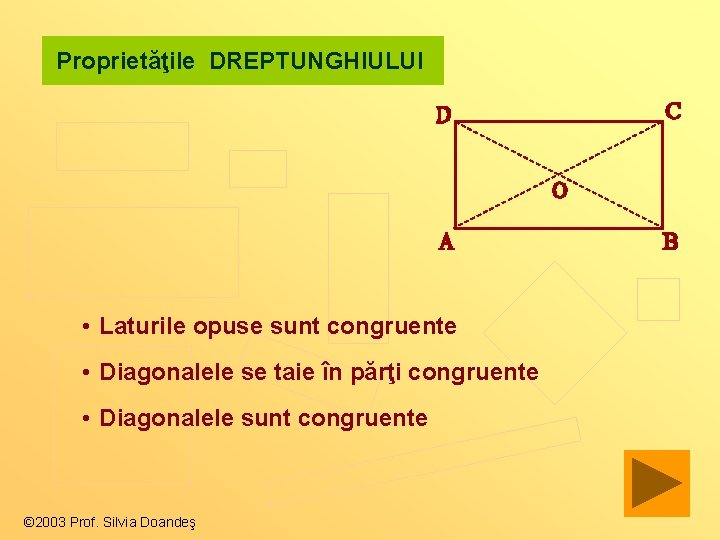
Proprietăţile DREPTUNGHIULUI • Laturile opuse sunt congruente • Diagonalele se taie în părţi congruente • Diagonalele sunt congruente © 2003 Prof. Silvia Doandeş

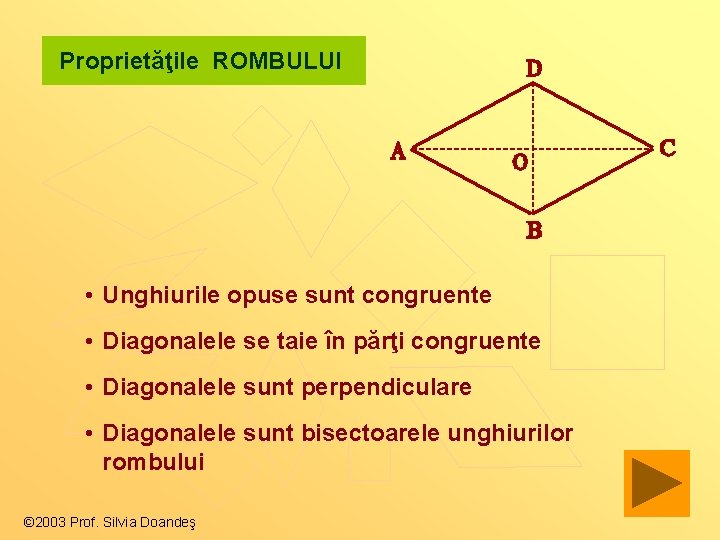
Proprietăţile ROMBULUI • Unghiurile opuse sunt congruente • Diagonalele se taie în părţi congruente • Diagonalele sunt perpendiculare • Diagonalele sunt bisectoarele unghiurilor rombului © 2003 Prof. Silvia Doandeş

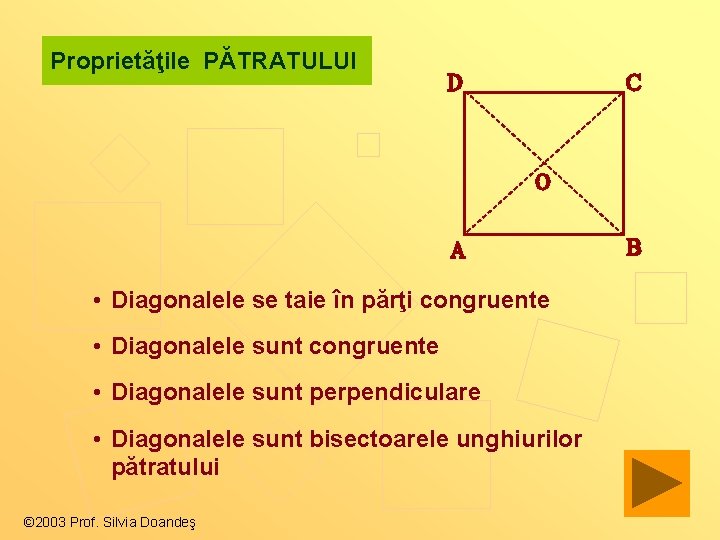
Proprietăţile PĂTRATULUI • Diagonalele se taie în părţi congruente • Diagonalele sunt perpendiculare • Diagonalele sunt bisectoarele unghiurilor pătratului © 2003 Prof. Silvia Doandeş

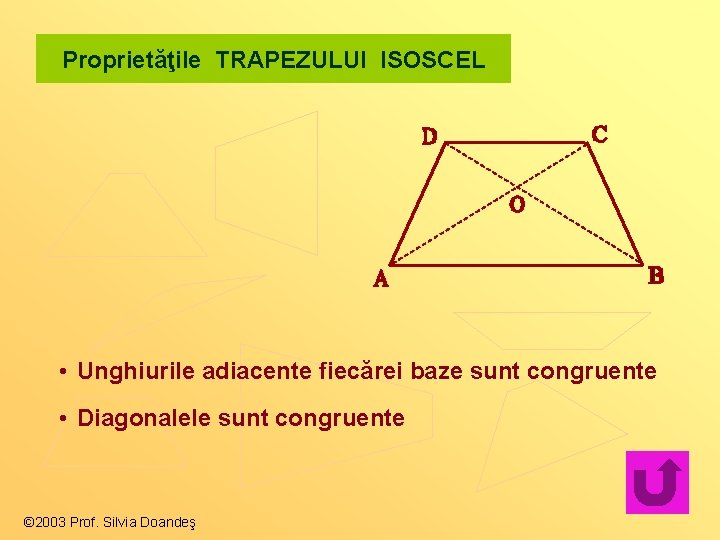
Proprietăţile TRAPEZULUI ISOSCEL • Unghiurile adiacente fiecărei baze sunt congruente • Diagonalele sunt congruente © 2003 Prof. Silvia Doandeş

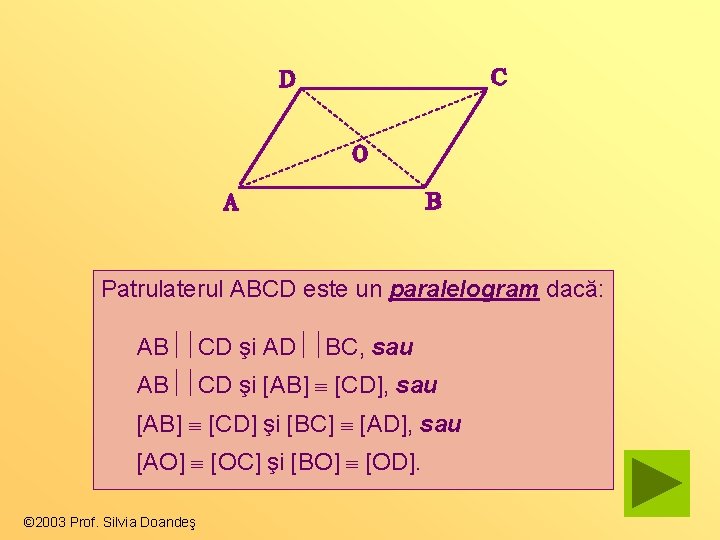
Patrulaterul ABCD este un paralelogram dacă: AB CD şi AD BC, sau AB CD şi [AΒ] [CD], sau [AB] [CD] şi [ΒC] [AD], sau [AO] [OC] şi [ΒO] [OD]. © 2003 Prof. Silvia Doandeş

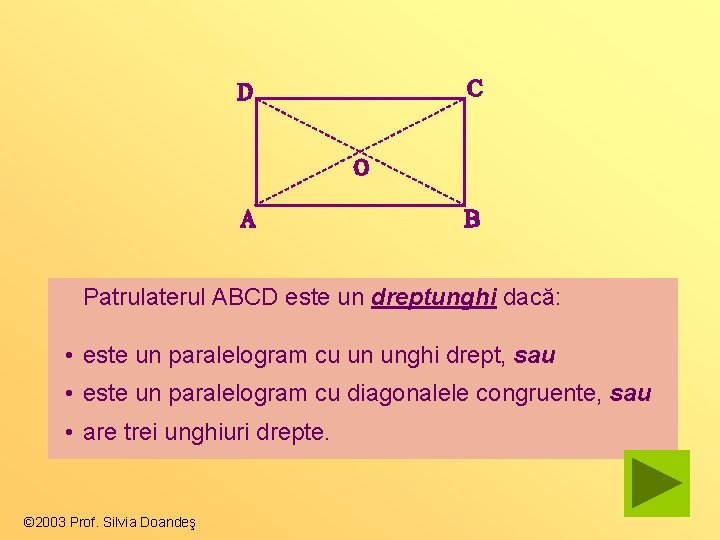
Patrulaterul ABCD este un dreptunghi dacă: • este un paralelogram cu un unghi drept, sau • este un paralelogram cu diagonalele congruente, sau • are trei unghiuri drepte. © 2003 Prof. Silvia Doandeş

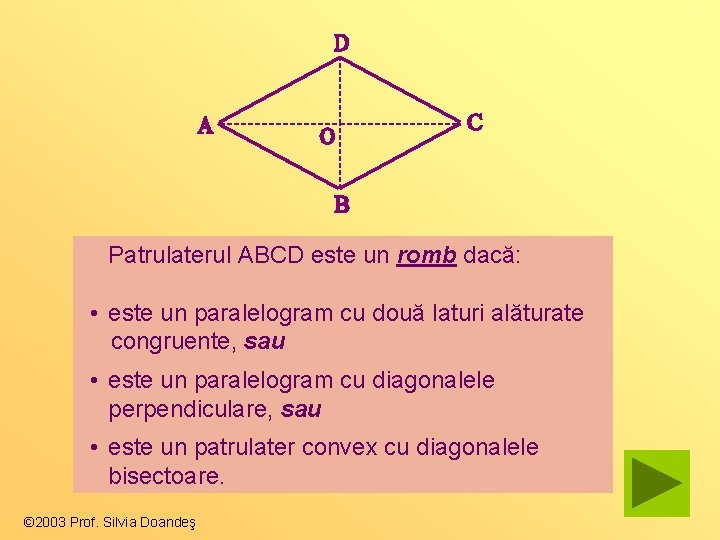
Patrulaterul ABCD este un romb dacă: • este un paralelogram cu două laturi alăturate congruente, sau • este un paralelogram cu diagonalele perpendiculare, sau • este un patrulater convex cu diagonalele bisectoare. © 2003 Prof. Silvia Doandeş

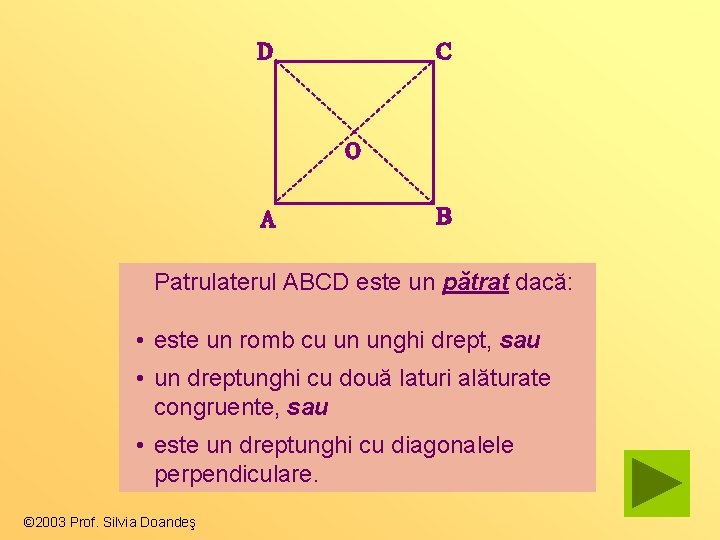
Patrulaterul ABCD este un pătrat dacă: • este un romb cu un unghi drept, sau • un dreptunghi cu două laturi alăturate congruente, sau • este un dreptunghi cu diagonalele perpendiculare. © 2003 Prof. Silvia Doandeş

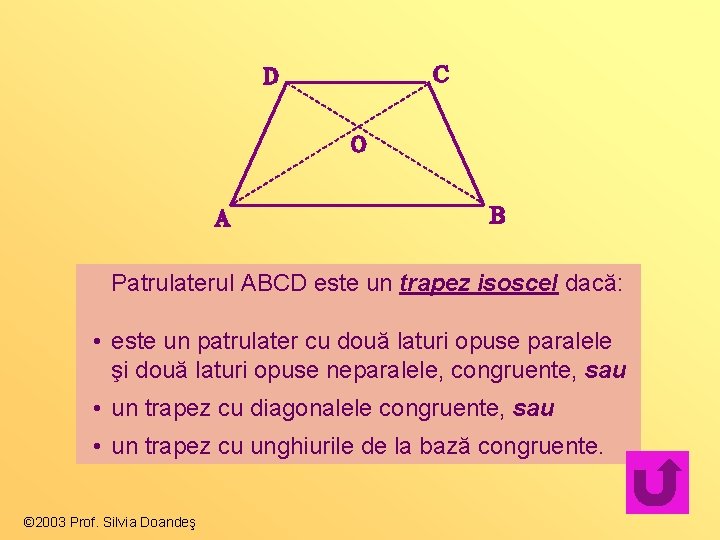
Patrulaterul ABCD este un trapez isoscel dacă: • este un patrulater cu două laturi opuse paralele şi două laturi opuse neparalele, congruente, sau • un trapez cu diagonalele congruente, sau • un trapez cu unghiurile de la bază congruente. © 2003 Prof. Silvia Doandeş

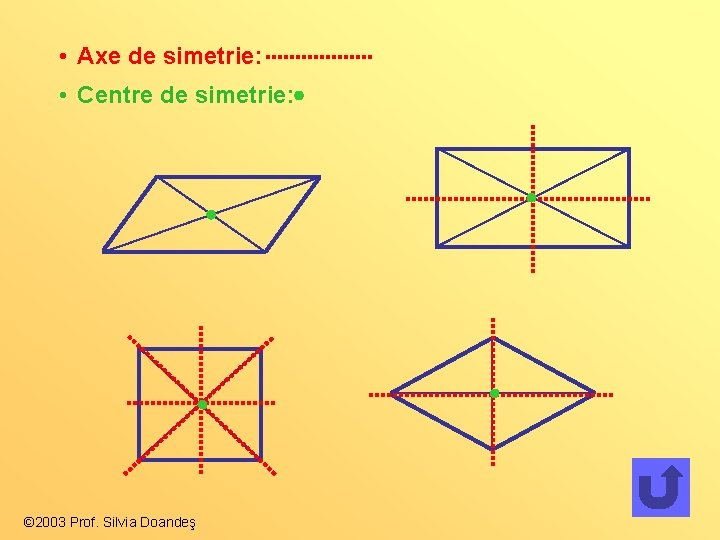
• Axe de simetrie: • Centre de simetrie: © 2003 Prof. Silvia Doandeş

LUCRĂRI PRACTICE Găsiţi modalităţi de pliere pentru a obţine: 1) un pătrat dintr-o foaie de hârtie dreptunghiulară; 2) un paralelogram dintr-o foaie de hârtie dreptunghiulară; 3) un dreptunghi dintr-un paralelogram; 4) un romb de latură maximă dintr-un paralelogram. © 2003 Prof. Silvia Doandeş

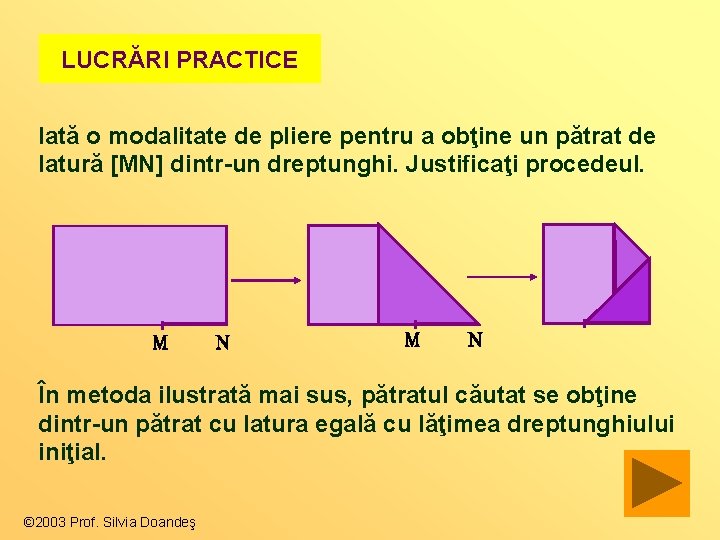
LUCRĂRI PRACTICE Iată o modalitate de pliere pentru a obţine un pătrat de latură [MN] dintr-un dreptunghi. Justificaţi procedeul. În metoda ilustrată mai sus, pătratul căutat se obţine dintr-un pătrat cu latura egală cu lăţimea dreptunghiului iniţial. © 2003 Prof. Silvia Doandeş

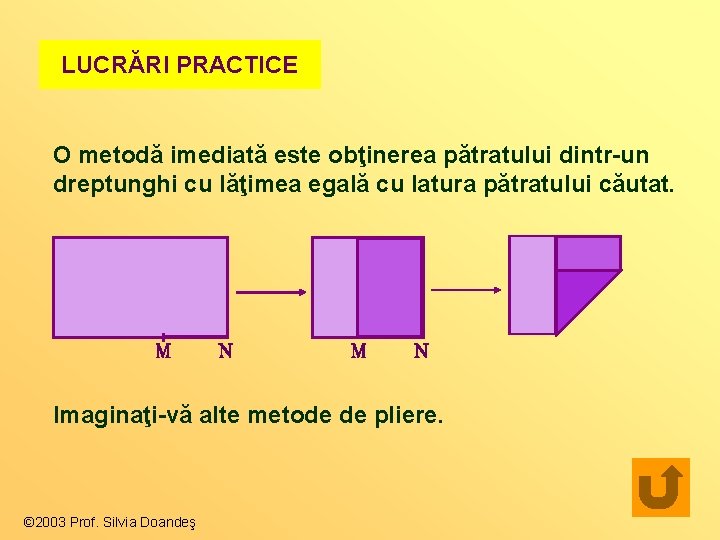
LUCRĂRI PRACTICE O metodă imediată este obţinerea pătratului dintr-un dreptunghi cu lăţimea egală cu latura pătratului căutat. Imaginaţi-vă alte metode de pliere. © 2003 Prof. Silvia Doandeş

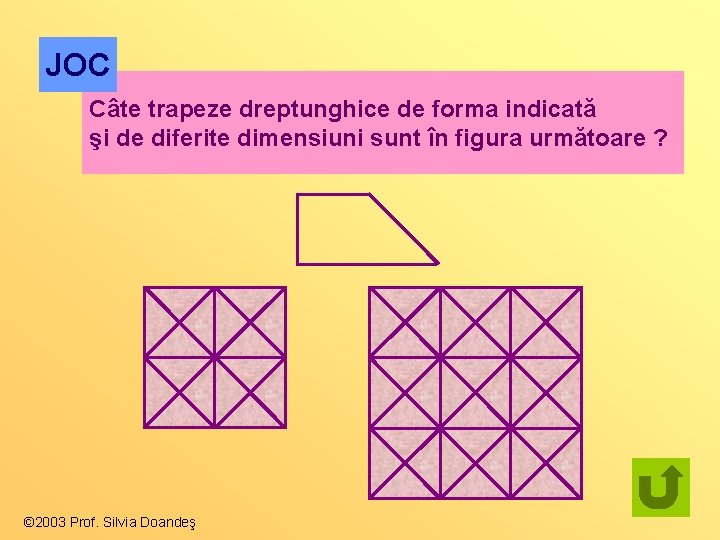
JOC Câte trapeze dreptunghice de forma indicată şi de diferite dimensiuni sunt în figura următoare ? © 2003 Prof. Silvia Doandeş

GHICITOARE • Gândeşte-te la unul din cele cinci patrulatere studiate. • Dacă răspunzi corect la următoarele întrebări, atunci eu pot ghici la ce patrulater te-ai gândit. © 2003 Prof. Silvia Doandeş

1 Are laturile opuse paralele ? DA © 2003 Prof. Silvia Doandeş NU

2 Are diagonalele perpendiculare ? DA © 2003 Prof. Silvia Doandeş NU

3 Are unghi drept ? DA © 2003 Prof. Silvia Doandeş NU

3 Are unghi drept ? DA © 2003 Prof. Silvia Doandeş NU

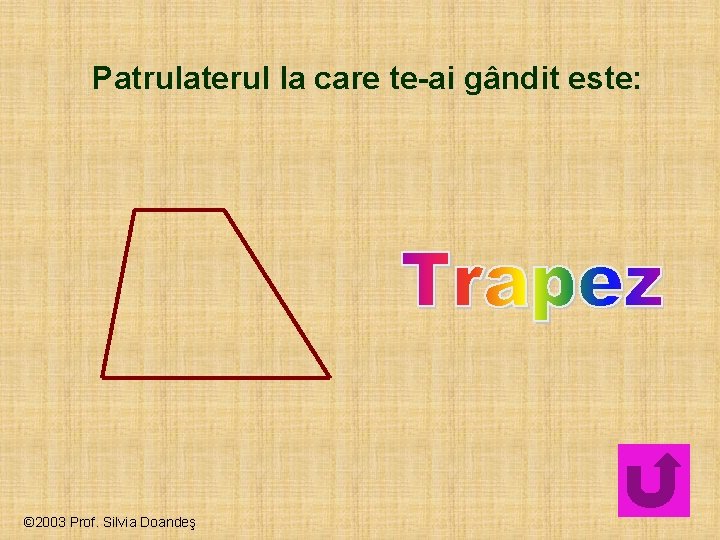
Patrulaterul la care te-ai gândit este: © 2003 Prof. Silvia Doandeş

Patrulaterul la care te-ai gândit este: © 2003 Prof. Silvia Doandeş

Patrulaterul la care te-ai gândit este: © 2003 Prof. Silvia Doandeş

Patrulaterul la care te-ai gândit este: © 2003 Prof. Silvia Doandeş

Patrulaterul la care te-ai gândit este: © 2003 Prof. Silvia Doandeş

FELICITĂRI ! AI AJUNS LA FINAL. ÎNAPOI IEŞIRE