Numerical Solutions of ODE Dr Asaf Varol 1

Numerical Solutions of ODE Dr. Asaf Varol 1

What is ODE and PDE • A differential equation is an equation which involves derivatives of one or more dependent variables. If there is only one independent variable involved in the equation(s), then the derivatives are referred to as ordinary derivatives. If, however, there is more than one independent variable in the equation, then partial derivatives (PDE) with respect to each of the independent variables are used. 2

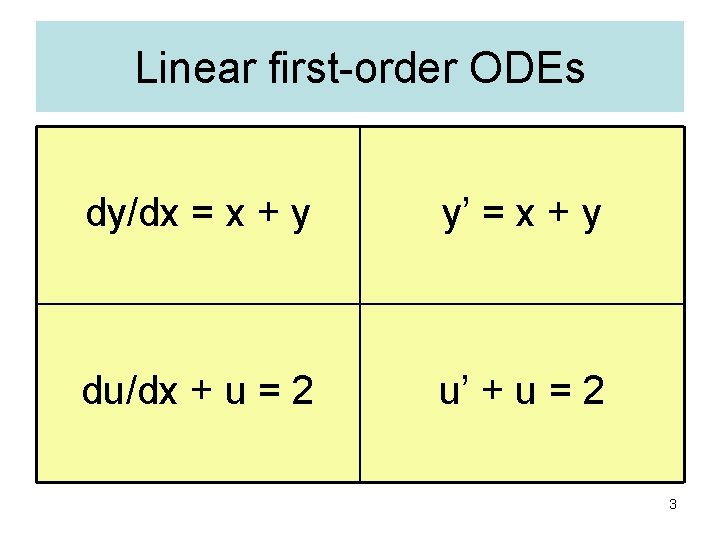
Linear first-order ODEs dy/dx = x + y y’ = x + y du/dx + u = 2 u’ + u = 2 3

Non-Linear first-order ODEs dy/dx = x + cos(y) y’ = x + cos(y) du/dt + u 2 = 2 u’ + u 2 = 2 4

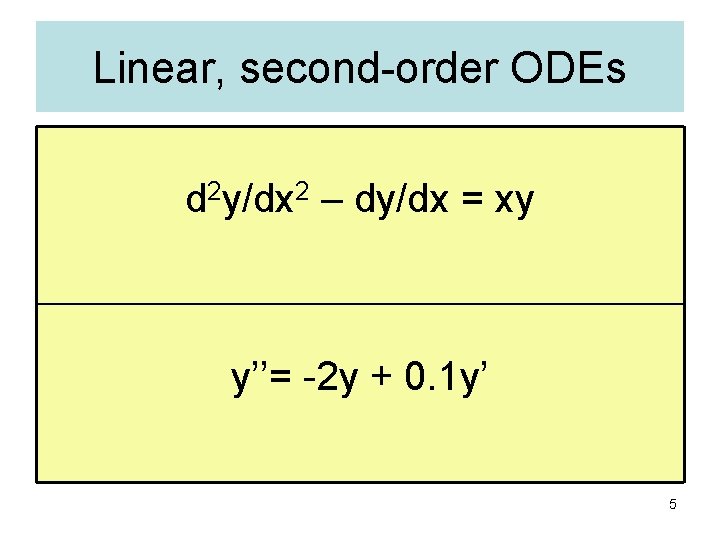
Linear, second-order ODEs d 2 y/dx 2 – dy/dx = xy y’’= -2 y + 0. 1 y’ 5

Non-Linear, second-order ODEs d 2 y/dx 2 – dy/dx = xy-y y’’= -2 y + 0. 1(y’)2 6

Homogeneous ODEs • Homogeneous ODE is an equation which contains the dependent variable or its derivatives in every term. d 2 y/dx 2 – dy/dx = xy-y y’’= -2 y + 0. 1(y’)2 7

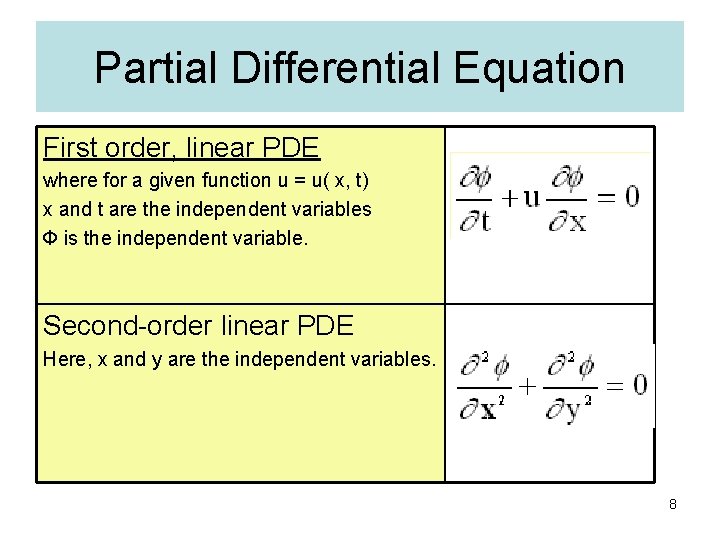
Partial Differential Equation First order, linear PDE where for a given function u = u( x, t) x and t are the independent variables Ф is the independent variable. Second-order linear PDE Here, x and y are the independent variables. 8

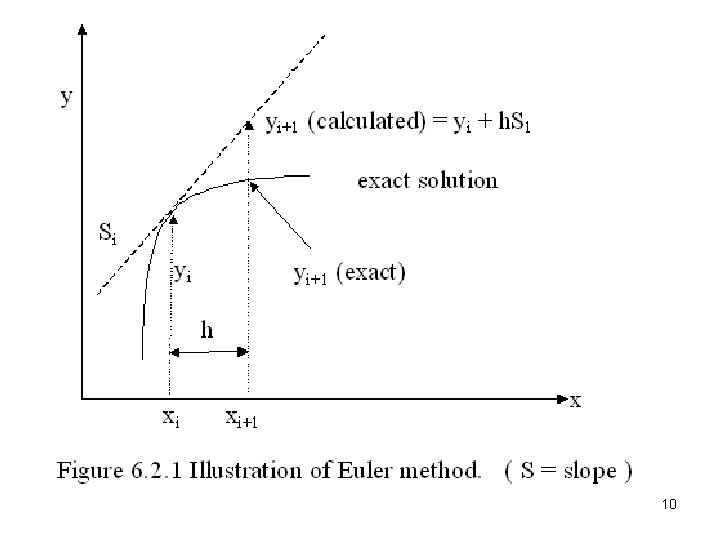
Euler’s Method 9

10

11

12

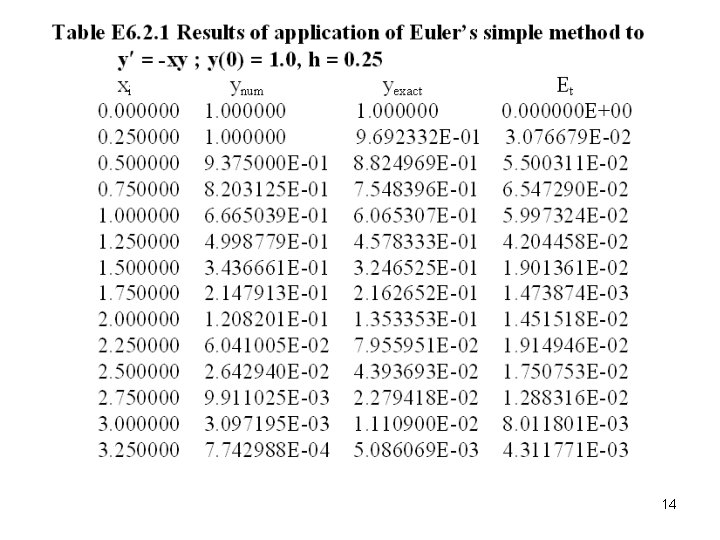
13

14

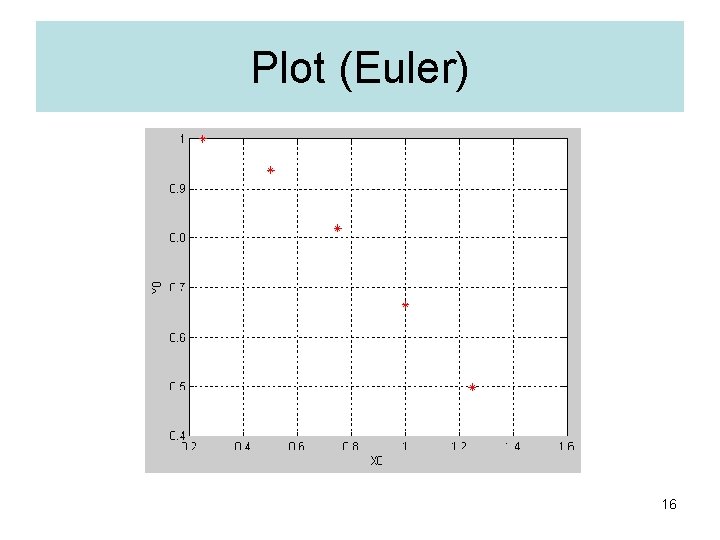
MATLAB (Euler) 15

Plot (Euler) 16

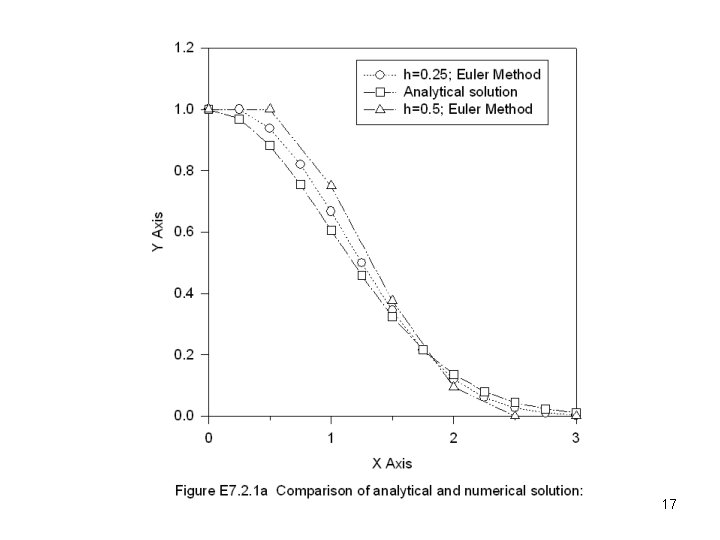
17

Example • EULER METHOD’S • Solving a simple ODE with Euler’s Method • Consider the differential equation y’ = f( x, y ) on a≤ x≥ b. Let • y’ = x + y; 0 ≤ x ≥ 1 a = 0, b = 1, y(0) = 2. • First, we find the approximate solution for h=0. 5 (n = 2), a very large step size. • The approximation at x 1 = 0. 5 is • y 1=y 0 + h (x 0 + y 0)= 2. 0 + 0. 5 (0. 0 + 2. 0) = 3. 0 • Next, we find the approximate solution, we use n = 20 intervals, so that h = 0. 05. 18

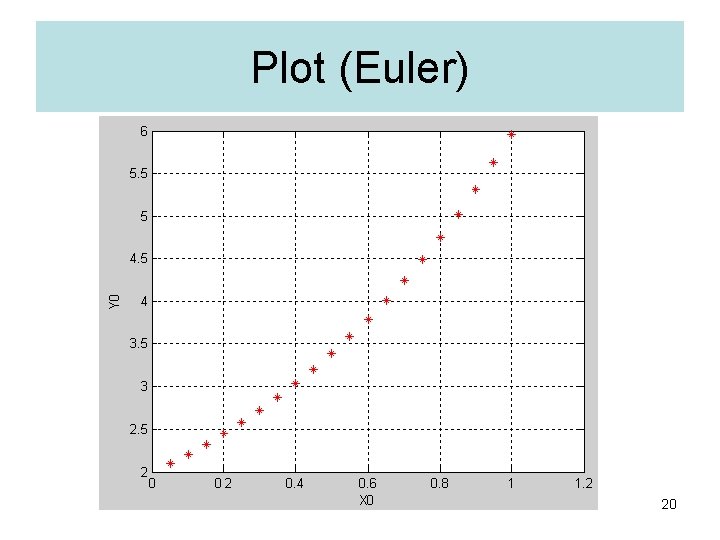
Solution with MATLAB (Euler) 19

Plot (Euler) 20

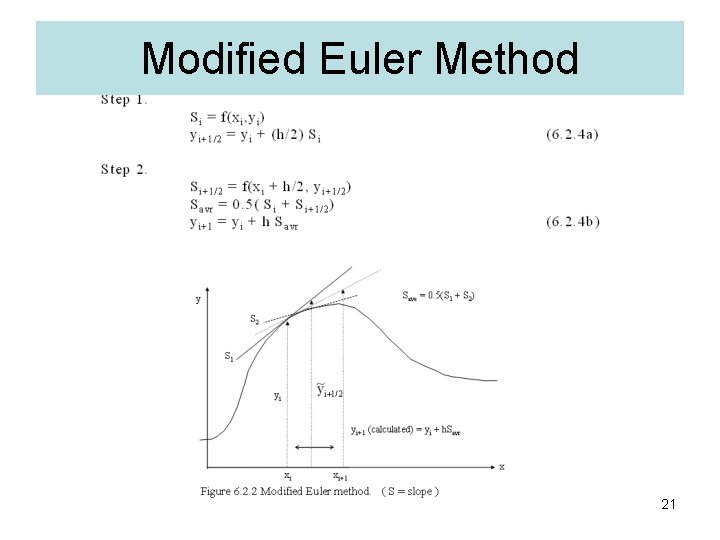
Modified Euler Method 21

Higher Order Taylor Methods • One way to obtain a better solution technique is to use more terms in the Taylor series for y in order to obtain higher order truncation error. For example, a second-order Taylor method uses • y(x+h)=y(x)+hy’(x)+(h 2/2)y’’(x)+O(h 3) • O(h 3) is the local truncation error 22

Solving a Simple ODE with Taylor’s Method • Consider the differential equation • y’=x + y; 0≤ x ≤ 1 with a initial condition y(0) = 2. • To apply the second order Taylor method to the equation, we find • y’’=d/dx( x+ y) = 1 + y’ = 1 + x + y • This gives the approximation formula • y(x + h)=y(x)+hy’(x)+(h 2/2)y’’(x) 23

Cont’d yi+1=yi+h(xi+yi)+(h 2/2)(1+xi+yi) For n=2 (h=0. 5), we find y 1=y 0+h(x 0+y 0)+(h 2/2)(1+x 0+y 0)= =2+0. 5(0+2)+((. 5)2/2)(1+0+2)=3. 375 y 2=y 1+h(x 1+y 1)+(h 2/2)(1+x 1+y 1)= =3. 375+0. 5(0. 5+3. 375)+((0. 5)2/2)(1+0. 5+3. 375)=5. 9219 24

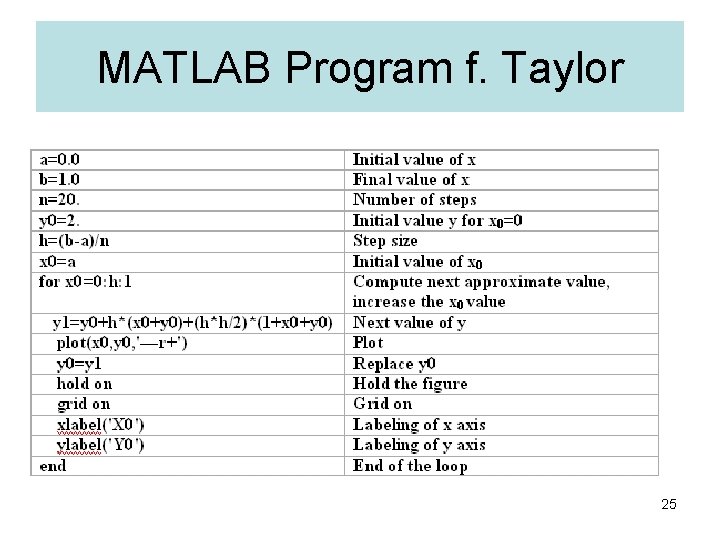
MATLAB Program f. Taylor 25

Plot (Taylor) 26

RUNGE-KUTTA METHODS • Runge-Kutta methods are the most popular methods used in engineering applications because of their simplicity and accuracy. One of the simplest Runge. Kutta methods is based on approximating the value of y at xi + h/2 by taking one-half of the change in y that is given by Euler’s method and adding that on to current value yi. This method is known as the midpoint method. 27

Midpoint Method • k 1=hf(xi, yi) Change in y given by Euler’s method. • k 2=hf(xi+0. 5 h, yi+0. 5 k 1) Change in y using slope estimate at midpoint 28

Solving a Simple ODE with Midpoint Method • Consider the differential equation • y’=x + y; 0≤ x ≤ 1 with a initial condition (a=0. 0, b=0. 0), y(0) = 2. • First, we find the approximate solution for h=0. 5 (n=2), a very large step size. • k 1=hf(x 0, y 0)=0. 5(0. 0+2. 0)=1. 0 • k 2=hf(x 0+0. 5 h, y 0+0. 5 k 1)=0. 5(0. 0+0. 5*0. 5+2. 0+0. 5*1. 0)=1. 375 • Y 1=y 0+k 2=2. 0+1. 375=3. 375 • Next, we find the approximate solution y 2 at point x 2=0. 0+2 h=1. 0 29

Cont’d • k 1=hf(x 1, y 1)=0. 5(0. 5+3. 375)=1. 9375 • k 2=hf(x 1+0. 5 h, y 1+0. 5 k 1)=0. 5(0. 5+0. 5*0. 5+3. 375+0. 5*1. 93 75)=2. 547 y 2=y 1+k 2=3. 375+2. 5469=5. 922 30

MATLAB Prog. f. Midpoint 31

Plot (Midpoint) 32

References • • • Celik, Ismail, B. , “Introductory Numerical Methods for Engineering Applications”, Ararat Books & Publishing, LCC. , Morgantown, 2001 Fausett, Laurene, V. “Numerical Methods, Algorithms and Applications”, Prentice Hall, 2003 by Pearson Education, Inc. , Upper Saddle River, NJ 07458 Rao, Singiresu, S. , “Applied Numerical Methods for Engineers and Scientists, 2002 Prentice Hall, Upper Saddle River, NJ 07458 Mathews, John, H. ; Fink, Kurtis, D. , “Numerical Methods Using MATLAB” Fourth Edition, 2004 Prentice Hall, Upper Saddle River, NJ 07458 Varol, A. , “Sayisal Analiz (Numerical Analysis), in Turkish, Course notes, Firat University, 2001 33