Introduction to computing Dr Asaf Varol varol asafgmail

Introduction to computing Dr. Asaf Varol varol. asaf@gmail. com 1

Basic operation performed by a computer • Arithmetic Operations: Addition, subtraction, multiplication and division • Logical operations: the sign or the comparative magnitude of two numbers • Data transfer: Moving data from one location to another in the memory. • Input-output operations: Controlling the reading/writing of information into or out of the computer 2

On Digital Computers Digital computers store numbers in an entity (or unit) called a word which consists of a string of binary digits, or bits. Various number systems are used to represent mathematical numbers. Some commonly used number systems are: hexadecimal (base 16), decimal (base 10), octal (base 8), and binary (base 2). For example, in a decimal system the number 8, 410 is represented in powers of ten as: 8 103 + 4 102 +1 101 + 0 100 = 8000 + 400 + 10 + 0 = 8, 410 3

On Digital Computers (Cont’d) A method known as the doubling procedure is as follows. Given a decimal number N, it can be decomposed as: N = 2 Q 1 + R 1 Q 1 = 2 Q 2 + R 2. . . Qk = 0 + Rk+1 (Q 1 = N/2 - remainder) (Q 2 = Q 1/2 - remainder). . . etc. The corresponding binary number is obtained by writing the remainders Rk+1, Rk, . . . , R 1 in the reverse order as: B = Rk+1 Rk. Rk-1. . . R 1 4

Example Convert the decimal number N = 8, 410, to a binary number. Solution: Perform sequential division by 2 as follows: 8, 410 = (2 4, 205) + 0 65 = (2 32) + 1 4, 205 = (2 2, 102) + 1 32 = (2 16) + 0 2, 102 = (2 1, 051) + 0 16 = (2 8) + 0 1, 051 = (2 525) + 1 8 = (2 4) + 0 525 = (2 262) + 1 4 = (2 2) + 0 262 = (2 131) + 0 2 = (2 1) + 0 131 = (2 65) +1 1 = (2 0) + 1 The binary equivalent of 8, 410 is then given by collecting the remainder digits from the last to the first: 10000011011010 = 1 1213 + 0 212 + 0 211 + 0 210 + 0 29 + 0 28 + 1 27 + 1 26 + 0 25 + 1 24 + 1 23 + 0 22 + 1 21 + 0 20 5

Representations of Numbers are usually represented using the normal form notation. That is, x = m. 10 E for 10 -1 < m < 1 where for x 0, m is called the mantissa and E is the exponent. By convention, the number zero has the normal notation, 0. 100. 6

Significant Digits If a number is written in standard decimal, floating-point form, or in normal form such that: x = 0. d 1 d 2 d 3. . . dk 10 n with d 1 0 and dk 0, we say that this number has k significant digits (or significant figures) which indicates those digits that can be used with a confidence relative to the true value of the number. 7

Significant Digits (Cont’d) Note that the zeros which are used only to shift the decimal point are not counted as significant figures. The leading zeros may or may not be significant. For example, x = 0. 0002815 has 4 significant figures! x = 1, 200 may have 4, 3, or 2 significant figures! Some examples are: 46. 45072800 significant digits) -335. 12 0. 00517 0. 74 = 0. 46450728 102 (with 8, 9, or 10 = -0. 33512 103 (with 5 significant digits) = 0. 517 10 -3 (with 3 significant digits) = 0. 74 100 (with 2 significant digits) 8

Computer Representation of Numbers The decimal equivalent of the binary number represented in Figure 1. 4. 1 is given by: -(0 26 + 0 25 + 0 24 + 1 23 + 0 22 + 1 21 + 1 20) = -(0 + 0 + 8 + 0 + 2 + 1) = -11 Figure 1. 4. 1 Binary representation of an integer using an 8 bit word (or Byte) 9

Example Determine the largest integer that can be represented by an 8 bit machine. Solution: Imax = +(1 26 + 1 25 + 1 24 + 1 23 + 1 22 + 1 21 + 1 20) = +( 64 + 32 + 16 + 8 + 4 + 2 + 1 ) = +(127) = +(27 - 1) In general: Imax = +[2(n -1) - 1]; Imin = -[2(n -1) - 1] For a binary computer utilizing 32 bit words, Imax = 2, 147, 483, 647 10

Floating-Point Representation A floating-point number is written as: x = (sign)m. b(sign)E where m is the mantissa, b is the base (b = 2 for a binary system), and E is the exponent. 11

Example Determine the smallest, positive, nonzero, floating point number that can be represented by an eight bit machine using binary system with one bit spared for the sign of the mantissa, one bit for the sign of the exponent, and two bits for the digits of the exponent: Solution: m = +(0 23 + 0 22 + 0 21 + 1 20) m = +( 0 +0 + 1 )=1 E = -[(1 21) + (1 20)] = -(2+1) = - 3 Number = 1 2 -3 (which is equal to 0. 1250 in decimal system) 12

Errors the approximation of numbers, accuracy, and precision. Neither physical measurements nor arithmetic calculations can be carried out exactly. The engineer's motto should be: “There is nothing which is absolutely correct or exact in science” Accuracy is the measure of how close an estimated value or answer is to its true (or exact) value. Since in many situations this exact value is not known, the accuracy of an answer is usually measured with respect to the best-estimated value. Precision implies how closely the repeatedly measured (or calculated) values of a certain quantity agree with each other. Thus it represents the number of significant figures in representing that quantity as a single average number with a spread (variation) around its mean. 13

Errors True absolute error Et = (true value) - (approximate value) Approximate absolute error Ea = (best estimate) - (approximate value) True relative error et = (true value) - (approximate value) / true value Approximate relative error ea = (best estimate) - (approximate value) / best estimate 14

Errors (Cont’d) For series, sequences, and iterations, approximate error can be defined as: Approximate absolute error (for iterative calculations): Ea = (current value) - (previous value) Approximate relative error (for iterative calculation): ea = ( (current value) - (previous value) )/ current value When the exact value of a quantity is not given (or known), it is not possible to calculate a true error. However, the approximate error can be used to calculate error bounds for an approximate answer. To this end, a theorem called Scarborough criteria can be very useful. Scarborough Criteria If the approximate relative error, ea < 0. 5 10 -m, then the result (or the answer) is correct to at least m significant digits. 15

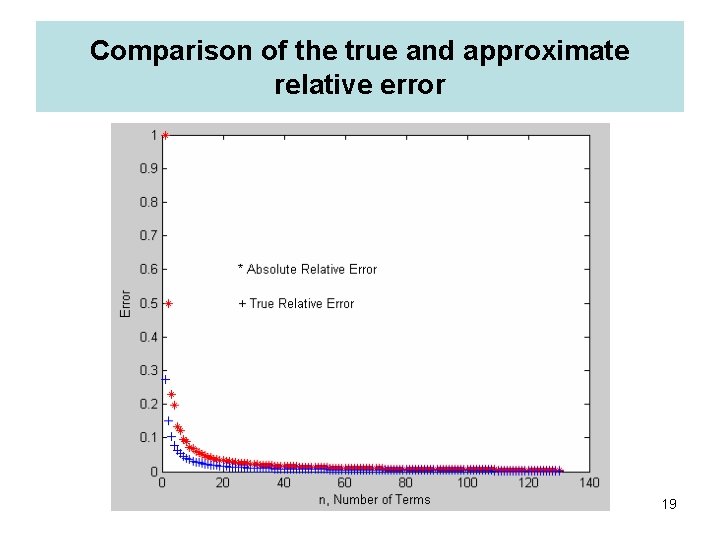
Example E 1. 5. 1 Calculate the number of terms that is necessary to estimate the value of to two significant digits from the Taylor series expansion for Arctan(x) about the base point x = 0. The number = 3. 141592653589793 (to 16 significant digits) is related to this function by: = 4. 0 Arctan(1. 0) Solution: The infinite series (convergent in the range – 1. 0 to 1. 0) is given by: where n = 1, 2, 3, . . . Check your answer by actually calculating from the above series. Plot the true relative error and the approximate relative error as a function of the number of terms. 16

Errors (Cont’d) Note that for such series, the definition of ea reduces to: ea = (current value) - (previous value) / current value ea = last term used / current sum If we assume that the current sum is accurate to two significant digits ( = 3. 1), then: ea 4 (-1)(n+1) x 2 n-1/(2 n-1) /(3. 1) at x = 1 Using Scarborough criteria, ea (4/3. 1)/(2 n-1) < 0. 5 10 -2 Solving this equation for n (by trial and error) gives: n 130 17

Mat. Lab solution 18

Comparison of the true and approximate relative error 19

Computer errors: Round off or Chop off errors Most computers chop off (or simply ignore) the digits beyond their capacity of representing them. That is, when the number of significant digits does not fit into the space allocated for the mantissa, some computers round the number. For example, a computer with a three digit mantissa will represent 68. 501 as 0. 068 E 03 when chopping off is used, or as 0. 069 E 03 when rounding is used. 20

Computer errors: Round off or Chop off errors Subtractive cancellation This error occurs when subtracting two nearly equal numbers. Let us further explain this with an example. Example If x = 40, 000. 01 and y = 40, 000, what is x minus y using a 3 -digit mantissa? Solution: 0. 4000001 x 105 -0. 4000000 x 105 ____________ 0. 000 x 105 = 0. 0 Smearing due to round-off errors Significant errors can occur when adding a large and a small number. For example, adding two temperatures, 0. 4 K to 250 K, using a hypothetical decimal computer with a mantissa of 3 digits, yields: 0. 250 x 10 3 0. 0004 x 103 ____________ 0. 250 x 103 = 250 K 21

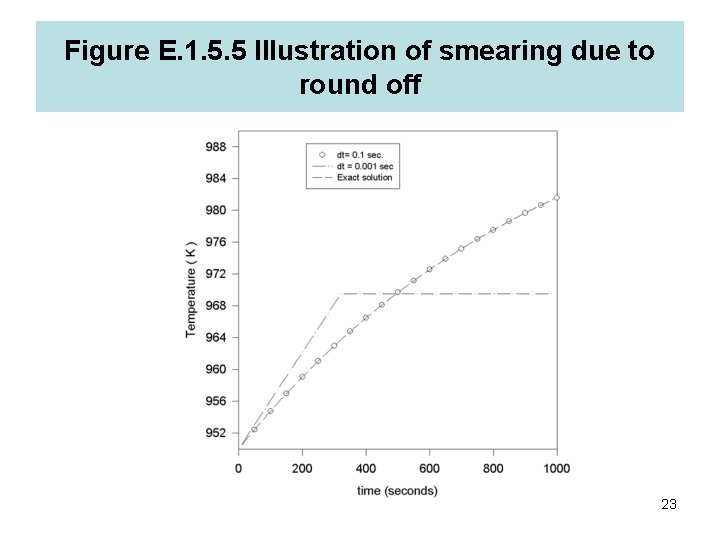
Example E 1. 5. 5 Consider the transient heat equation: d. T/dt = -(Ta - T)/ h where t is the time, h is a characteristic thermal relaxation time, and Ta is the ambient temperature (the temperature of the surroundings). Use a finite difference method to find the variation of the temperature T of an object, initially at a temperature T 0 = 950 K, after it is immersed in a fluid having an uniform temperature Ta = 1000 K: Tnew = Told + t(Ta - Told)/ h where t is the time increment between the old and new temperature and h = 1000 sec. We can start at time t = 0. Set Told = T 0 = 950 and march in time to calculate T at subsequent times. The results with t = 0. 1 and 0. 001 sec are depicted in figure along with the exact solution : T = Ta + (T 0 - Ta)exp(-t/ h) 22

Figure E. 1. 5. 5 Illustration of smearing due to round off 23

Truncation errors are those which usually arise from neglecting (cutting) a number of terms in a series formulation. The geometric series is given by: in the interval -1 < x < 1 for n = 0, 1, 2, 3… when x = 0. 5, the exact value of (x) = 2. If we represent this function by only three terms (n = 2), then: (0. 5) 1 + x 2 = 1 + 0. 5 + (0. 5)2 = 1. 75 Hence, the truncation error T. E. for n = 2, is given by: T. E. = [ (0. 5)exact - (0. 5)approx] = 2 - 1. 75 = 0. 25 = Et = true error or the true relative error, et = Et/2. 0 = 0. 125 (12. 5%) This truncation error is the sum of all the terms left out from the infinite series. (x) = 1/(1 - x) 1 + x 2 + (T. E. )n=2 24

Taylor series expansion & approximation • • Taylor series is used in Analysis to derive: Integration formulas, functional approximations, finite difference schemes and error analysis A convergent series is a series whose sequence of partial sums converges to a finite sum. A divergent series is a series that does not converge. The geometric series converges for -1< x < 1. As an example let us calculate f(x=0. 1): n=0 S 0=1 =1. 000 n=1 S 1=1 + x 2 =1. 100 n=2 S 2=1 + x 2 =1. 110 n=∞ S∞=1. 0/(1 -0. 1) =1. 111111…… 25

Determining of converges • To determine whether a series is convergent or not, there are two most commonly applied tests: • The nth term test states that the series: Sum=q 1+q 2+q 3+…+qn • Converges if qn approaches zero in the limit of the nth term must go to zero as n approaches ∞. • According to the ratio test, if a series with the sequence of the summation of its term q 1, q 2, q 3, …. qn has the property that. • If R<1 or R=0, the series converges absolutely. • If R>1, the series diverges. • If R=1, the series may or may not converge. 26

Example E. 1. 6. 1 27

Approximation of Functions: Taylor Series Taylor's Theorem (Taylor`s Formula) Let (x) be a function defined and continuously differentiable in the closed interval from a to x, and it has continuous derivatives of all orders in the same interval. One can then express that function in terms of a power series as follows: (x) = (a) + (1)(a)(x-a) + (2)(a)(x-a)2/2! + (3)(a)(x-a)3/3! + … where (n)(a) denotes the nth order derivative of with respect to the independent variable x, then, evaluated at the point x = a. The point x = a about which the expansion is built is known as the base point. If the Taylor series is truncated after a finite number of terms, then the sum of all the terms truncated is called the remainder Rn(x). That is: (x) = (a) + (1)(a)(x-a) + (2)(a)(x-a)2/2! + (3)(a)(x-a)3/3! +. . . + (n)(a)(x-a)n/n! + Rn(x) 28

Taylor Series The remainder Rn(x) can be written (Stein, 1967) in the integral form as: where t is a dummy variable used for the purpose of integration. Using the first and second mean value theorems of calculus for integrals, Eq. 1. 6. 5 can be written as: 29

Taylor Series (Cont’d) Different forms of the Taylor series In Taylor`s Theorem, let a = xi (meaning the ith point) and let x = xi+1 = a+h = xi+h denote the next point. Then it takes the form: (xi+1) = (xi) + (1)(xi)h + (2)(xi)h 2/2! + (3)(xi)h 3/3! + … + (n)(xi)hn/n! This form is particularly convenient for developing finite difference formulae. This equation can be further simplified with a change of notation: i = (xi); i+1 = (xi+1); i(n) = (n)(xi) Hence, we can write: i+1 = i + i(1)h + i(2)h 2/2! + i(3)h 3/3! + … + i(n)hn/n! +. . . This form is convenient in deriving formulae for the integration of ordinary differential equations (see Chapter 6). Some simple formulae for computing the derivative of a function numerically are given here as an introduction to numerical differentiation. 30

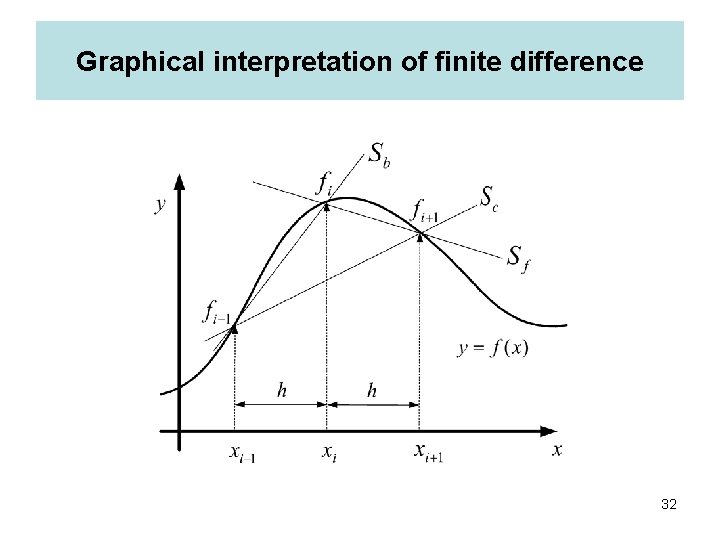
Numerical differentiation We truncate the Taylor series after the second term and solve for (1) = to obtain: = ( i+1 - i)/h or ; Forward Difference where h = xi+1 -xi = x. This is called a first order, forward difference approximation for the first derivative at the point x = xi = a. Note that the fundamental definition of the derivative of a function is: Hence, Sf should become more and more accurate as we make the step size h smaller and smaller. However, one must be careful with round off errors Other formulae can also be derived with the help of Taylor series expansion. (see fig. below) ; Backward difference ; Central difference 31

Graphical interpretation of finite difference 32

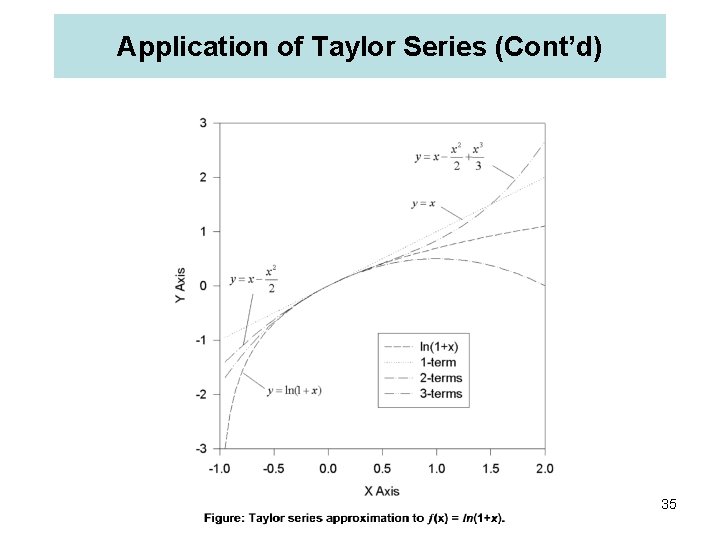
Application of Taylor Series Example: Using Taylor series, expand the function (x) = ln(1+x) about the base point a = 0. Also, using Taylor's formula, approximate this function as a first, second, and third degree polynomial. Compute ln(1. 5) from the Taylor series with increasing an number of terms and make a table of the true and approximate errors as a function of the number of terms used in the summation. Further, estimate the truncation error. Solution: (x) = ln(1+x) (1)(x) = 1/(1+x) (2)(x) = -1/(1+x)2 (3)(x) = (2)(1)/(1+x)3 (4)(x) = -(3)(2)(1)/(1+x)4. . (n)(x) = (-1)n+1(n-1)!/(1+x)n a = 0; (0) = 0, (1)(0) = 1, (2)(0) = -1, (3)(0) = 2, (4)(0) = -6 Substituting all of this into Eq. 1. 6. 4 yields: (x) = ln(1+x) = 0 + x - x 2/2 + x 3/3 - x 4/4 +. . . + (-1)n-1 xn/n +. . To determine for what values of x this series is convergent, apply the ratio test: 33 Hence, the series is convergent in the interval -1 < x < 1.

Application of Taylor Series (Cont’d) Polynomial approximation (truncate Taylor series with finite terms) One term Two terms Three terms ln(1+x) x - x 2/2 + x 3/3 (straight line) (parabola) (cubic polynomial) These approximate functions are plotted in the figure below in comparison with the original function, (x) = ln(1+x). It is seen that as we take more and more terms, the approximate function (polynomial) represents the original function better and better in the neighborhood of the base point x = a = 0. 34

Application of Taylor Series (Cont’d) 35

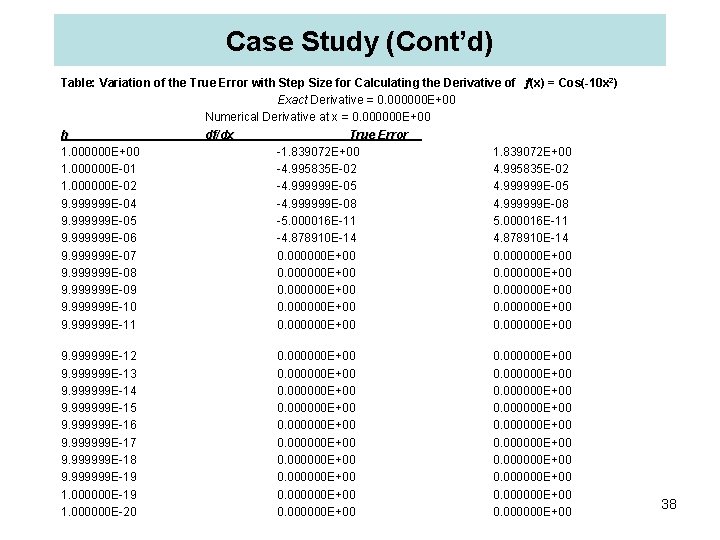
Case Study C 1. 7. 1 Numerical Evaluation of Derivatives Using the approximate forward difference formula for the derivative of a function, calculate numerically the derivatives of the following functions at the specified points. Make a table for each case showing the variation of the exact derivative, the numerical derivative, and the absolute true error with the step size h. Let h vary between 1. 0 and 1. E-20 decreasing each time by a factor of 10 times. (a. ) (x) = Cos(-10 x 2) at x = 0 (b. ) (x) = e-ln(1/x) at x = 1. 0 (c. ) (x) = x/(5+3 x-5) at x = 10 Note: (x 0) [ (x 0 +h) - (x 0)]/h. 36

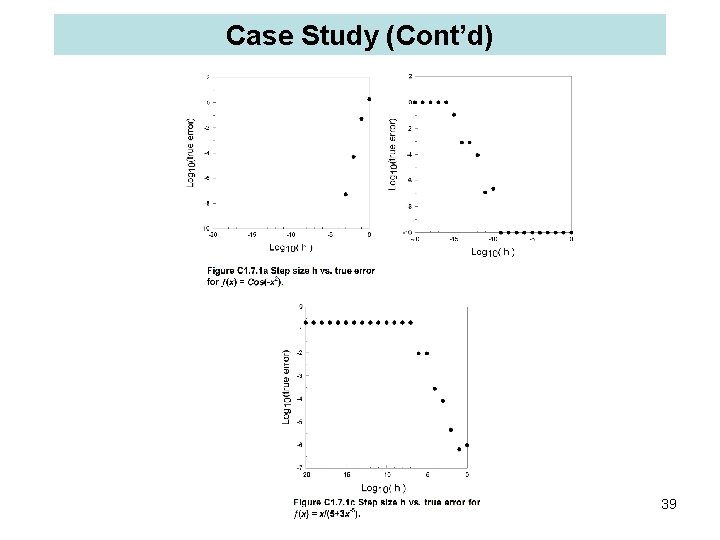
Case Study (Cont’d) Let us first determine analytical derivatives: (a) '(x) = 20 x. Sin(-10 x); '(0) = 0. (b) '(x) = [e-ln(1/x)]/x = 1 ; '(1) = 1. 0 (c) '(x) = (5 + 18 x-5)/(5 + 3 x-5)2 ; '(10) = 0. 2000048 Numerical results for parts (a. ), (b. ), and (c. ) are tabulated in Tables C 1. 7. 1 a-c, and shown in Figures C 1. 7. 1 a-c. For case (b. ), note that (x) = eln(x) = x. Hence, df/dx = 1. 0. We obtain the exact derivative with any value of h that is not very small so that the round off error becomes significant. When h becomes very small, we are adding a small number h to a large number that cannot be handled by the computer. For example, for small h: [ (1 + h) - (1)]/h [ (1) - (1)]/h = 0. 0 (wrong !) 37

Case Study (Cont’d) Table: Variation of the True Error with Step Size for Calculating the Derivative of (x) = Cos(-10 x 2) Exact Derivative = 0. 000000 E+00 Numerical Derivative at x = 0. 000000 E+00 h df/dx True Error 1. 000000 E+00 -1. 839072 E+00 1. 000000 E-01 -4. 995835 E-02 1. 000000 E-02 -4. 999999 E-05 9. 999999 E-04 -4. 999999 E-08 9. 999999 E-05 -5. 000016 E-11 9. 999999 E-06 -4. 878910 E-14 9. 999999 E-07 0. 000000 E+00 9. 999999 E-08 0. 000000 E+00 9. 999999 E-09 0. 000000 E+00 9. 999999 E-10 0. 000000 E+00 9. 999999 E-11 0. 000000 E+00 9. 999999 E-12 9. 999999 E-13 9. 999999 E-14 9. 999999 E-15 9. 999999 E-16 9. 999999 E-17 9. 999999 E-18 9. 999999 E-19 1. 000000 E-20 0. 000000 E+00 0. 000000 E+00 38

Case Study (Cont’d) 39

• End of Chapter 1 40

References • • • Celik, Ismail, B. , “Introductory Numerical Methods for Engineering Applications”, Ararat Books & Publishing, LCC. , Morgantown, 2001 Fausett, Laurene, V. “Numerical Methods, Algorithms and Applications”, Prentice Hall, 2003 by Pearson Education, Inc. , Upper Saddle River, NJ 07458 Rao, Singiresu, S. , “Applied Numerical Methods for Engineers and Scientists, 2002 Prentice Hall, Upper Saddle River, NJ 07458 Mathews, John, H. ; Fink, Kurtis, D. , “Numerical Methods Using MATLAB” Fourth Edition, 2004 Prentice Hall, Upper Saddle River, NJ 07458 Varol, A. , “Sayisal Analiz (Numerical Analysis), in Turkish, Course notes, Firat University, 2001 41