MTH 352 Differential Geometry For Master of Mathematics










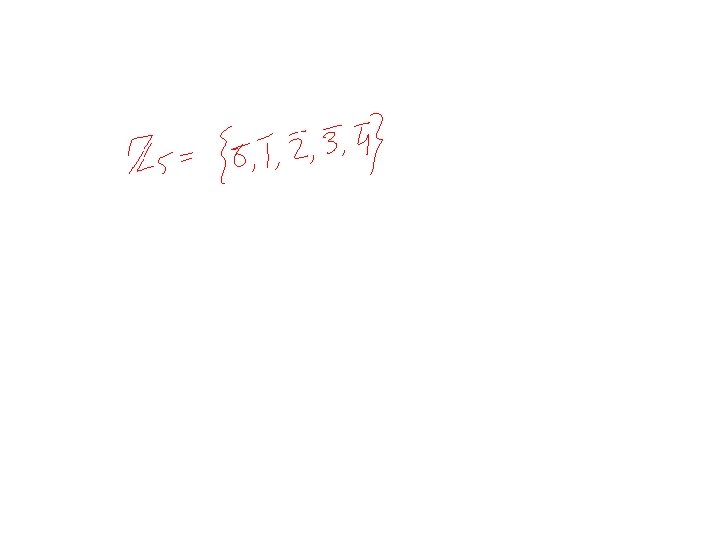

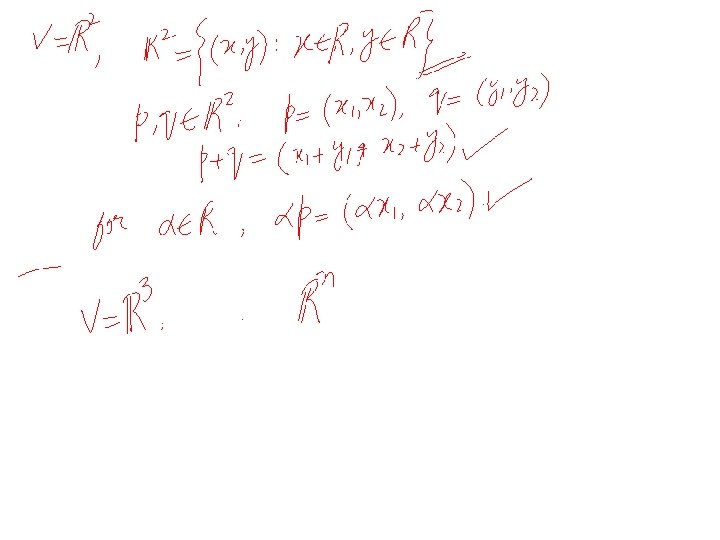




- Slides: 27

MTH 352: Differential Geometry For Master of Mathematics By Dr. SOHAIL IQBAL Assistant Professor Department of Mathematics, CIIT Islamabad 1

Euclid: ØHe is often referred to as the "Father of Geometry“. ØEuclid's Elements. ØHis work is one of the most influential works in the history of mathematics. The “Elements” have been serving as the main textbook for teaching geometry from the 300 B. C. until the 20 th century. Archimedes ØGive me a place to stand on, and I will move the Earth. ØCalculated the area and volumes of different objects, the techniques were later formulated in calculus. 2

Muslim Era: Ø The need to predict the phases of the Moon for Ramadan and other religious festivals led to great steps forward in geometry of celestial objects (astronomy). René Descartes/ Pierre de Fermat Ø Introduction “Cartesian coordinates” which marked a new stage for geometry, since geometric figures, could now be represented analytically, that is, with functions and equations. Ø Built a bridge between algebra and geometry. 3

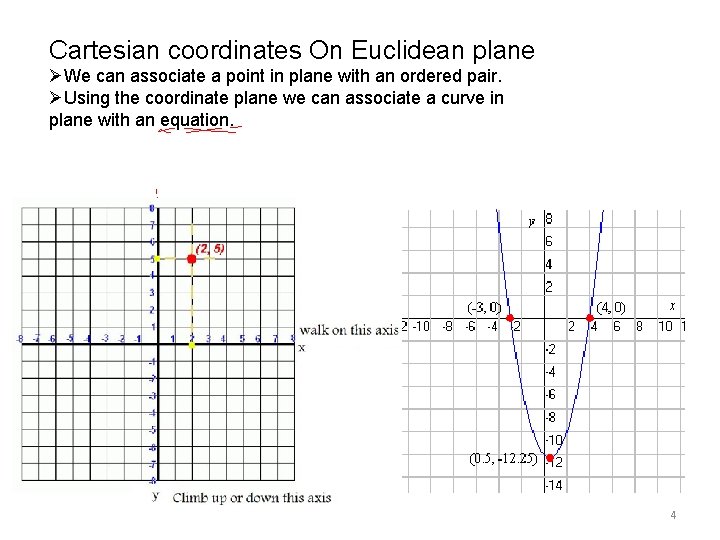
Cartesian coordinates On Euclidean plane ØWe can associate a point in plane with an ordered pair. ØUsing the coordinate plane we can associate a curve in plane with an equation. 4

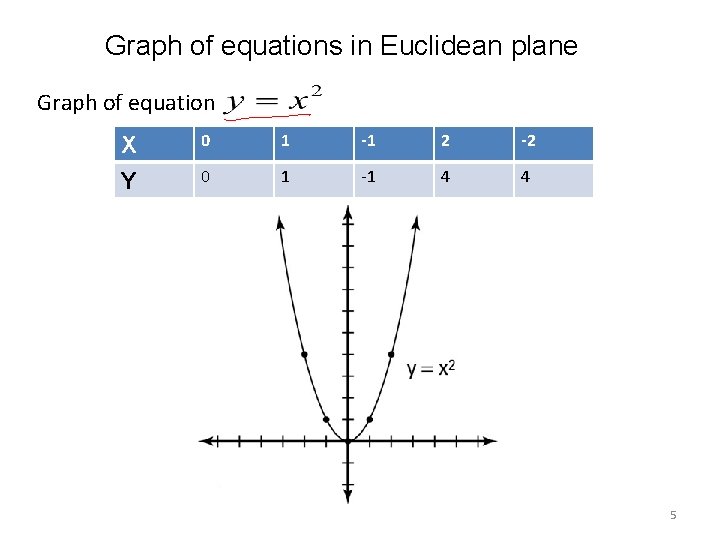
Graph of equations in Euclidean plane Graph of equation X Y 0 1 -1 2 -2 0 1 -1 4 4 5

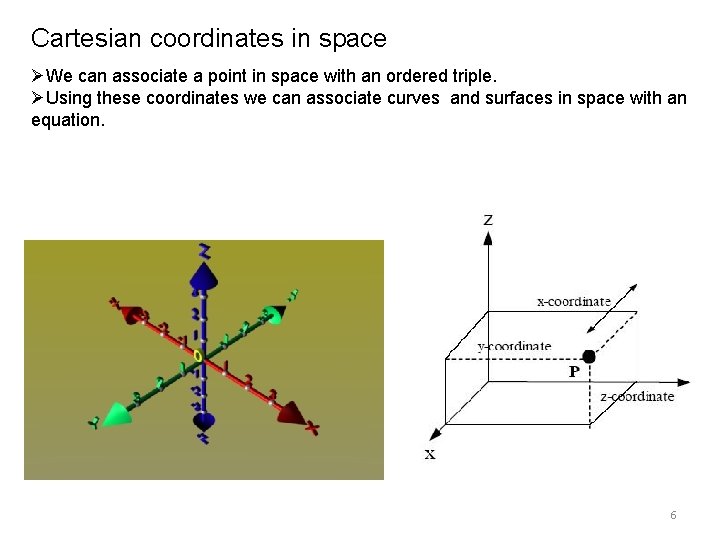
Cartesian coordinates in space ØWe can associate a point in space with an ordered triple. ØUsing these coordinates we can associate curves and surfaces in space with an equation. 6

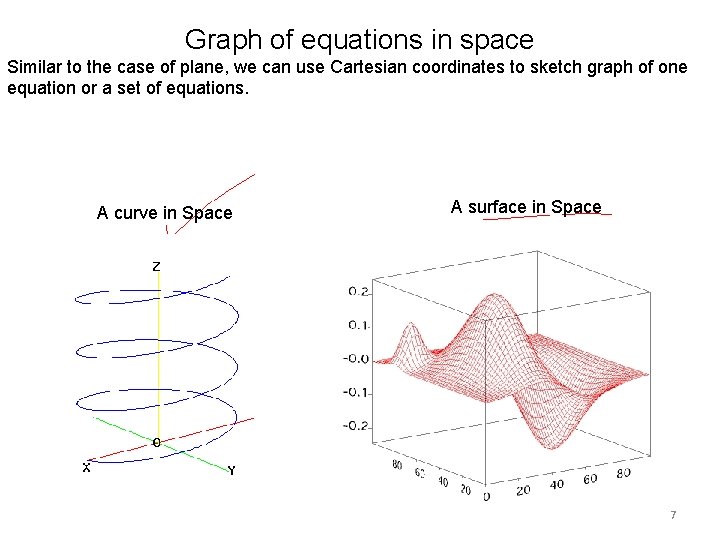
Graph of equations in space Similar to the case of plane, we can use Cartesian coordinates to sketch graph of one equation or a set of equations. A curve in Space A surface in Space 7

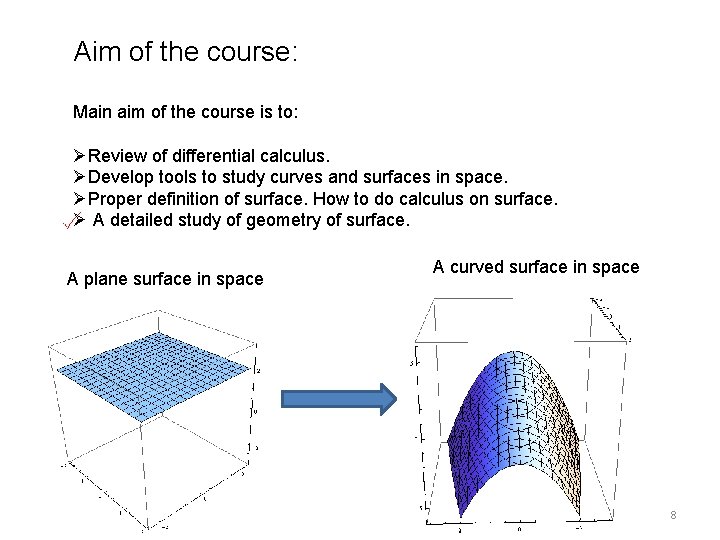
Aim of the course: Main aim of the course is to: ØReview of differential calculus. ØDevelop tools to study curves and surfaces in space. ØProper definition of surface. How to do calculus on surface. Ø A detailed study of geometry of surface. A plane surface in space A curved surface in space 8

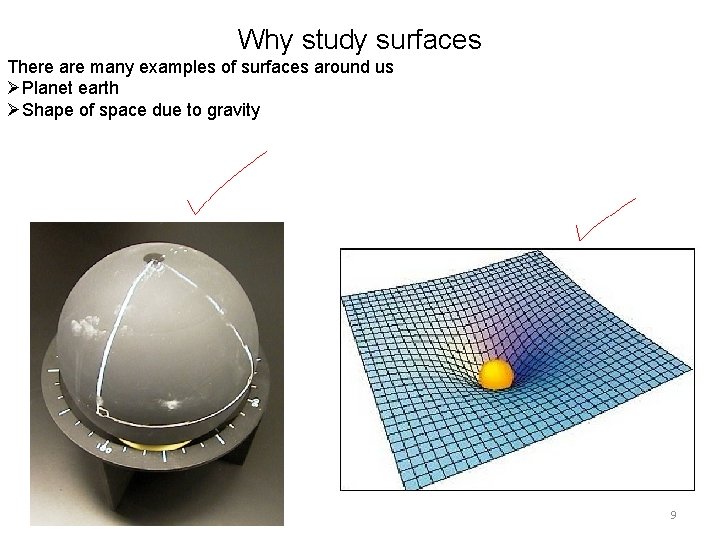
Why study surfaces There are many examples of surfaces around us ØPlanet earth ØShape of space due to gravity 9

Textbook: Author: Barrett O’Neill Title: Elementary Differential Geometry Marks scheme : Quizzes – 10% assignments – 10% GDB – 5% Sessionals(I & II) – 25% Final – 50% 10

SOME DEFINITIONS: Set : A set S is a collection of objects that are called the elements of S. Example 1: S = {1, 2, 3, 4, …} is a set of natural numbers. Example 2: S = { x : x is an integer ^ x is divisible by 2} = Set of even integers. Subset: A set A is a subset of S provided each element of A is also an element of S. Example 1: A = {1, 2, 3} is a subset of S = {1, 2, 3, 4, …}. Example 2: A = { x : x is an integer ^ x is divisible by 2 } is a subset of integers. 11

SOME DEFINITIONS: • 12

SOME DEFINITIONS: • (E) D 13

SOME DEFINITIONS • 14

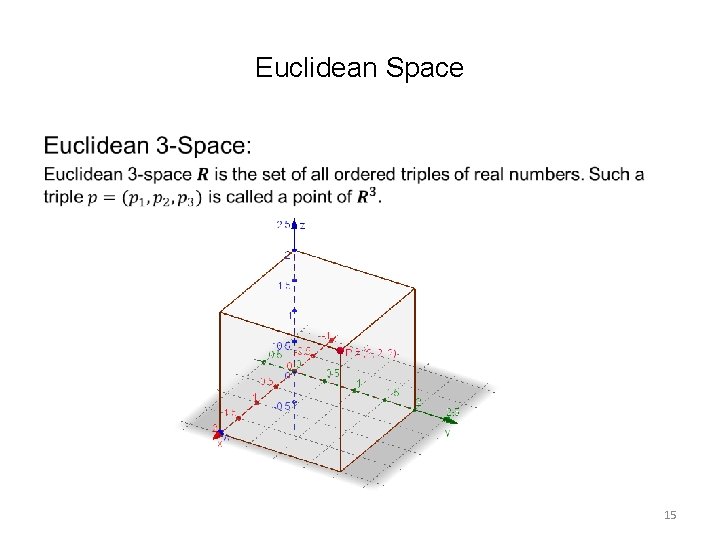
Euclidean Space • 15

Euclidean Space • 16

Field • 17
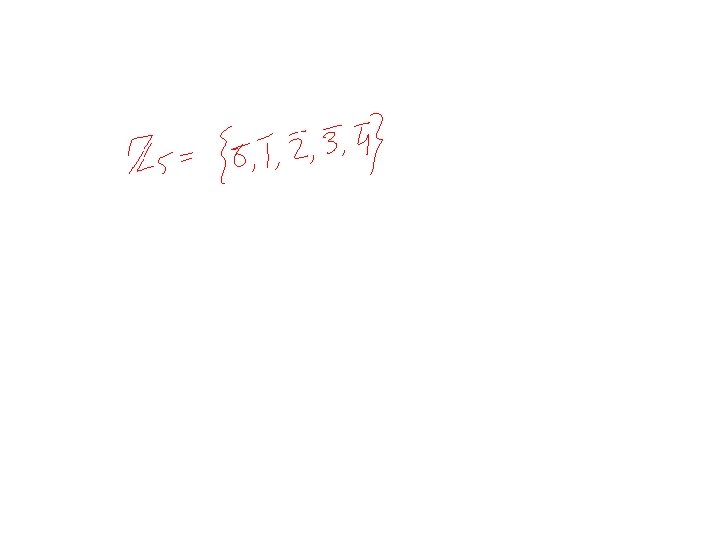

Closed under addition and scalar mult Associativity of addition Commutativity of addition Identity element of addition Inverse elements of addition Distributivity of scalar multiplication with respect to vector addition Distributivity of scalar multiplication with respect to field addition Compatibility of scalar multiplication with field multiplication Identity element of scalar multiplication 19
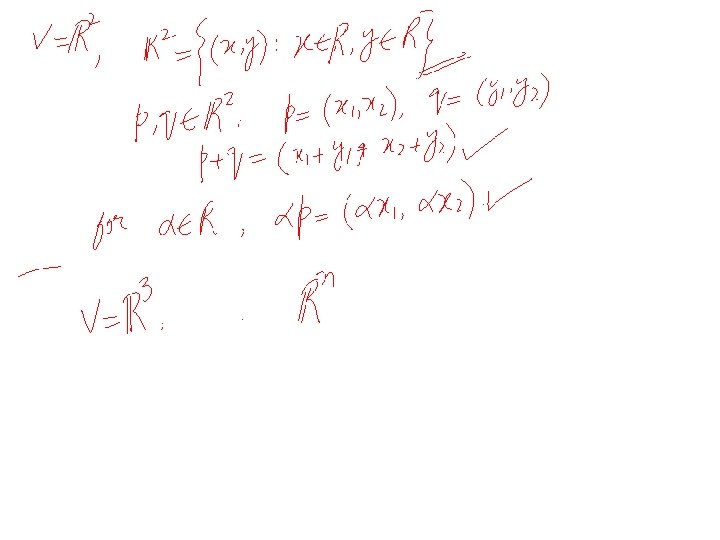

Euclidean Space • 21


Arithmetic of differentiable functions • 23

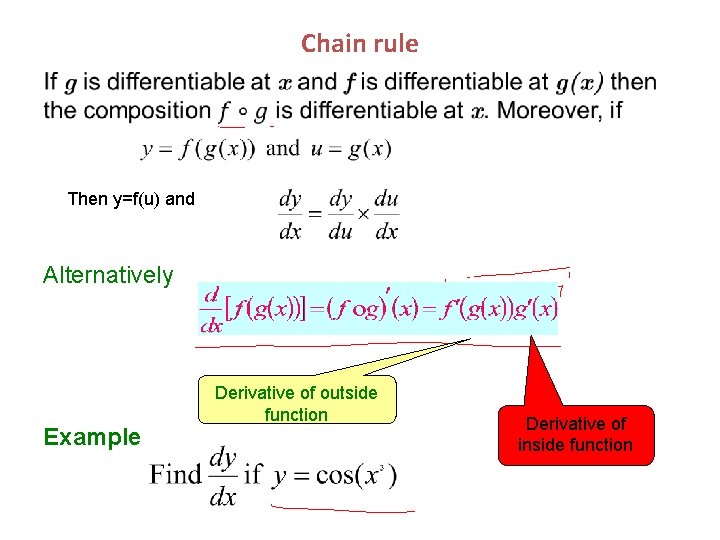
Chain rule Then y=f(u) and Alternatively Example Derivative of outside function Derivative of inside function

Let And Rates of change multiply
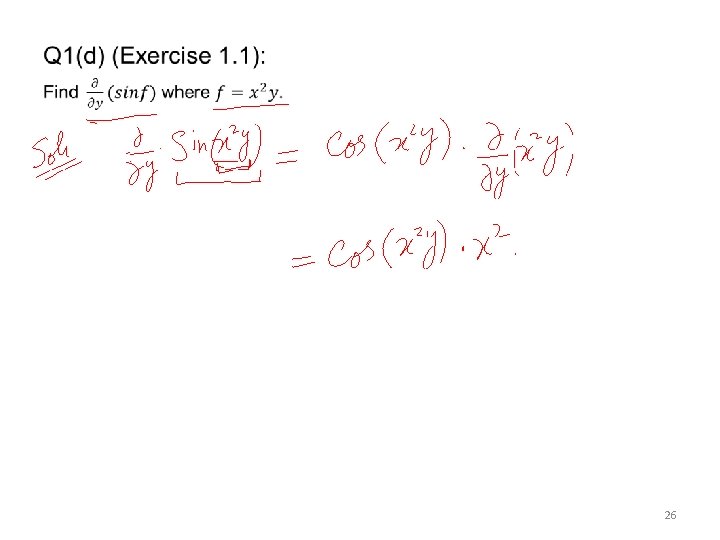
 Mth104
Mth104 Mth 105
Mth 105 Mth 685
Mth 685 Mth
Mth Mth 685
Mth 685 Mth 210
Mth 210 Mth 210
Mth 210 Mth 685
Mth 685 Grade 11 theorems
Grade 11 theorems Visual differential geometry
Visual differential geometry Differential geometry
Differential geometry Differential geometry
Differential geometry 1-form differential geometry
1-form differential geometry Scm 352
Scm 352 Ece 352
Ece 352 Exam feedback examples
Exam feedback examples Opwekking 352
Opwekking 352 Union viga columna hormigon armado
Union viga columna hormigon armado Os 352
Os 352 Os 352
Os 352 One hot state assignment
One hot state assignment Ece352
Ece352 Troop 352
Troop 352 Saumya debray
Saumya debray Os 352
Os 352 352 formação
352 formação It 352
It 352 Tmk 352
Tmk 352